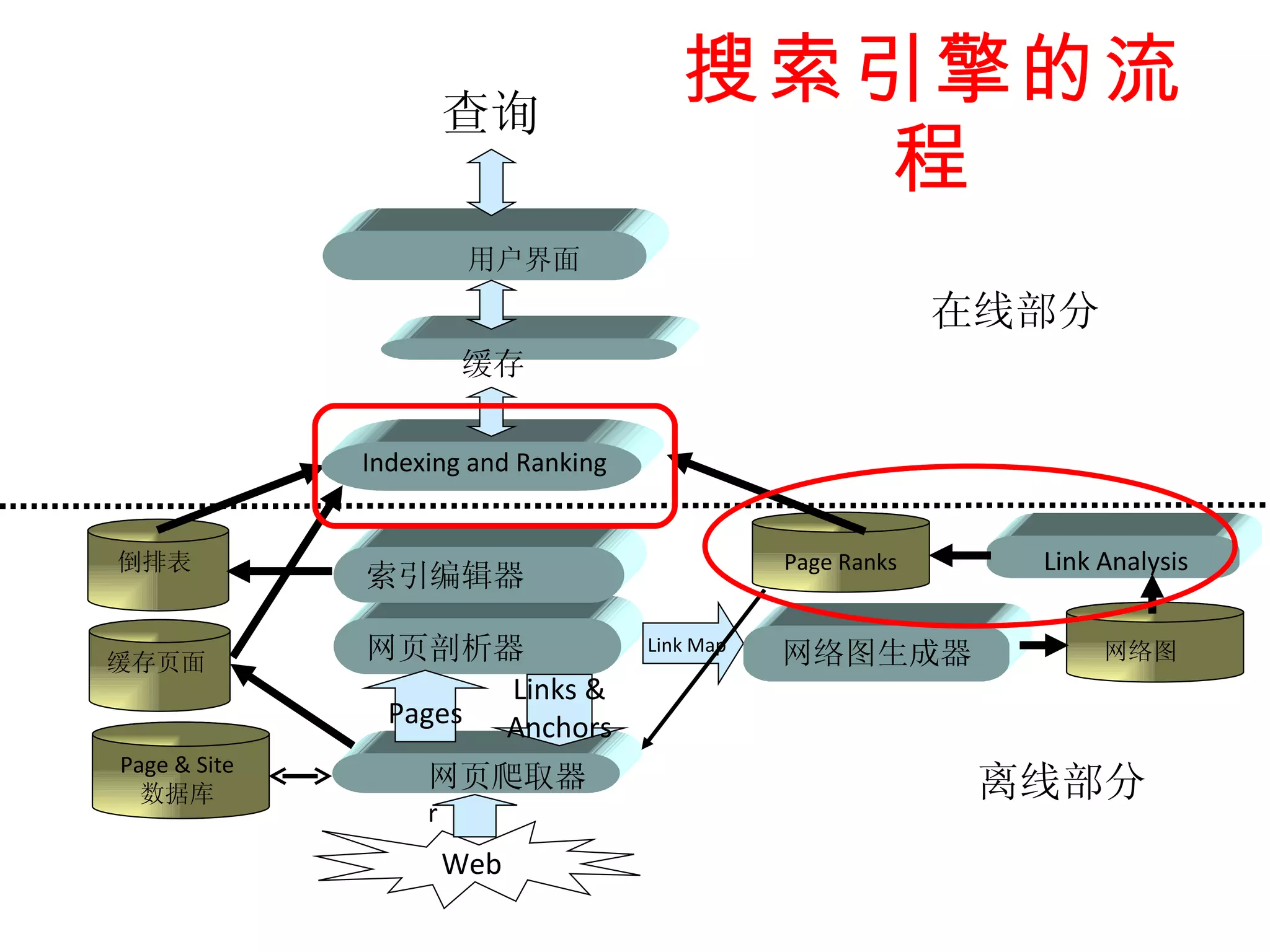
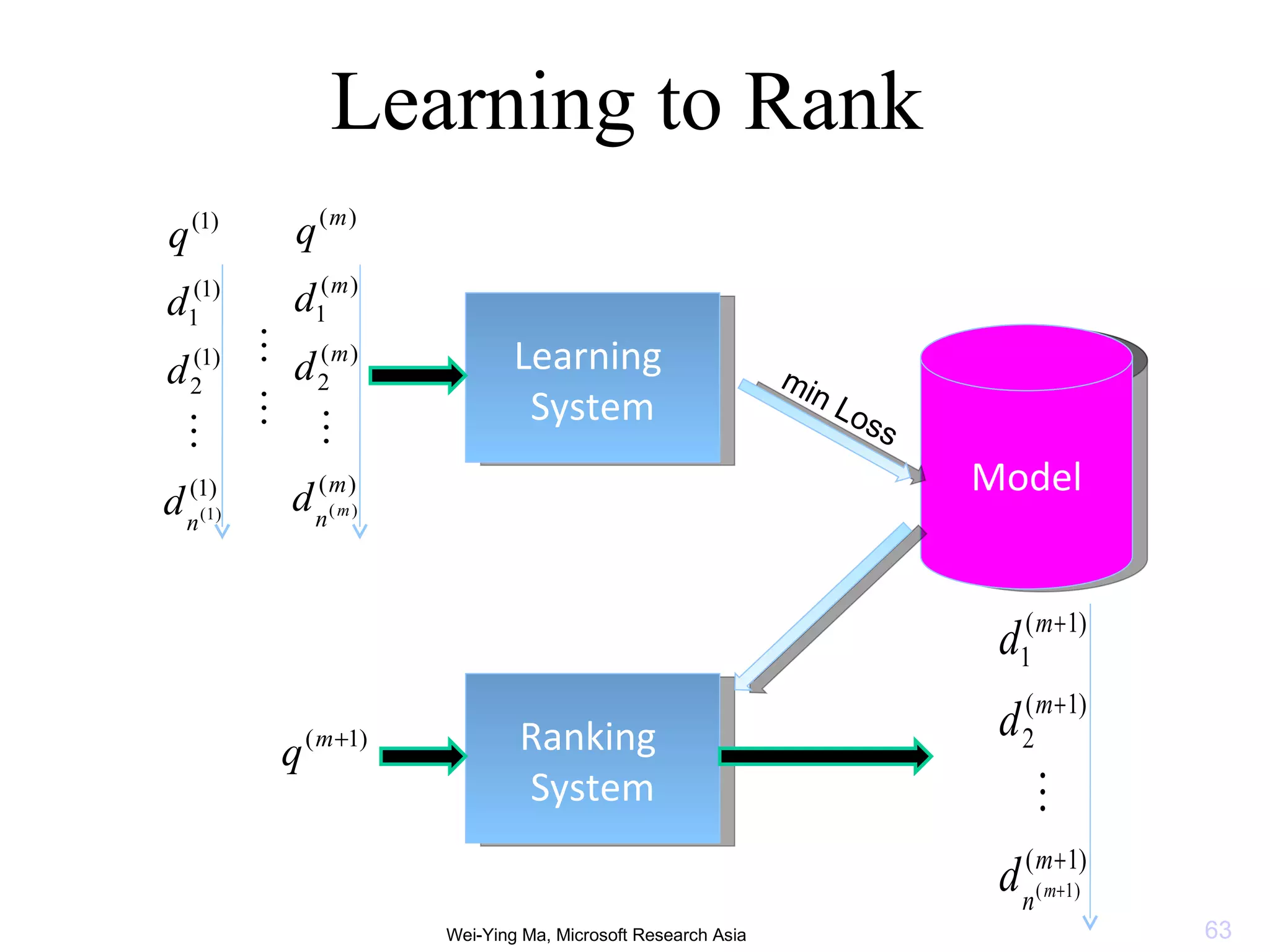
This document discusses several key aspects of mathematics and algorithms used in internet information retrieval and search engines: 1. It explains how search engines like Google can rapidly rank billions of web pages using algorithms based on the topology and link structure of the web graph, such as PageRank. 2. It describes two main types of page ranking algorithms - static importance ranking based on link analysis, and dynamic relevance ranking based on statistical learning models to match pages to queries. 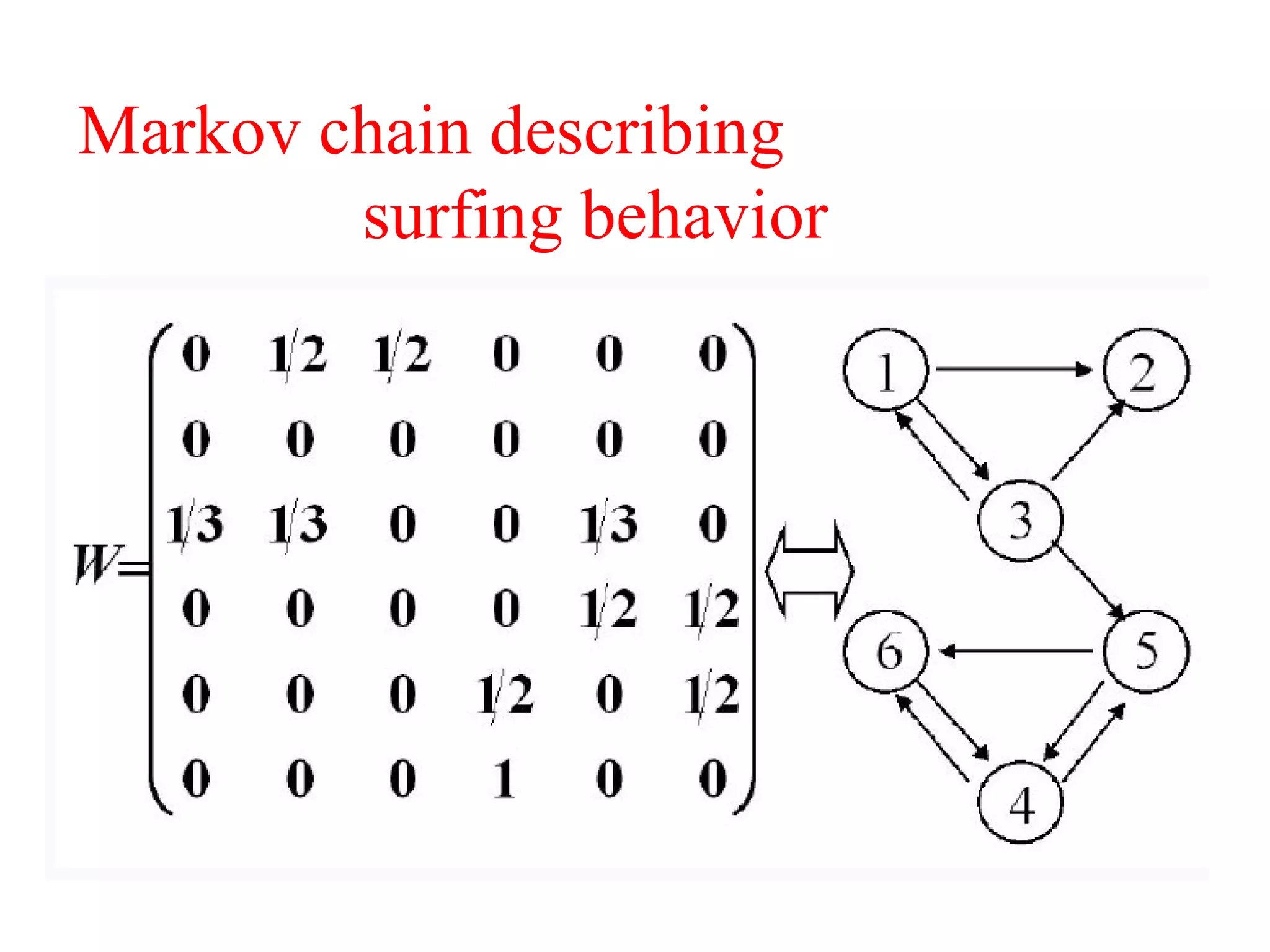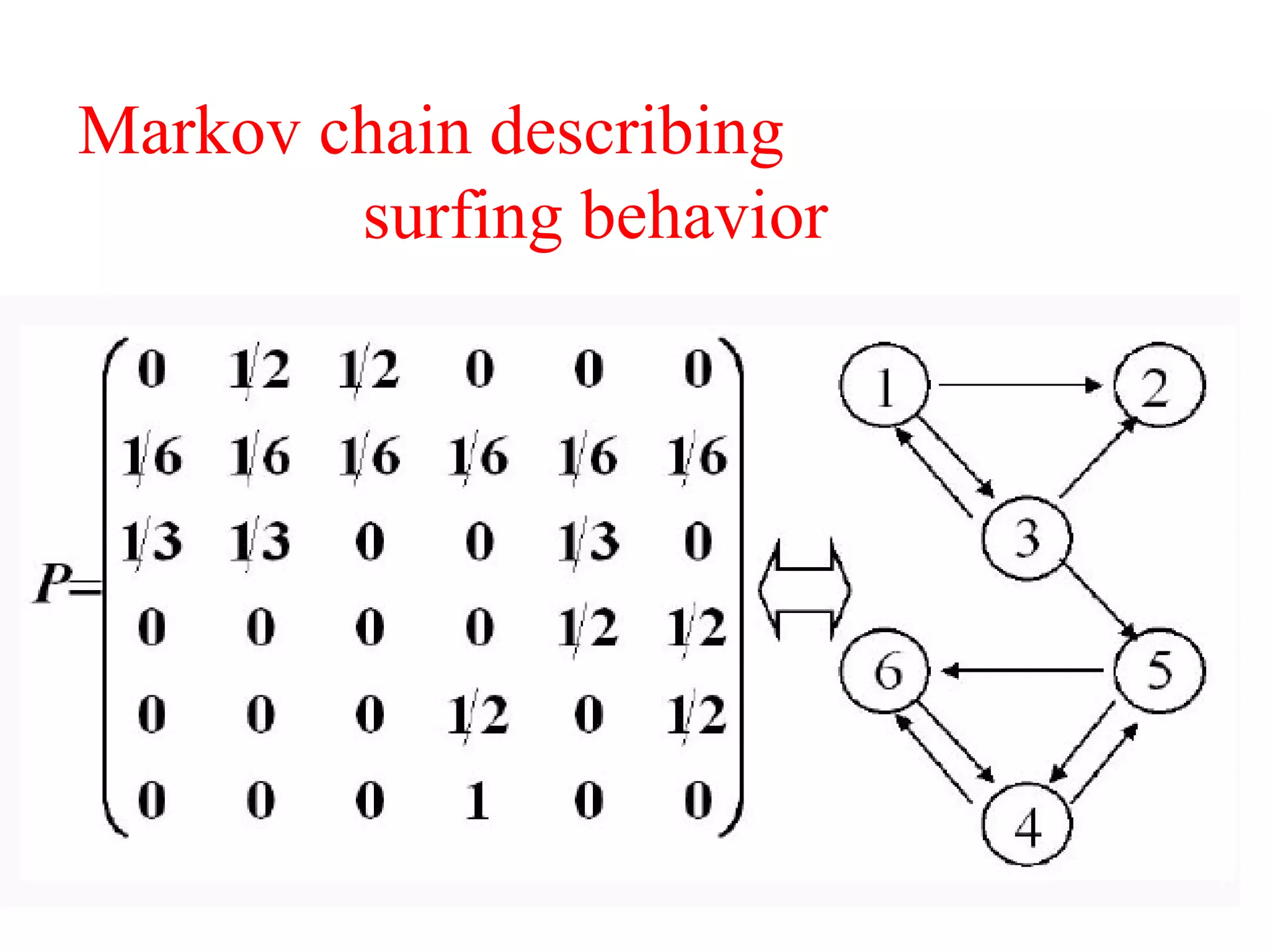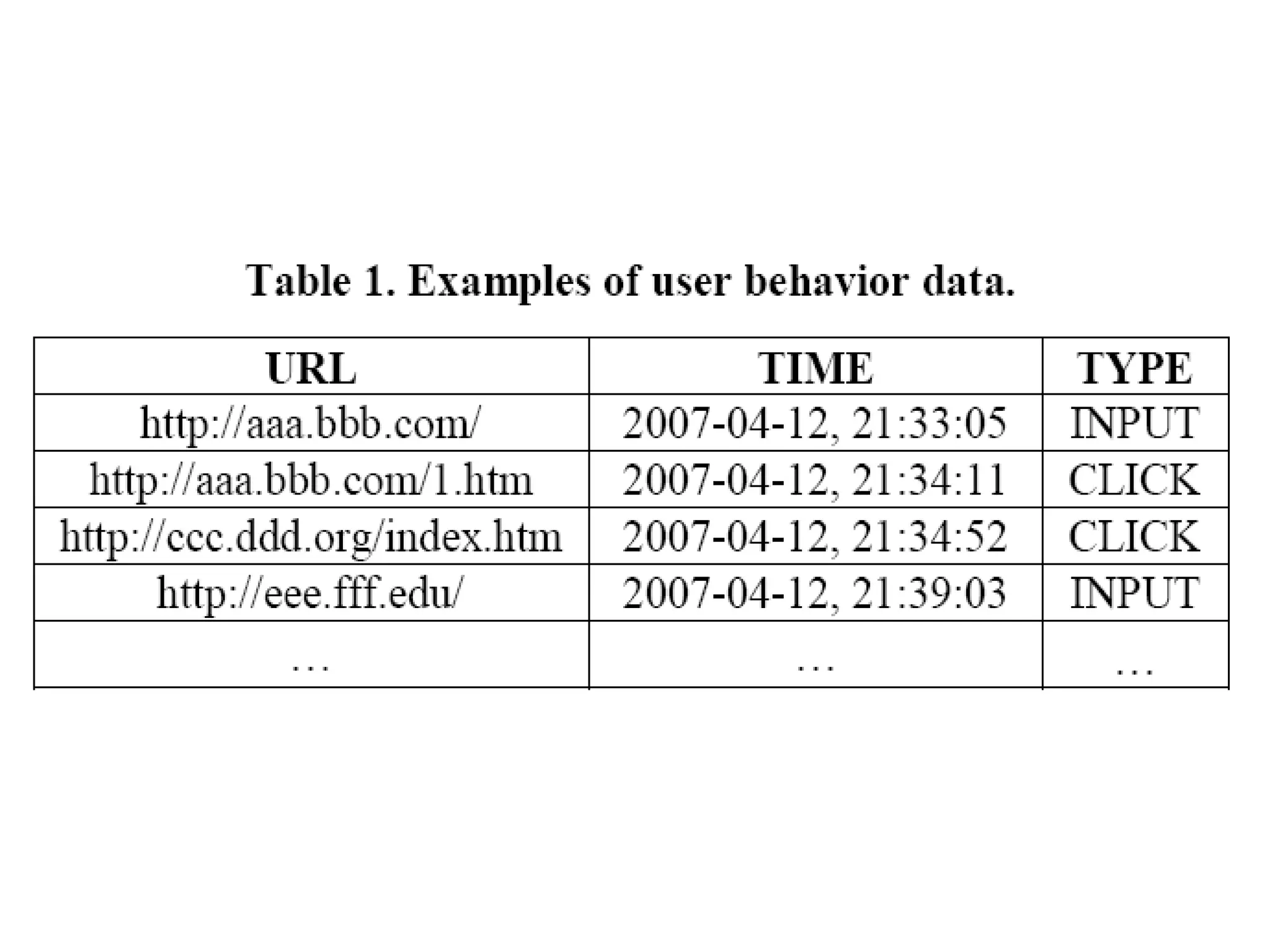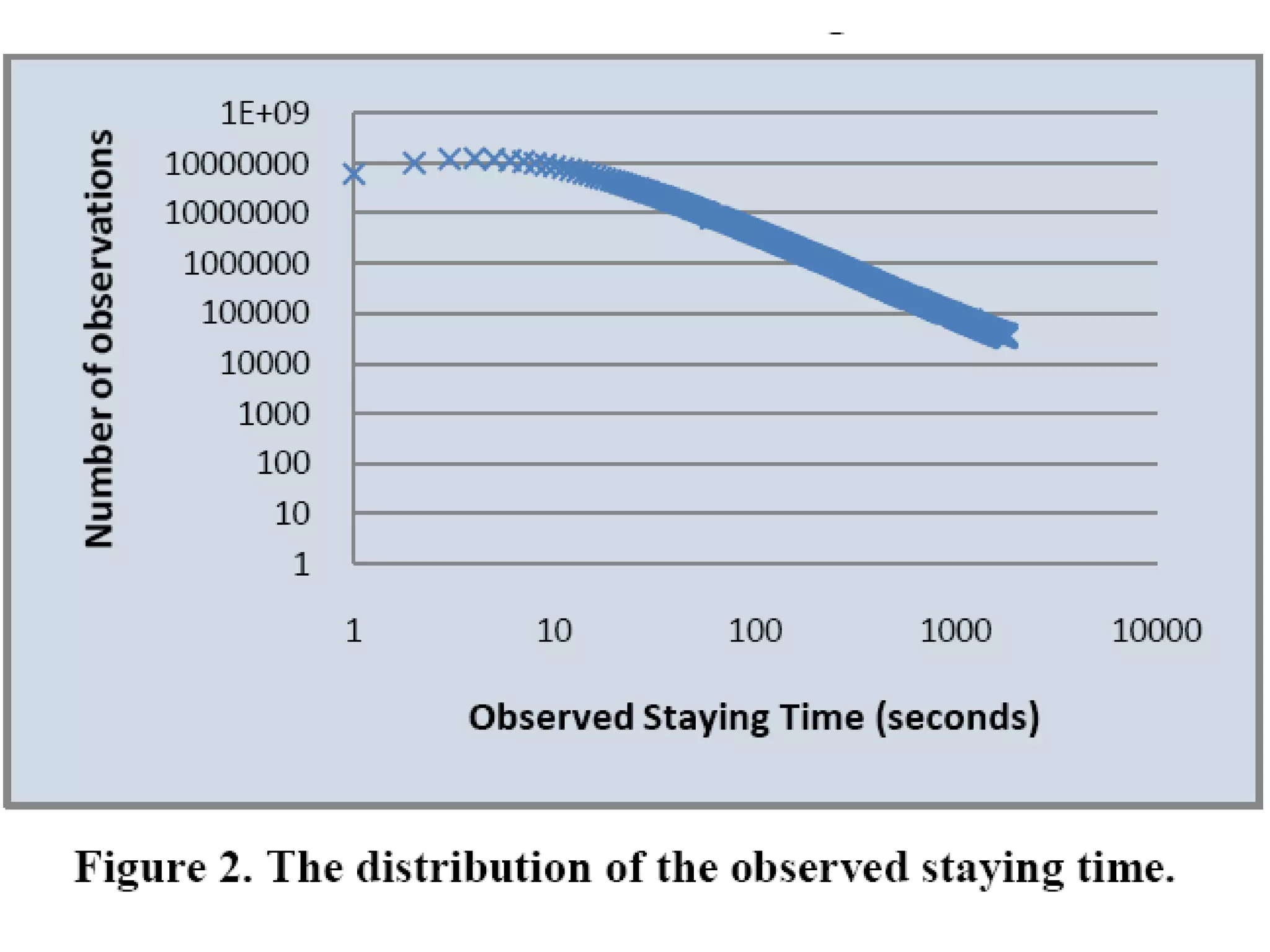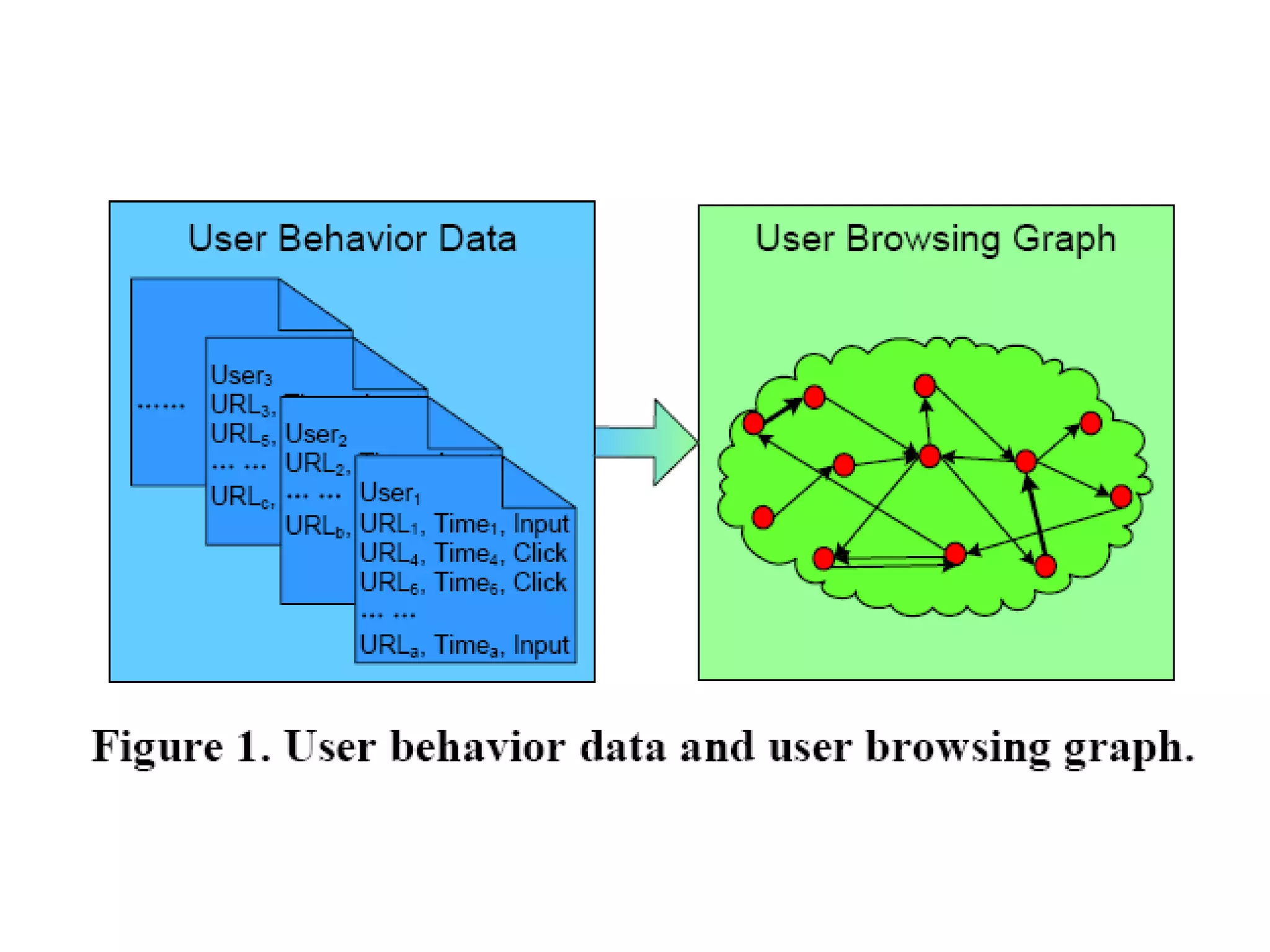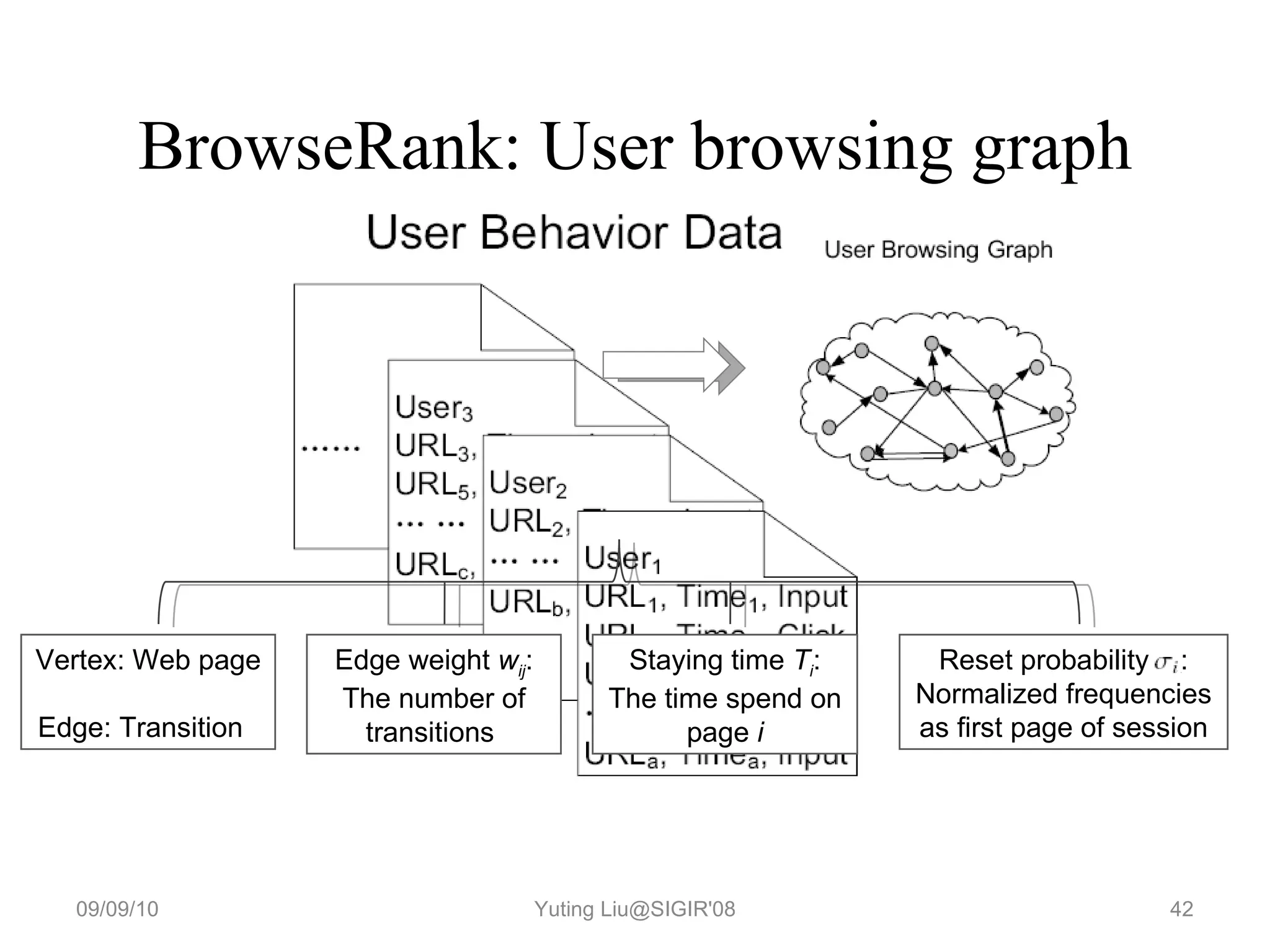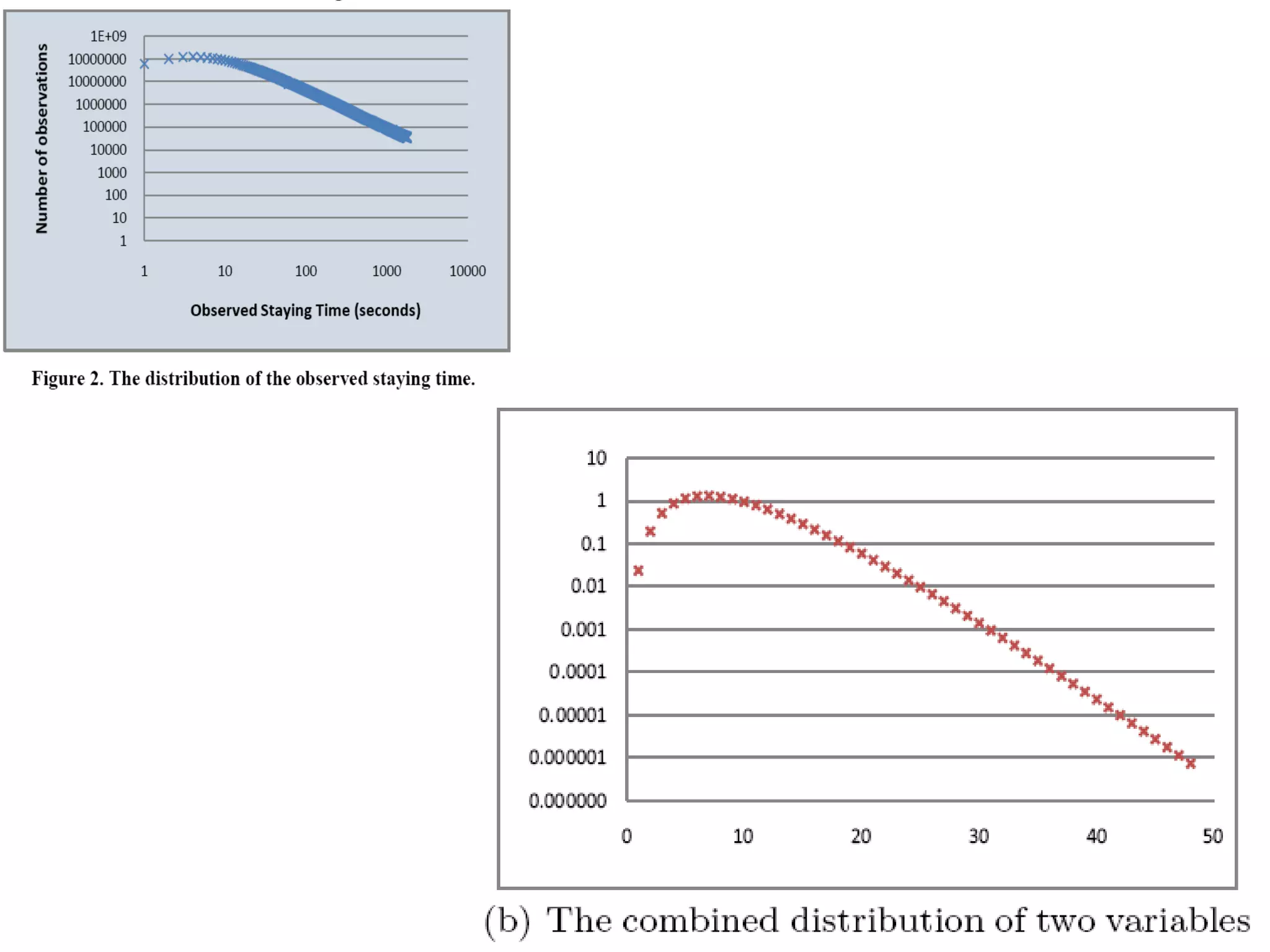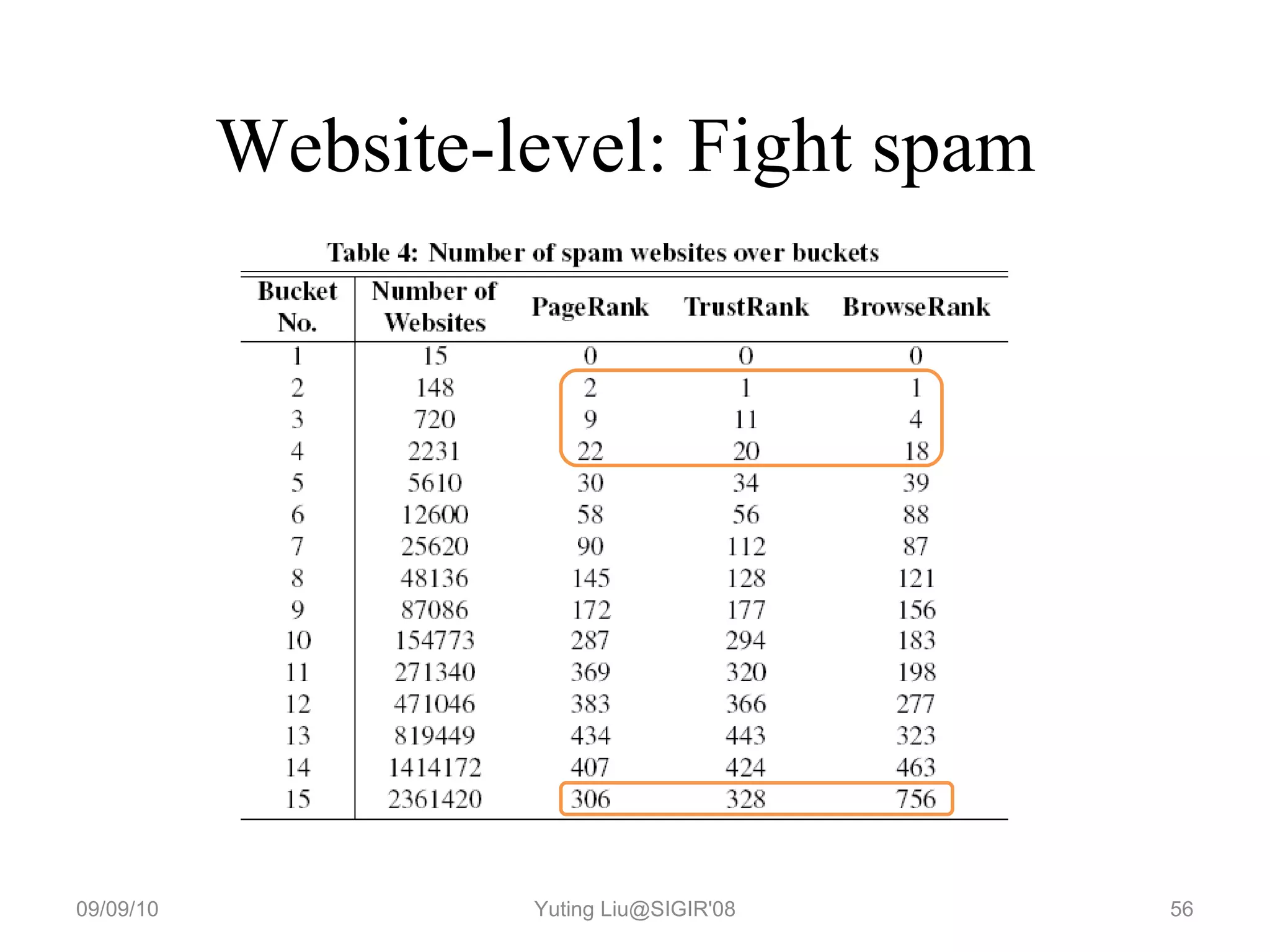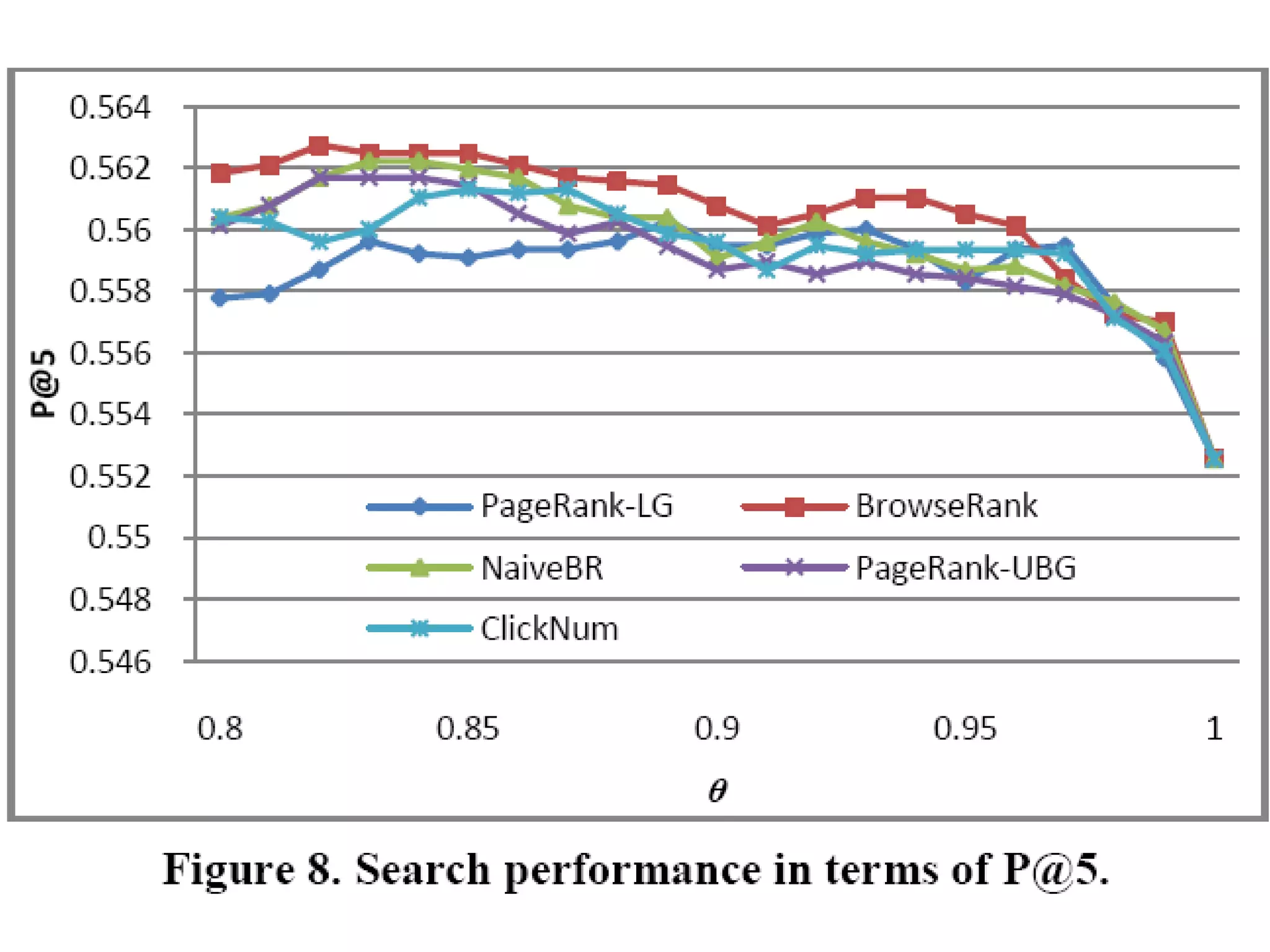3. It proposes a new ranking algorithm called BrowseRank that models user browsing behavior using Markov chains and takes into account visit duration to better reflect true page importance.

1. Internet 信息检索中的数学 Zhi-Ming Ma April 24, 2009, 厦门 Email: mazm@amt.ac.cn http://www.amt.ac.cn/member/mazhiming/index.html

3. How can google make a ranking of 2,040,000 pages in 0.11 seconds?

4. A main task of Internet (Web) Information Retrieval = Design and Analysis of Search Engine (SE) Algorithm involving plenty of Mathematics

5. Inter network is a large scale complex random network The Earth is developing an electronic nervous system, a network with diverse nodes and links are

6. 搜索引擎的流程 Web Links & Anchors Pages Link Map 查询 在线部分 离线部分 Link Analysis 缓存 网页剖析器 倒排表 Page & Site 数据库 网络图 网页爬取器 r 用户界面 缓存页面 索引编辑器 Page Ranks 网络图生成器 Indexing and Ranking

7. Static Rank ( 静态排序） Importance ranking Goal: compute page importance, page authority Method: Link analysis A method is based on the topology of the graph of whole Web pages. Web graph: page  node, hyperlink  edge. Algorithms: HITS(Kleinberg) [5] PageRank(GOOGLE) [6]

8. Dynamic Rank （动态排序） Relevance ranking （相关性排序） Goal: compute the content match relevant score between pages and query. Method: Statistic machine learning Algorithms: Point-wise: BM25[7] Pair-wise: RankBoost[3], RankSVM[4], RankNet[1],… List-wise: ListNet[10]

9. Research on Complex Networks and Information Retrieval In recent years we have been involved in the research direction of Random Complex Networks and Information Retrieval. I shall briefly review some of our recent results ( in collaboration with Microsoft Research Asia ) in this direction.

12. Outlines Markov chain methods in search engines Point process describing Browsing behavior Two layer statistical learning Stochstic complement method in ranking Web sites Final remarks

18. Browse Rank  vs. Page Rank ?

19.  HITS  PageRank 1998 Jon Kleinberg Cornell University Sergey Brin and Larry Page Stanford University

20. Nevanlinna Prize （ 2006) Jon Kleinberg One of Kleinberg‘s most important research achievements focuses on the internetwork structure of the World Wide Web. Prior to Kleinberg‘s work, search engines focused only on the content of web pages ， not on the link structure. Kleinberg introduced the idea of “ authorities” and “hubs”: An authority is a web page that contains information on a particular topic, and a hub is a page that contains links to many authorities. Zhuzihu thesis.pdf

21. Page Rank , the ranking system used by the Google search engine. Query independent content independent. using only the web graph structure

23. Markov chain describing surfing behavior

24. Markov chain describing surfing behavior

25. Web surfers usually have two basic ways to access web pages: with probability α, they visit a web page by clicking a hyperlink. 2. with probability 1-α, they visit a web page by inputting its URL address.

26. where

27. More generally we may consider personalized d .: PageRank is the unique positive eigenvector: By the strong ergodic theorem:

28. Problem:

31. PageRank as a Function of the Damping Factor Paolo Boldi Massimo Santini Sebastiano Vigna DSI, Università degli Studi di Milano WWW 2005 paper 3.1 Choosing the damping factor 3 General Behaviour 3.2 Getting close to 1 can we somehow characterise the properties of ? what makes different from the other (infinitely many, if P is reducible) limit distributions of P ?

32. is the limit distribution of P when the starting distribution is uniform, that is, Conjecture 1 :

33. Research results by our group: Limit of PageRank Comparison of Different Irreducible Markov Chains N-step PageRank ……

34. Weak points of PageRank Using only static web graph structure Reflecting only the will of web managers, but ignore the will of users e.g. the staying time of users on a web. Can not effectively against spam and junk pages. BrowseRankSIGIR.ppt

36. Letting Web Users Vote for Page Importance When calculating the page importance, Use the users’ real browsing behavior Make no artificial assumption on the users’ behavior Use the users’ complete browsing behavior Contain the time information 09/09/10 Yuting Liu@SIGIR'08

38. Browsing Process Markov property Time-homogeneity

42. BrowseRank: User browsing graph 09/09/10 Yuting Liu@SIGIR'08 Vertex: Web page Edge: Transition Edge weight w ij : The number of transitions Staying time T i : The time spend on page i Reset probability : Normalized frequencies as first page of session

43. Mathematical Deduction Maximum likelihood estimation: of staying time

44. Mathematical Deduction where Therefore

45. Mathematical Deduction Additional Noise: the speed of the Internet connection, the length of the page, the layout of the page, user does some other things (e.g.,answers a phone call) Other factors

46. Mathematical Deduction Assume Noise: Chi-square distribution with degree k

47. Mathematical Deduction ideally we would have: However, due to data sparseness, we encounter challenges……

48. Mathematical Deduction To tackle this challenge, we turn it into optimization problems :

50. Mathematical Deduction Stationary distribution: is the mean of the staying time on page i. The more important a page is, the longer staying time on it is. is the mean of the first re-visit time at page i. The more important a page is, the smaller the re-visit time is, and the larger the visit frequency is.

51. Mathematical Deduction Properties of Q process: Jumping probability is conditionally independent from jumping time: Embedded Markov chain: is a Markov chain with the transition probability matrix

52. Mathematical Deduction is the stationary distribution of The stationary distribution of discrete model is easy to compute Power method for Log data for

54. Experiments Data set: 5.6 million vertices 53 million edges Baselines: PageRank, TrustRank Aim to: Find good websites Fight spam websites 09/09/10 Yuting Liu@SIGIR'08

55. Website-level: Find good 09/09/10 Yuting Liu@SIGIR'08

56. Website-level: Fight spam 09/09/10 Yuting Liu@SIGIR'08

58. BrowseRank: Letting Web Users Vote for Page Importance Yuting Liu , Bin Gao, Tie-Yan Liu, Ying Zhang, Zhiming Ma, Shuyuan He, and Hang Li July 23, 2008, Singapore the 31st Annual International ACM SIGIR Conference on Research & Development on Information Retrieval. Best student paper !

59. BrowseRank: Letting Web Users Vote for Page Importance Google search , 110,000,000 results for Browse Rank

60. Further Studies Browsing Processes will be a Basic Mathematical Tool in Internet Information Retrieval How about inhomogenous process? Marked point process Hyperlink is not reliable. Users’ real behavior should be considered.

61. Dynamic Rank （动态排序） Relevance ranking （相关性排序） Goal: compute the content match relevant score between pages and query. Method: Statistic machine learning Algorithms: Point-wise: BM25[7] Pair-wise: RankBoost[3], RankSVM[4], RankNet[1],… List-wise: ListNet[10]

62. Outlines Markov chain methods in search engines Point process describing Browsing behavior Two layer statistical learning Stochstic complement method in ranking Web sites Final remarks

63. Learning to Rank Model Learning System Ranking System Wei-Ying Ma, Microsoft Research Asia min Loss

64. learning to rank in IR is a two layer statistical learning Distributions of the relevance judgments of documents may vary from query to query The numbers of documents for different queries may differ largely Evaluation in IR is usually conducted at query level

65. Document level vs Query level Two queries in total. Same errors in terms of pairwise classification. 780/790=98.73% Different errors in terms of query-level evaluation. 99% vs. 50%.

66. Query-Level Stability and Generalization in Learning to Rank, to appear in Proceedings of the 25th International Conference on Machine Learning 2008, Yanyan Lan, Tie-Yan Liu, Tao Qin, Zhiming Ma, Hang Li Two Layer Statistical Learning and Applications in Information Retrieval, in preparation , Yanyan Lan, Hang Li, Tie-Yan Liu, Zhi-Ming Ma, Tao Qin Microsoft Scholar Fellowship

67. We propose a new framework of statistical learning model, in which the training dada are composed in two layers . the two layer structure of training data is not artificial , but arises from the real world Especially from learning to rank in Information Retrieval

68. Two-Layer Statistical Learning Framework First layer: objects Second layer: associated samples : instances : descriptions of instances Instances are the objectives which we are concern

69. In learning to rank for IR, an object is a query, an instance and corresponding description can be interpreted as a single document ( pointwise algorithm ) a pair of document ( pairwise algorithm ) a set of documents ( listwise algorithm ) a score (or label) of a document an order on a pair of documents a permutation (list) of documents

70. Training Process i.i.d. For each i, the associated samples , distribution the training data is denoted as

71. The algorithm of a training process is to learn from the training data a function that will be used to predict the features of instances.

72. empirical object level loss loss function on expected object level loss

73. empirical risk expected risk

74. The challenge is that when dealing with two layer training data, most of the existing results of statistical learning can not be directly applied. Thus we have to develop new results or modify the existing results to suit the new model. In this aspect much research should be conducted.

75. Generalization Analysis based on Stability Theory Devroye, L. and Wagner, T.(1979). Stability stability-bounds depend on properties of the algorithm itself rather than the property of the function class, Bousquet, O. and Elisseeff, A.(2002). . uniform leave-one-out stability Motivated by the above work, we invent: Object –level uniform leave-one-out stability In short, Object –level stability

76. Definition: We say a algorithm possesses: Object –level uniform leave-one-out stability Abbreviated as Object –level stability, if: Function learned from training data Function learned from training data

77. Generalization based on Object-level Stability Object-level stability The number of training objects With probability at least

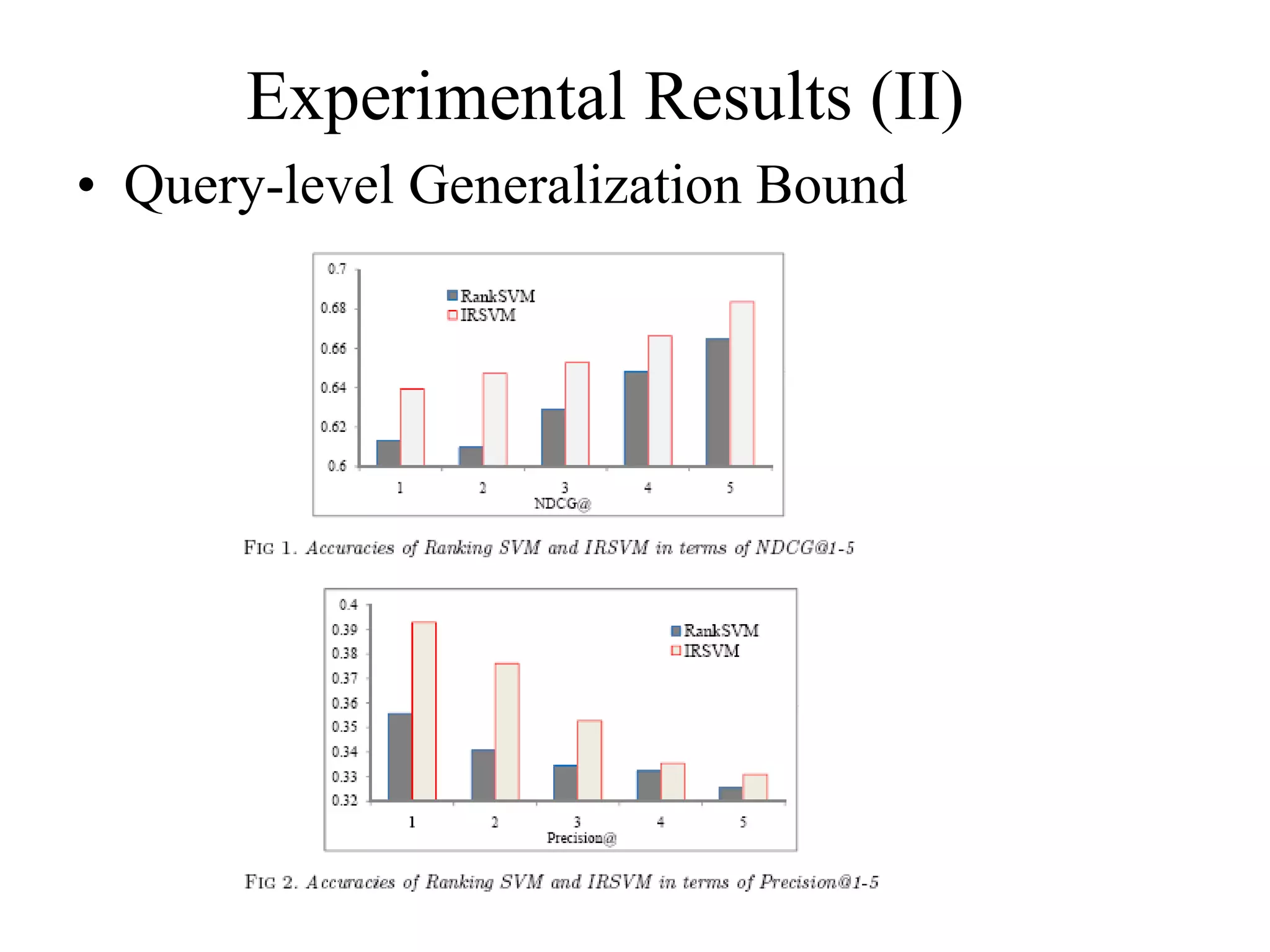
78. Note: if , then the bound makes sense. This condition can be satisfied in many practical cases. As case studies, we investigate Ranking SVM and RankBoost. We show that after introducing query-level normalization to its objective function, Ranking SVM will have query-level stability. For RankBoost , the query-level stability can be achieved if we introduce both query-level normalization and regularization to its objective function . These analyses agree largely with our experiments and the experiments in Y. Cao, J. Xu, T.-Y. Liu, H. Li, Y. Huang, and H.-W. Hon, 2006 [5] and [11].

79. IRSVM : modified Ranking SVM in Y. Cao, J. Xu, T.-Y. Liu, H. Li, Y. Huang, and H.-W. Hon, 2006 query-level normalization Query-level Empirical Risk Generalization Bound:

80. Generalization Bounds Comparison Ranking SVM Generalization Bound: Generalization Bound: Modified RSVM

81. RankBoost with Query-level Normalization and Regularization introducing query-level normalization to RankBoost does not lead to good performance [11]. query-level normalization cannot make RankBoost have query-level stability. adding both query-level normalization and regularization to the objective function, query-level stability can be achieved . Thus the framework offers us a way of modifying RankBoost for good ranking performance

82. Experimental Results (I) Query-Level Stability 1200 queries from a search engine’s data repository. 200 queries for training, 500 queries for validation and 500 queries for test. Five relevance labels and we treat the first three label as “ relevant” and the other ones as “irrelevant” to construct pairs.

83. Query-level Generalization Bound Experimental Results (II)

84. Future Problems and Challenges It is worth to see whether new learning to rank algorithms can be derived under the guide of our theoretical studies. We have investigated the generalization analysis based on the novel two layer statistical learning. We will continue to conduct other theoretical analysis. We have proposed “object-level stability”, we will try to investigate other tools. Two layer statistical learning in other fields

85. Outlines Markov chain methods in search engines Point process describing Browsing behavior Two layer statistical learning Stochstic complement method in ranking Web sites Final remarks

86. Outlines Markov chain methods in search engines Point process describing Browsing behavior Two layer statistical learning Stochstic complement method in ranking Web sites Final remarks

87. We have briefly reviewed part of our recent joint work (in collaboration with Microsoft Research Asia) concerning Internet Information Retrieval. Mathematics is becoming more and more important in the area of Internet information retrieval. Internet information retrieval has been a rich source providing plenty of interesting and challenging problems in Mathematics.

88. Thank you !