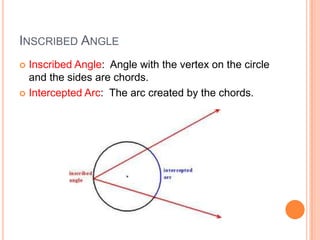
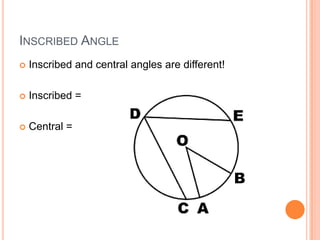
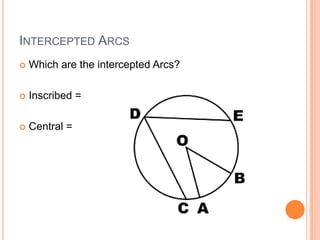
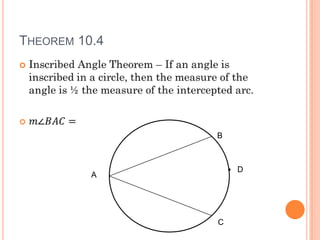
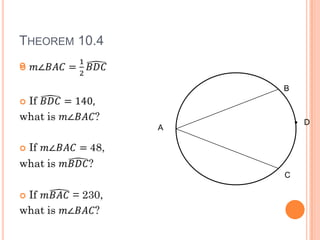
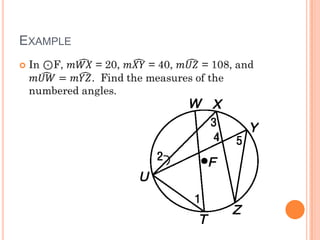
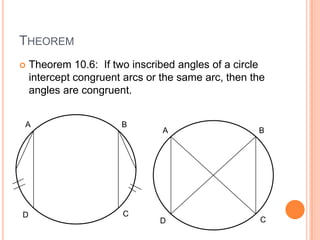
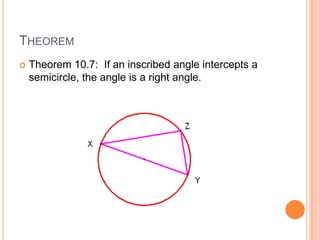
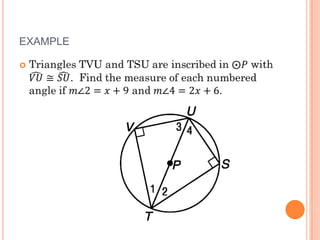
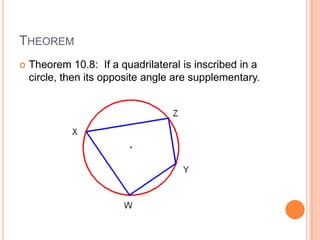
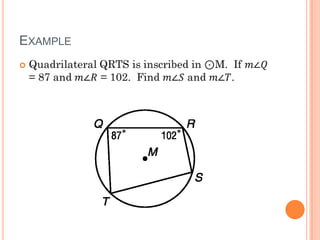
This document discusses inscribed angles and theorems related to them. An inscribed angle is an angle whose vertex is on a circle and whose sides are chords of the circle. The intercepted arc is the arc created by the chords of the inscribed angle. Three theorems are presented: if two inscribed angles intercept congruent arcs, the angles are congruent; if an inscribed angle intercepts a semicircle, the angle is a right angle; and if a quadrilateral is inscribed in a circle, its opposite angles are supplementary. The lesson plan is to introduce inscribed angles and develop theorems about them over two class periods with notes, examples, and a quiz.

1. SECTION 10.4
Inscribed Angles

2. INSCRIBED ANGLES
 How do I find the measure of an inscribed angle?
 How do I find the measures of the angles of an
inscribed polygons?

3. INSCRIBED ANGLE
 Inscribed Angle: Angle with the vertex on the circle
and the sides are chords.
 Intercepted Arc: The arc created by the chords.

4. INSCRIBED ANGLE
 Inscribed and central angles are different!
 Inscribed =
 Central =

5. INTERCEPTED ARCS
 Which are the intercepted Arcs?
 Inscribed =
 Central =

6. THEOREM 10.4

B
D
A
C

7. THEOREM 10.4

B
D
A
C

8. EXAMPLE


9. THEOREM
 Theorem 10.6: If two inscribed angles of a circle
intercept congruent arcs or the same arc, then the
angles are congruent.
A B
A B
D C
D C

10. THEOREM
 Theorem 10.7: If an inscribed angle intercepts a
semicircle, the angle is a right angle.

11. EXAMPLE


12. THEOREM
 Theorem 10.8: If a quadrilateral is inscribed in a
circle, then its opposite angle are supplementary.

13. EXAMPLE


14. HOMEWORK
 Page 549
 #8, 10,
 14 – 30 Even

15. LESSON PLAN
 Intro
 Add a new angle inside a circle, an inscribed angle.
Then develop theorems about inscribed angles.
 Standards- 9.
 Supplies – slides, whiteboard, note sheets
 Timing: One day for notes, one day for a combined
review of 10.3 and 10.4 and a quiz.
 Day 1:
 Essential Questions- slides 2
 Input-slides 3, 6, 9 – 11, 13
 Guided Practice - slides 4, 5, 7, 8, 12, 14
 Independent Practice – Book Work