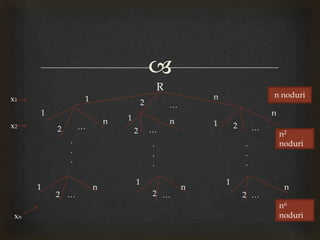
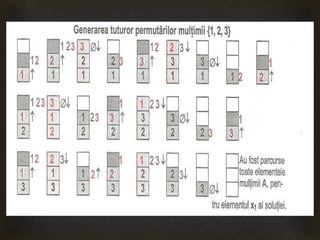
Documentul prezintă metoda backtracking utilizată pentru soluționarea problemelor de căutare prin generarea tuturor soluțiilor posibile. Aceasta implică construirea soluției pas cu pas și renunțarea la valori neviabile, iar metoda este ilustrată prin permutarea elementelor 1, 2, 3, care generează 6 soluții. Se subliniază că backtracking necesită timp îndelungat și ar trebui folosit ca ultimă soluție, exemplificat prin jocul Sudoku.

1. Elaborat de eleva clasei a XI-a “B”
Bondarenco Ana

2. 
 Metoda data se utilizeaza la rezolvarea problemelor
de cautare, generind toate solutiile posibile. Se
construieşte soluţia pas cu pas. Dacă se constată că pentru
o anumită valoare nu se poate ajunge la soluţie, se renunţă
la acea valoare şi se reia căutarea din punctul unde am
rămas.
introducere

3. 

4. 
 In aceasta schema este reprezentat un caz clasic ce
reprezinta esenta metodei backtracking. S-a cerut
permutarea pe diferite pozitii a elementelor 1, 2, 3.
 Ele sunt schimbate cu locurile pina nu sunt parcurse
toate elementele multimii A pentru elementul x a
solutiei. Se obţin 6 soluţii:
1 2 3; 1 3 2; 2 1 3; 2 3 1; 3 1 2; 3 2 1.
*Prin program, rezolvarea aceleiasi probleme , insa cu
n elemente, ar arata astfel:

5. 
Generarea permutărilor mulţimii {1,2,….n}
program permutari;
var
x:array[1..200] of integer;
nr,i,n,k:integer;
function col(k:integer):boolean;
begin
col:=true;
for i:=1 to k-1 do
if x[i]=x[k] then
begin
col:=false;
exit;
end;
end;
begin
write('n=');
readln(n);
nr:=0;
k:=1;
for i:=1 to n do
x[i]:=0;
while k>0 do
if k=n+1 then
begin
k:=k-1;
nr:=nr+1;
writeln(' solutia nr ',nr);
for i:=1 to n do
write(x[i]:2);
readln;
end
else
if x[k]<n then
begin
x[k]:=x[k]+1;
if col(k) then
k:=k+1;
end
else
begin
x[k]:=0;
k:=k-1;
end;
end.

6.  Observaţie: (1,1,…,1) nu este soluţie rezultat, dar e soluţie
posibilă, deci (1,2,…,n) este soluţie rezultat. Numărul
soluţiilor rezultat este n!
Vectorul (x1,…,xk) ∈ (S1,…,Sk), k≥1 verifică aşa
numitele condiţii de continuare, dacă
Φk(x1,…,xk)=true, ϕk : S1xS2x…xSk → {true,false}
Unde *true daca pentru orice i, j de la 1 la k si i diferit
de j si xi diferit de xj
*false daca conditiile nu sunt respectate;

7. 
 Metoda Backtracking utilizează arborele ataşat soluţiilor
posibile pentru a genera soluţiile rezultat, evitând
generarea tuturor soluţiilor posibile prin verificarea
condiţiilor de continuitate ϕk(x1,…,xk).
 Pentru rezolvarea problemei in cauza, poate fi atasat
si un arbore in spatiul solutiilor posibile

8. 
R
1 2
n
…
1
2 …
n 1
2 …
n 1 2 …
n
.
.
.
.
.
.
.
.
.
1
2 …
n
1
2 …
n
1
2 …
n
n nodurin noduri
n2
noduri
nn
noduri
x1
x2
xn

9. 
 ƒ componentele x1,x2,…,xn primesc pe rând valori, adică mai întâi x1, apoi
x2,
 …, deci xk vor primi valoare numai dacă au fost deja stabilite valori pentru
 x1,x2,…,xk-1;
 ƒ dacă xk a primit valoare, nu se trece la nivelul urmator ca să i se atribuie
 valori lui xk+1, fără să se testeze condiţiile de continuare ϕk(x1,…,xk);
 ƒ dacăϕk(x1,…,xk)=true, atunci se încearcă să se dea valori pentru xk+1.
 ƒ dacăϕk(x1,…,xk)=false, atunci:
 a) va trebui o altă alegere pentru xk, dacă Sk nu s-a epuizat sau
 b) dacă Sk s-a epuizat, se revine la nivelul inferior (k-1) şi xk primeşte o
 nouă alegere, abandonându-se un întreg arbore (de aici denumirea
 metodei).
Metoda va genera drumuri de la stânga la dreapta conform
parcurgerii DF(depth, first) a arborilor (în adâncime) şi
anume va genera vectorul (x1,x2,…,xn) astfel:

10. 
 Problemele rezolvate prin aceasta metoda necesita
un timp indelungat, motiv pentru care este bine sa
utilizam metoda numai atunci cand nu avem la
dispozitie un alt algoritm mai eficient. Cu toate ca
exista probleme pentru care nu se pot elabora
algoritmi mai eficienti, tehnica Backtracking trebuie
aplicata numai in ultima instanta. Pentru a intelege
mai bine aceasta metoda, ne putem aminti de
sudoku, un joc care are la baza esenta backtracking.
Concluzie

11. 
 http://info.mcip.ro/?t=back
 http://software.ucv.ro/~cstoica/TP/backtracking.p
df
 http://www.scritub.com/stiinta/informatica/MET
ODA-BACKTRACKING1055131414.php
Linkuri utile