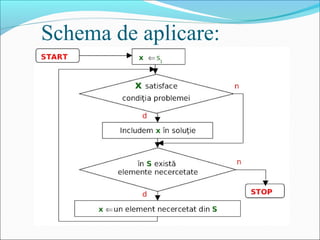
Metoda trierii implică analiza elementelor unei mulțimi finite pentru a găsi soluția unei probleme, utilizând tipuri de date ordinale. Un exemplu dat este elaborarea unui program care determină câte numere din mulțimea naturală <0, ..., n> au suma cifrelor egală cu m, demonstrând astfel aplicația practică a metodei. Deși algoritmii derivați din această metodă sunt relativ simpli, complexitatea lor temporară devine inacceptabilă pentru seturi mari de date, fiind utilizată în principal în scopuri didactice.

1. Tema: Metoda trierii
Realizat de: Vovcioc Raisa
Profesor: Josu Larisa

2. Ce reprezintă metoda trierii:
Metoda trierii presupune că soluţia unei probleme poate fi
găsită analizînd consecutiv elementele si ale unei mulţimi
finite
S = {s1, s2 …, si , …, sk} ,
denumită mulţimea soluţiilor posibile.
În cele mai simple cazuri elementele si ale lui S, pot fi
reprezentate prin valori aparţinînd unor tipuri ordinale de
date:
- integer, - enumerare,
- boolean, - subdomeniu
- char,

3. Schema generală:
Schema generală a unui algoritm bazat pe metoda trierii poate fi
redată cu ajutorul unui ciclu:
For i:=1 to k do if SolutiePosibila(Si) then PrelucrareaSolutiei(Si)
Unde SoluţiaPosibilă este o funcţie booleană care returnează
valoarea truedacă elementul Si satisface condiţiile problemei şi
false în caz contrar, iar PrelucrareaSolutiei este o procedura care
efectuează prelucrarea elementuluiselectat. De obicei, această
procedura soluţia Si este afişată pe ecran.

4. Schema de aplicare:

5. Condiţie:
Se consideră numerele naturale din mulţimea {0, 1, 2, …, n}. Elaboraţi
un program care determină pentru cîte numere K din această mulţime
suma cifrelor fiecărui număr este egală cu m. În particular, pentru
n=100 si m=2, în mulţimea{0, 1, 2, …, 100} există 3 numere care
satisfac condiţiile problemei: 2, 11 si 20.Prin urmare, K=3.
Rezolvare:
Evident, mulţimea soluţiilor posibile S = {0, 1, 2, …, n}. În programul
ceurmează suma cifrelor oricărui număr natural i, i S, se calculează cu∈
ajutorulfuncţiei SumaCifrelor. Separarea cifrelor zecimale din scrierea
număruluinatural “i” se efectuează de la dreapta la stinga prin
împărţirea numărului “i” sia cîturilor respective la baza 10.

6. Avantajul principal al algortmilor bazaţi pe metoda trierii
constă în faptul că programele respective sînt relative
simple, iar depanarea lor nu necesita teste sofisticate.
Complexitatea temporală a acestor algoritmi este
determinată denumărul de elemente k din mulţimea soluţiilor
posibile S. În majoritatea problemelor de o reala importanţă
practica metoda trierii conduce la algoritmii exponenţiali.
Întrucit algoritmii exponenţiali sînt inacceptabili in
cazul datelor de intrare foarte mari, metoda trierii este
aplicată numai în scopuri didactice sau pentru elaborarea
unor programe al căror timp de execuţie nu este critic.

7. Manual de Informatică clasa a 11-a
( Anatol Gremalschi, Ştiinţa 2008)

8. 1.1.
http://ro.scribd.com/doc/60874739/Proiect-la-informaticahttp://ro.scribd.com/doc/60874739/Proiect-la-informatica
2.
http://www.didactic.ro/materiale-didactice/12084_metoda-