Recommended
More Related Content
More from matsushimalab
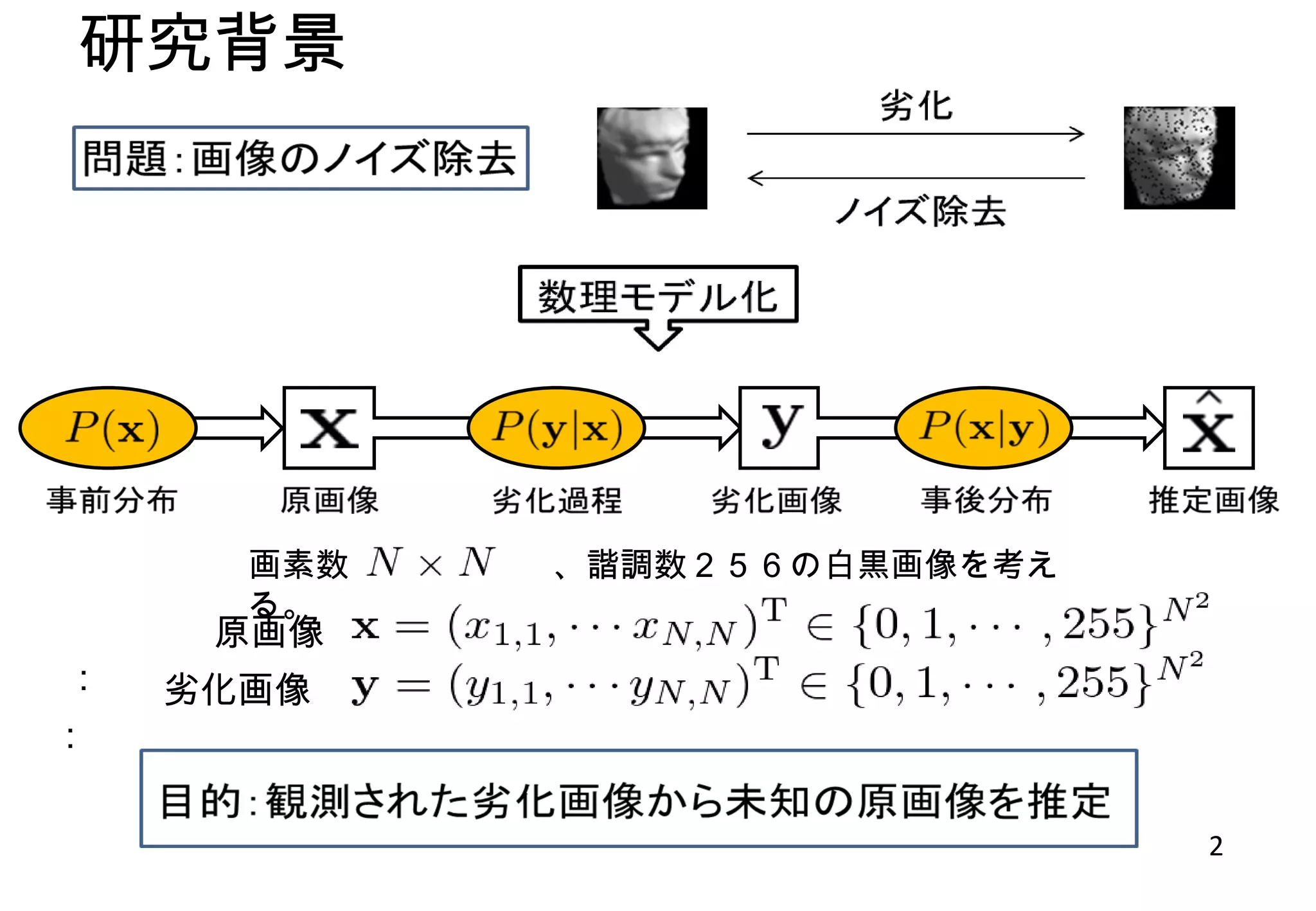
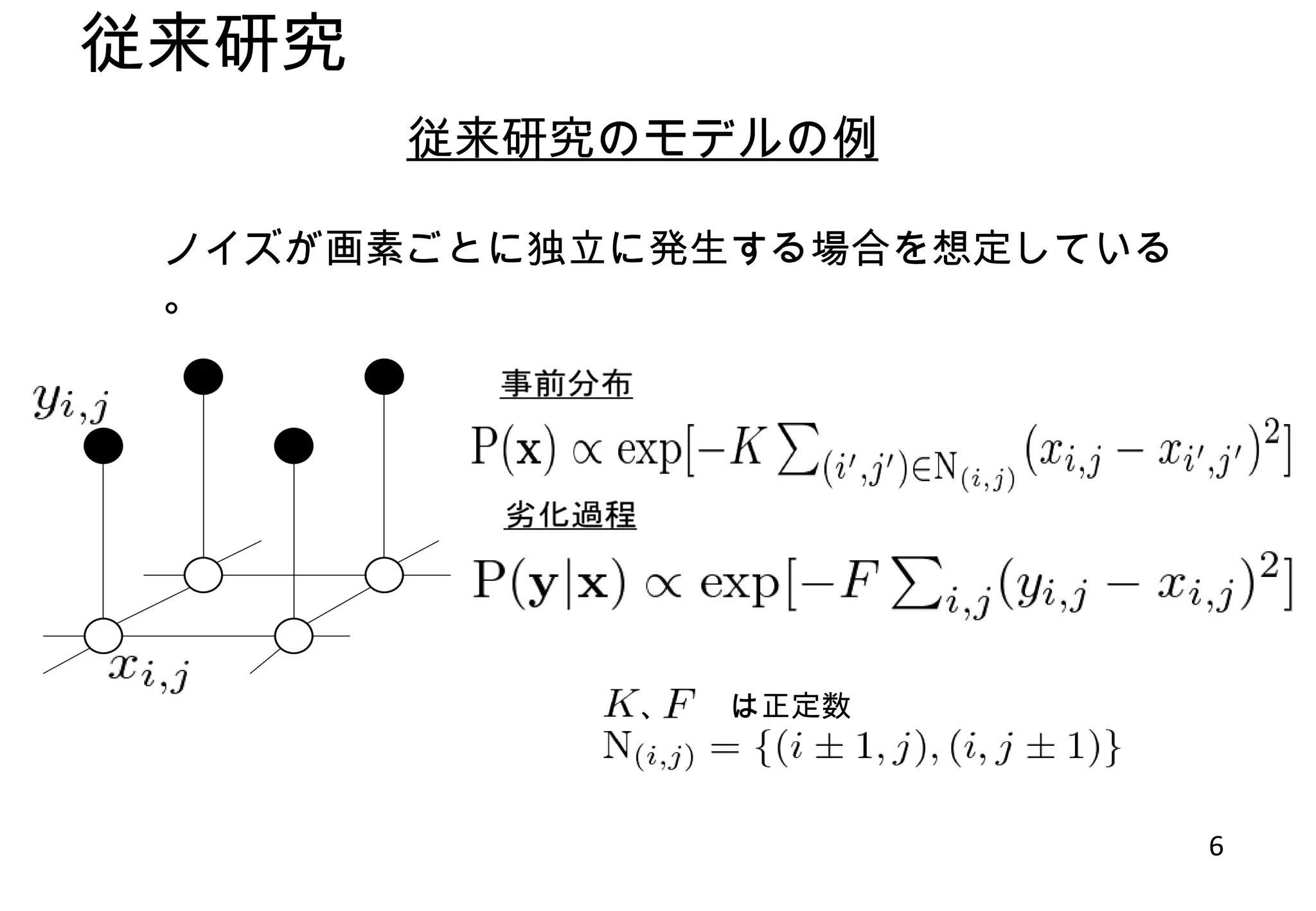
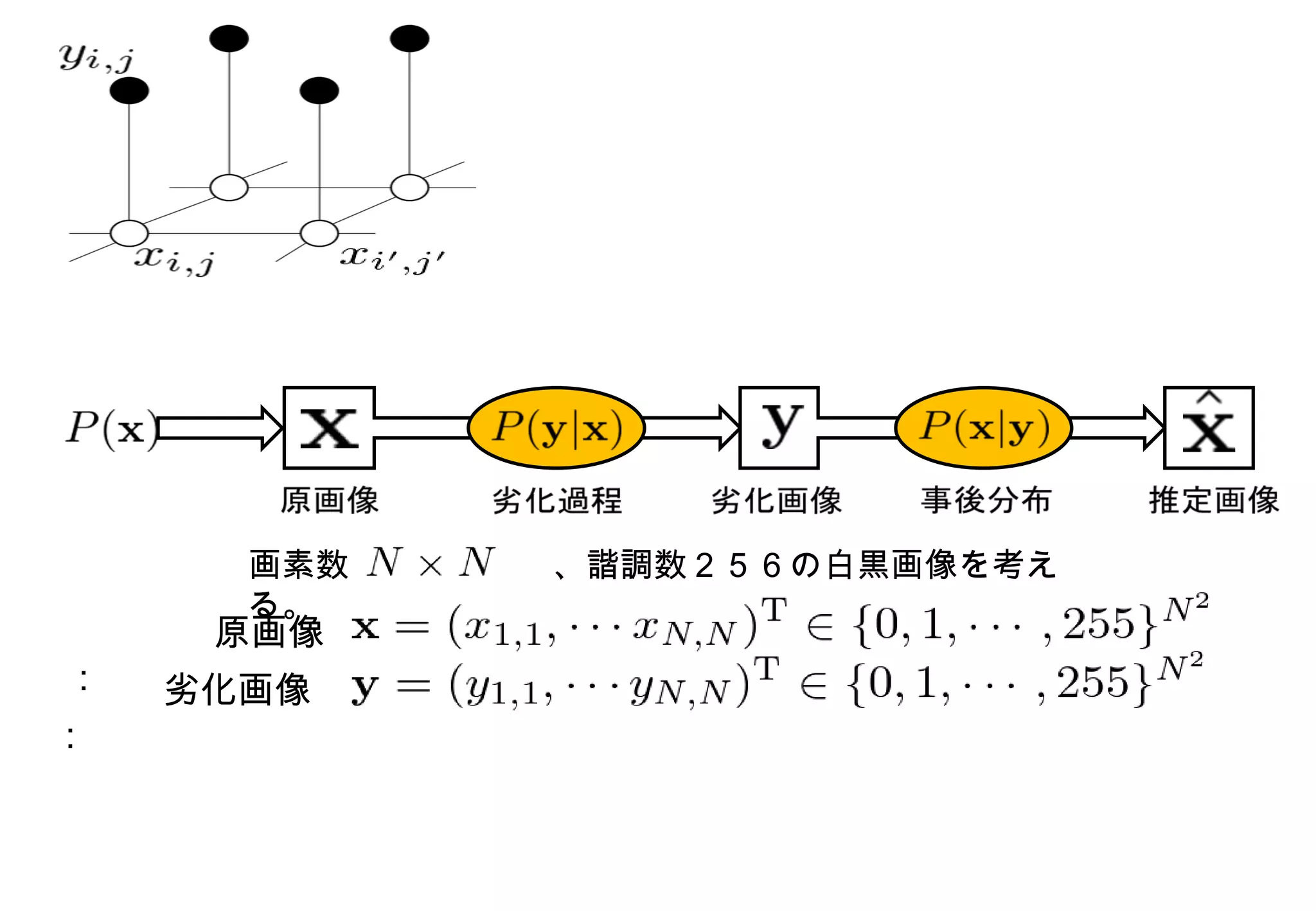
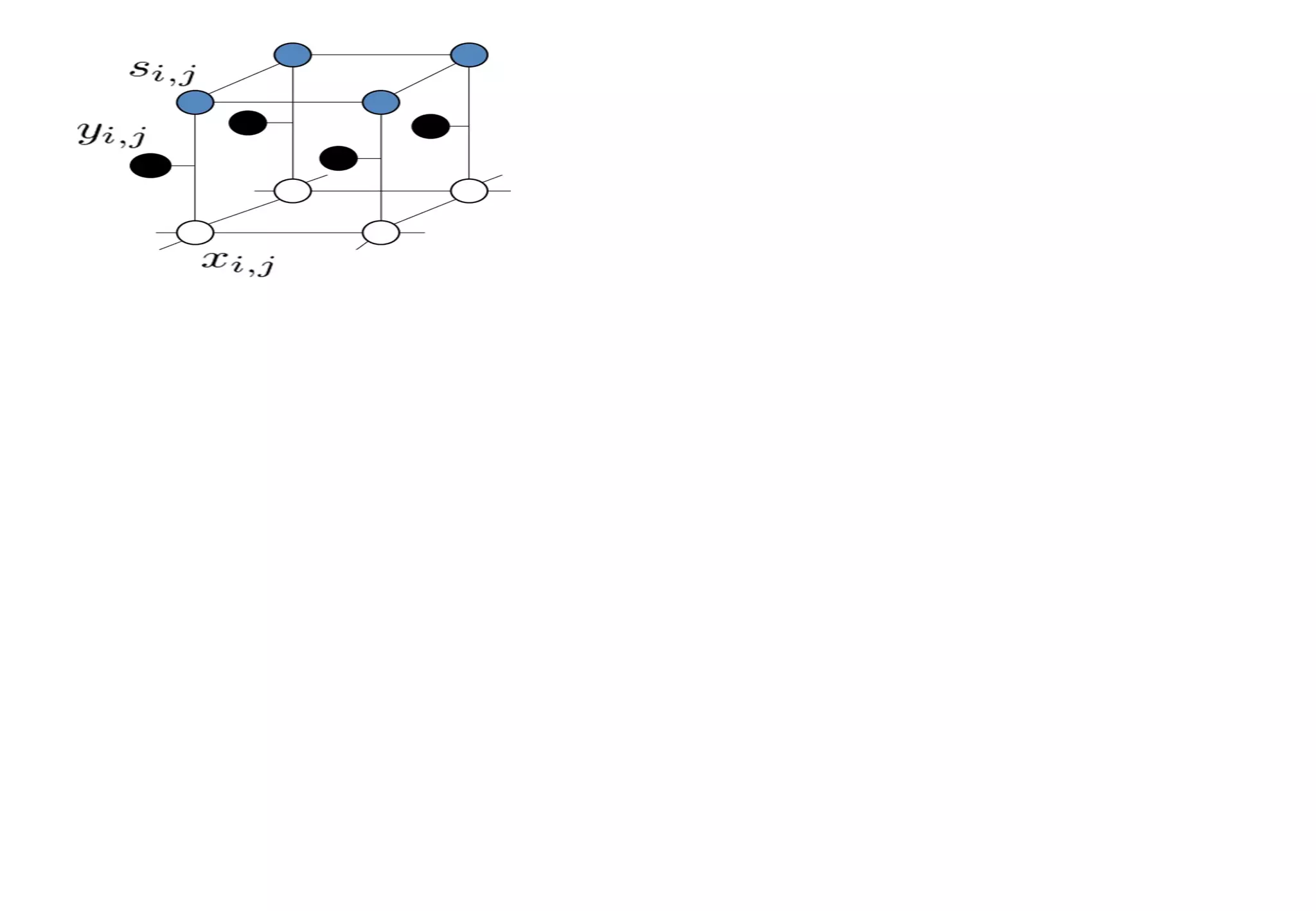
ma99992010id497
- 1. 画像のノイズ除去に対するモデルの提案 指導 松嶋敏秦 教授 早稲田大学基幹理工学部応用数理学科 深田章悟 ２０１０年度卒業論文 １
- 2. 研究背景 2 画素数 、諧調数２５６の白黒画像を考える。 劣化画像 ： 原画像 ：
- 4. 研究目的 ノイズが固まって発生しやすい場合を想定したモデルの提案 従来研究のモデルの問題点 劣化過程としてノイズが独立に発生する場合を想定 ノイズが相関を持って発生する場合には不適 4 視点：画像のノイズ除去のモデル化 適切な事前分布 と劣化過程 を設定すること 事後分布 は事前分布と劣化過程により定まる。 研究の目的 ベイズの公式 ：
- 6. 従来研究 6 、 は正定数 ノイズが画素ごとに独立に発生する場合を想定している。 従来研究のモデルの例
- 7. 提案するモデル 7 ただし、 ノイズが隣接して発生しやすい場合を想定する。
- 9. まとめと課題 8
Editor's Notes
- 私の研究の問題は画像のノイズ除去というものです。 実際の画像で簡単に説明すると、何らかの原因によって劣化された画像をノイズを除去することによって画像を元の画像、あるいはそれに近い画像に復元することを目的としています。 この問題を数理モデルかするとこのようになります。 この図は、原画像 X は事前分布 PX に従い生成され、劣化過程により X は Y に変換され、最後に事後分布によって原画像が推定されるということを表しています。 本研究では、画素数が N×N で、諧調数が２５６の白黒画像を考えます。 原画像、劣化画像は成分がそれぞれ０から２５５までの整数をとり、成分の数が N の２乗個のベクトルで表現します。 そしてこの問題の目的は、観測された劣化画像から未知の原画像を推定することにあります。