The document proposes reducing the computational complexity of message passing algorithms like belief propagation (BP) and concave-convex procedure (CCCP) for multiuser detection in CDMA systems. It does this by changing the factor graph structure used to represent the detection problem from a fully connected graph (Factor Graph I) to a sparsely connected graph (Factor Graph II). Simulation results show the proposed CCCP detector for the new factor graph achieves near optimal performance with lower complexity than existing approaches.

1. Multiuser Detection Algorithms for CDMA based on the Message Passing Algorithms Waseda University, Japan Shunsuke Horii Tota Suko Toshiyasu Matsushima

2. 1 ． Introduction 2 ． CDMA model and multiuser detection 3 ． The belief propagation and the concave convex procedure 4 ． Detection algorithms based on the message passing algorithms 5 ． Some performance analysis based on the numerical simulations 6 ． Discussions 7 ． Conclusion Contents

3. Optimal detector for CDMA The MPM detector is optimal with respect to the Bit Error Rate. But the computational complexity of the MPM detector increases exponentially with the number of users. -> There are many researches about alternative detectors. １． Introduction detection problem can be regarded as a probabilistic inference problem Message passing algorithms defined in terms of operations on a graph compute marginal probability function efficiently Recently, detectors based on the message passing algorithms were developed. But it have been reported that the computational complexity of the message passing algorithms for the detection problem also increases exponentially with the number of users. [Kabashima, 2003] [Tonosaki et al., 2004]

4. In this study, we suggest that we can reduce the computational complexity of the message passing algorithms for the detection problem by converting the graph structure . １． Introduction

5. 2 ． Synchronous DS CDMA Channel Model with K users 【information bit】 【signature sequence】 ： number of chips ： chip cycle 【modulated signal】

6. 2 ． Synchronous DS CDMA Channel Model with K users Channel receiver Gaussian noise The signals of all users are multiplexed. Gaussian noise is added.

7. MPM detector is optimal with respect to the Bit Error Rate (BER) : 【 MPM (Maximum Posterior Marginal) detector 】 Uniform Prior: Gaussian Channel: 3 ． MPM detector

8. MPM detector is optimal. But it’s computational complexity is . Reduced computational complexity and good approximation algorithm is necessary. The detection problem can be regarded as a probabilistic inference problem . There are many algorithms which compute a marginal of a posterior distribution efficiently, such as the Belief Propagation (BP) and the Concave-Convex Procedure (CCCP) . 3 ． MPM detector Computational Complexity Problem

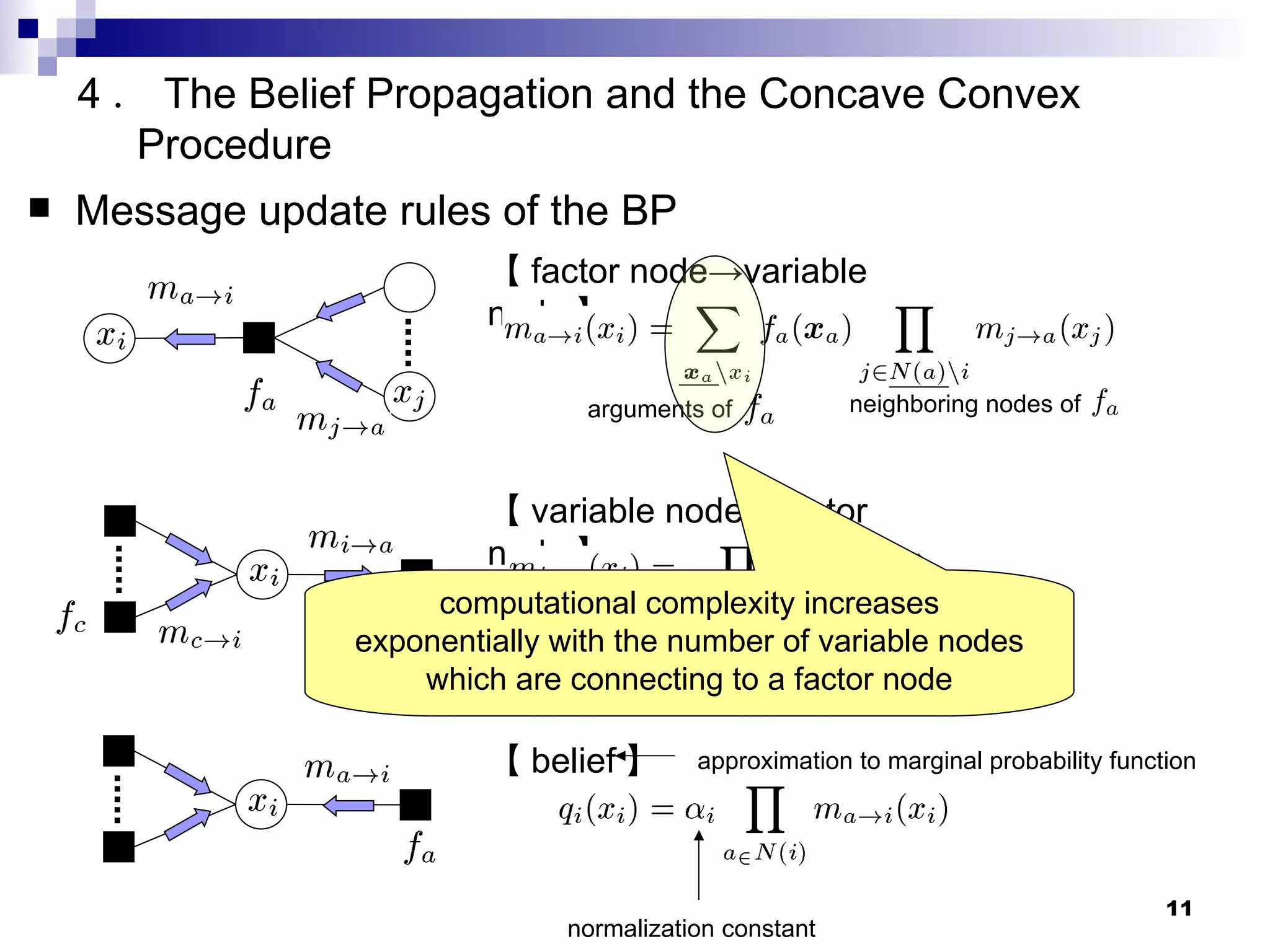
9. 【 Factor Graph (FG) 】 A bipartite graph which expresses the structure of a factorization of a joint distribution. The BP and the CCCP can be defined in terms of operations on a factor graph. 4 ． The Belief Propagation and the Concave Convex Procedure Ex. [Kschischang et al. 01]

10. The BP and the CCCP When the factor graph has many cycles, the BP and the CCCP both compute an approximation to a marginal probability function of each variable. the BP does not always converge , while the CCCP is stable and probably convergent even when the BP does not converge . If the algorithms converge, the fixed point of the BP correspond to that of the CCCP. 4 ． The Belief Propagation and the Concave Convex Procedure [Yedidia et al. 2005] [Yuille, 2002 ]

11. Message update rules of the BP neighboring nodes of 【 factor node->variable node 】 arguments of neighboring nodes of 【 variable node->factor node 】 【 belief 】 approximation to marginal probability function normalization constant 4 ． The Belief Propagation and the Concave Convex Procedure computational complexity increases exponentially with the number of variable nodes which are connecting to a factor node

12. CCCP is a double loop algorithm update rules of the outer loop the number of neighboring factor nodes of the variable node convergent value of in the inner loop update rules of the inner loop 4 ． The Belief Propagation and the Concave Convex Procedure After the enough number of the updates in the inner loop, the convergent value of the λ ai is used for the updates in the outer loop. computational complexity increases exponentially with the number of variable nodes which are connecting to a factor node

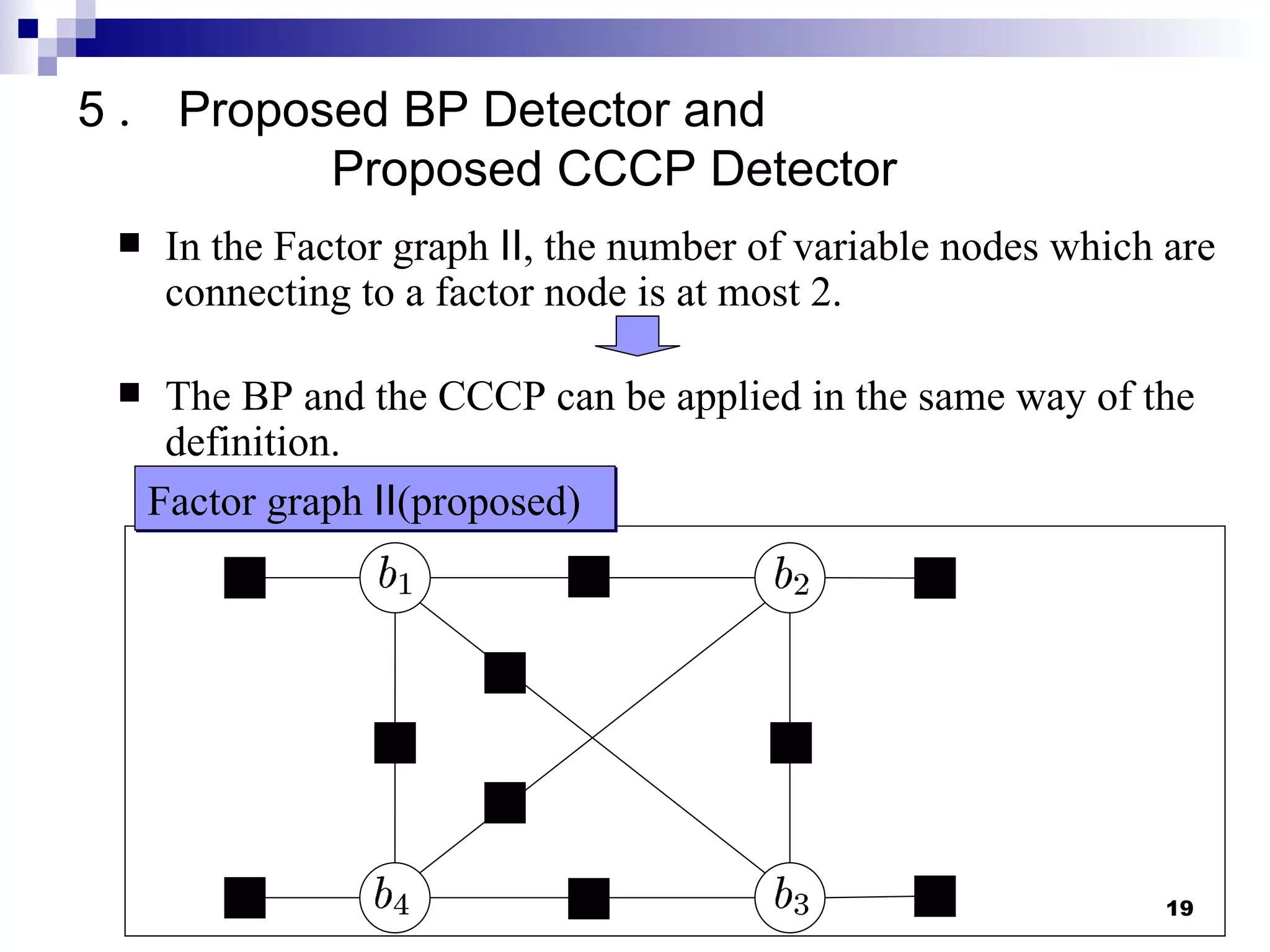
13. In the past researches, the BP and the CCCP are already applied for the detection problem. 5 ． Approximate BP Detector and Approximate CCCP Detector Factor graph Ⅰ [Kabashima, 2003] [Tonosaki et al., 2004]

14. Number of the variable nodes which are connecting to a factor node is K. 5 ． Approximate BP Detector and Approximate CCCP Detector The computational complexities of the BP and the CCCP become Update rule for the message of the BP Update rule for the inner loop of the CCCP

15. To resolve the problem they reduced computational complexities of the algorithms through approximation. Assumption: 5 ． Approximate BP Detector and Approximate CCCP Detector

16. Factor graph expresses the structure of the factorization of a function. We convert the graph structure by changing the factorization. 5 ． Proposed BP Detector and Proposed CCCP Detector Point There are many ways to factorize. Point in our proposition

17. 5 ． Proposed BP Detector and Proposed CCCP Detector The posterior distribution can be factorized as follows: Sufficient statistics Cross correlations

18. 5 ． Proposed BP Detector and Proposed CCCP Detector The posterior distribution can be factorized as follows: Factor graph Ⅱ(proposed)

19. 5 ． Proposed BP Detector and Proposed CCCP Detector In the Factor graph Ⅱ, the number of variable nodes which are connecting to a factor node is at most 2. The BP and the CCCP can be applied in the same way of the definition. Factor graph Ⅱ(proposed)

20. 6 ． Simulations Simulation Conditions Ⅰ ． Comparison of the detectors with the bit error rate ※ assumption to approximate

21. 6 ． Simulations The performance of the BP for the Factor Graph Ⅱis not good. The performance of the CCCP for the Factor Graph Ⅱis near to the MPM detector’s performance

22. The performance of the BP for the Factor graph Ⅱ is improved. The performance of the approx. CCCP for the FG Ⅰ is not good. 6 ． Simulations ※Absolute values of the cross correlations tends to take small values when the length of the signature sequence is large.

23. 6 ． Simulations Simulation Conditions Ⅱ ． Comparison of the approx. CCCP for the FGⅠ and the CCCP for the FGⅡ

24. 6 ． Simulations The bit error rate of the approx. CCCP for the Factor Graph Ⅰ doesn’t decrease for the increase in the number of updates in the outer loop.

25. 6 ． Simulations The bit error rate of the approx. CCCP for the Factor Graph Ⅰdecreases for the increase in the number of updates in the outer loop. imply The approx. CCCP for the Factor Graph Ⅰ needs more number of updates in the Inner loop.

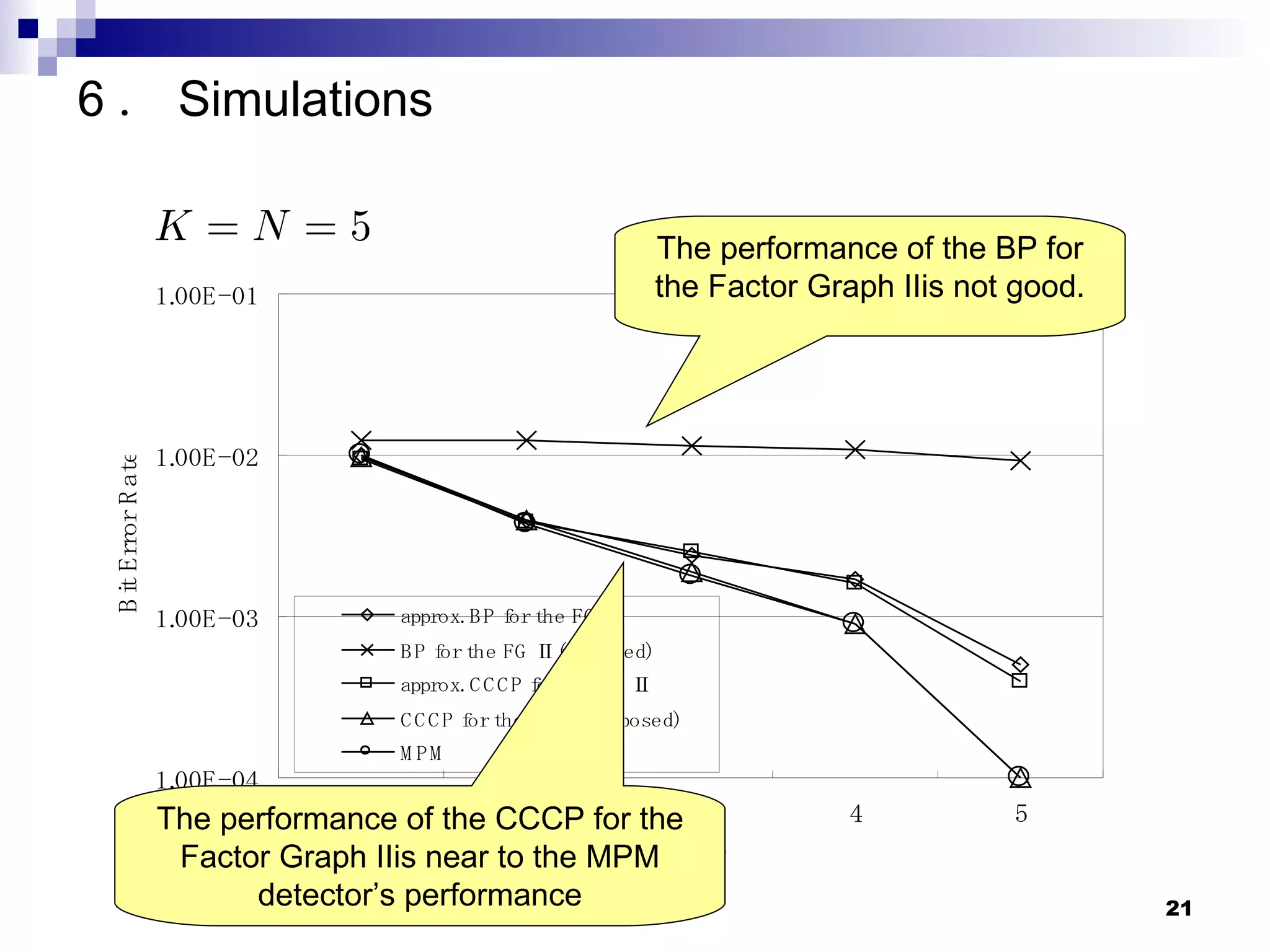
26. 7 ． Discussions Relations between the graph structure and the performances of the detectors. The BP is not appropriate for the factor graph Ⅱ when the absolute values of the cross correlations are large. Reason It seems to me that the fact that “the strengths of functions are strong, the BP tends to not converge” is one of reasons. Ref.[Welling and Teh, 2001] ※

27. 7 ． Discussions Relations between the graph structure and the algorithms The CCCP for the Factor graph Ⅱ outperform the approximate CCCP for the Factor graph Ⅰ. Reason It seems to me, the number of edges effects on the necessary number of updates for the CCCP to converge. The number of edges is reduced in the Factor graph Ⅱ.

28. We showed that we can reduce the computational complexity of the BP and the CCCP for the detection problem by converting the graph structure. 8 ． Conclusion We obtained the relations between the graph structure and the performances of the algorithms with computer simulations.

29. Appendix A

30. Appendix B