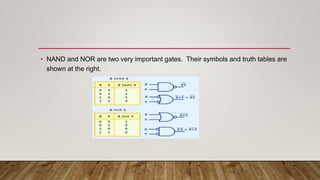
The document covers the fundamentals of logic gates and circuits, highlighting the connection between boolean logic and digital computer circuits, as well as the importance of simplifying boolean functions for efficient circuit design. It discusses various boolean operations, laws, and the significance of different logic gates, including AND, OR, NOT, NAND, and NOR. Additionally, it explains characteristics of logic families and various types of bipolar transistor families used in integrated circuits.

1. UNIT2
LOGIC GATES AND CIRCUITS

2. OBJECTIVES
• Understand the relationship between Boolean logic and digital computer circuits.
• Learn how to design simple logic circuits.
• Understand how digital circuits work together to form complex computer systems.

3. INTRODUCTION
• In the latter part of the nineteenth century, George Boole incensed philosophers and
mathematicians alike when he suggested that logical thought could be represented through
mathematical equations.
• How dare anyone suggest that human thought could be encapsulated and
manipulated like an algebraic formula?
• Computers, as we know them today, are implementations of Boole’s Laws of Thought.
• John Atanasoff and Claude Shannon were among the first to see this connection.

4. • In the middle of the twentieth century, computers were commonly known as “thinking
machines” and “electronic brains.”
• Many people were fearful of them.
• Nowadays, we rarely ponder the relationship between electronic digital computers and
human logic. Computers are accepted as part of our lives.
• Many people, however, are still fearful of them.
• In this chapter, you will learn the simplicity that constitutes the essence of the machine.

5. BOOLEAN ALGEBRA
• Boolean algebra is a mathematical system for the manipulation of variables that can have
one of two values.
• In formal logic, these values are “true” and “false.”
• In digital systems, these values are “on” and “off,” 1 and 0, or “high” and “low.”
• Boolean expressions are created by performing operations on Boolean variables.
• Common Boolean operators include AND, OR, and NOT.

6. AND, OR OPERATION
• A Boolean operator can be completely described
using a truth table.
• The truth table for the Boolean operators AND
and OR are shown at the right.
• The AND operator is also known as a Boolean
product. The OR operator is the Boolean sum.

7. NOT OPERATION
• The truth table for the Boolean NOT operator
is shown at the right.
• The NOT operation is most often designated
by an overbar. It is sometimes indicated by a
prime mark ( ‘ ) or an “elbow” ().

8. FUNDAMENTAL LAWS
•Associative laws
•(A + B)+ C = A+ (B + C)
•(AB)C = A (BC)
• Distributive laws
•A (B + C) = AB + AC

9. •Related identities
•(A + AB)= A
•(A + B)= A+ B
•(A+B)• (A+C) =(A+BC)
•Commutative Law
•A + B = B + A

10. • It implies that the input A and B of the OR gate can be interchanged without changing
the output Y. It can be justified from the truth table of two-input OR gate. For A = B, it
is obvious that it doesn’t matter when we interchange A and B. When A = 0 and B = 1, if
we interchange A and B, then it will become the case of A = 1 and B = 0 and for both
these case the output is 1. Hence it doesn’t matter to the output if we interchange A and B
inputs.
• Associative Law
• A + B + C = (A + B) + C = A + (B + C)

11. BOOLEAN FUNCTION
• A Boolean function has:
• At least one Boolean variable,
• At least one Boolean operator, and
• At least one input from the set {0,1}.
• It produces an output that is also a member of the set {0,1}.

12. • The truth table for the Boolean function:
F(X,Y,Z)=X 𝑧+Y
is shown at the right.
• To make evaluation of the Boolean function easier, the truth
table contains extra (shaded) columns to hold evaluations of
subparts of the function.

13. • As with common arithmetic, Boolean operations have rules of
precedence.
• The NOT operator has highest priority, followed by AND and
then OR.
• This is how we chose the (shaded) function subparts in our
table.

14. • Digital computers contain circuits that implement Boolean functions.
• The simpler that we can make a Boolean function, the smaller the circuit that will result.
• Simpler circuits are cheaper to build, consume less power, and run faster than
complex circuits.
• With this in mind, we always want to reduce our Boolean functions to their simplest form.
• There are a number of Boolean identities that help us to do this.

15. DE MORGAN'S THEOREM
• Sometimes it is more economical to build a circuit using the complement of a function
(and complementing its result) than it is to implement the function directly.
• DeMorgan’s law provides an easy way of finding the complement of a Boolean function.
• Recall DeMorgan’s law states:
• 𝑥𝑦 = 𝑥 + 𝑦 and 𝑥 + 𝑦 = 𝑥 𝑦

16. • DeMorgan’s law can be extended to any number of variables.
• Replace each variable by its complement and change all ANDs to ORs and all ORs to
ANDs.
• Thus, we find the the complement of:
𝐹 𝑋, 𝑌, 𝑍 = (𝑋𝑌)+( 𝑥𝑍) + 𝑌 𝑧)
𝐹 𝑋, 𝑌, 𝑍 = 𝑥𝑦 + 𝑥𝑧 + 𝑦 𝑧
= 𝑥𝑦 𝑥𝑧 𝑦 𝑧
= 𝑥 + 𝑦 𝑥 + 𝑍 𝑦 + 𝑧

17. LOGIC GATES
• The three simplest gates are the AND, OR, and NOT gates.
• They correspond directly to their respective Boolean operations, as you can see by their
truth tables.

18. • Another very useful gate is the exclusive OR (XOR) gate.
• The output of the XOR operation is true only when the values of the inputs differ.

19. • NAND and NOR are two very important gates. Their symbols and truth tables are
shown at the right.

20. • NAND and NOR are known as universal gates because they are inexpensive to
manufacture and any Boolean function can be constructed using only NAND or only
NOR gates.

21. • Gates can have multiple inputs and more than one output.
• A second output can be provided for the complement of the operation.
• We’ll see more of this later.

22. CHARACTERISTICS OF LOGIC FAMILIES
• The main characteristics of logic families include:
• Speed
• Fan-in
• Fan-our
• Noise immunity
• Power dissipation

23. • Speed:speed of a logic circuits is determined by the time between the application of input
and change in the output of the circuits.
• Fan-in:It determines the number of inputs the logic gate can handle.
• Fan-out:Determines the number of circuits that a gate can drive.
• Noisy immunity:Maximum noise that a circuit can withstand without affecting the output.
• Power:When a circuit switches from one state to other ,power dissipates.

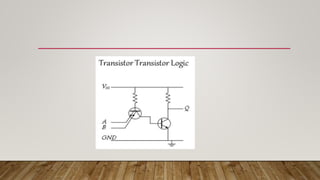
24. BIPOLAR FAMILIES
• Bipolar transistors are fabricated on a chip in digital integrated circuits.
• Bipolar technology is preferred for SSI[Small scale integrated]and MS[Medium scale
integration]because it is faster.
• TYPES OF BIPOLAR FAMILIES:
• Diode Logic(DL)
• Register Transistor Logic(RTL)
• Diode Transistor Logic
• Transistor-Transistor Logic

25. DIODE LOGIC
In DDL(diode logic),only Diode and Resistors are used for implementing a particular
logic.Remember that the Diode conducts only when it is Forward Biased.

26. • DISADVANTAGES OF DIODE LOGIC:
• Diode Logic suffers from voltage degradation from one stage to the next.
• Diode Logic only permits OR and AND functions.

27. RESISTOR TRANSISTOR LOGIC
• In RTL(resistor transistor logic),all the logic are implemented using resistors and
transistors.one basic thing about the transistor(NPN),is the HIGH at input causes output to
be LOW (i.e.like a inverter).in the case of PNP transistor,the LOW at input causes ouput
to be HIGH.

28. • ADVANTAGE:
• Less number of transistors
• DISADVANTAGES:
• High power dissipation
• Low fan in

29. DIODE TRANSISTOR LOGIC
• In DTL(Diode transistor logic),all the logic is implemented using diodes and transistors.
• DISADVANTAGE:
• Propogation delay is larger

30. TRANSISTOR TRANSISTOR LOGIC
• The first transistor-transistor logic family of integrated circuits was introduced by
Sylvania as Sylvania universal high-level logic(SUHL)in 1963 Texas instruments
introduced 7400 series TTL family in 1964.
• Transistor –transistor logic uses bipolar transistor to form its integrated circuits.
• TTL has changed significantly over the years,with newer versions replacing the old types.

32. INTEGRATED CIRCUITS
• When integrated circuits are used,one or more complete gates or other circuits are
packaged in a single integrated –circuits(IC)container.
• The IC containers provide input and output pins or connections,which or then
interconnected by plated strips on circuit boards,wires,or other means.to form complete
computing devices.
• There are two basic techniques for manufacturing ICs-bipolar and metal-oxide
semiconductor(MOS).

33. THANK YOU