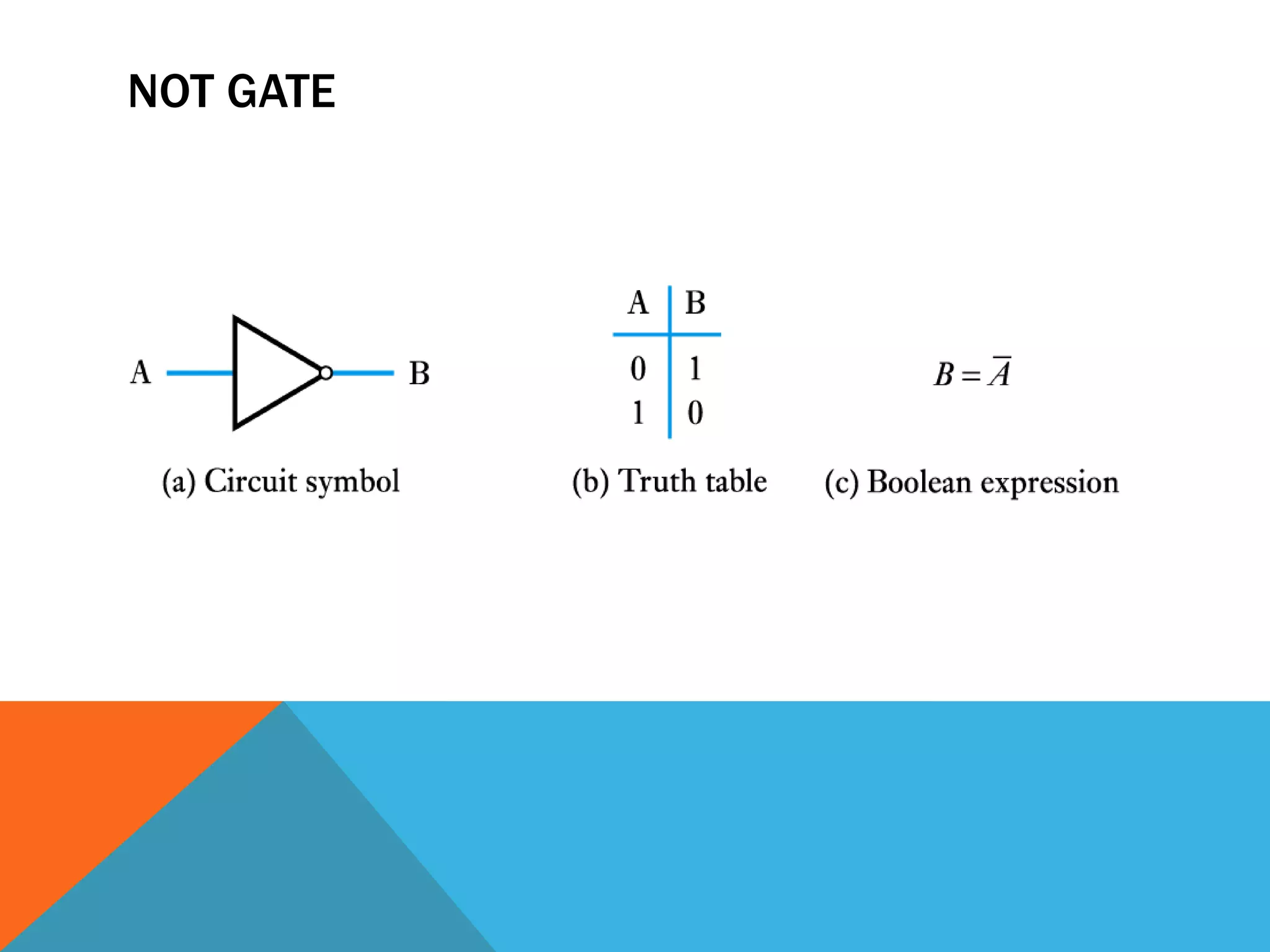
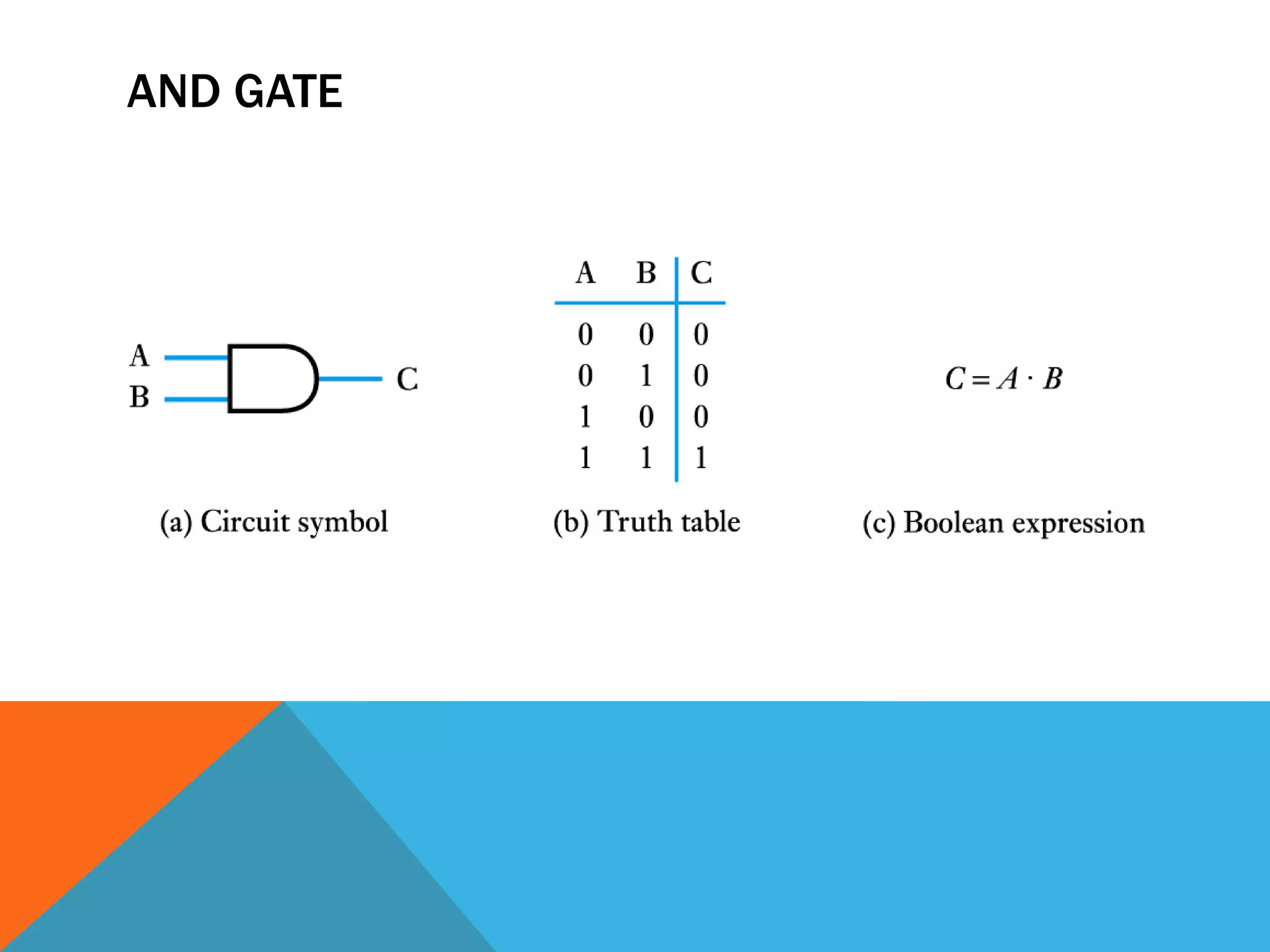
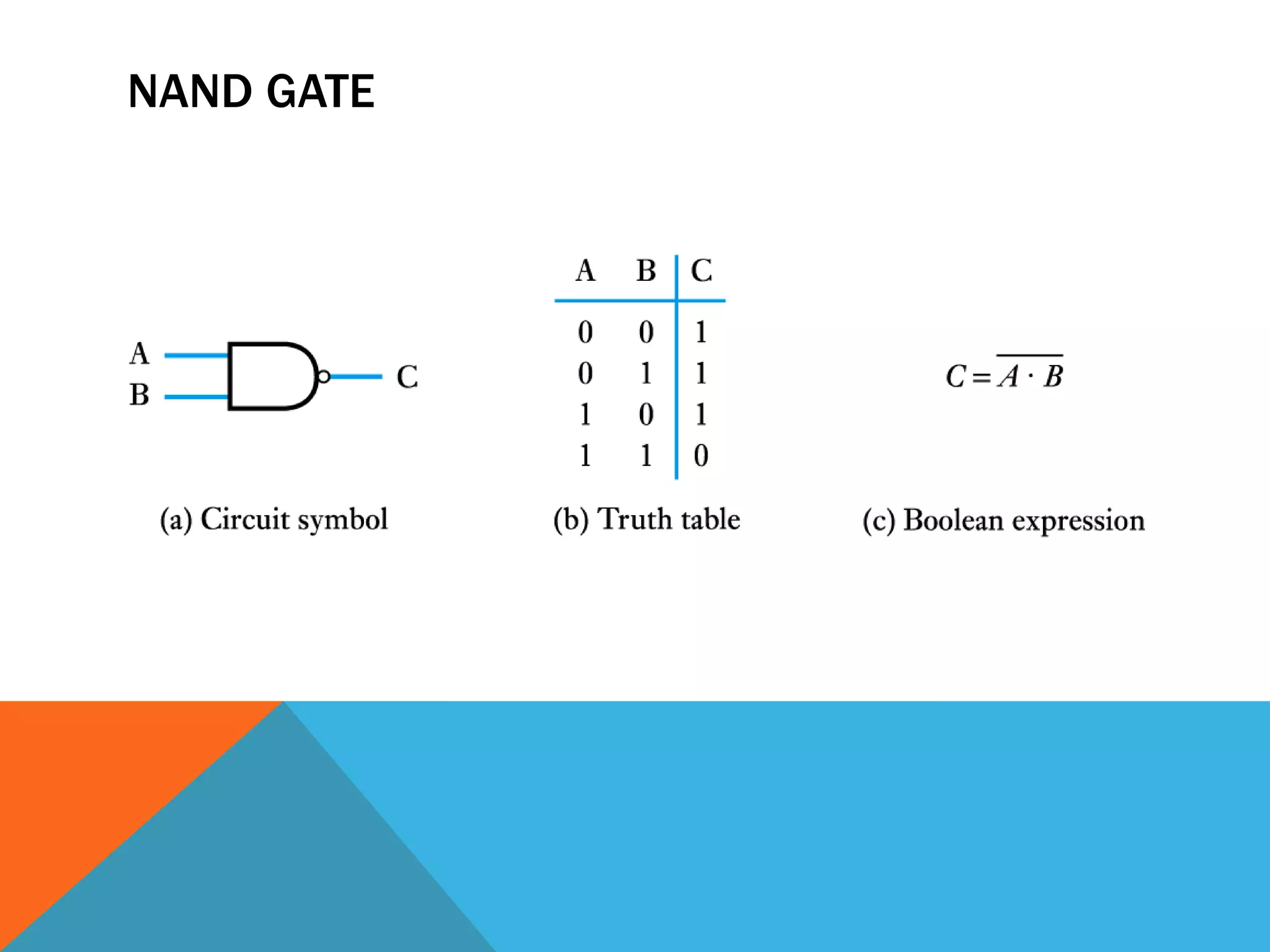
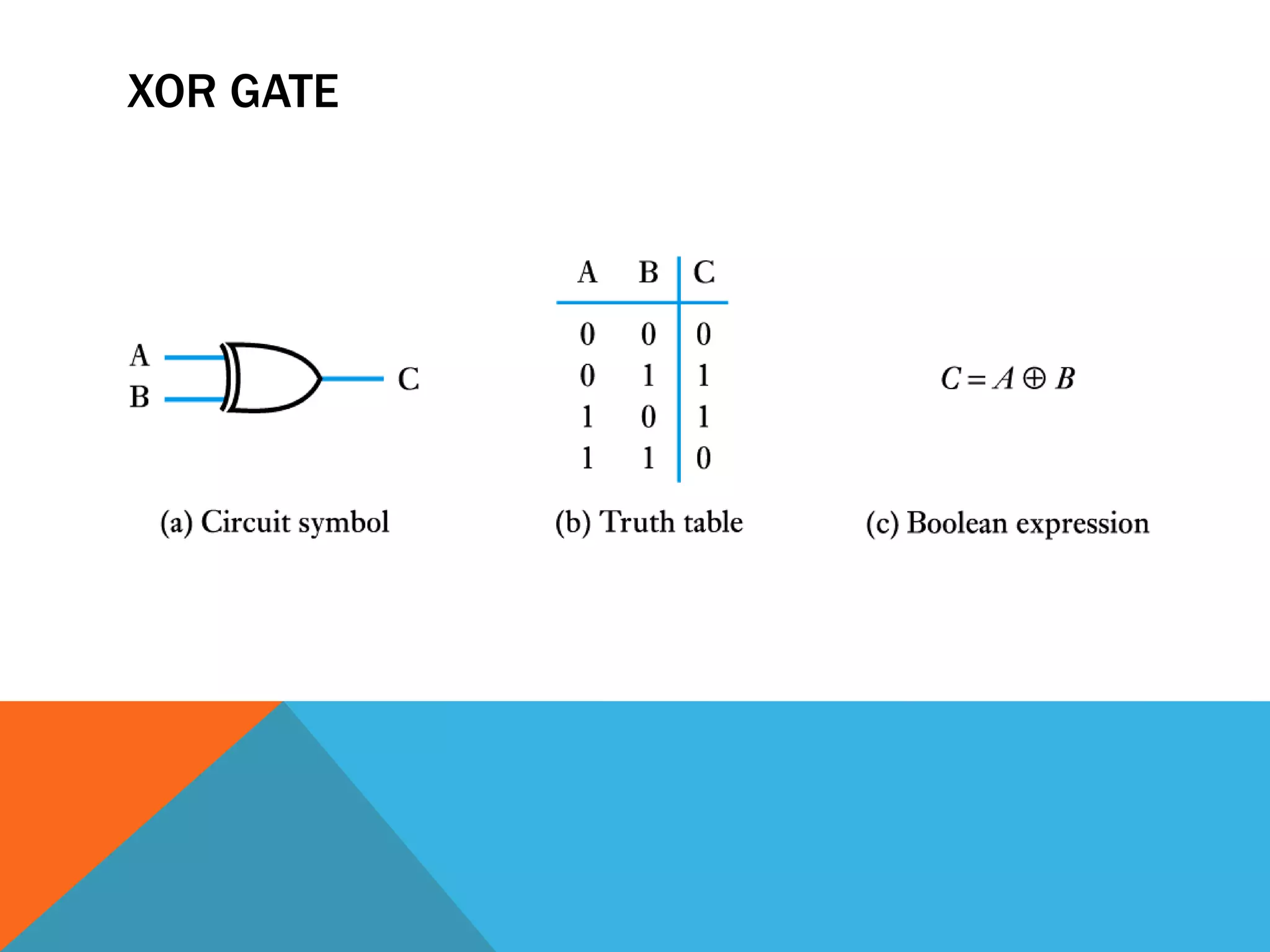
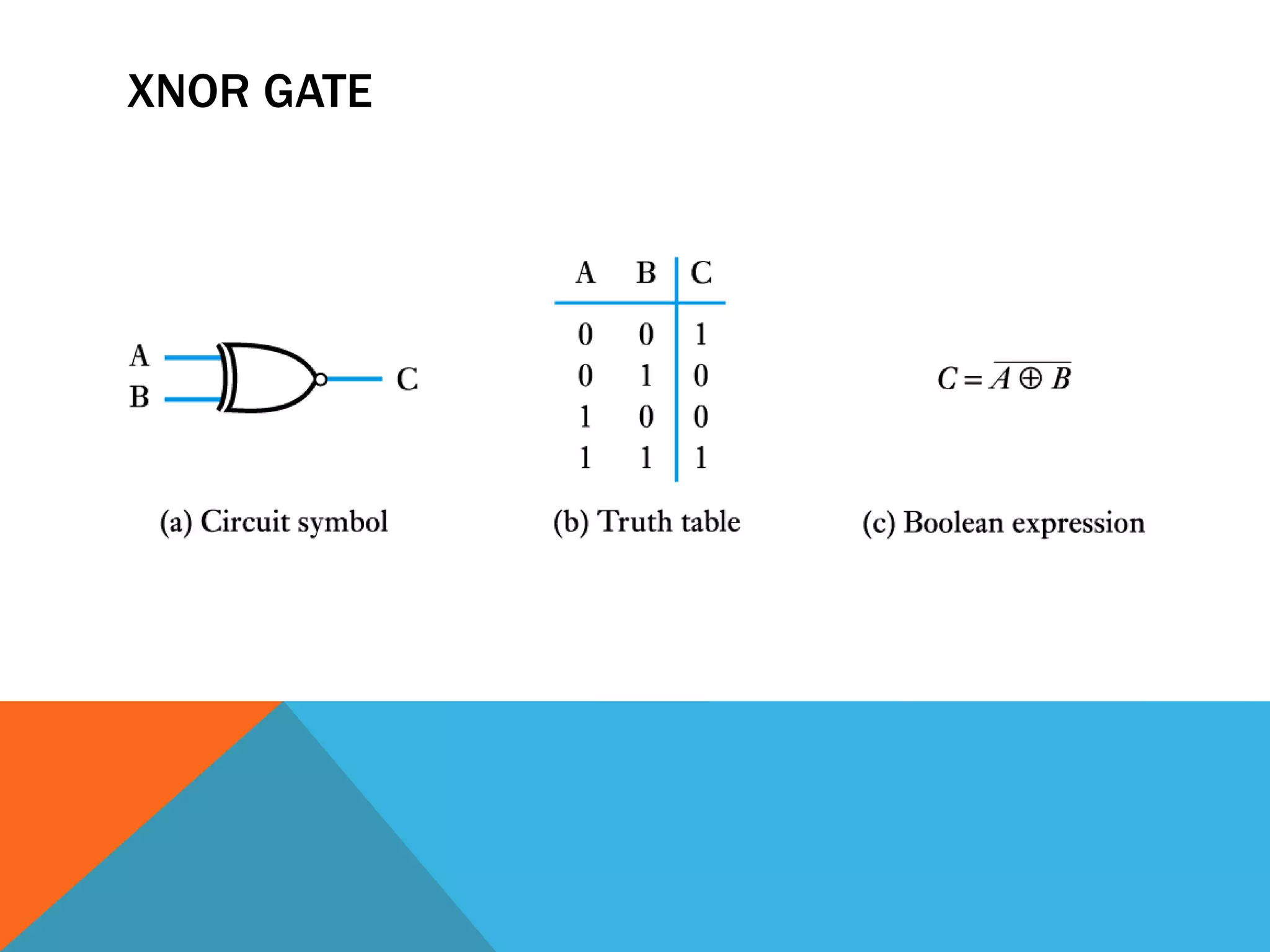
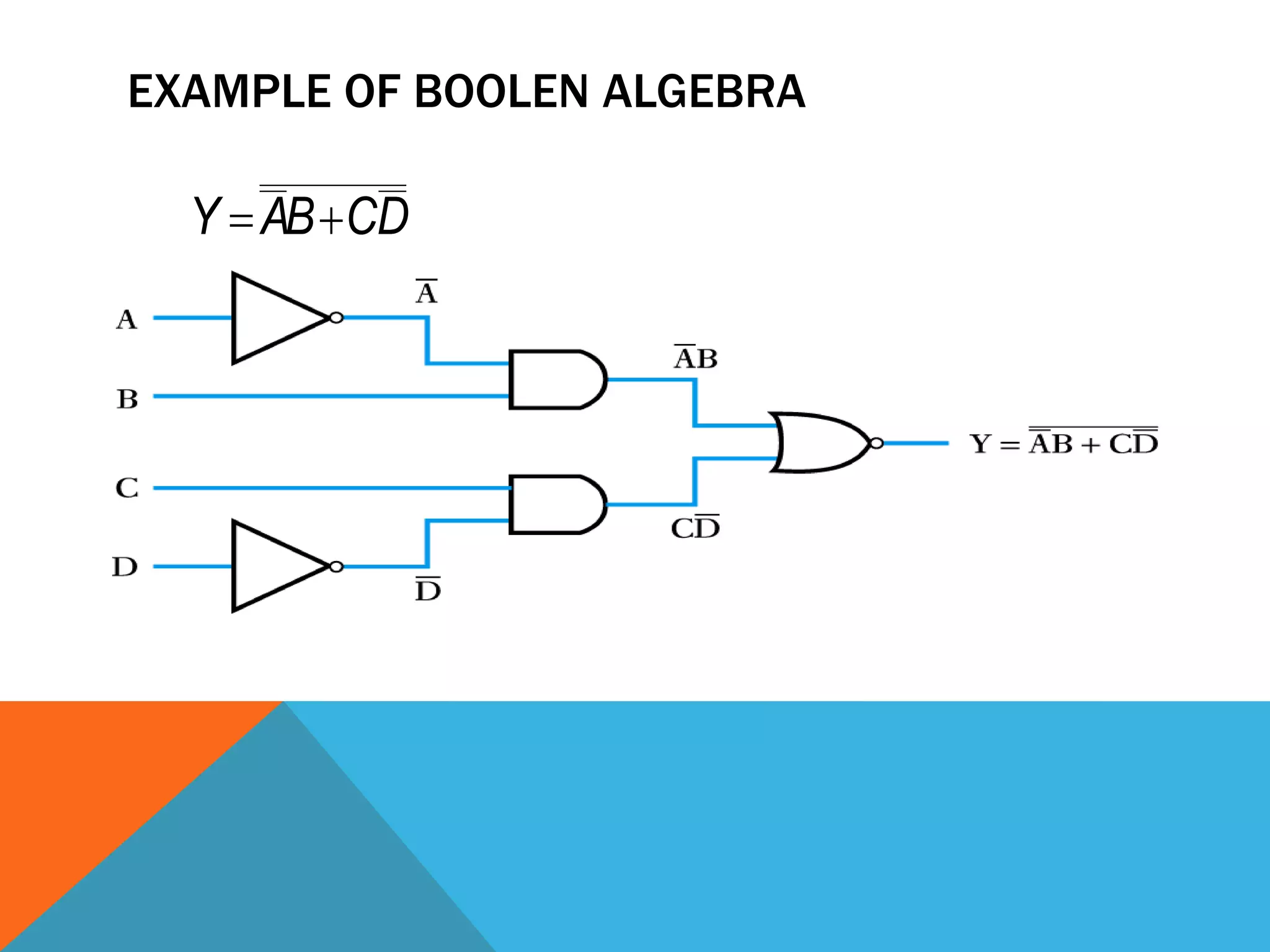
The document provides an introduction to logic gates and Boolean algebra. It discusses the different types of logic gates including NOT, AND, OR, NAND, NOR, XOR, and XNOR gates. Truth tables and logic circuit diagrams are presented as ways to represent the working of logic circuits. Boolean algebra rules are introduced as a way to simplify logic expressions without changing their functionality. Examples of Boolean algebra rules and their applications are also provided.

1. LOGIC GATES &
BOOLEN ALGEBRA
BY
M.VENKATESH

2. OUTLINE
 INTRODUCTION TO LOGIC GATES
 TYPES OF LOGIC GATES
 ADVANTAGES,DIADVANTAGES &
APLLICATIONS
 INTROUCTION TO BOOLEN ALGEBRA
 RULES OF BOOLEN ALGEBRA
 EXAMPLE FOR BOOLEN ALGEBRA

3. INTRODUCTION TO LOGIC GATES
 A logic gate is an elementary building block of a DIGITAL CIRCUIT
 Most logic gates have two inputs and one output.
 In most logic gates, the low state is approximately zero volts (0 V),
while the high state is approximately five volts positive (+5 V).
 binary conditions low for 0V or high for 1V
 There are three common ways in which to represent the working of a
logic circuit.
1. Truth Tables
2. Logic Circuit Diagram
3. Boolean Expression

4. LOGIC GATES
 A truth table is a chart of Boolean values (1s and 0s) arranged to
indicate the results (or outputs) of all possible inputs combinations.
 The lists of all possible inputs combination are arranged in columns
on the left and the resultant outputs are listed in columns on the right
side of the table.
 A logic circuit diagram uses the graphical representation or
description of logic gates in combination to represent a logic
expression.
 Boolean algebra can be used to write a logic expression in the form
of an equation.

5. TYPES OF LOGIC GATES

6. NOT GATE
 It Is also called as complementary or inversion gate.
 NOT gate perform the ‘~’ operation.
 It has one input and one output.

7. NOT GATE

8. NOT GATE APPLICATION
.

9. AND GATE
 It perform Multiplication operation.
 AND gate represented as ‘.’
 When both inputs are high then output will high

10. AND GATE

11. AND GATE APPLICATION

12. OR GATE
 It perform Addition operation.
 OR gate represented as ‘+’
 When both inputs are low then output will low

13. OR GATE

14. OR GATE APPLICATION
.

15. NAND GATE
 NAND gate Complement of AND gate.
 When both inputs are low then output will low

16. NAND GATE

17. NOR GATE
 NOR gate is Complement of OR gate
 When both inputs are low then output will be low

18. NOR GATE

19. EXCLUSIVE OR GATE
 It is also called as Athematic Gate
 When any one input is then output will high
 XOR gate is represented as 

20. XOR GATE

21. EXCLUSIVE NOR GATE
 XNOR gate is complement of XOR gate
 When both inputs are high or low then the output will high
 XNOR is represented as


22. XNOR GATE

23. ADVANTAGES
 The switching time is much faster than analog circuits.
 logic gates is less expensive
DISADVANTAGES
 Logic circuits uses more energy than other circuits like analog
circuits to accomplish the same tasks resultant circuit produces more
heat.
 For activation, logic circuits require power system i.e. portable or
battery power systems which are limited in power.

24. APPLICATIONS
 Personal Computers
 Mobile Phones
 Tablets
 Calculators and
 Digital Watches

25. BOOLEN ALGEBRA
 Boolen algebra is given by English Mathematician GEORGE
BOOLE
 It is set of rules used to simplify the given logic
expression without changing its functionality.
 It is used when number of variables are less.
GEORGE BOOLE
(1815-1864)

26. BOOLEN ALGEBRA
 Set of rules it is used to simply and minimize the equation.
 Logic Expression : F=A`B+BC+ABC ------(1)
---
F=A`B+BC ---------(2)
The above two functions are same
 To reduce the variable we use the map method or k-map method
 For (1) we required 5 logic gates
 For (2) we required 4 logic gates

27. BOOLEN ALGEBRA

28. RULES OF BOOLEN ALGEBRA
1. COMPLEMENT RULE
A COMPLEMENT=A` Or (NOT A) Or
A.(A`)`=A
2. AND RULE
A.A=A
A.1=A
A.0=0
A.A`=0
A

29. RULES
3. OR RULE
A+A=A
A+0=1
A+1=1
A+A`=1
4.DISTRUBTIVE LAW
A.(B+C) = A.B+A.C
A+(B.C) = (A+B).(A+C)

30. RULES
5. COMMULATATIVE LAW
A+B = B+A
A.B = B.A
6. ASSOCITATIVE LAW
(A.B).C =A.(B.C)
7. DEMORGANS LAW
(A+B)`=A`.B`
(A.B)`=A`+B`

31. EXAMPLE OF BOOLEN ALGEBRA
DCBAY 