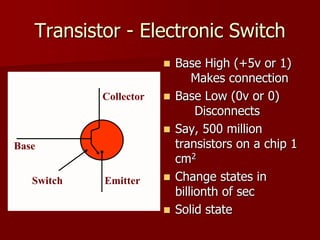
1) Transistors act as electronic switches that can be in either an "on" or "off" state, allowing circuits to perform logical operations. 2) Moore's Law predicts that the number of transistors on an integrated circuit will double about every two years. 3) Logic gates such as AND, OR, and NOT gates are electronic devices that take binary inputs and produce binary outputs according to their specific logical functions.

1. Computer Science 101
Logic Gates and Simple Circuits

2. Transistor - Electronic Switch

Collector


Base
Switch
Emitter


Base High (+5v or 1)
Makes connection
Base Low (0v or 0)
Disconnects
Say, 500 million
transistors on a chip 1
cm2
Change states in
billionth of sec
Solid state

3. Moore’s Law
In 1965, Intel co-founder Gordon
Moore saw the future. His prediction,
now popularly known as Moore's
Law, states that the number of
transistors on a chip doubles about
every two years.

4. Gates

A gate is an electronic device that takes
0/1 inputs and produces a 0/1 result.

5. NOT Gate

Output
Input

Input Low (0v or 0)
Output High (+5v or 1)

+5v
Input High (+5v or 1)
Output Low (0v or 0)
Output is opposite of
Input
NOT Gate
Ground
A
_
A

6. AND Gate

Output is 1 only if
• Input-1 is 1 and
• Input-2 is 1

+5v
Output
= Input1 AND Input2
Input-1
AND Gate
A
Input-2
B
Output
AB

7. OR Gate

• A is 1 or if
• B is 1
+5v

A
Output is 1 if
Output
= A OR B
B
OR Gate
A
Output
B
A+B

8. Boolean Expression

Python
Logical operators
• AND
• OR
• NOT
and (Python)
or (Python)
not (Python)

NOT ((x>y) AND ((x=5) OR (y=3))

not((x>y) and ((x==5)or(y==3)))

while (not((x>y) and ((x==5)or(y==3)))) :
…

9. Abstraction

In computer science, the term abstraction refers to
the practice of defining and using objects or
systems based on the high level functions they
provide.

We suppress the fine details of how these functions
are carried out or implemented.

In this way, we are able to focus on the big picture.

If the implementation changes, our high level work
is not affected.

10. Abstraction Examples

Boolean algebra - we can work with the
Boolean expressions knowing only the
properties or laws - we do not need to
know the details of what the variables
represent.

Gates - we can work with the logic gates
knowing only their function (output is 1
only if inputs are …). Don’t have to know
how gate is constructed from transistors.

11. Boolean Exp

Logic Circuit
To draw a circuit from a Boolean expression:
• From the left, make an input line for each variable.
• Next, put a NOT gate in for each variable that appears
negated in the expression.
• Still working from left to right, build up circuits for the
subexpressions, from simple to complex.

12. Logic Circuit: _ ____
AB+(A+B)B
Input Lines for Variables
A
B

13. Logic Circuit: _ ____
AB+(A+B)B
NOT Gate for B
A
B
_
B

14. Logic Circuit: _ ____
AB+(A+B)B
_
Subexpression AB
_
AB
A
B
_
B

15. Logic Circuit: _ ____
AB+(A+B)B
Subexpression A+B
_
AB
A
A+B
B
_
B

16. Logic Circuit: _ ____
AB+(A+B)B
___
Subexpression A+B
_
AB
A
A+B
B
_
B
____
A+B

17. Logic Circuit: _ ____
AB+(A+B)B
___
Subexpression (A+B)B
_
AB
A
A+B
B
_
B
____
A+B
____
(A+B)B

18. Logic Circuit: _ ____
AB+(A+B)B
Entire Expression
_
AB
A
A+B
B
_
B
____
A+B
____
(A+B)B

19. Logic Circuit
Boolean Exp

In the opposite direction, given a logic circuit, we
can write a Boolean expression for the circuit.

First we label each input line as a variable.

Then we move from the inputs labeling the
outputs from the gates.

As soon as the input lines to a gate are
labeled, we can label the output line.

The label on the circuit output is the result.

20. Logic Circuit
Boolean Exp
_
_ _
AB AB+AB
A
_
A
B
_
B
_
AB
A+B
Entire Expression
______
_ _
(AB+AB)(A+B)
______
_ _
AB+AB

21. Simplification Revisited

Once we have the BE for the
circuit, perhaps we can simplify.
AB
AB A
B
A B AB A
B
A
B A
B A
A
B A
BB
A
B A
AA
AB
BA
B

22. Logic Circuit
Reduces to:
Boolean Exp

23. The Boolean Triangle
Boolean
Expression
Logic
Circuit
Truth
Table

24. The Boolean Triangle
Boolean
Expression
Logic
Circuit
Truth
Table