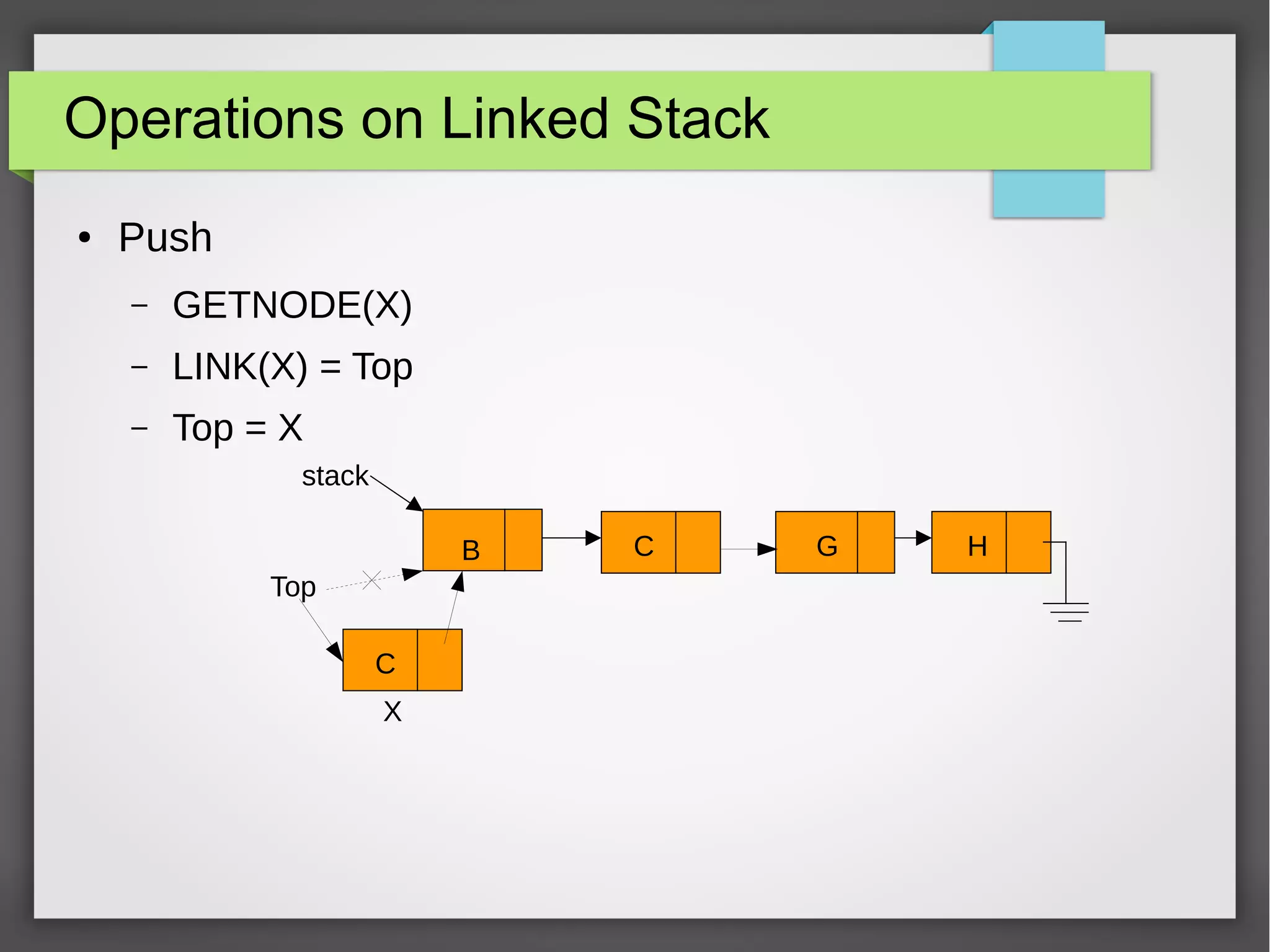
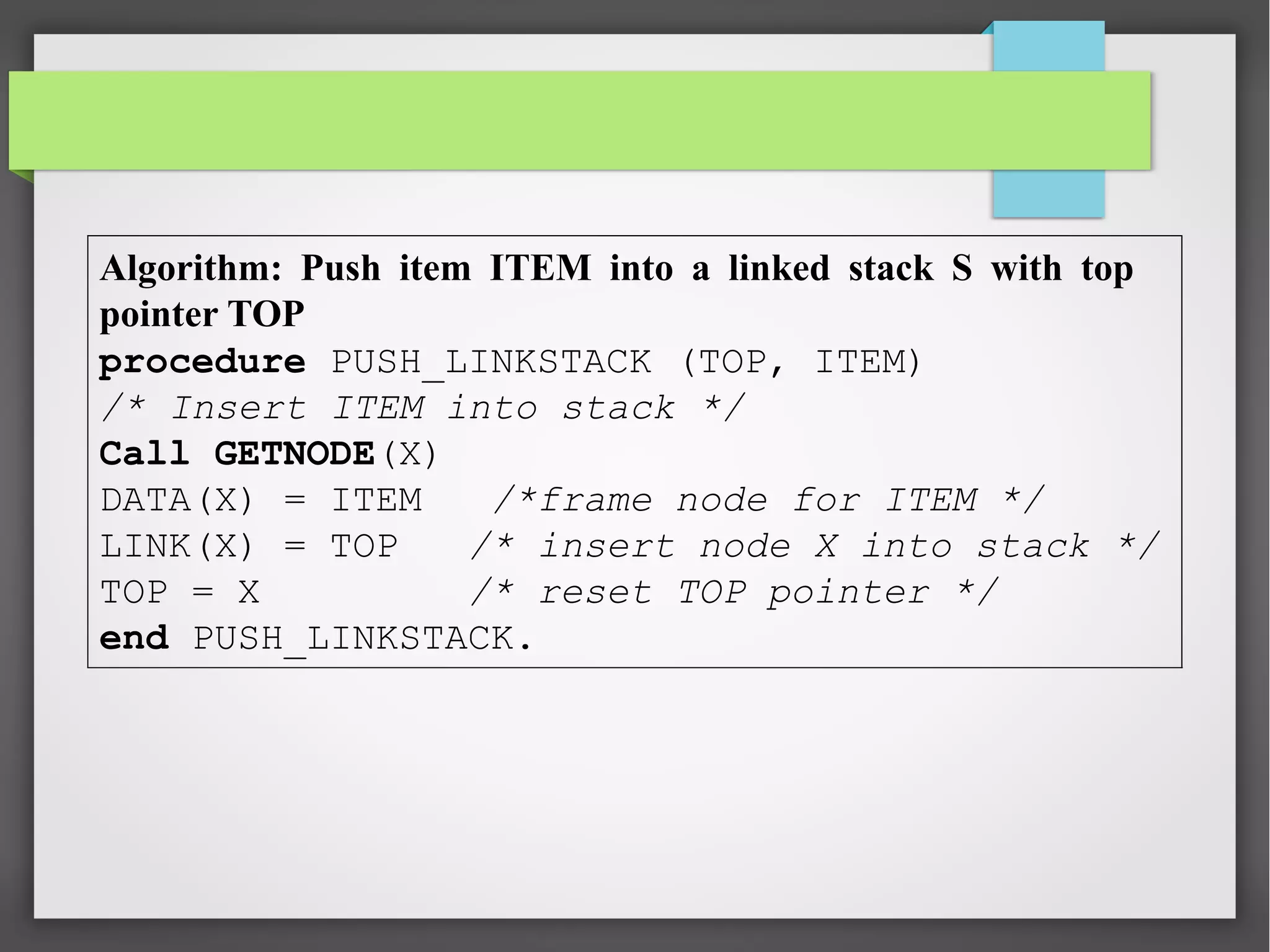
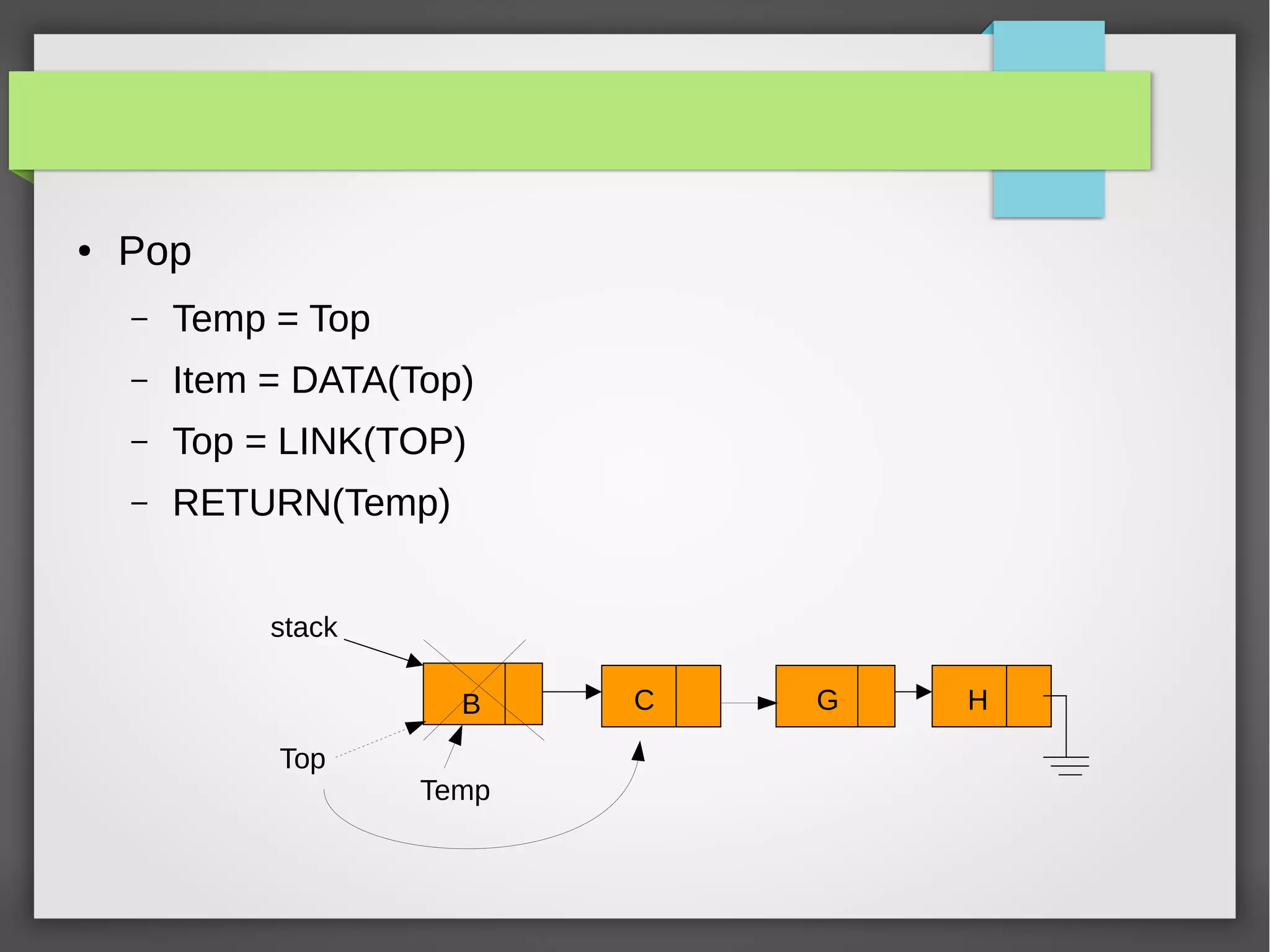
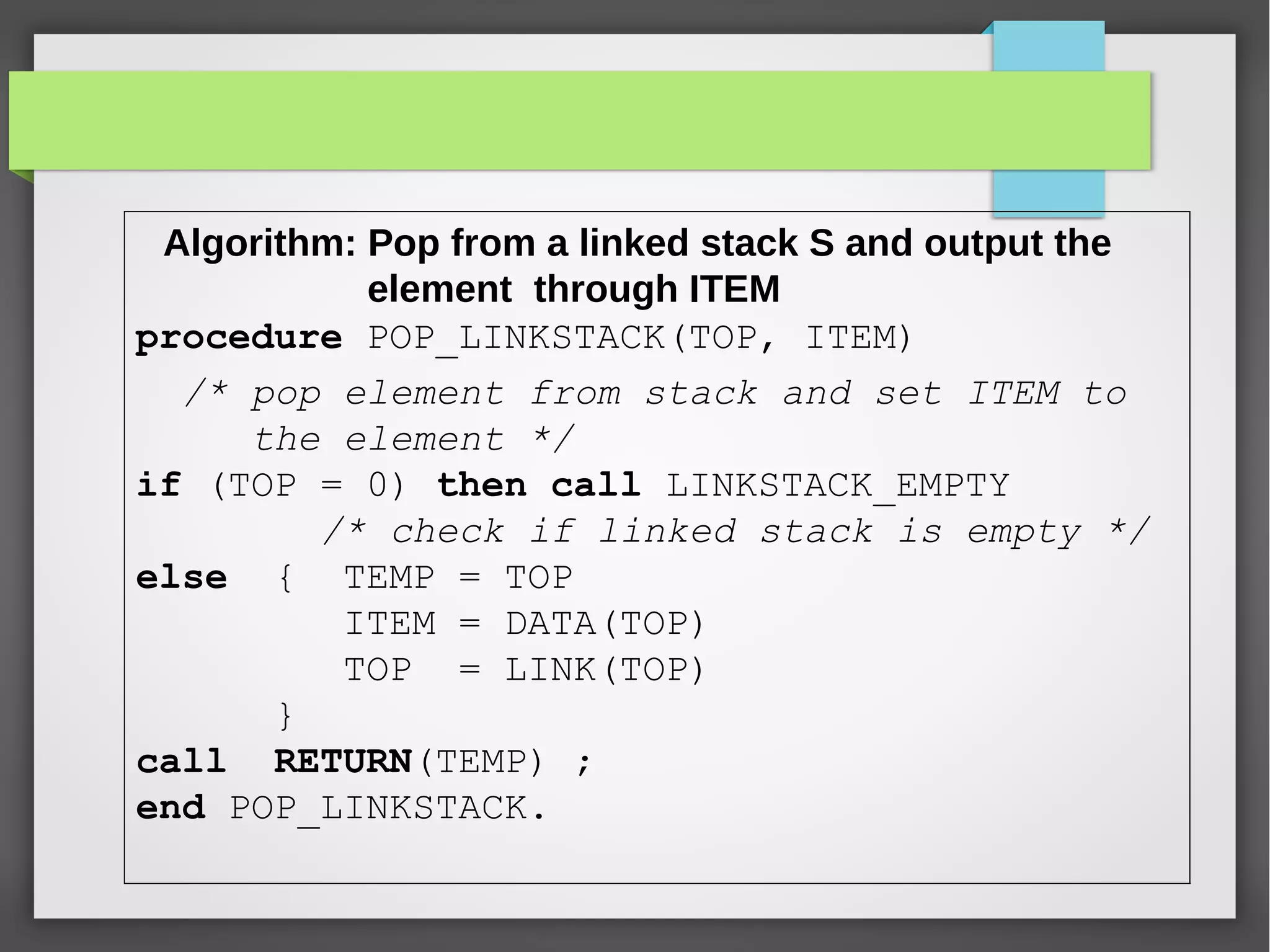
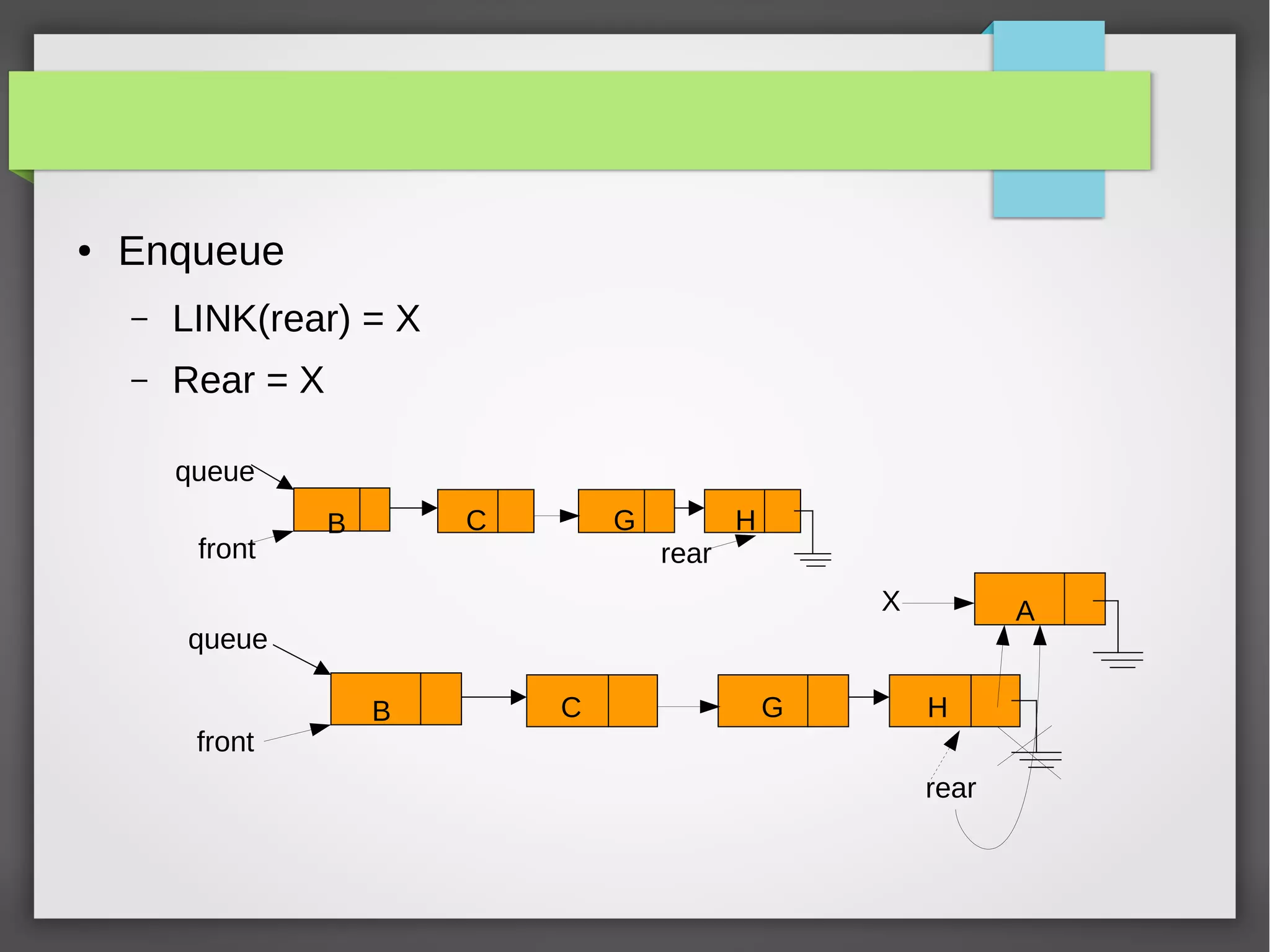
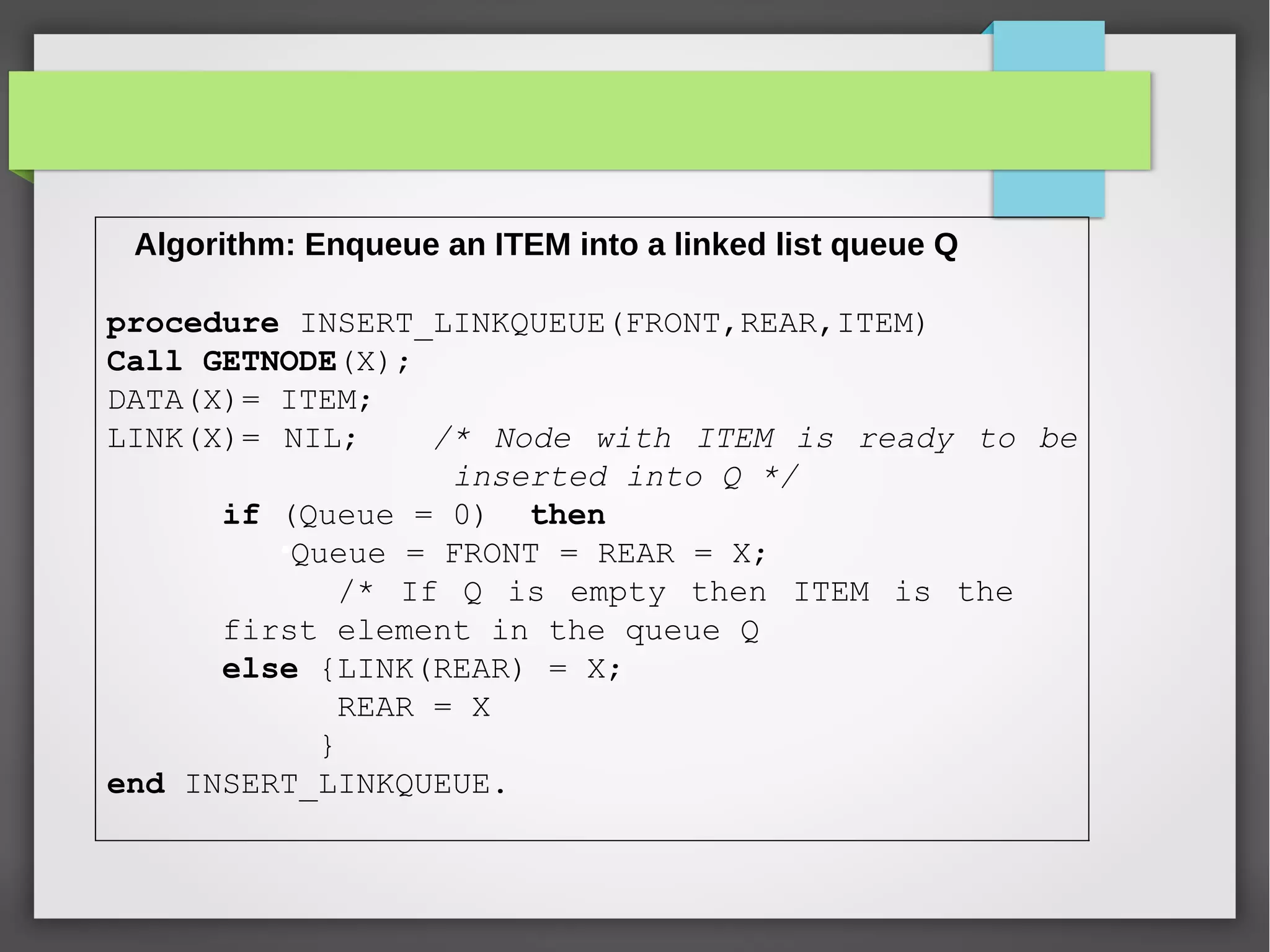
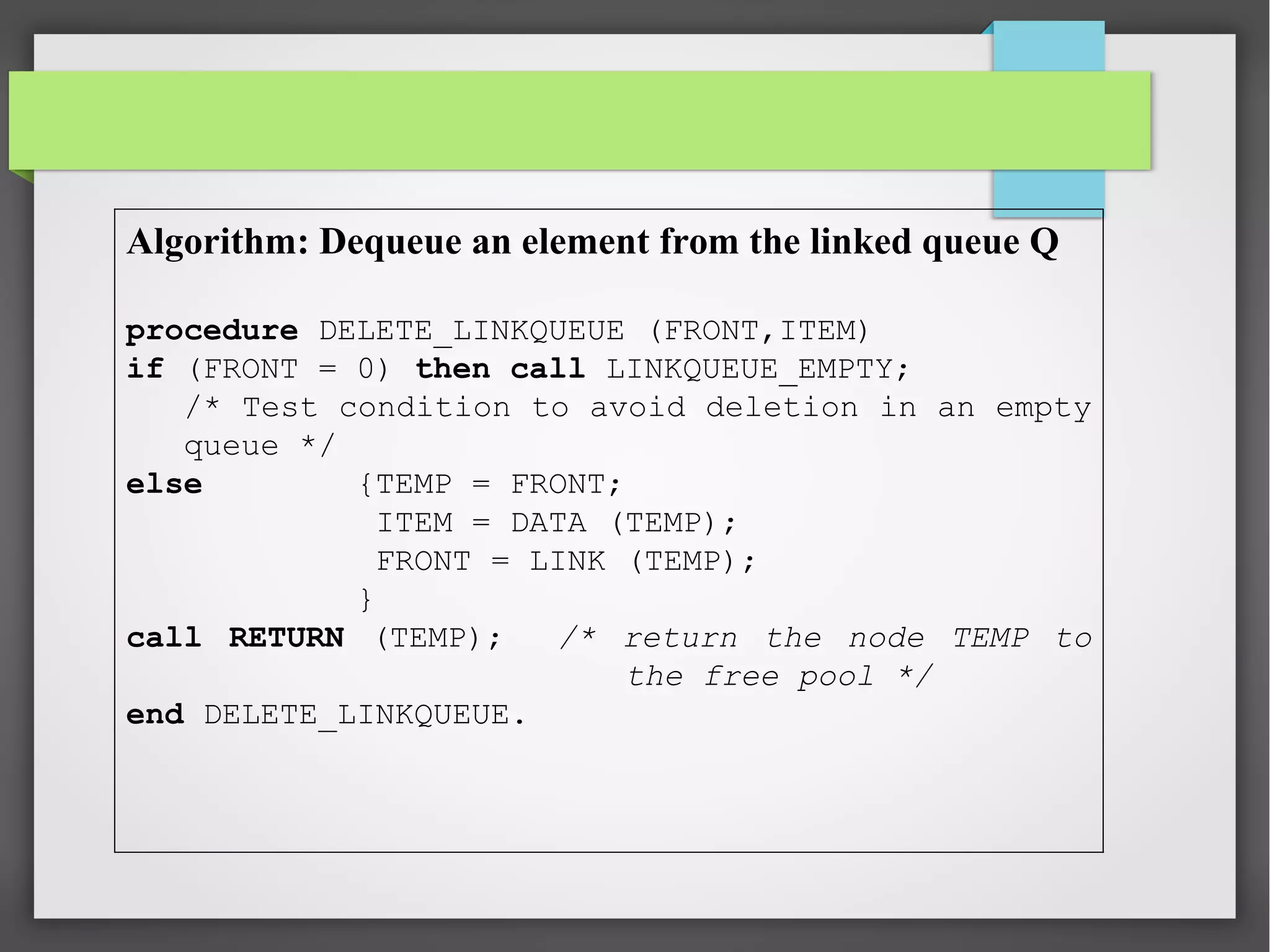
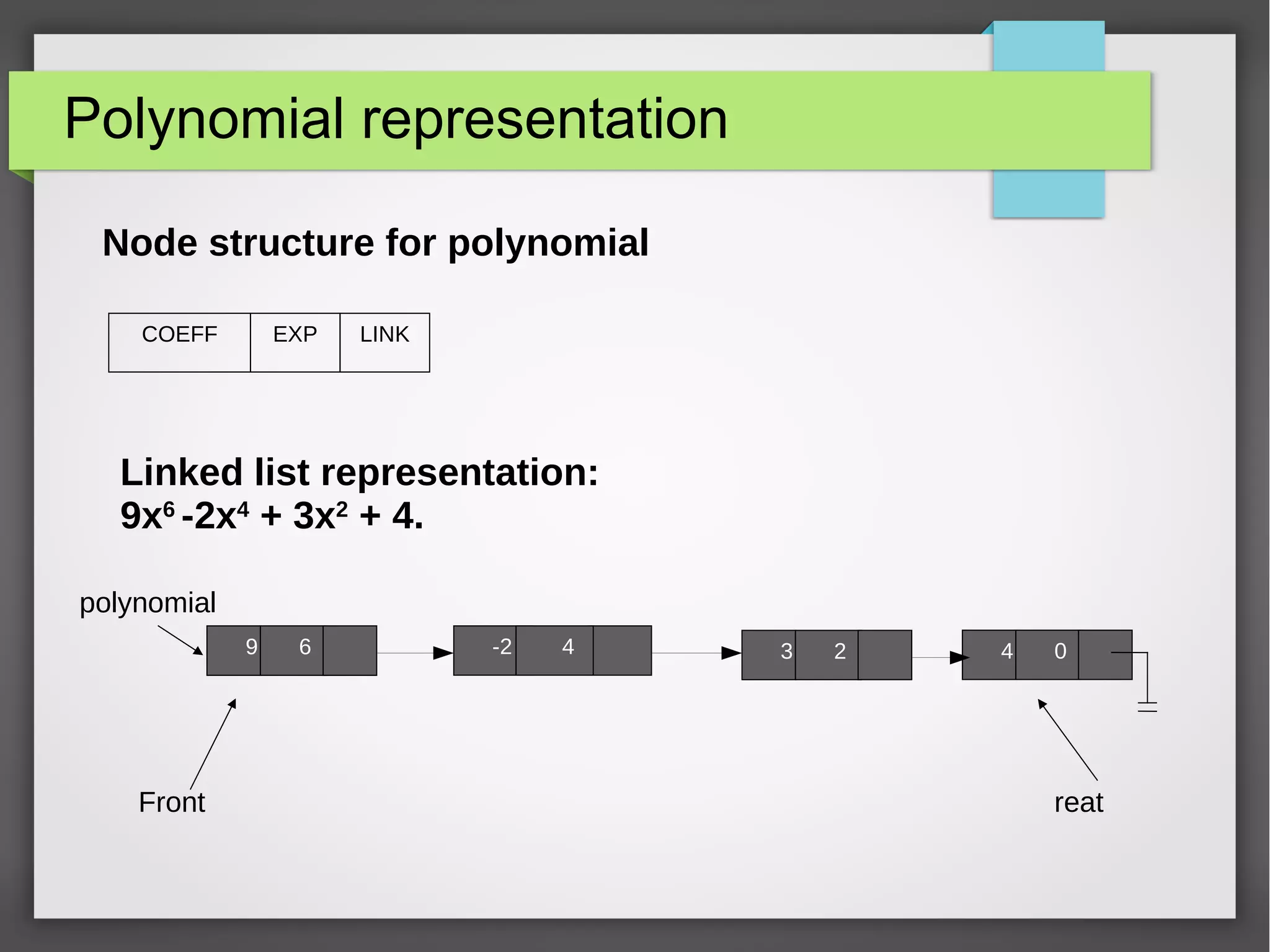
The document discusses linked stacks and linked queues. It provides an introduction to linked stacks and linked queues and how they are commonly implemented using singly linked lists. It then describes the key operations for each - push, pop, enqueue, and dequeue. Algorithms for each operation are presented using pseudocode. Examples of applications that can make use of linked stacks and queues are given, such as balancing symbols in an expression and representing polynomials.

1. Linked Stack and Linked Queue
Chapter 7

2. Outline
● Introduction
– Linked Stacks
– Linked Queues
● Operations on Linked Stacks and Linked Queues
– Linked Stack Operations
– Linked Queue Operations
– Algorithms for Push/Pop operations on a Linked Stack
– Algorithms for Insert/Delete operations in a Linked Queue
● Dynamic memory management and Linked Stacks
● Implementation of Linked Representations
● Applications
– Balancing Symbols
– Polynomial Representation

3. Introduction
● A linked stack is a linear list of elements commonly
implemented as a singly linked list whose start pointer
performs the role of the top pointer of a stack
● A linked queue is also a linear list of elements
commonly implemented as a singly linked list but with two
pointers viz., FRONT and REAR. The start pointer of the
singly linked list plays the role of FRONT while the pointer
to the last node is set to play the role of REAR.

4. Implementing Stack and Queue Using Linked List
6
1
2
3
4
5
A
B
E
D
G
F
Top = 6
1 2 3 4 5 6
B C
Front=1 Rear = 3
Stack[1:6] Queue[1:6]
B C G H
stack
Top
B C G H
queue
front rear

5. Operations of Linked Stack and
Linked Queue

6. Operations on Linked Stack
● Push
– GETNODE(X)
– LINK(X) = Top
– Top = X
B C G H
stack
Top
C
X

7. Algorithm: Push item ITEM into a linked stack S with top
pointer TOP
procedure PUSH_LINKSTACK (TOP, ITEM)
/* Insert ITEM into stack */
Call GETNODE(X)
DATA(X) = ITEM /*frame node for ITEM */
LINK(X) = TOP /* insert node X into stack */
TOP = X /* reset TOP pointer */
end PUSH_LINKSTACK.

8. ● Pop
– Temp = Top
– Item = DATA(Top)
– Top = LINK(TOP)
– RETURN(Temp)
B C G H
stack
Top
Temp

9. Algorithm: Pop from a linked stack S and output the
element through ITEM
procedure POP_LINKSTACK(TOP, ITEM)
/* pop element from stack and set ITEM to
the element */
if (TOP = 0) then call LINKSTACK_EMPTY
/* check if linked stack is empty */
else { TEMP = TOP
ITEM = DATA(TOP)
TOP = LINK(TOP)
}
call RETURN(TEMP) ;
end POP_LINKSTACK.

10. ● Enqueue
– LINK(rear) = X
– Rear = X
B C G H
queue
front
rear
A
X
B C G H
queue
front rear

11. Algorithm: Enqueue an ITEM into a linked list queue Q
procedure INSERT_LINKQUEUE(FRONT,REAR,ITEM)
Call GETNODE(X);
DATA(X)= ITEM;
LINK(X)= NIL; /* Node with ITEM is ready to be
inserted into Q */
if (Queue = 0) then
•Queue = FRONT = REAR = X;
/* If Q is empty then ITEM is the
first element in the queue Q
else {LINK(REAR) = X;
REAR = X
}
end INSERT_LINKQUEUE.

12. ● Dequeue
– Temp = front
– front = Link(front)
– Item = DATA(Temp)
– RETURN(Temp)
B C G H
queue
front rear
Temp

13. Algorithm: Dequeue an element from the linked queue Q
procedure DELETE_LINKQUEUE (FRONT,ITEM)
if (FRONT = 0) then call LINKQUEUE_EMPTY;
/* Test condition to avoid deletion in an empty
queue */
else {TEMP = FRONT;
ITEM = DATA (TEMP);
FRONT = LINK (TEMP);
}
call RETURN (TEMP); /* return the node TEMP to
the free pool */
end DELETE_LINKQUEUE.

14. Implementing Linked list Queue and stack
● Balancing Symbols
● Polynomial representation

15. Balancing symbols
Algorithm: To check for the balancing of parentheses in a string
procedure BALANCE_ EXPR(E)
/*E is the expression padded with a $ to indicateend of input*/
clear stack;
while not end_of_string(E)
read character; /* read a character from string E*/
if character == '{' //is an open symbol
then push character in to stack;
if character = '}' //is a close symbol
then
if stack is empty then ERROR ()
else {pop the stack;
if character != popped character
then ERROR();
}
endwhile
if stack not empty then ERROR();
end BALANCE_EXPR.

16. Polynomial representation
COEFF EXP LINK
9 6 3 2 4 0
-2 4
Node structure for polynomial
Linked list representation:
9x6
-2x4
+ 3x2
+ 4.
polynomial
Front reat