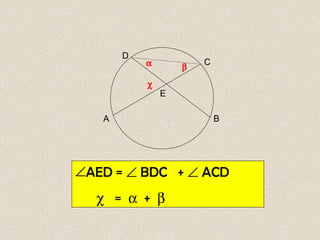
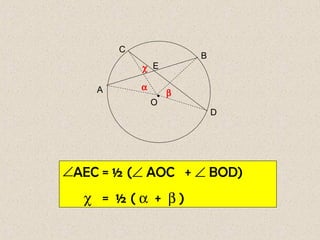
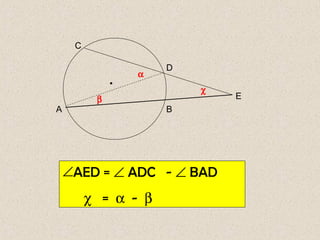
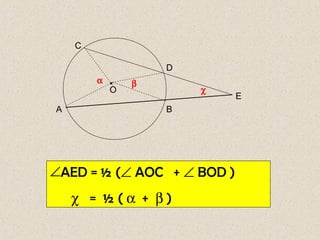
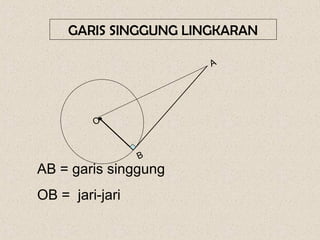
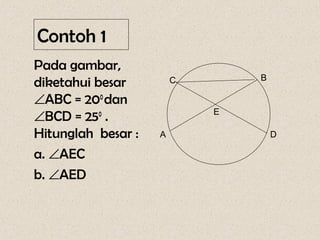
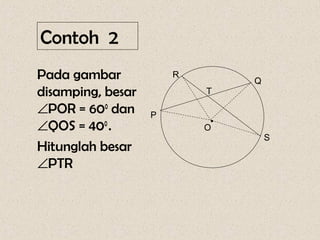
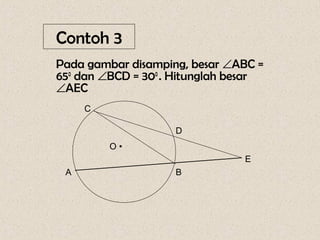
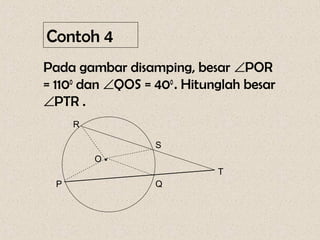
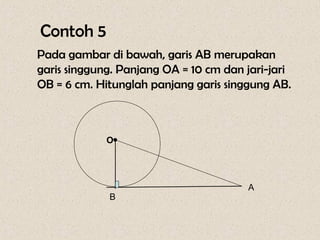
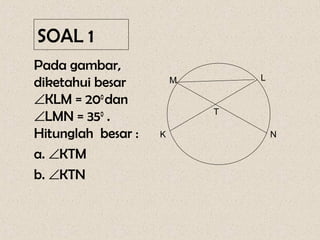
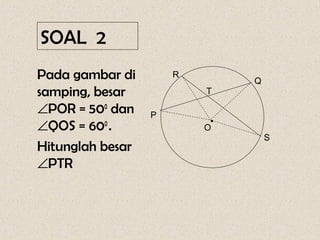
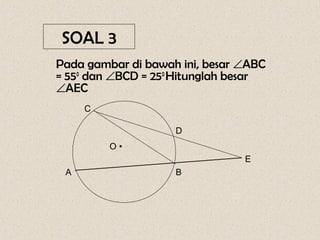
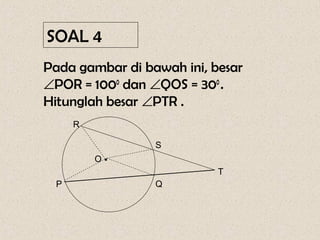
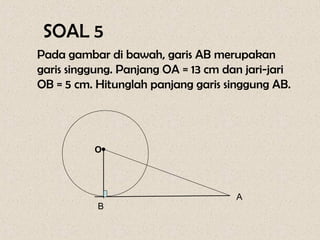
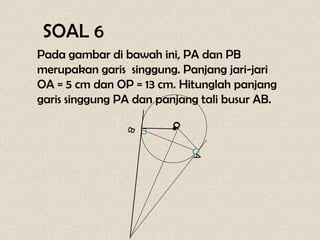
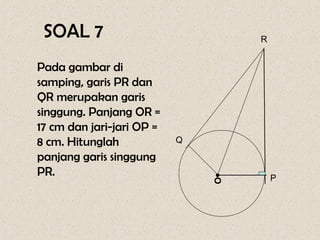
Dokumen ini membahas mengenai sudut yang dibentuk oleh dua tali busur dan garis singgung dalam lingkaran, serta cara menghitungnya. Terdapat beberapa contoh soal yang menunjukkan penerapan rumus-rumus untuk menghitung sudut dan panjang garis singgung. Penjelasan mencakup sudut yang terbentuk di dalam dan di luar lingkaran, serta penerapan teorema Pythagoras dalam menghitung panjang garis singgung.

2. LINGKARAN

3. Materi :
• Sudut antara dua tali busur
• Sudut antara dua tali busur
yang berpotongan di luar
lingkaran
• Garis singgung lingkaran

4. Sudut antara dua tali busur
1. Sudut antara dua tali busur yang
berpotongan dalam lingkaran.
Besar sudut yang dibentuk oleh dua
tali busur yang berpotongan di
dalam lingkaran sama dengan
jumlah sudut keliling yang
menghadap busur yang terletak di
antara kaki-kaki sudutnya.

5. D
α β
C
χ
E
A B
∠AED = ∠ BDC + ∠ ACD
χ = α + β

6. atau :
Besar sudut ayang dibentuk oleh
dua tali busur yang berpotongan
do dalam lingkaran , sama
dengan ½ jumlah sudut pusat
yang menghadap busur yang
terletak di antara kaki-kaki
sudutnya.

7. C
B
χ E
A α
• β
O
D
∠AEC = ½ (∠ AOC + ∠ BOD)
χ = ½(α + β)

8. Sudut antara dua tali busur
2. Jika dua tali busur yang
berpotongan di luar lingkaran,
maka :
Besar sudut yang terjadi sama
dengan jselisih sudut pusat yang
menghadap busur yang terletak
di antara kaki-kaki sudutnya.

9. C
D
α
•
χ
β E
A B
∠AED = ∠ ADC - ∠ BAD
χ = α - β

10. atau :
Jika dua tali busur yang
berpotongan di luar lingkaran,
maka :
Besar sudut yang terjadi sama
dengan ½ selisih sudut pusat yang
menghadap busur yang terletak
di antara kaki-kaki sudutnya.

11. C
D
α • β
O χ
E
A B
∠AED = ½ (∠ AOC + ∠ BOD )
χ = ½(α + β)

12. GARIS SINGGUNG LINGKARAN
A
O•
B
AB = garis singgung
OB = jari-jari

13. Contoh 1
Pada gambar,
B
diketahui besar C
∠ABC = 200 dan
∠BCD = 250 . E
Hitunglah besar : A D
a. ∠AEC
b. ∠AED

14. Pembahasan :
∠ABC = 200
∠BCD = 250
a. ∠AEC = ∠ABC + ∠BCD
= 200 + 250
= 450
b. ∠AED = 1800 - ∠AEC
= 1800 - 450
= 1350

15. Contoh 2
Pada gambar R
Q
disamping, besar T
∠POR = 600 dan P
∠QOS = 400 . O
•
S
Hitunglah besar
∠PTR

16. Pembahasan :
∠POR = 600
∠QOS = 400
a. ∠PTR = ½ ( ∠POR + ∠QOS)
= ½ (600 + 400 )
= ½ x 1000
= 500
Jadi, besar ∠PTR = 500

17. Contoh 3
Pada gambar disamping, besar ∠ABC =
650 dan ∠BCD = 300 . Hitunglah besar
∠AEC
C
D
O•
E
A B

18. Pembahasan :
∠ABC = 650
∠BCD = 300
∠AEC = ∠ABC - ∠BCD
= 650 - 350
= 250
Jadi, besar ∠AEC = 250

19. Contoh 4
Pada gambar disamping, besar ∠POR
= 1100 dan ∠QOS = 400 . Hitunglah besar
∠PTR .
R
S
O•
T
P Q

20. Pembahasan :
∠POR = 1100
∠QOS = 400
∠PTR = ½ (∠POR - ∠QOS)
= ½ ( 1100 - 400 )
= 350
Jadi, besar ∠PTR = 350

21. Contoh 5
Pada gambar di bawah, garis AB merupakan
garis singgung. Panjang OA = 10 cm dan jari-jari
OB = 6 cm. Hitunglah panjang garis singgung AB.
O•
A
B

22. Pembahasan :
Perhatikan Δ OAB siku-siku di titik B
AB2 = OA2 - OB2
= 102 - 62
= 100 - 36
= 64
AB = √ 64 = 8 cm.
Jadi, panjang garis singgung AB = 8 cm.

24. SOAL 1
Pada gambar,
L
diketahui besar M
∠KLM = 200 dan
∠LMN = 350 . T
Hitunglah besar : K N
a. ∠KTM
b. ∠KTN

25. Pembahasan :
∠KLM = 200
∠LMN = 350
a. ∠KTM = ∠KLM + ∠LMN
= 200 + 350
= 550
b. ∠KTN = 1800 - ∠KTM
= 1800 - 550
= 1250

26. SOAL 2
Pada gambar di R
Q
samping, besar T
∠POR = 500 dan P
∠QOS = 600 . O
•
S
Hitunglah besar
∠PTR

27. Pembahasan :
∠POR = 500
∠QOS = 600
a. ∠PTR = ½ ( ∠POR + ∠QOS)
= ½ (500 + 600 )
= ½ x 1100
= 550
Jadi, besar ∠PTR = 550

28. SOAL 3
Pada gambar di bawah ini, besar ∠ABC
= 550 dan ∠BCD = 250 Hitunglah besar
∠AEC
C
D
O•
E
A B

29. Pembahasan :
∠ABC = 550
∠BCD = 250
∠AEC = ∠ABC - ∠BCD
= 550 - 250
= 300
Jadi, besar ∠AEC = 300

30. SOAL 4
Pada gambar di bawah ini, besar
∠POR = 1000 dan ∠QOS = 300 .
Hitunglah besar ∠PTR .
R
S
O•
T
P Q

31. Pembahasan :
∠POR = 1000
∠QOS = 300
∠PTR = ½ (∠POR - ∠QOS)
= ½ ( 1000 - 300 )
= 350
Jadi, besar ∠PTR = 350

32. SOAL 5
Pada gambar di bawah, garis AB merupakan
garis singgung. Panjang OA = 13 cm dan jari-jari
OB = 5 cm. Hitunglah panjang garis singgung AB.
O •
A
B

33. Pembahasan :
Perhatikan Δ OAB siku-siku di titik B
AB2 = OA2 - OB2
= 132 - 52
= 169 - 25
= 144
AB = √ 144 = 12 cm.
Jadi, panjang garis singgung AB = 12 cm.

34. SOAL 6
Pada gambar di bawah ini, PA dan PB
merupakan garis singgung. Panjang jari-jari
OA = 5 cm dan OP = 13 cm. Hitunglah panjang
garis singgung PA dan panjang tali busur AB.
•O
B
A

35. Pembahasan :
OA = 5 cm dan OP = 13 cm.
∆ AOP siku-siku di titik A
PA2 = OP2 - OA2
= 132 - 52
= 169 – 25
= 144
PA = √ 144 = 12
Jadi, panjang garis singgung PA= 12 cm.

36. Luas layang-layang OAPB
L. OAPB = ½ x OP x AB
2( ½ x 12 x 5) = ½ x 13 x AB
120 = 13 AB
AB = 120 : 13
= 9,23
Jadi, panjang tali busur AB = 9,23 cm.

37. SOAL 7 R
Pada gambar di
samping, garis PR dan
QR merupakan garis
singgung. Panjang OR =
17 cm dan jari-jari OP =
8 cm. Hitunglah Q
panjang garis singgung
PR.
•
P
O

38. Pembahasan :
OP = 8 cm dan OR = 17 cm.
∆ POR siku-siku di titik P
PR2 = OR2 - OP2
= 172 - 82
= 289 – 64
= 225
PA = √ 225 = 15
Jadi, panjang garis singgung PR= 15 cm.