Uploaded byLS Instruments
Light Scattering Fundamentals (2019 Logo)
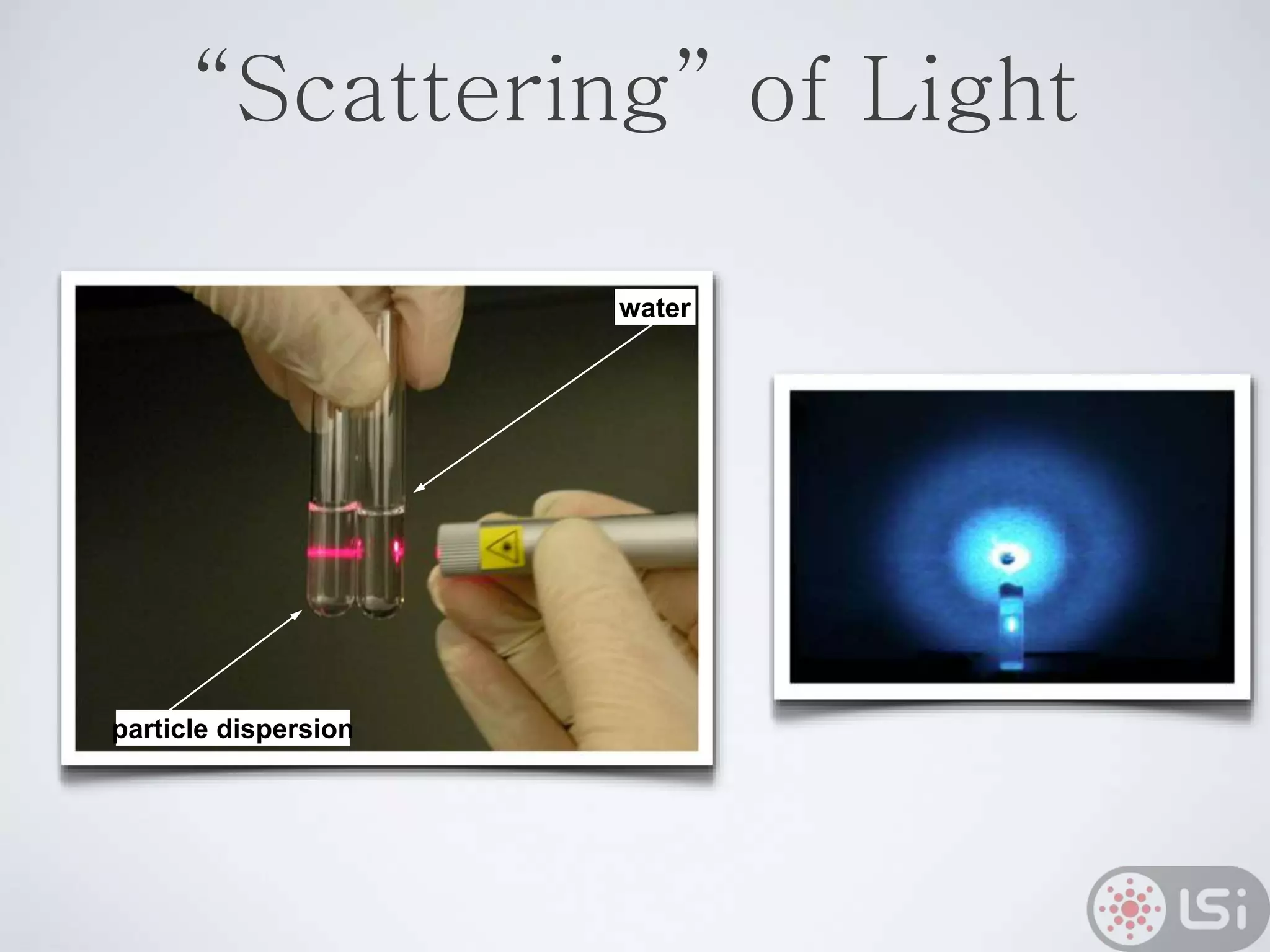
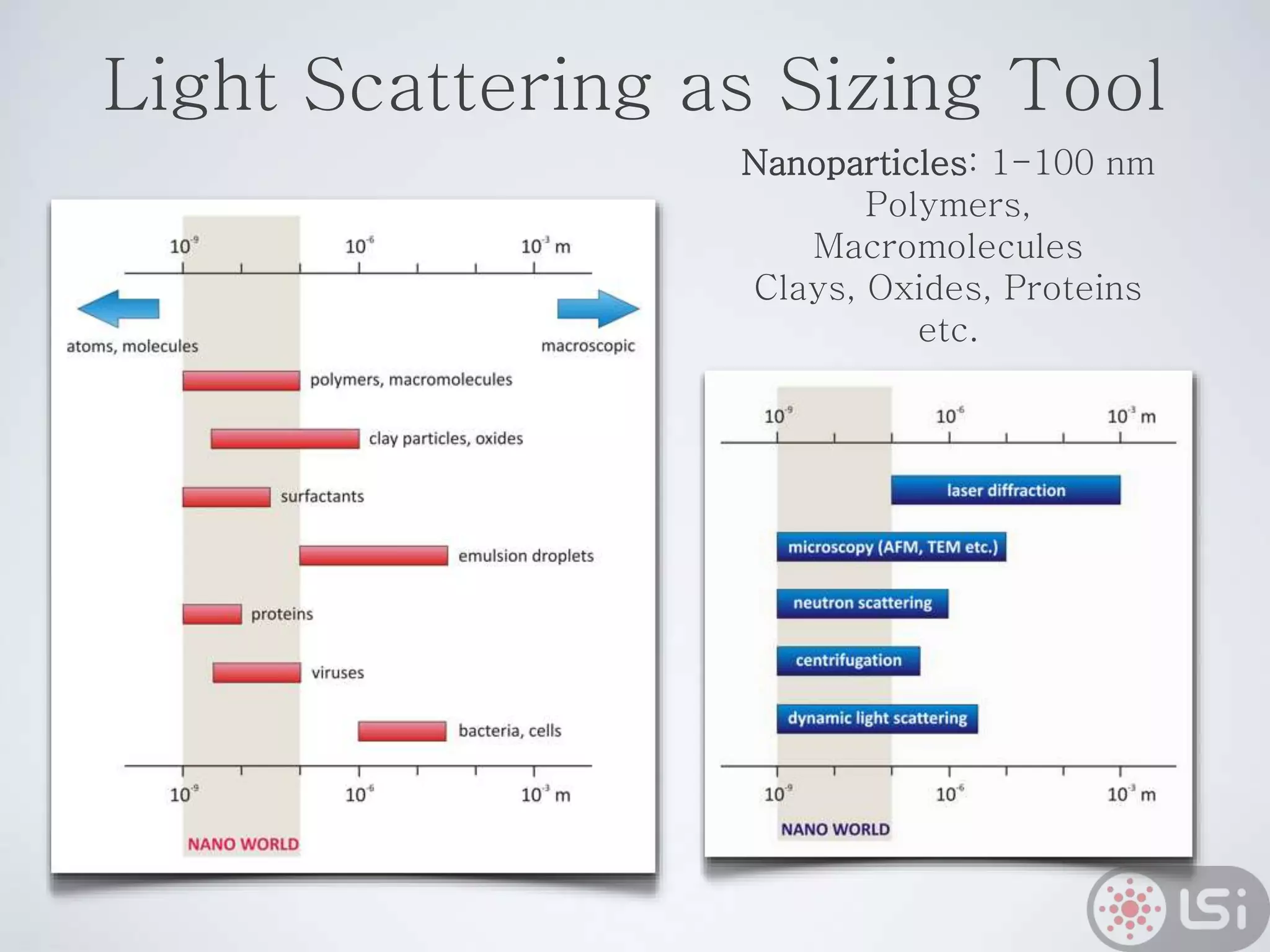
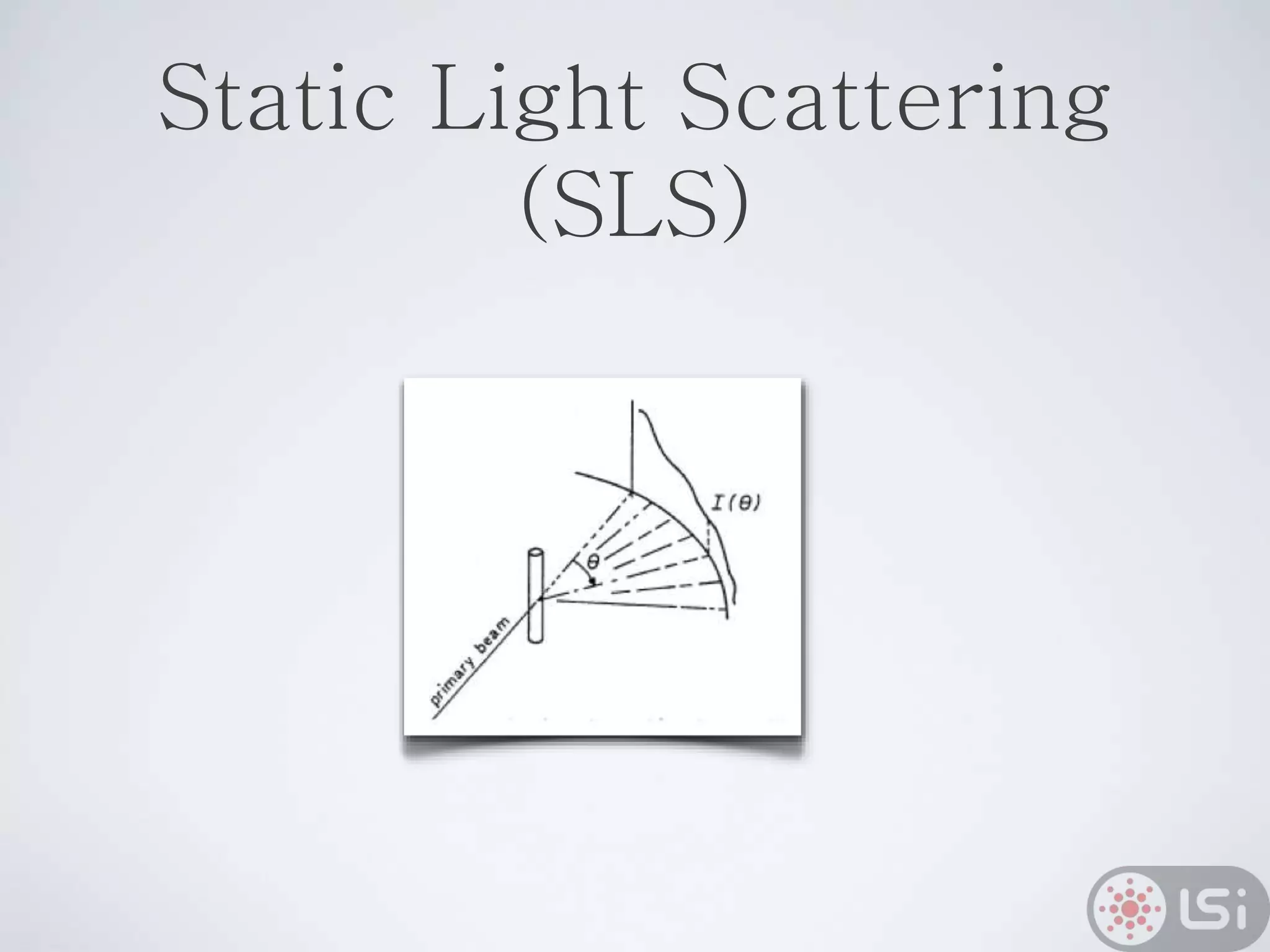
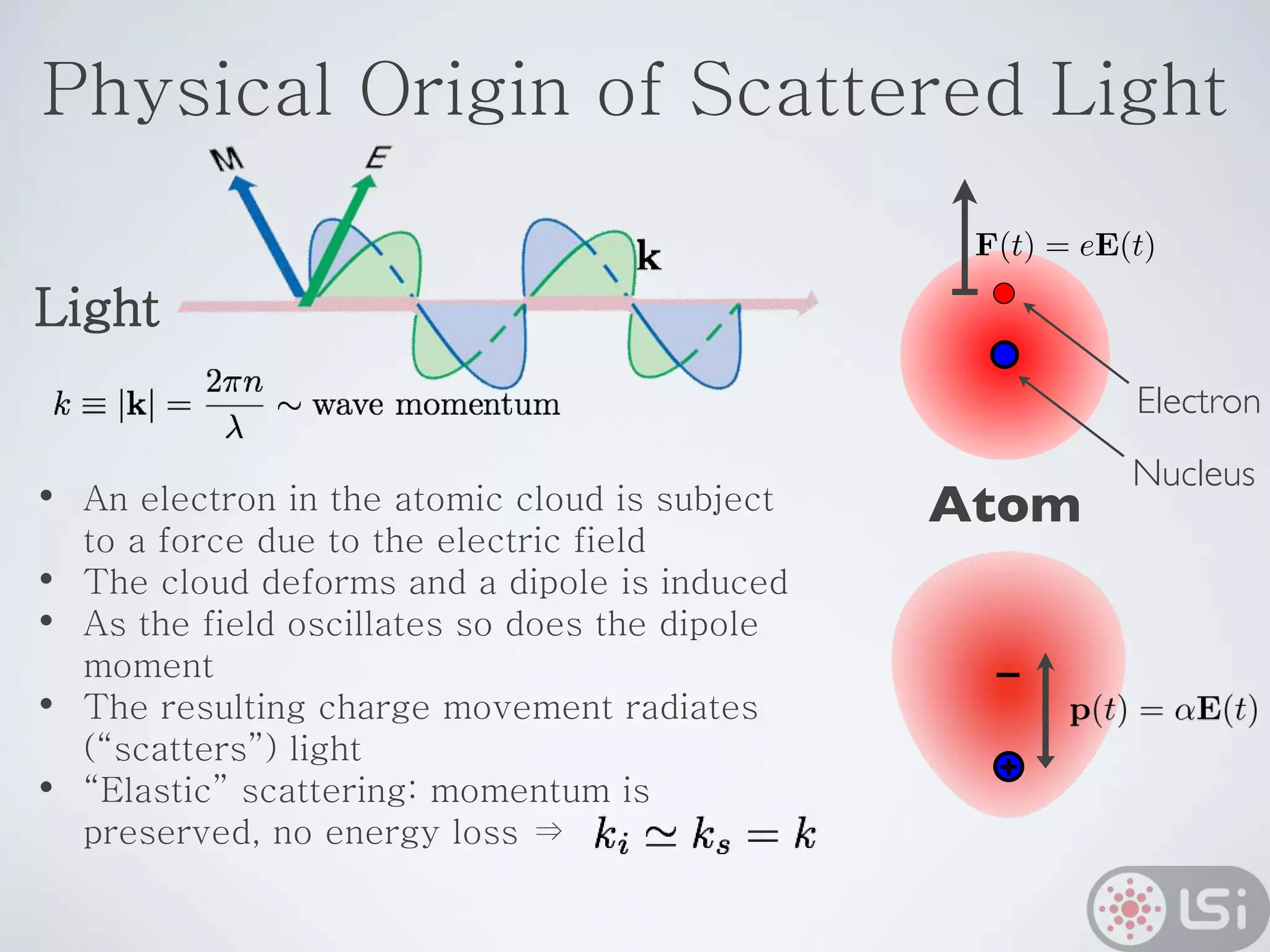
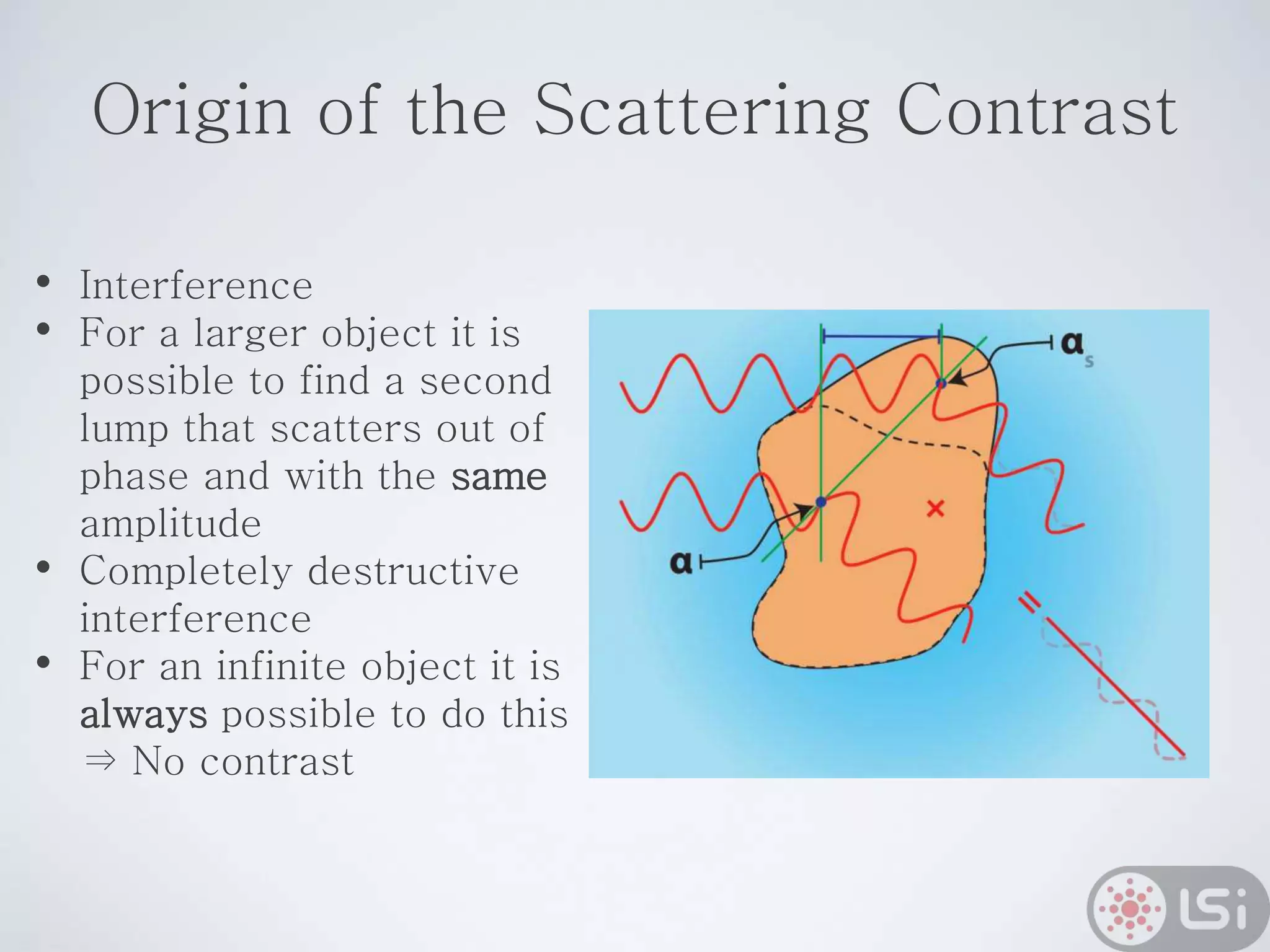
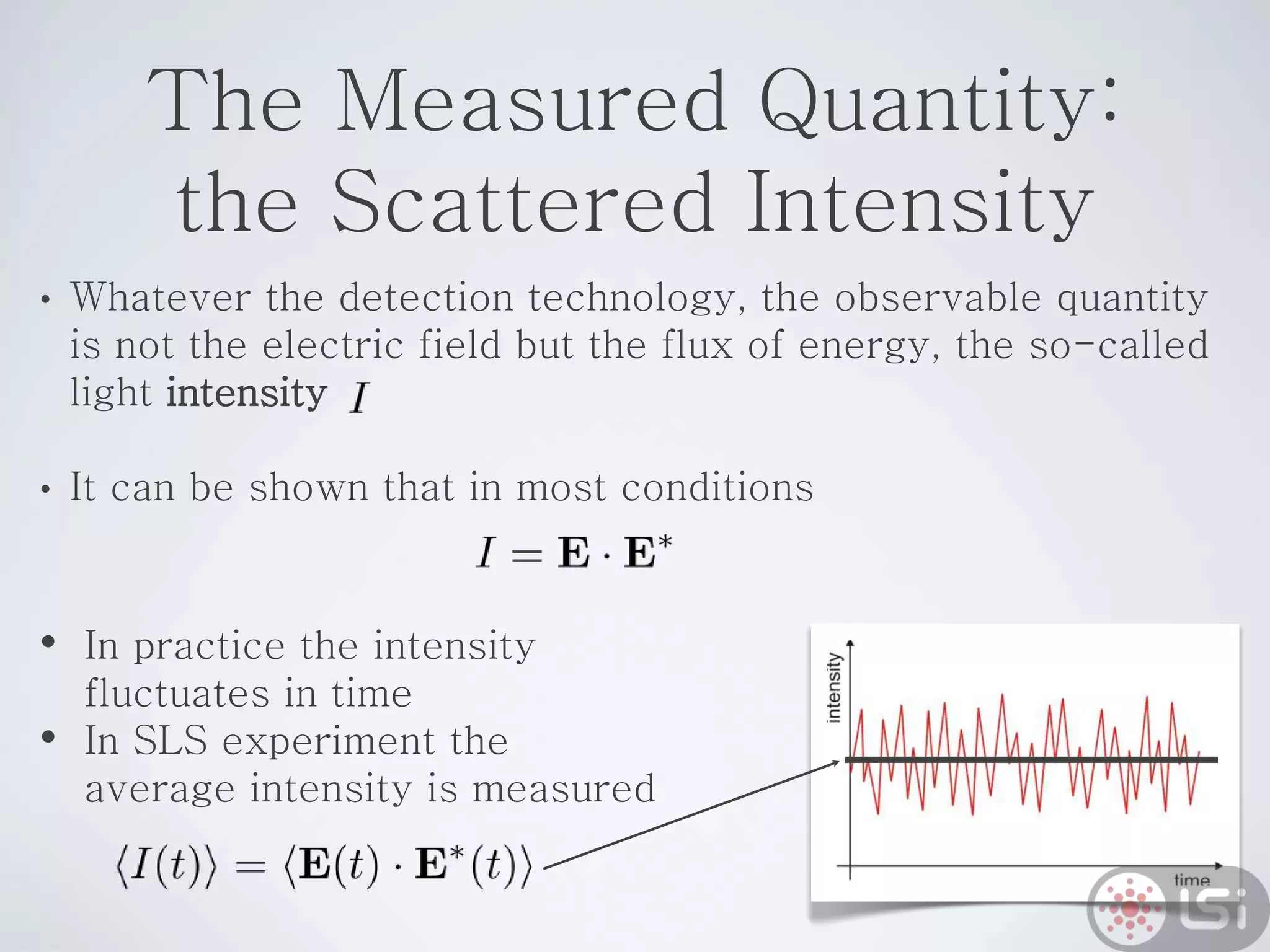
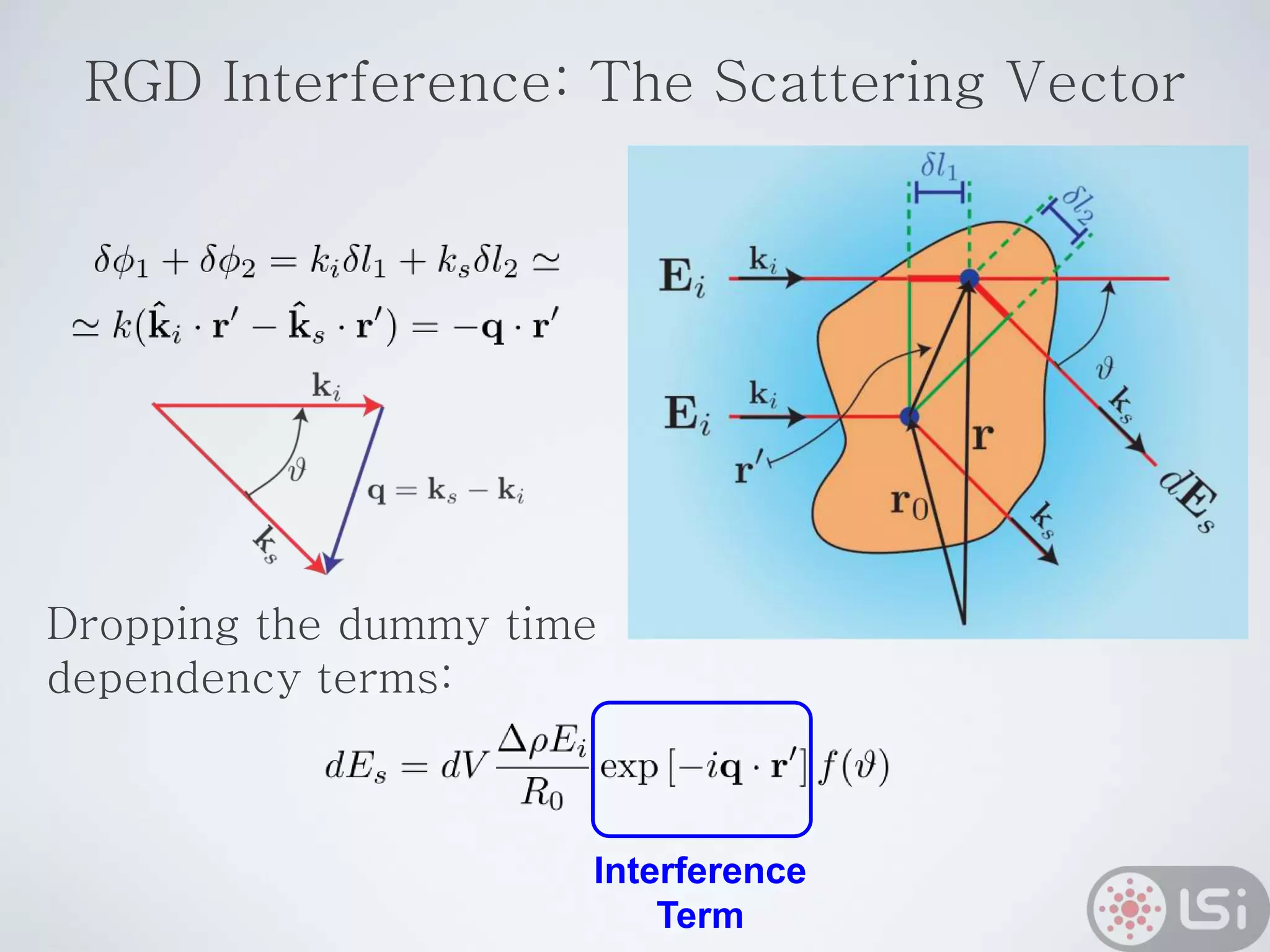
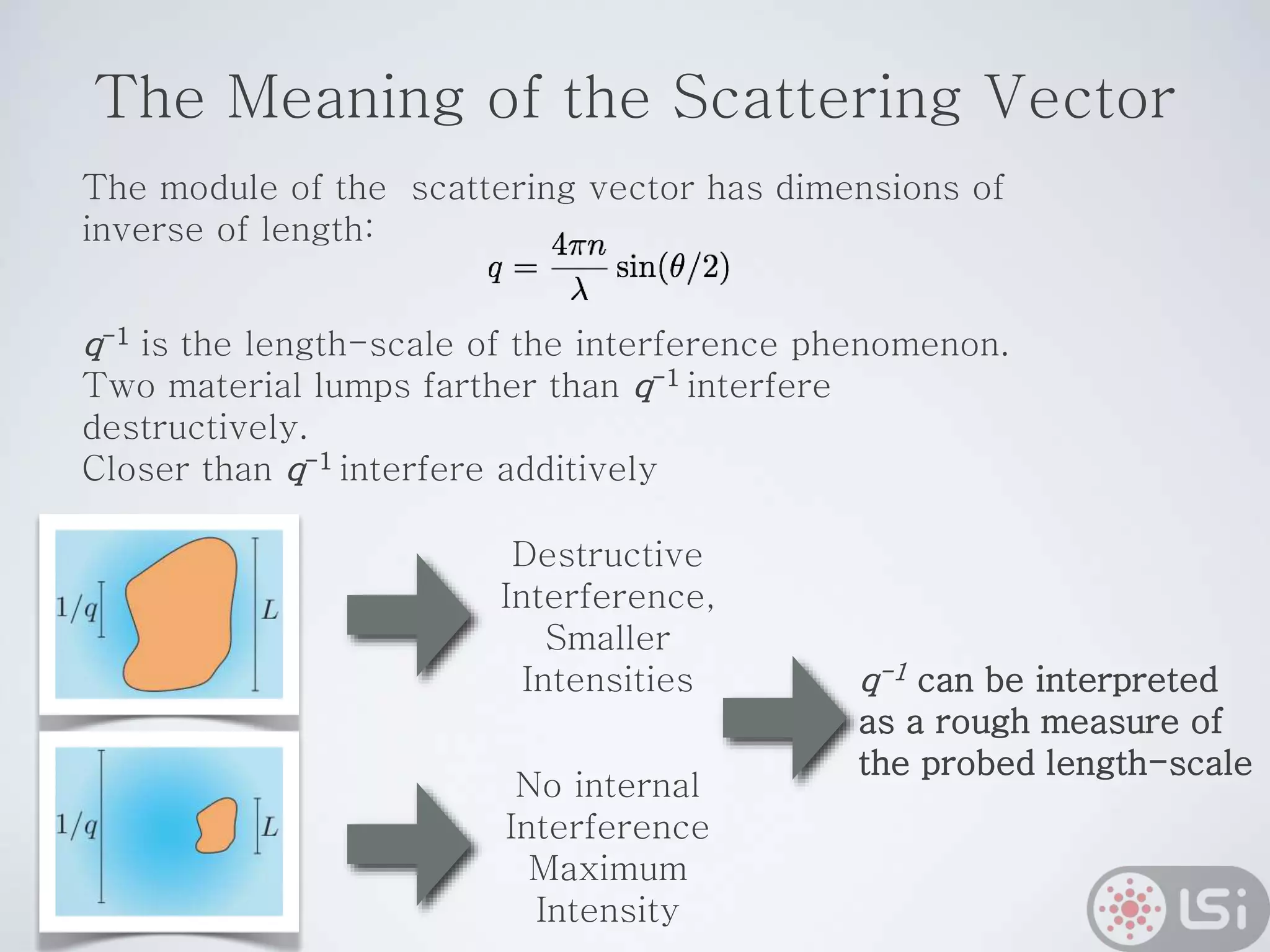
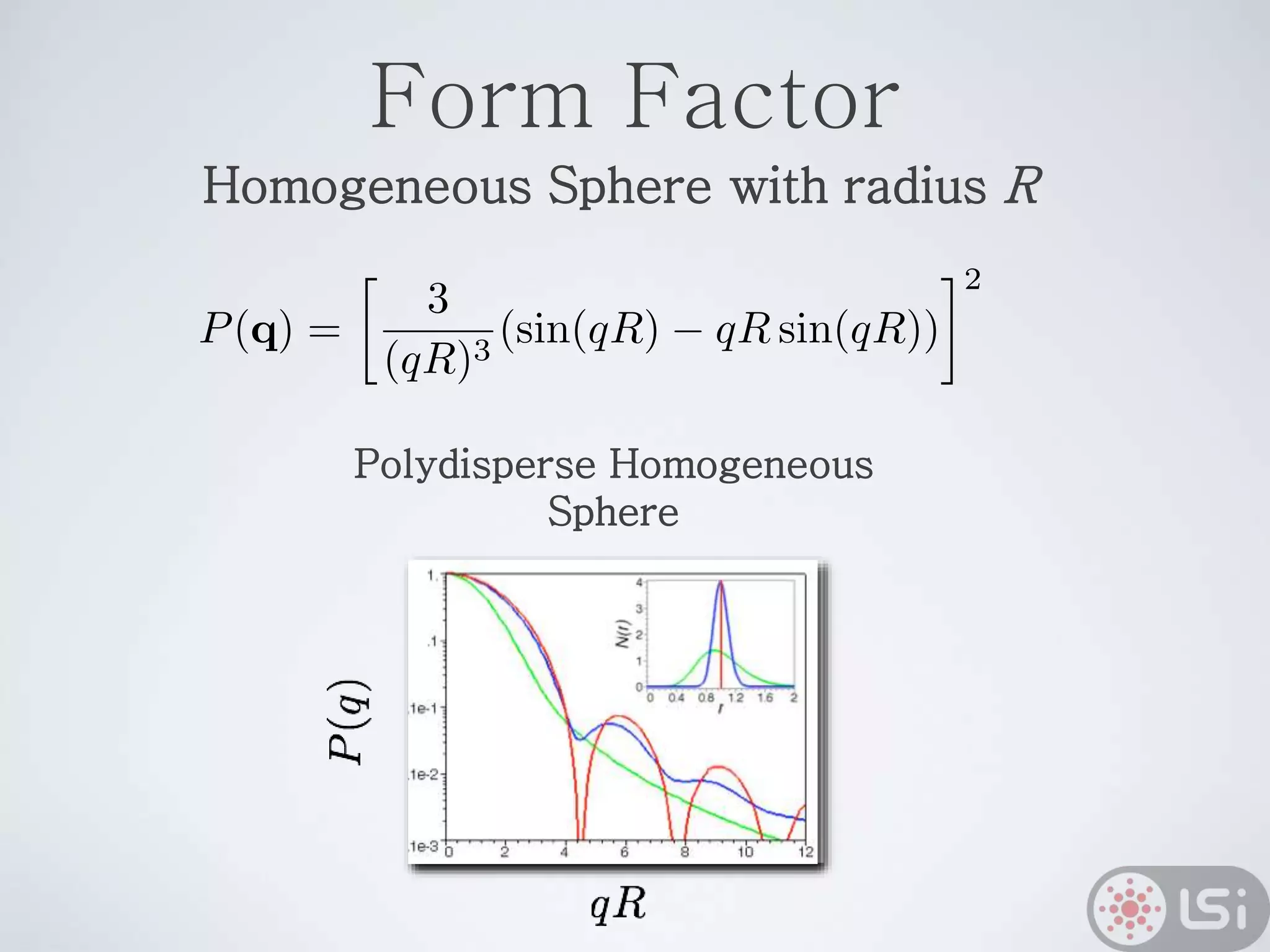
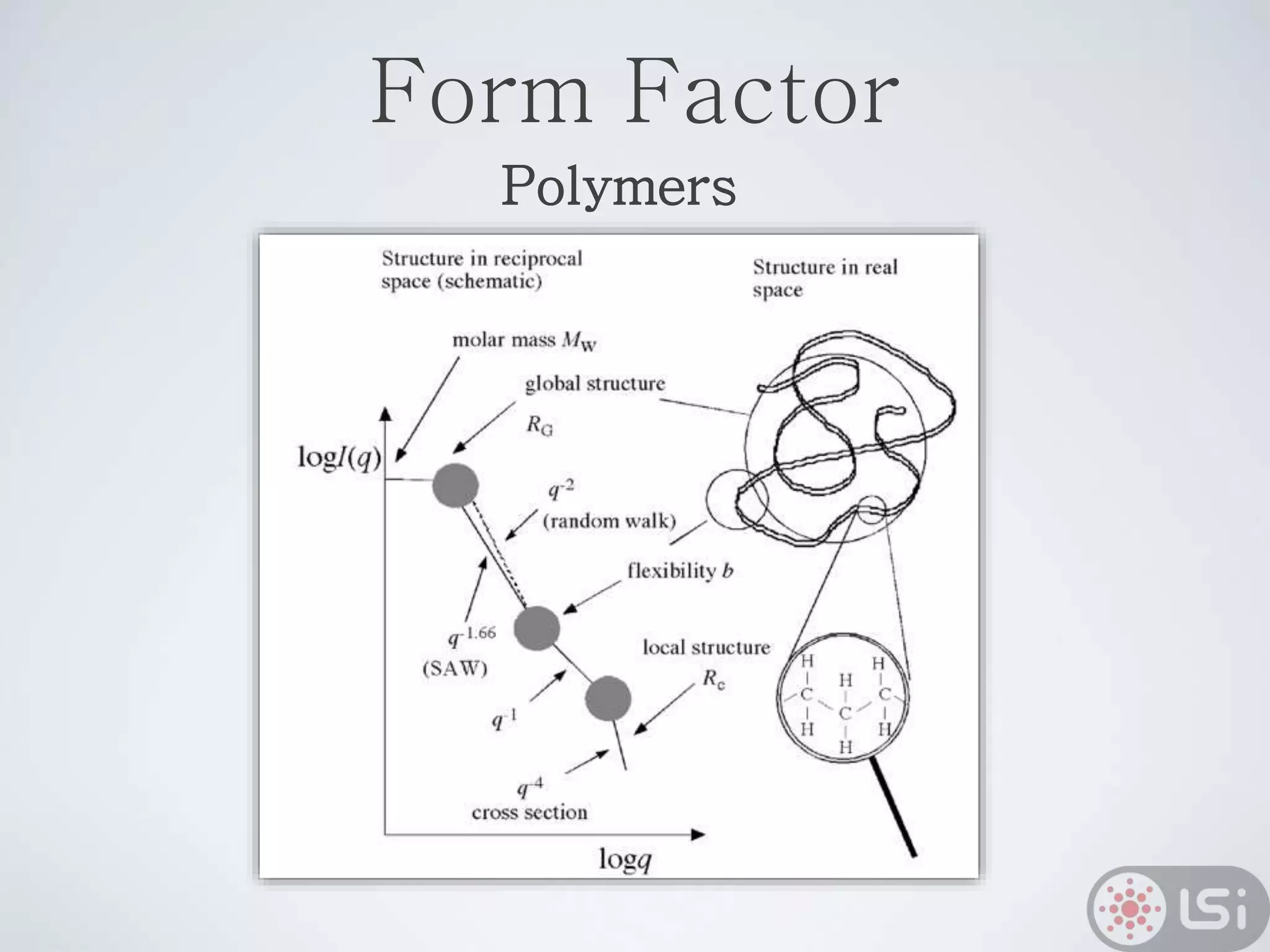
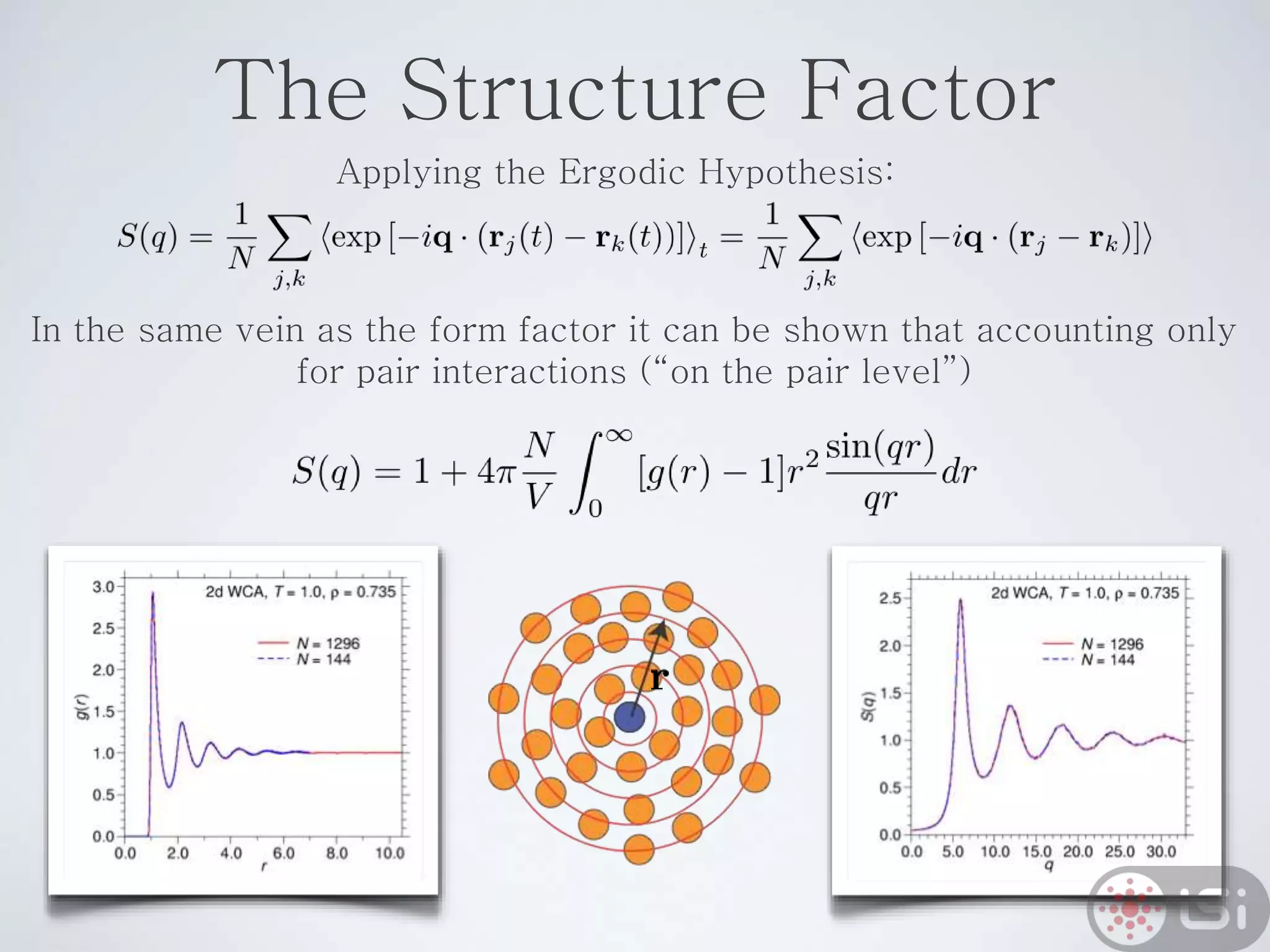
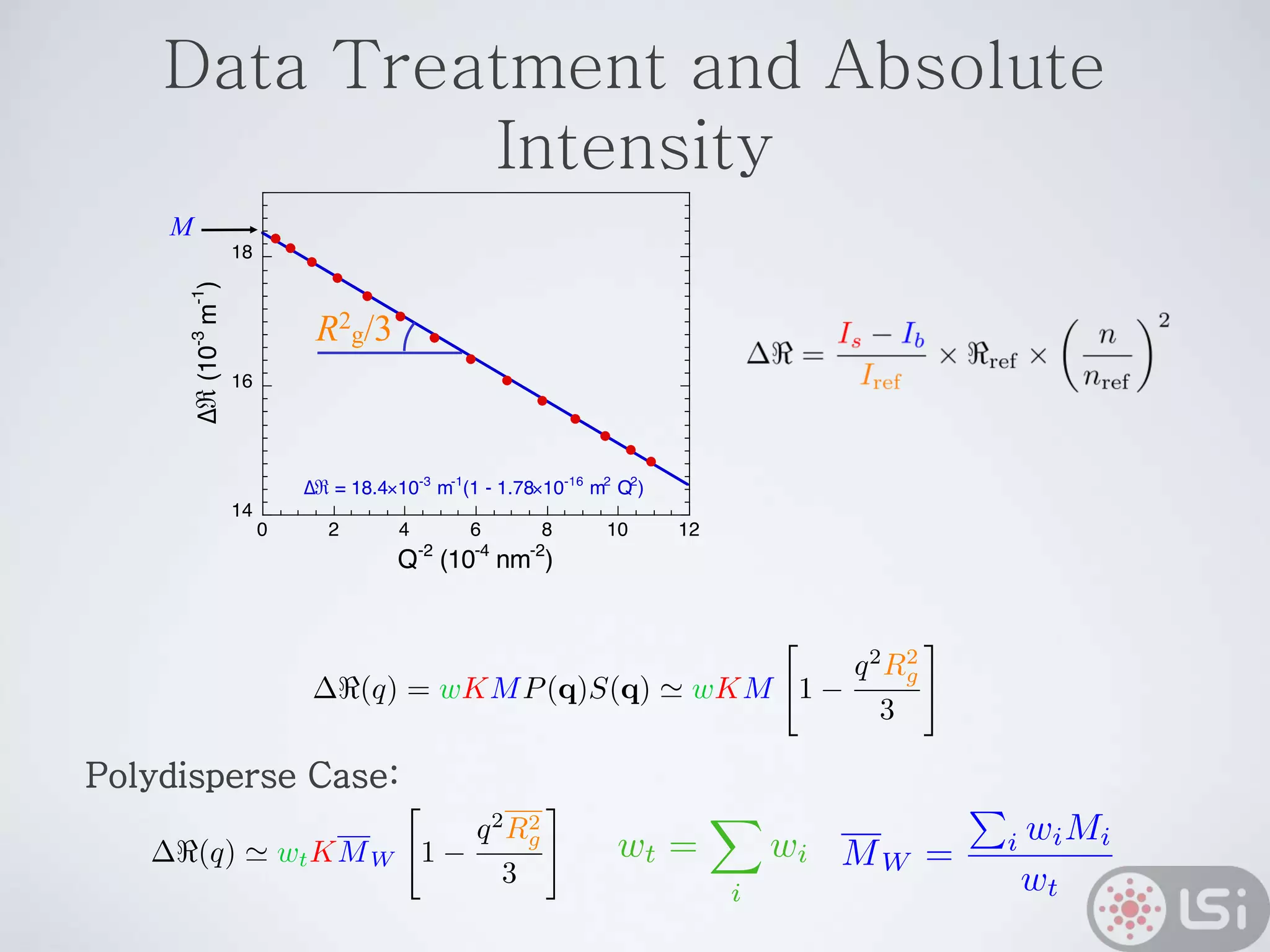
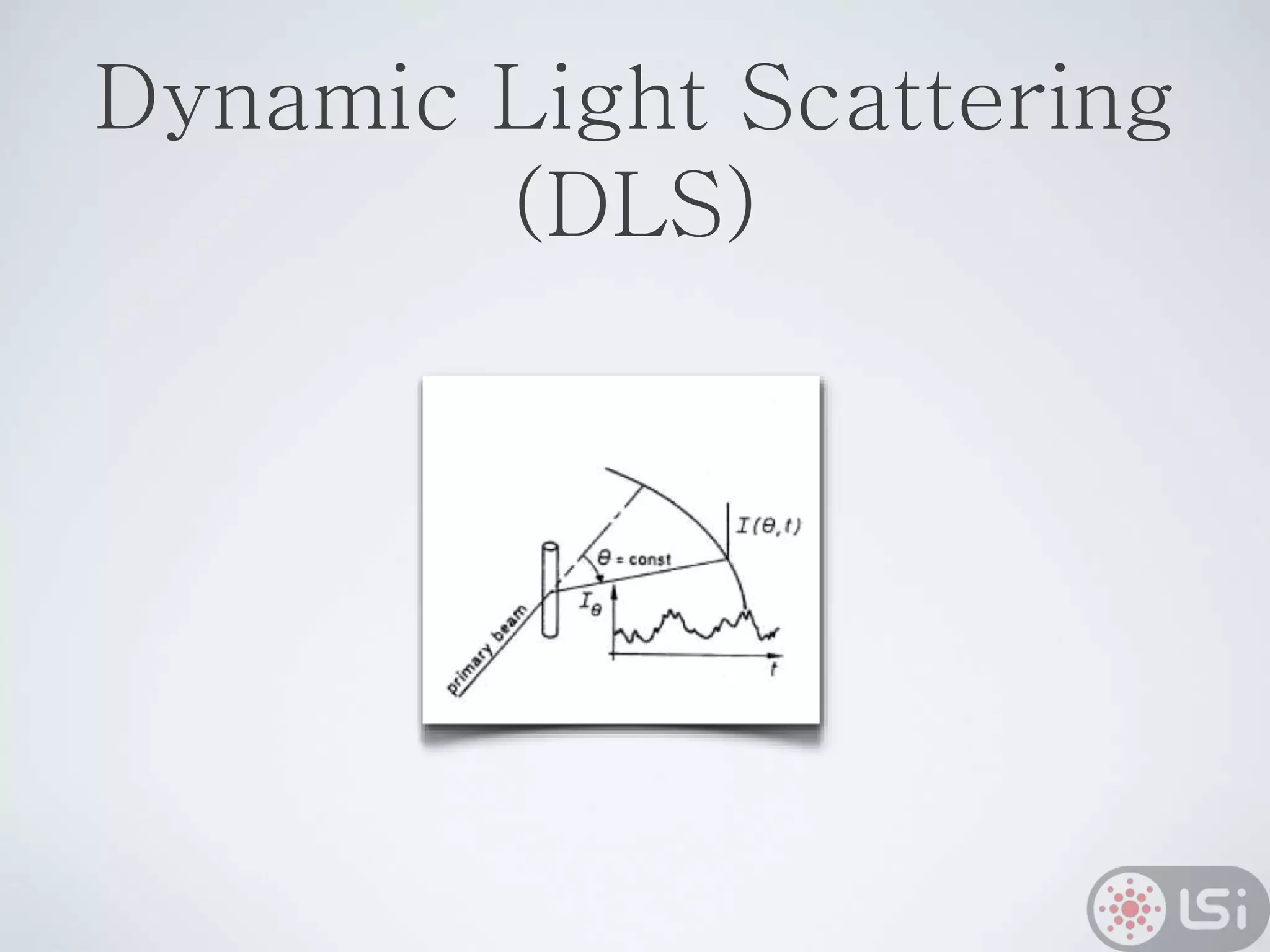
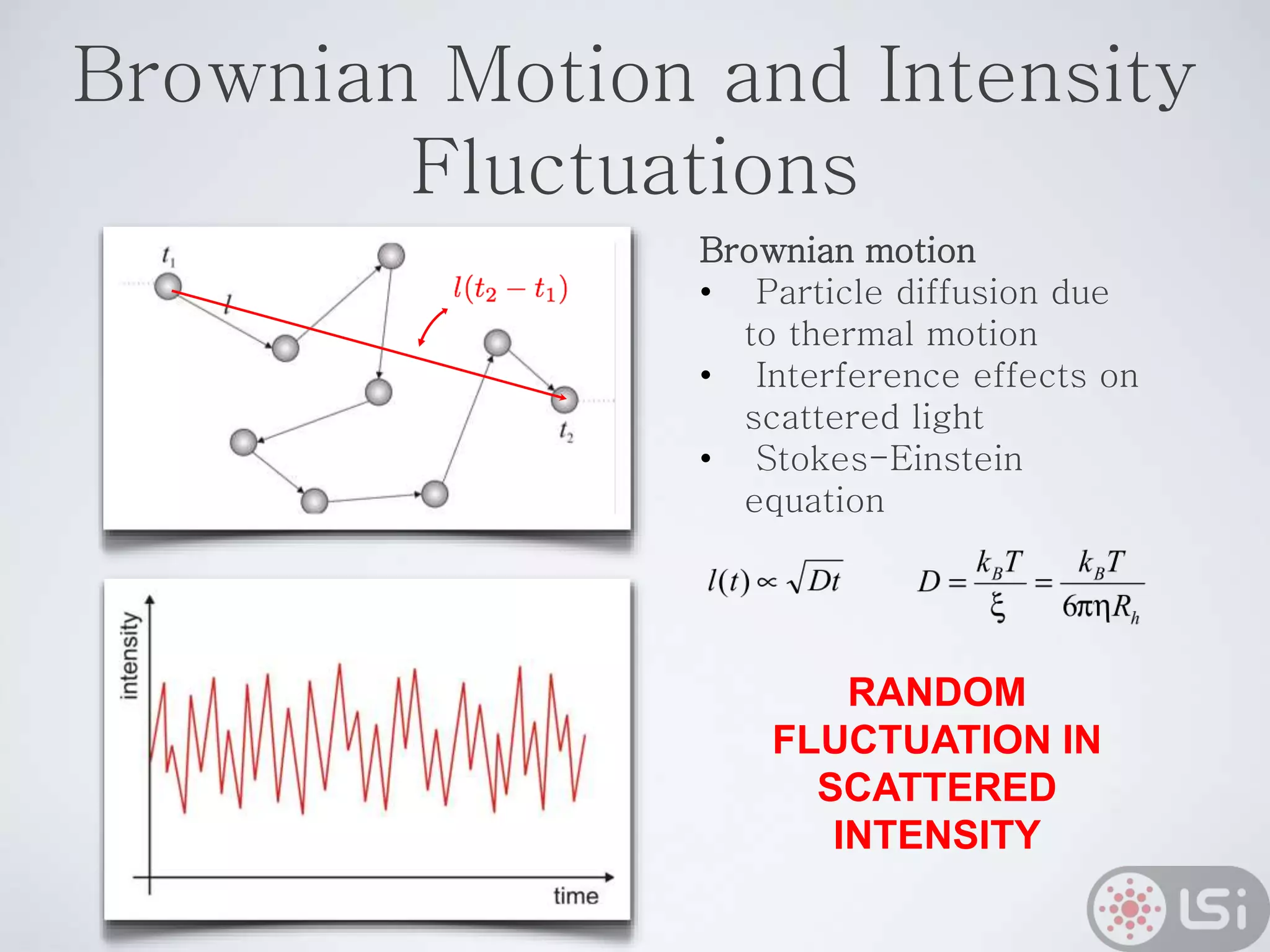
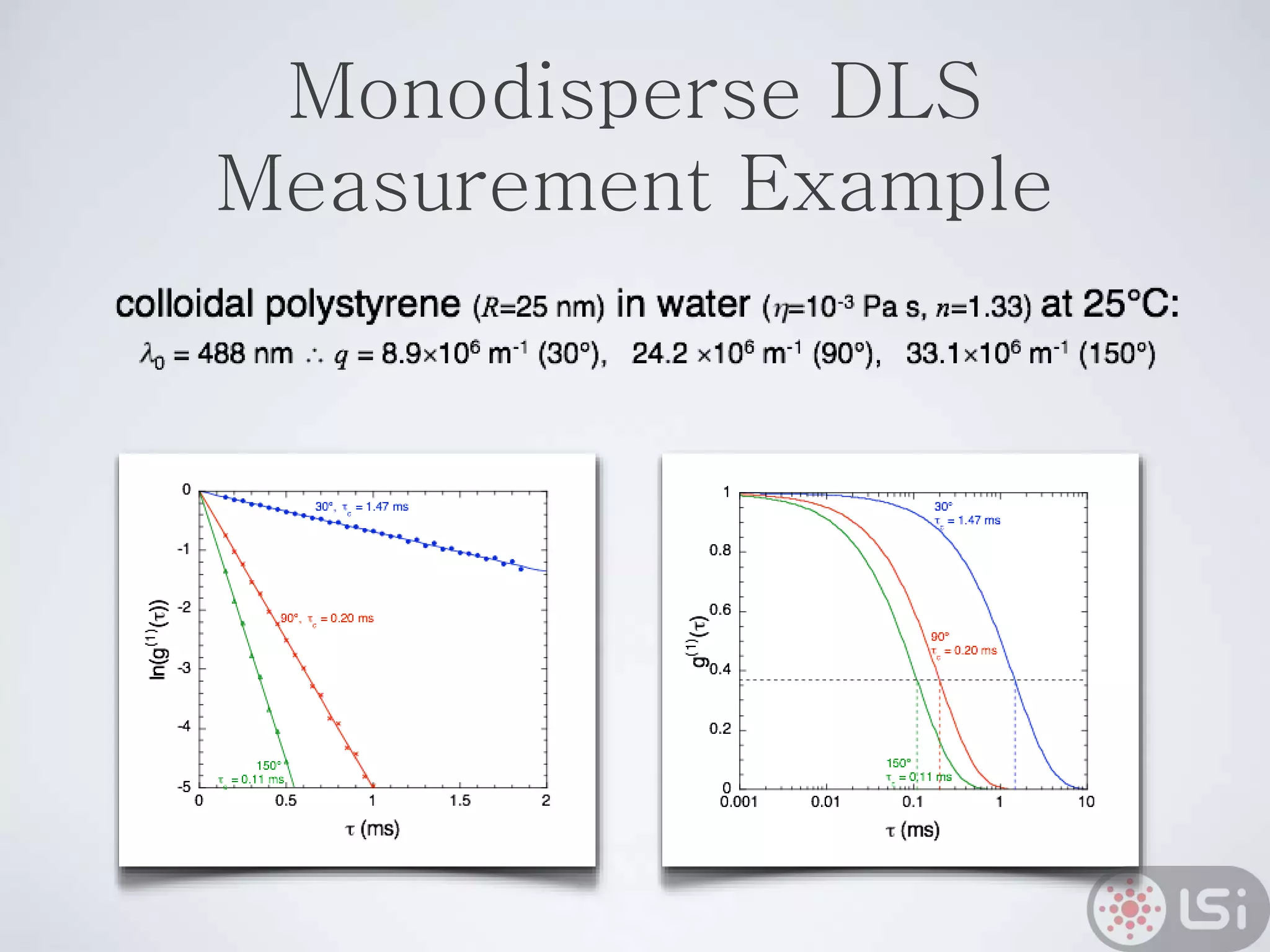
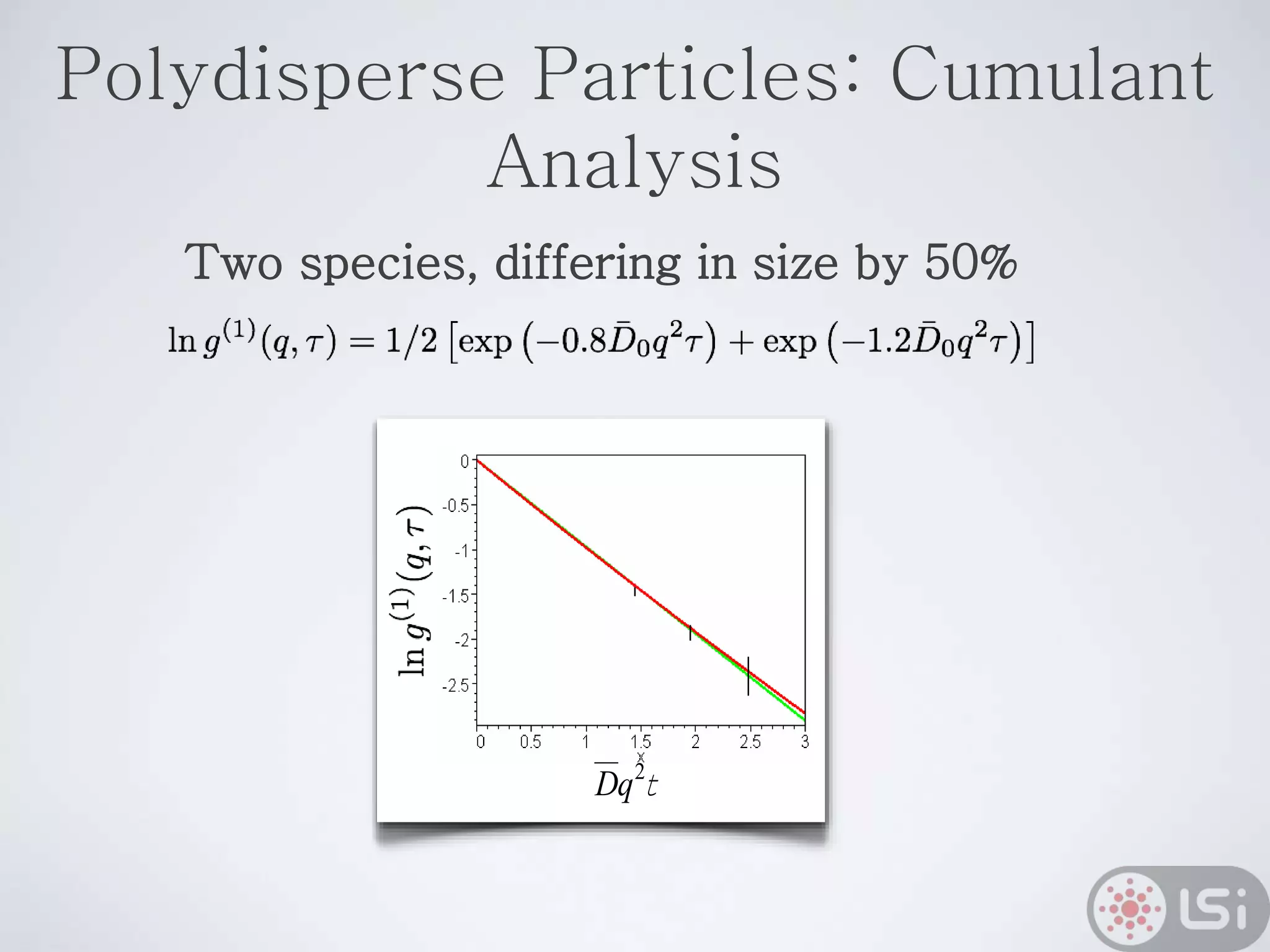
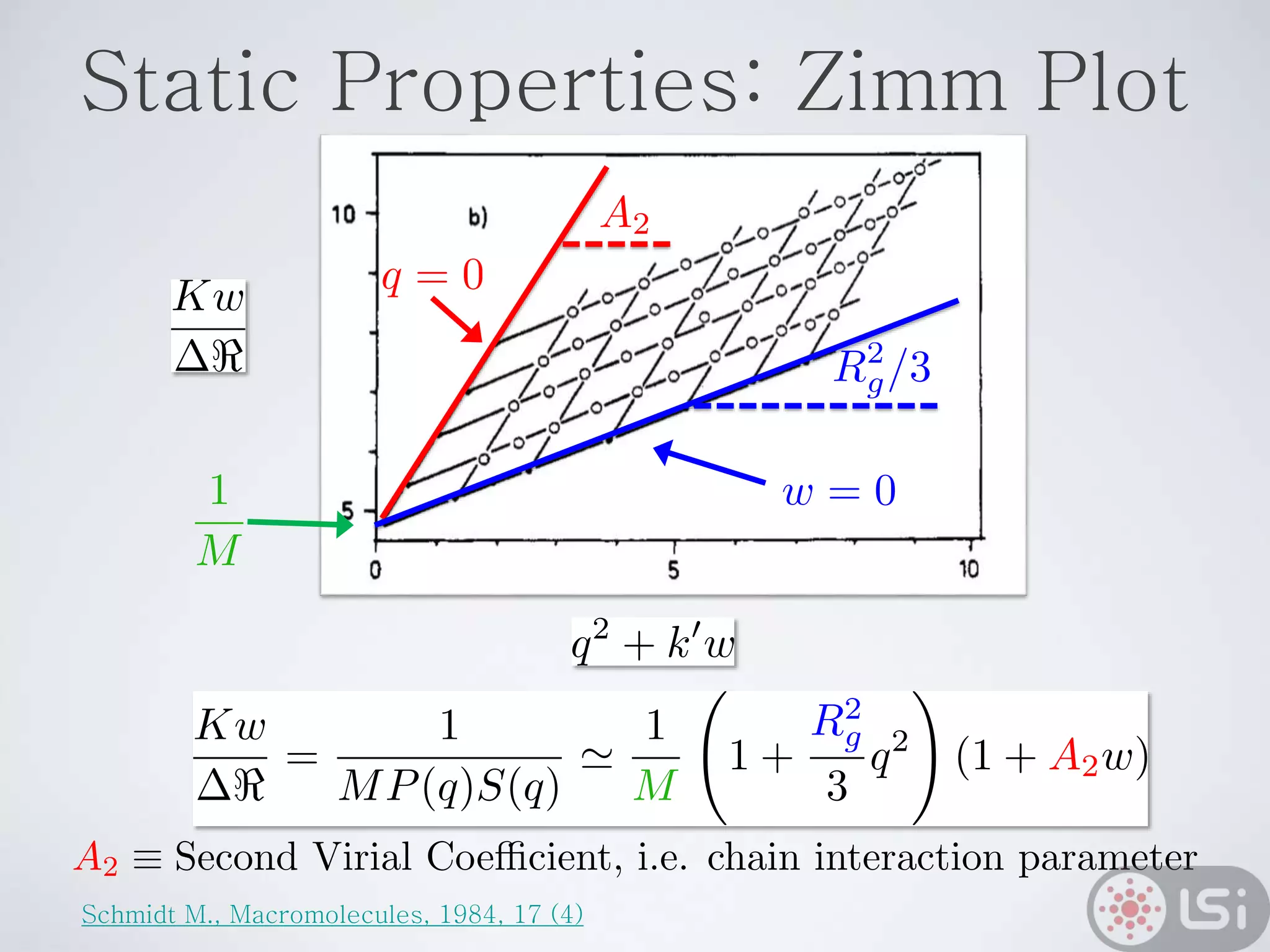
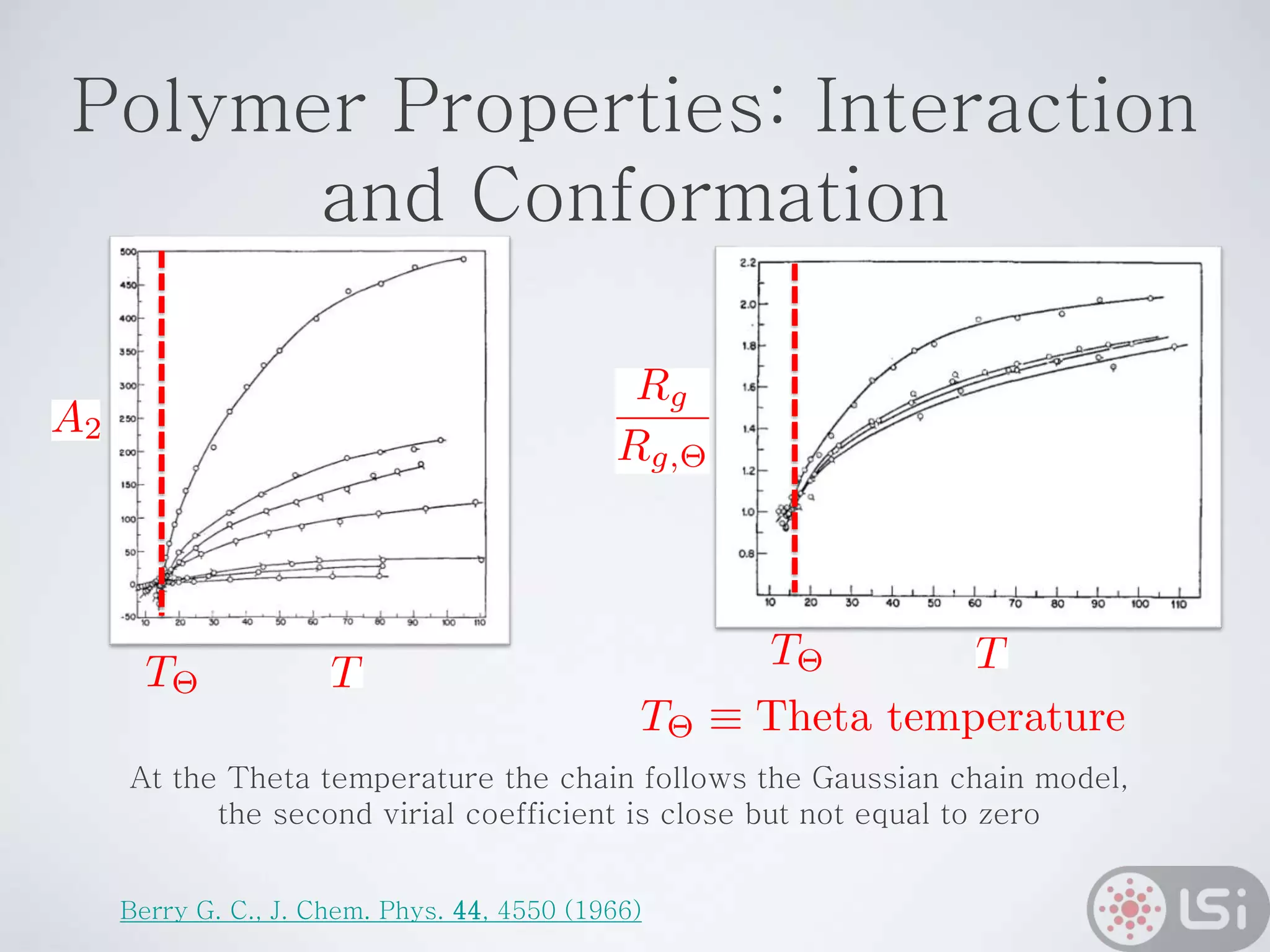
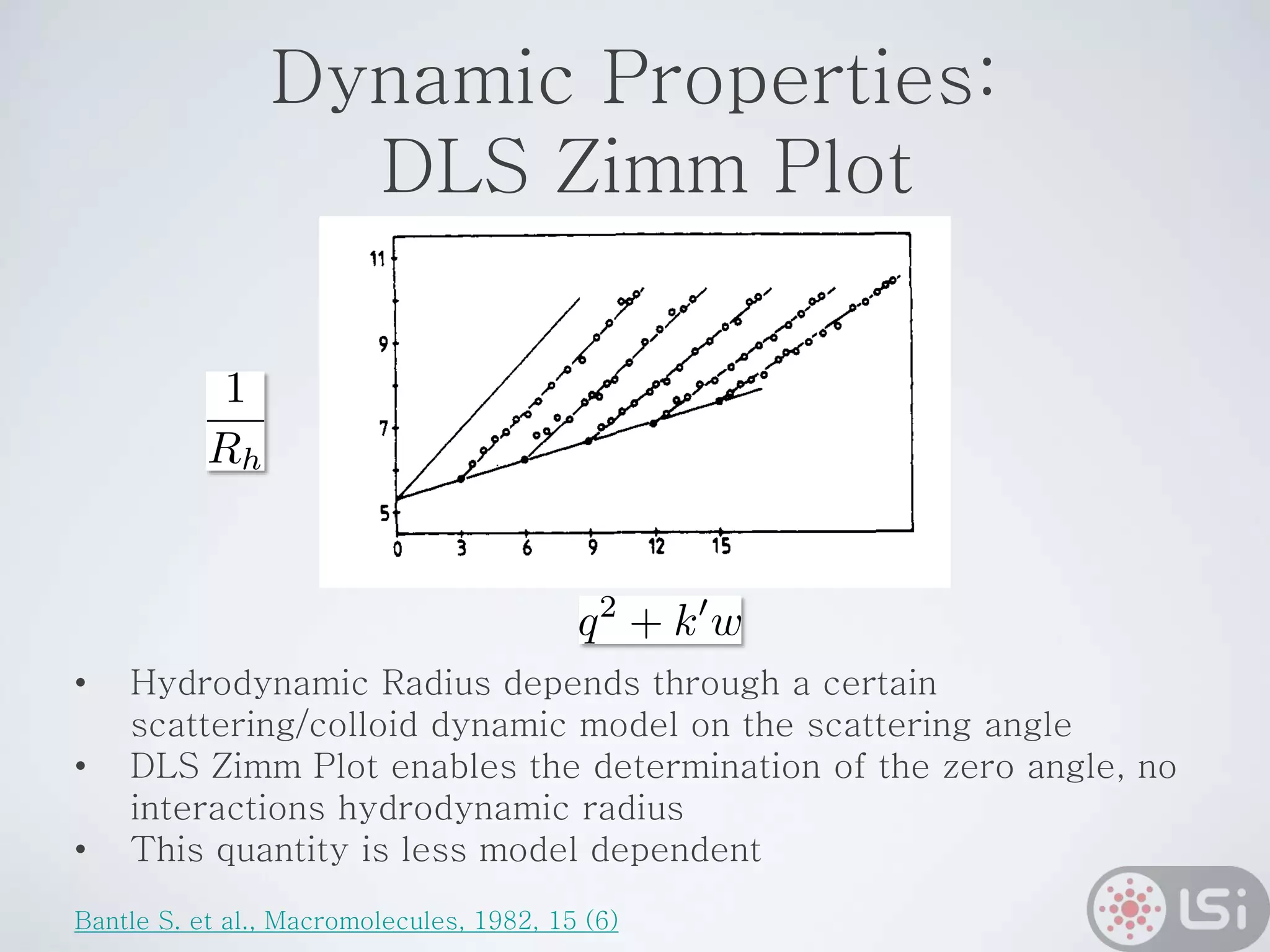
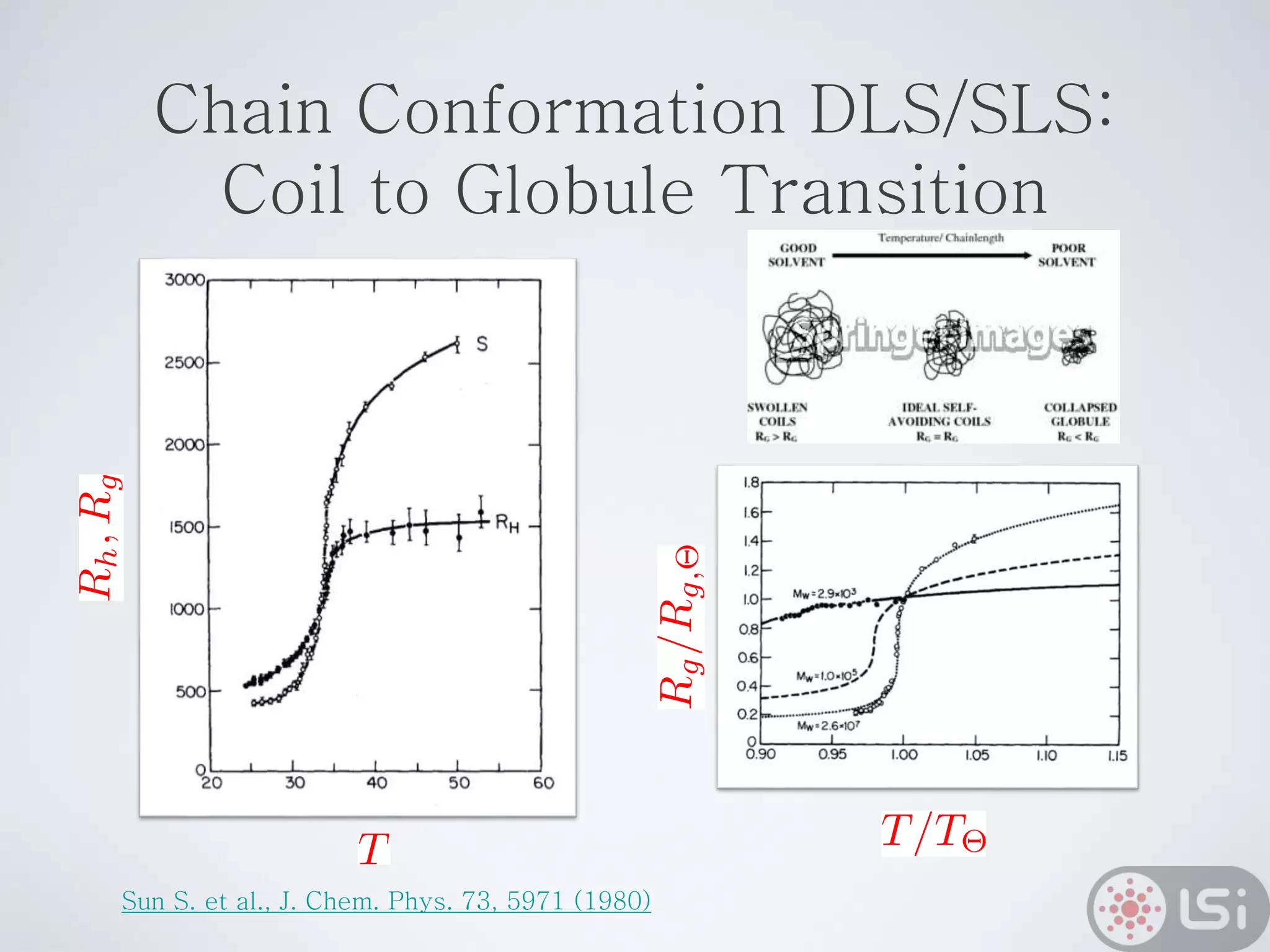
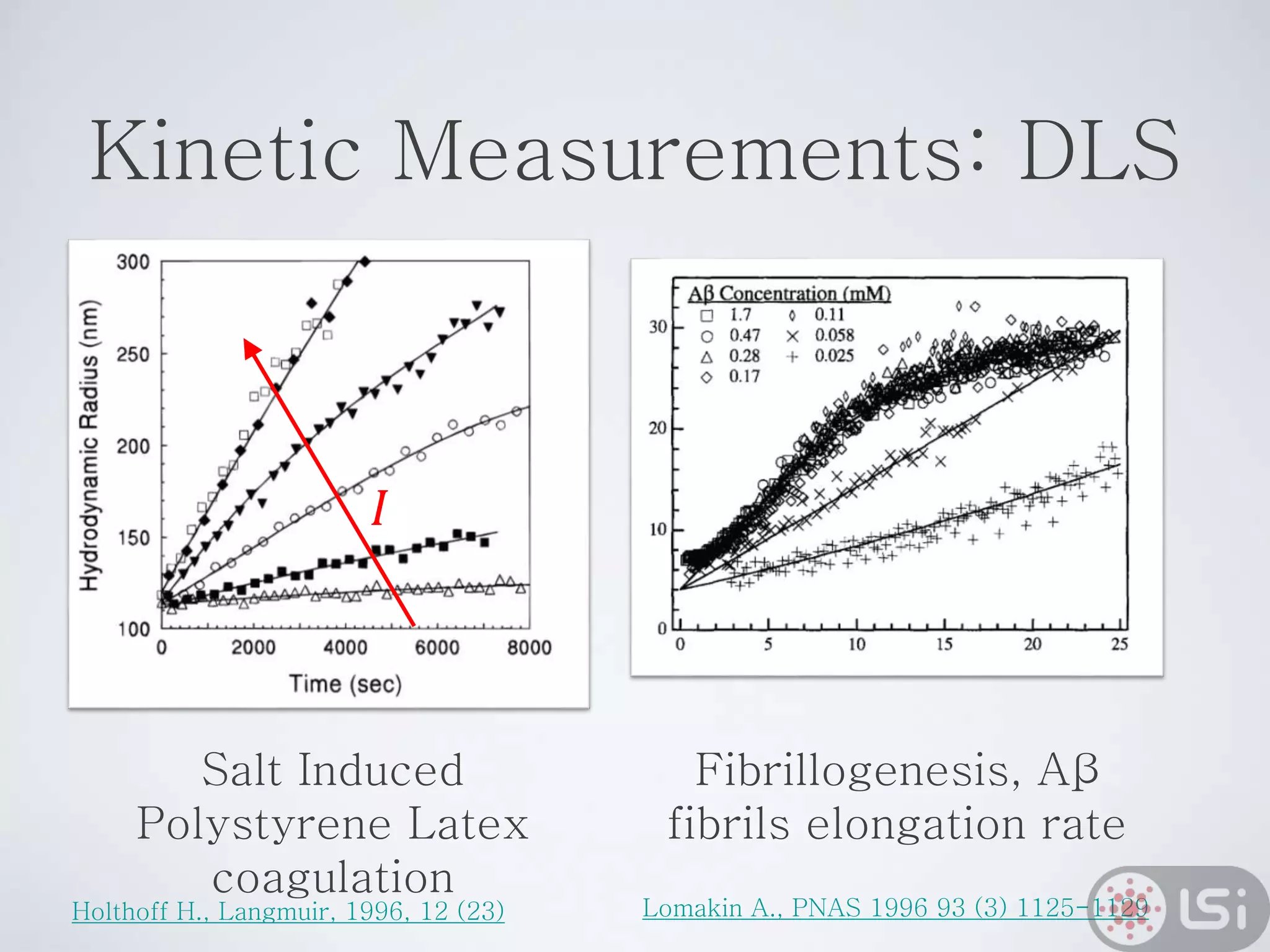
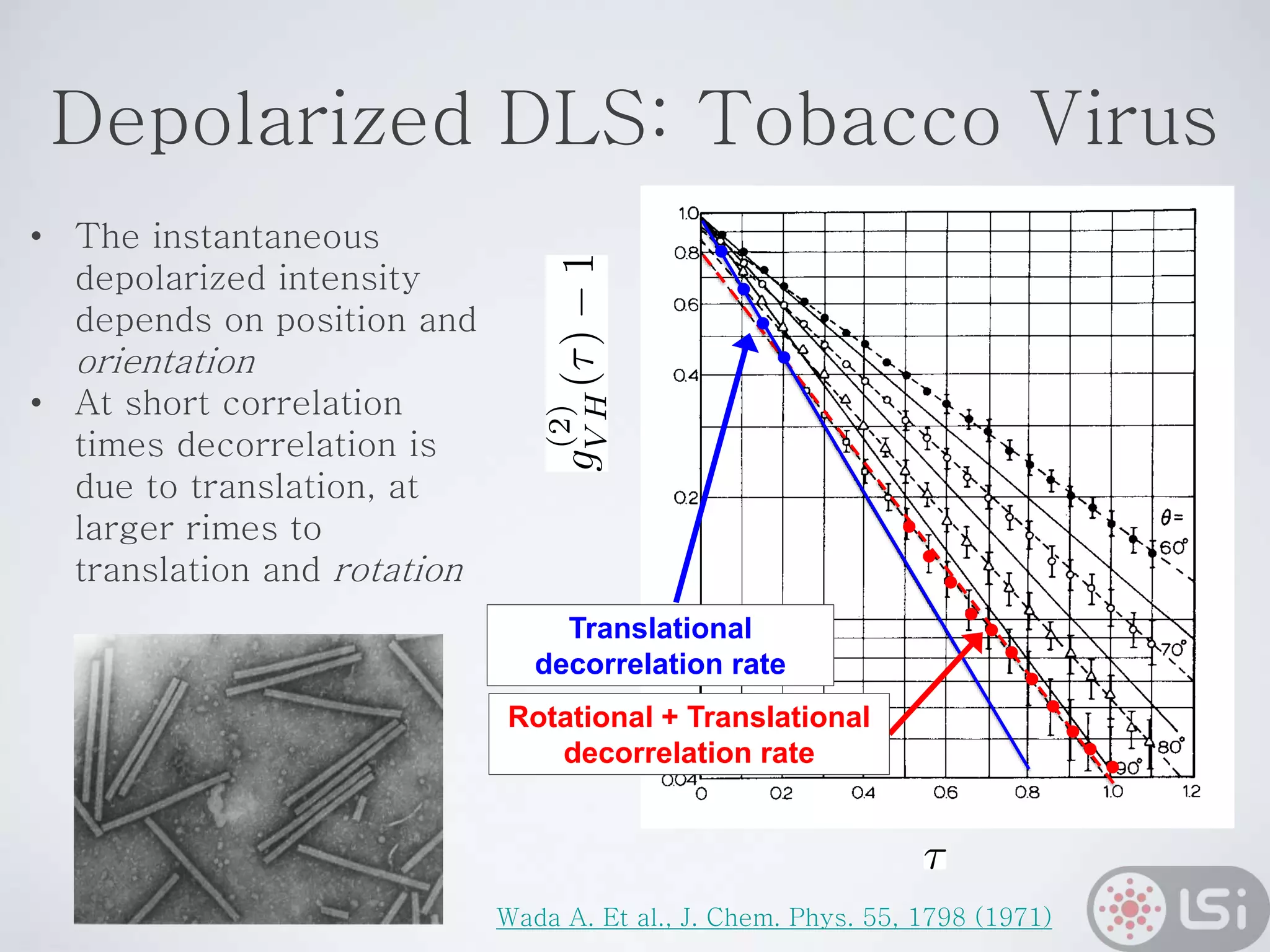
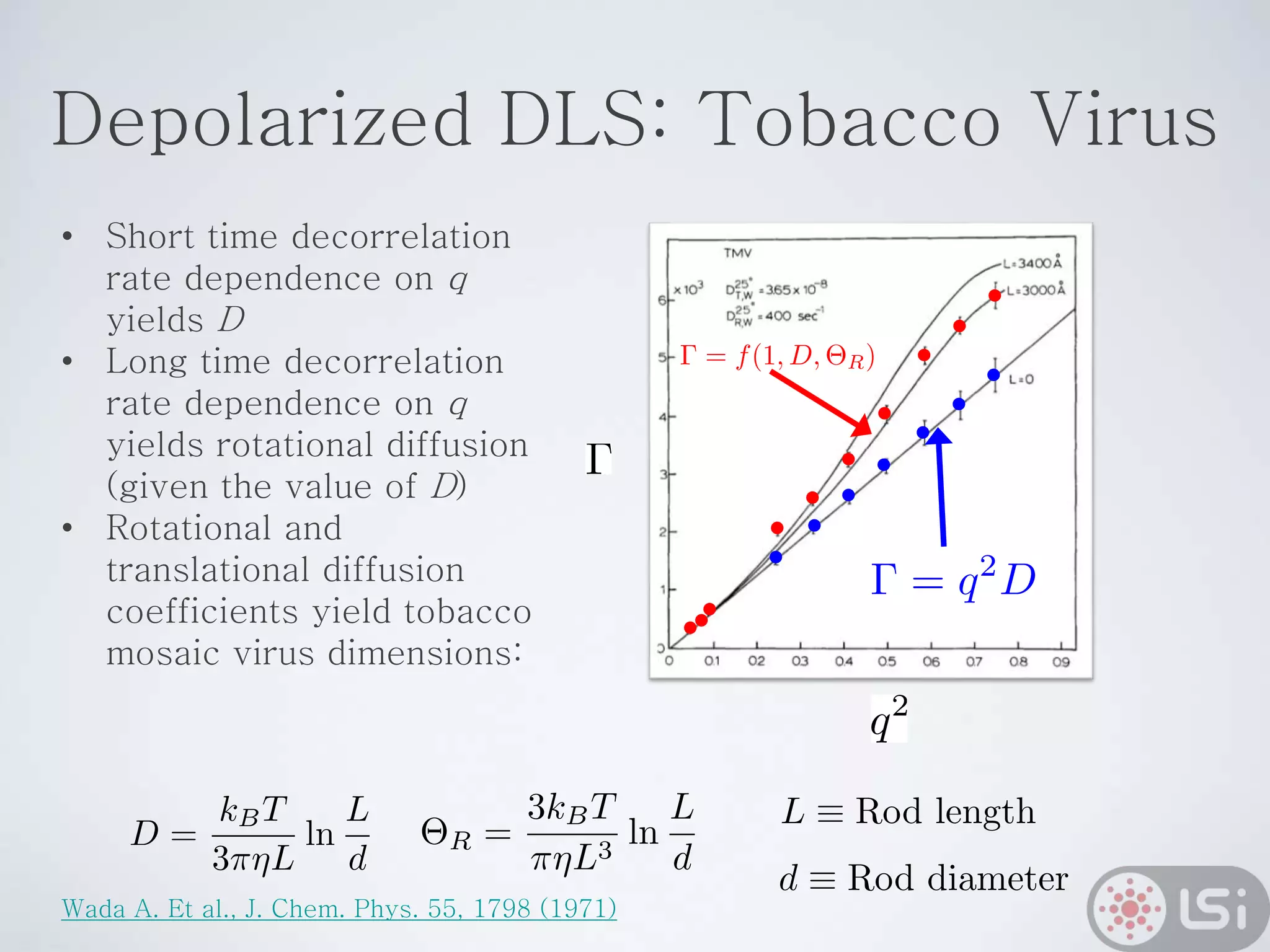
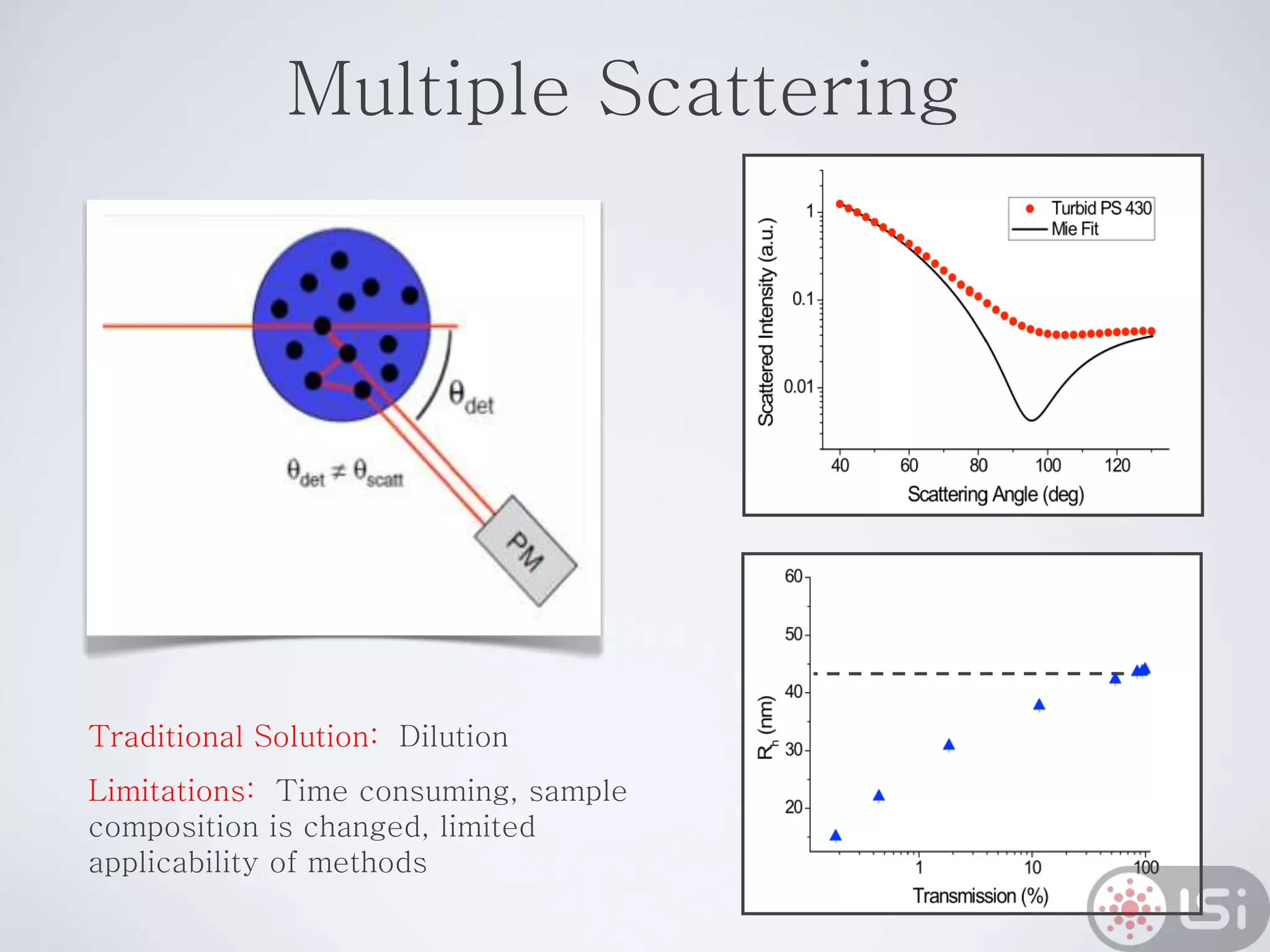
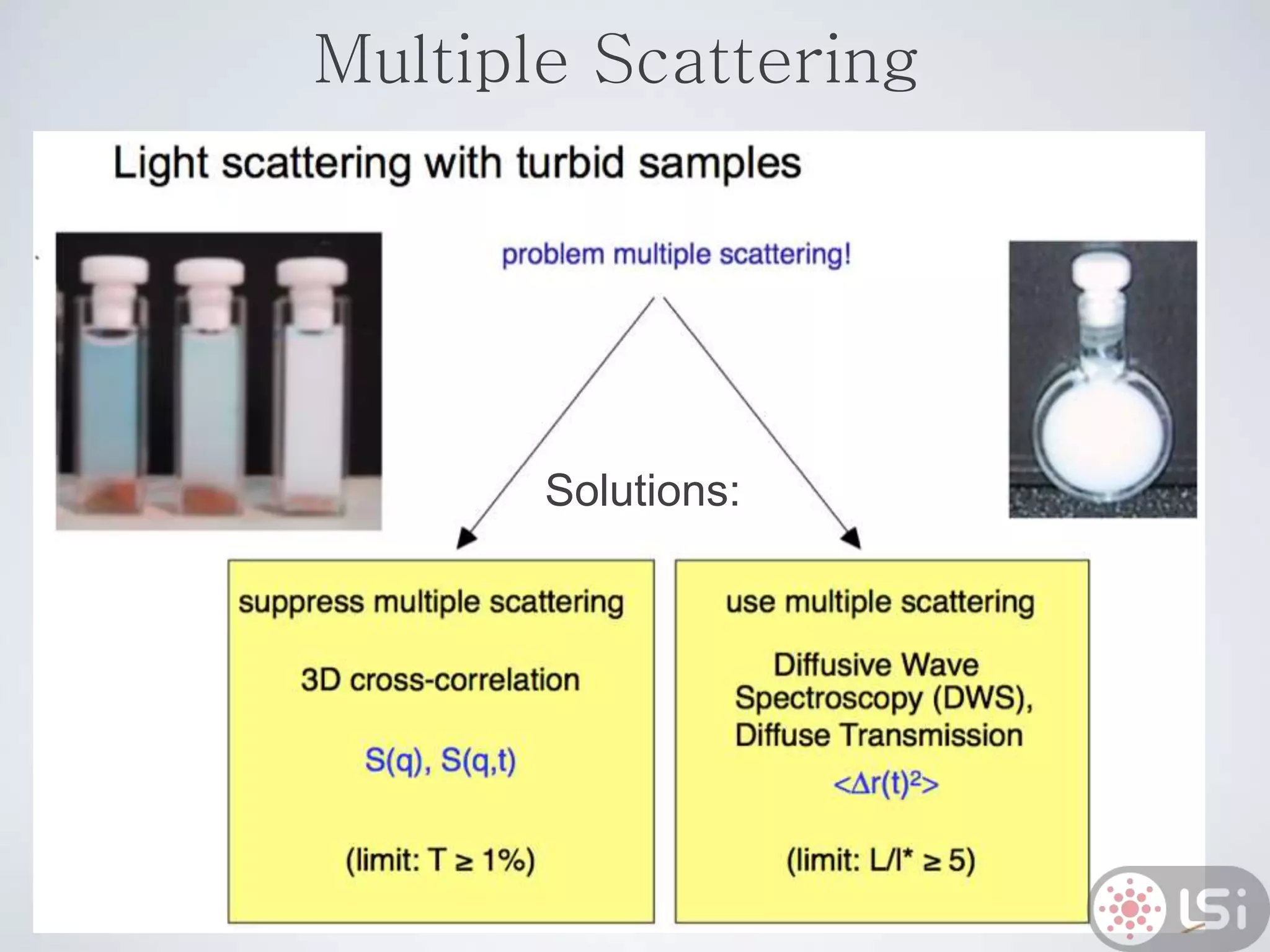
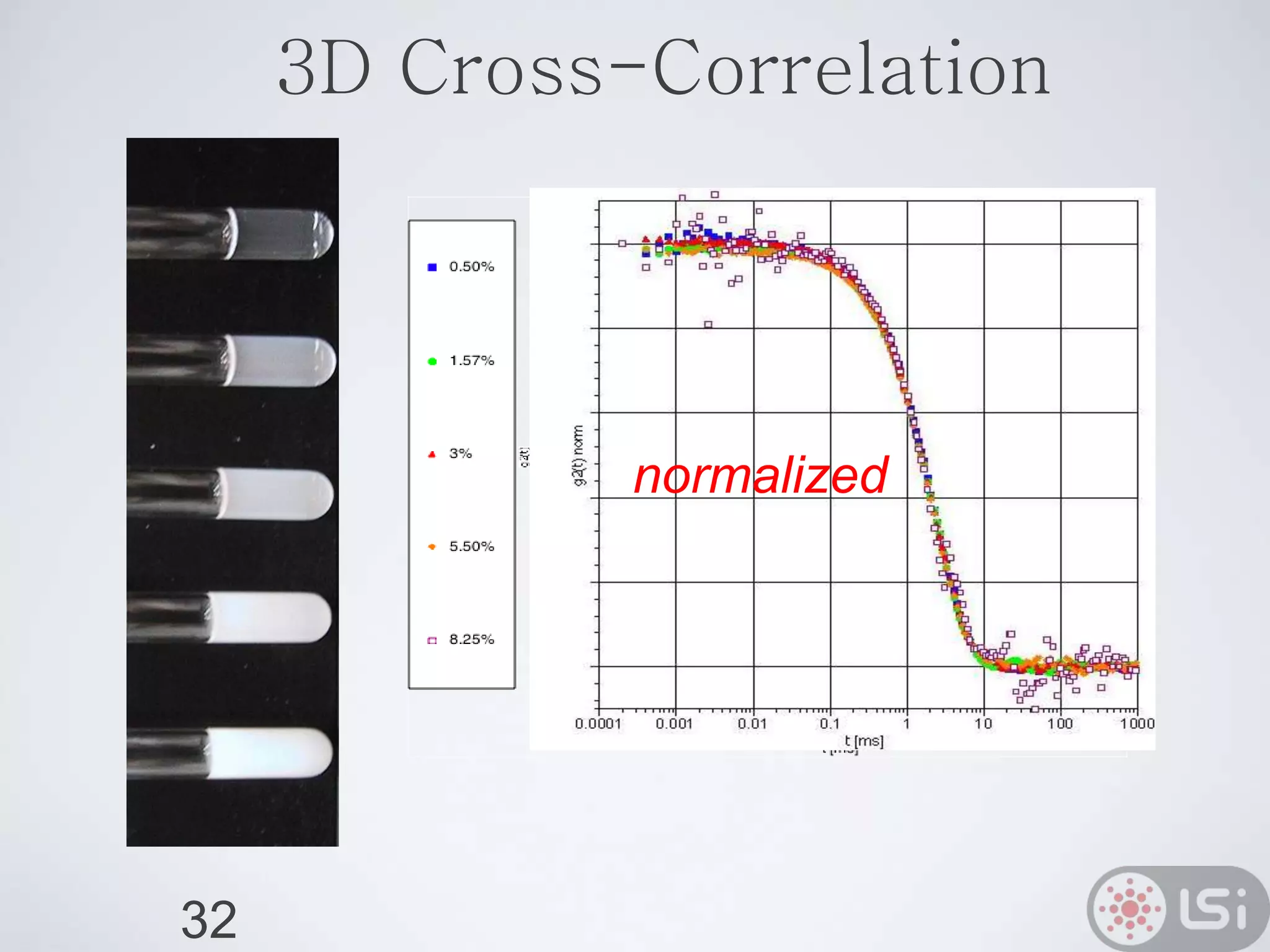
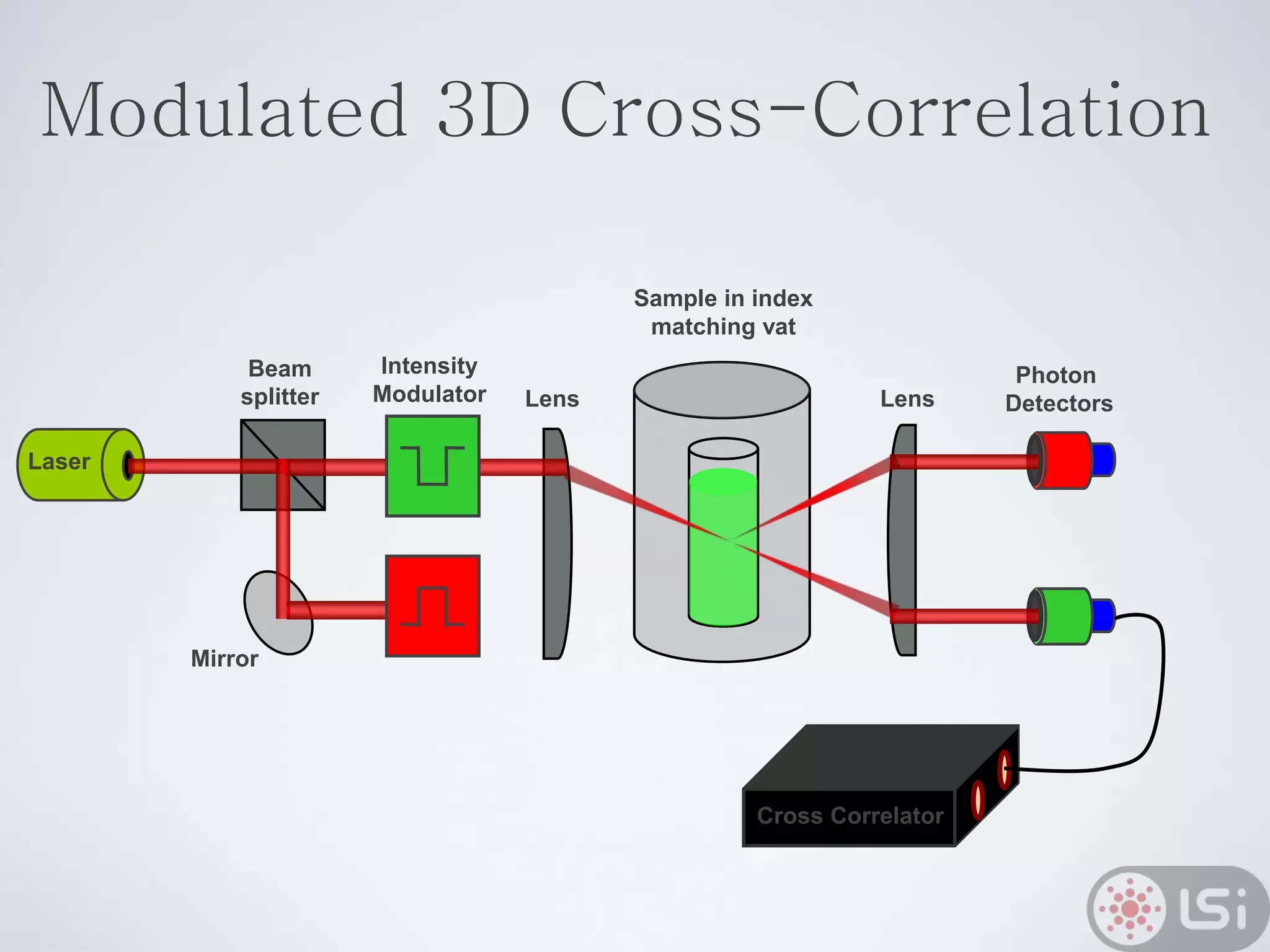
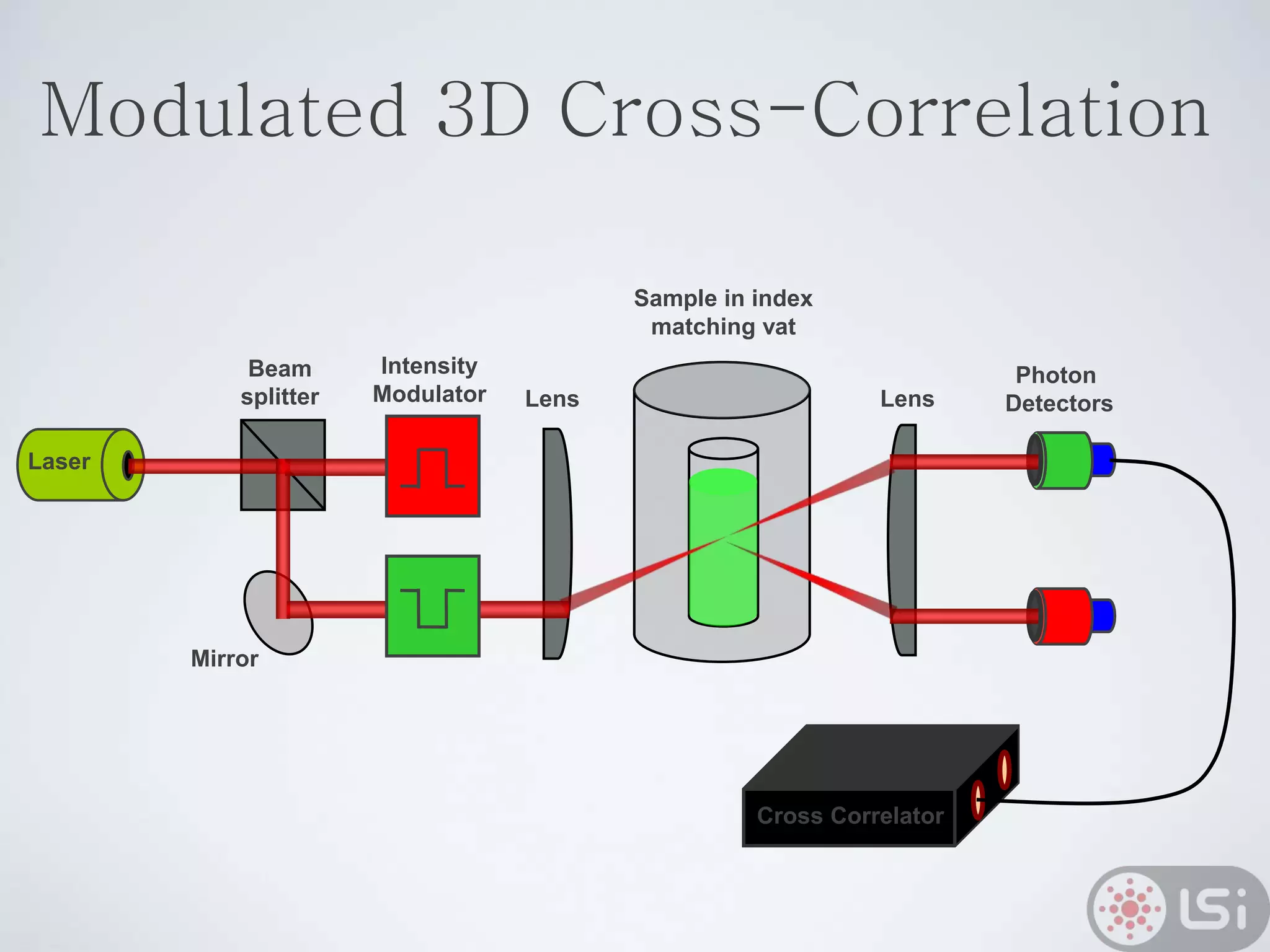
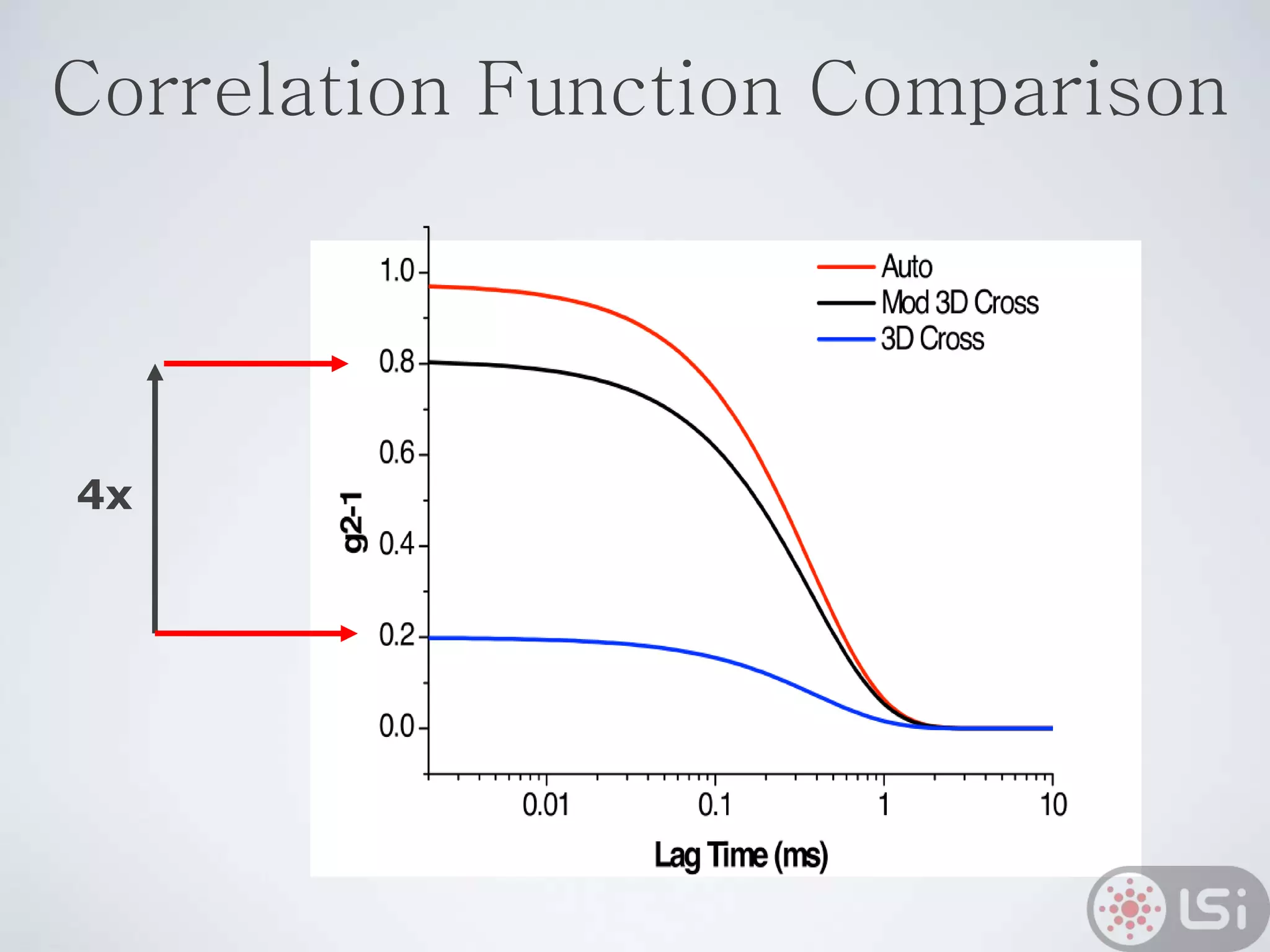
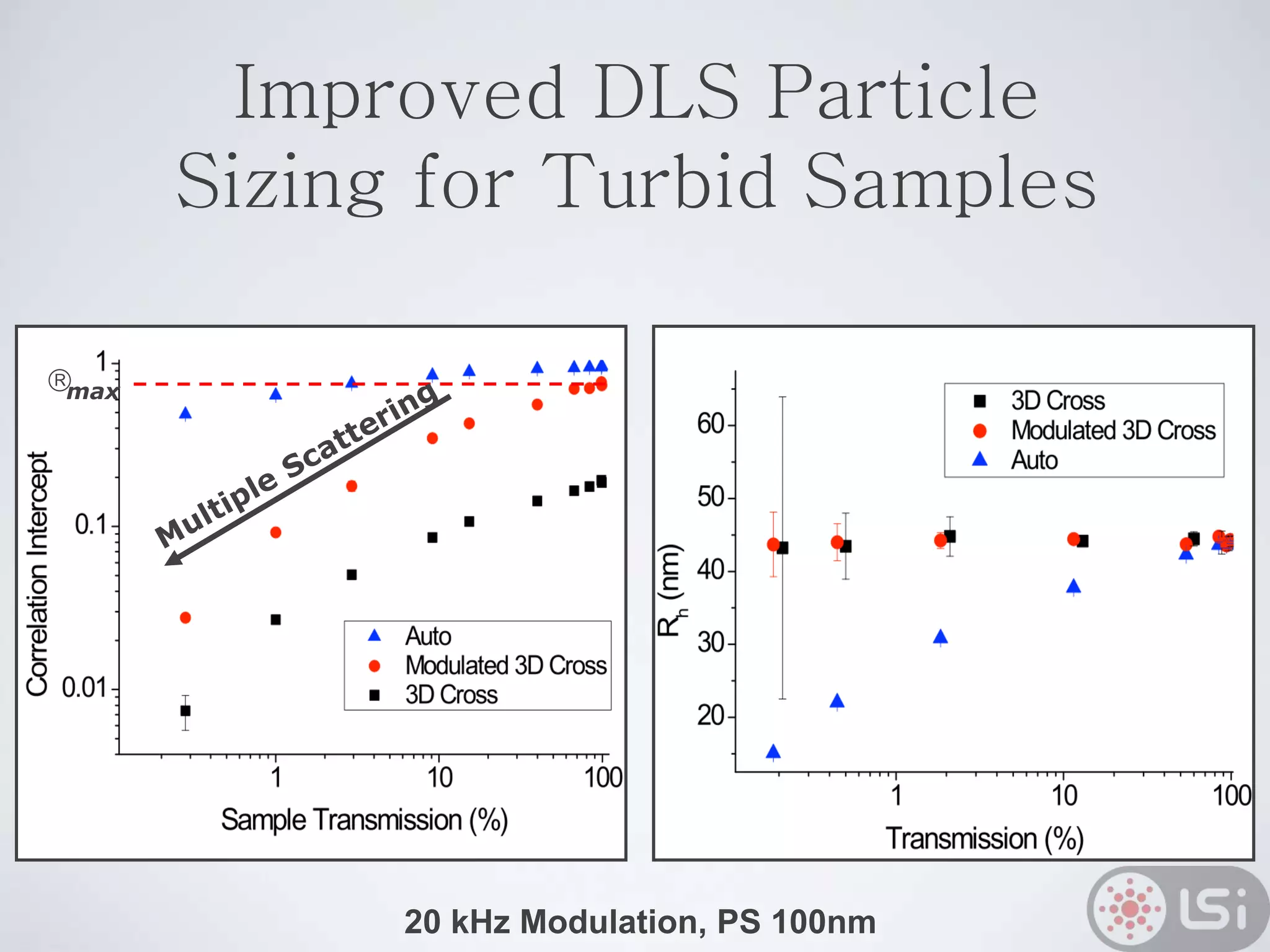
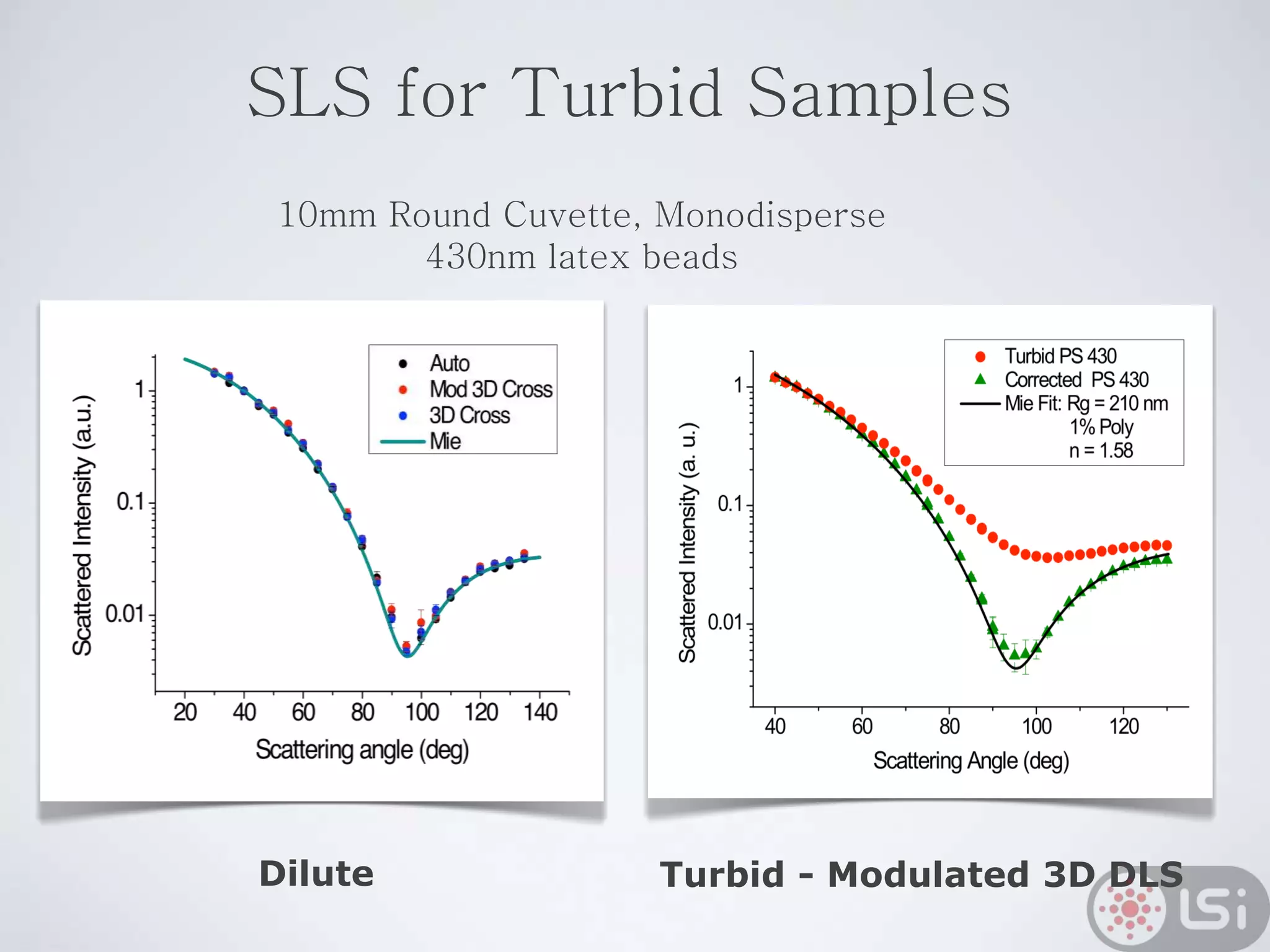
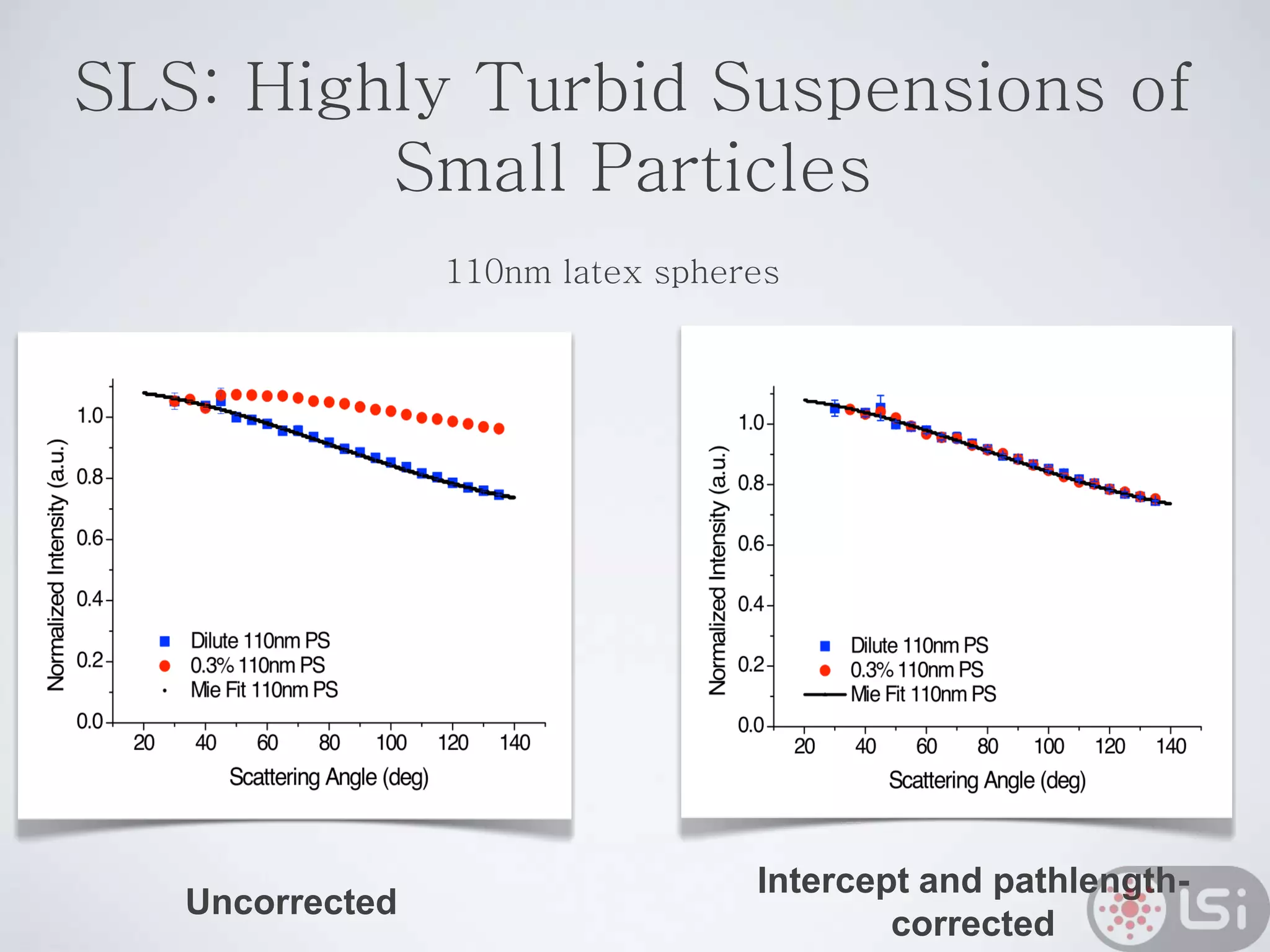
Light scattering can be used as a sizing tool for nanoparticles and macromolecules. There are two main types: static light scattering (SLS) and dynamic light scattering (DLS). SLS measures average scattered intensity which provides information on molecular weight and size. DLS measures intensity fluctuations over time which reveal particle diffusion and hydrodynamic radius. The document outlines theories of light scattering including Rayleigh-Gans-Debye and Mie scattering. It also discusses how to apply light scattering to characterize properties of polymers and other systems, both dilute and highly concentrated.
More Related Content
Similar to Light Scattering Fundamentals (2019 Logo)
Light Scattering Fundamentals (2019 Logo)
- 1. Light Scattering: Fundamentals Andrea Vaccaro,LS Instruments
- 2. “Scattering” of Light particledispersion water
- 3. Light Scattering asSizing Tool Nanoparticles: 1-100 nm Polymers, Macromolecules Clays, Oxides, Proteins etc.
- 4.
- 5.
- 6. Physical Origin ofScattered Light • An electron in the atomic cloud is subject to a force due to the electric field • The cloud deforms and a dipole is induced • As the field oscillates so does the dipole moment • The resulting charge movement radiates (“scatters”) light • “Elastic” scattering: momentum is preserved, no energy loss ⇒ + – Light
- 7. A Collection ofAtoms Field scattered by a dipole of momentum Spherical Wave Scattering Geometry
- 8. A Collection ofAtoms By definition of polarizability For an object smaller than λ (Clausius-Mossotti Relation):
- 9. A Collection ofAtoms Spherical Wave Contrast: Ability to scatter of the material Piecing everything together: Scattering Geometry
- 10. Origin of theScattering Contrast • Interference • For a larger object it is possible to find a second lump that scatters out of phase and with the same amplitude • Completely destructive interference • For an infinite object it is always possible to do this ⇒ No contrast
- 11. The Measured Quantity: theScattered Intensity • Whatever the detection technology, the observable quantity is not the electric field but the flux of energy, the so-called light intensity • It can be shown that in most conditions • In practice the intensity fluctuates in time • In SLS experiment the average intensity is measured
- 12. SLS Theoretical Approaches Theory Assumption Rayleigh(Electrostatic Approximation) Rayleigh-Gans-Debye (RGD, Optically “Soft” Particles) Mie Scattering None Fraunhofer (Geometrical Optics)
- 13. RGD Theory • Assumption:The field inside the particle is the incident field • To satisfy this assumption we must require for the incident field: i) no reflection at the particle/solvent interface ii) no phase change within the particle i) ii) • Every small lump in the particle scatters as if it were “alone”
- 14. RGD Interference: TheScattering Vector Interference Term Dropping the dummy time dependency terms:
- 15. The Meaning ofthe Scattering Vector The module of the scattering vector has dimensions of inverse of length: q-1 is the length-scale of the interference phenomenon. Two material lumps farther than q-1 interfere destructively. Closer than q-1 interfere additively Destructive Interference, Smaller Intensities No internal Interference Maximum Intensity q-1 can be interpreted as a rough measure of the probed length-scale
- 16. One Particle: TheScattering Amplitude Integrating previous equation over the whole particle: Labeling the particle with the subscript j and factoring out its position by means the variable substitution We obtain Particle j scattering amplitude Interference : Particle Position Internal Interference
- 17. An Ensemble ofParticles Previous result allows to sum each contribution = 0 = 0 ! Independent position and orientation We measure a time average:
- 18. RGD Scattered Intensity Indeedthe electric field in not an observable But intensity is: Average Contrast Structure Factor: Interparticle Interference Form Factor: Intraparticle Interference Scattering Geometry • The RGD assumption results in the factorization of different contributions • Same factorization for polydisperse systems After many manipulations:
- 19. The Ergodic Hypothesis Oneof the starting hypotheses od statistical mechanics is the so called “Ergodic Hypothesis”: For any system at equilibrium infinite time averages of observable quantities are equivalent to ensemble averages, i.e.: An ensamble average, is an average over the ensable of all the feasible physical configurations. Once we know how to construct such an ensemble this hypothesis enables us to “calculate” observed time averaged quantities
- 20. Form Factor Homogeneous Spherewith radius R Polydisperse Homogeneous Sphere
- 21. Form Factor Non radiallysymmetric shapes Scattering length density weighted pair distance function:
- 22. Form Factor atSmall q: The Radius of Gyration Expanding in series the interference factor... The form factor becomes Radius of Gyration: In a plot of the intensity vs. q2 the extrapolation to zero yields a size parameter that is model independent
- 23. Radius of Gyration:Polydisperse Case
- 24.
- 25. The Structure Factor Inthe same vein as the form factor it can be shown that accounting only for pair interactions (“on the pair level”) Applying the Ergodic Hypothesis:
- 26. The Rayleigh Ratio Scattered Intensity TheRayleigh Ratio: Scattered intensity per unit incident intensity, unit solid angle, and unit scattering volume. Depends only on the thermodynamic state of the solvent not on the measuring apparatus Mass Concentration Sample Contrast Molar MassInstrumental Constant Solvent Scattering (Background)
- 27. Absolute Measurements • Knowledgeof the constant A enables absolute intensity measurements • Absolute measurements allow for the determination of the radius of gyration and the second virial coefficient but also of the molar mass M, or the particle concentration • How do we do it? Excess Rayleigh Ratio:
- 28. Absolute Measurements: How •Scientists have built special devices that allow the measurement of Rayleigh ratios, values for common reference solvents are available in literature • If we measure the same reference solvent in the same thermodynamic conditions we have: Substituting back:
- 29. Data Treatment andAbsolute Intensity M R2 g/3 Polydisperse Case:
- 30. Macromolecular Systems • Thetreatment so far was focused on particulate systems • For macromolecular systems we cannot precisely define a refractive index, how do we obtain the contrast? Tabulated or Measured Assuming a refractive index mixing rule and in dilute conditions: RGD Hypothesis: m close to 1
- 31.
- 32.
- 33. Particle Dynamics inReal and Reciprocal Space Particle tracking with a microscope Dynamics in reciprocal (Fourier) space
- 34. Brownian Motion andIntensity Fluctuations Brownian motion • Particle diffusion due to thermal motion • Interference effects on scattered light • Stokes-Einstein equation RANDOM FLUCTUATION IN SCATTERED INTENSITY
- 35. Intensity Decorrelation 9 Intensity correlationfunction ∗ small large CORRELATION DECORRELATION >
- 36. Field Correlation Function Uponnormalization: Identical Independent Particles But cannot be measured! The electric field correlation function is important as it is directly connected to colloid dynamics models
- 37. Intensity Correlation Function Assumingthe field be a Gaussian stochastic variable: As for SLS we can measure the intensity correlation function Omitting the scattering amplitudes Fj :
- 38. Coherence Area, Siegert Relationship •In practical implementations the field is not always a Gaussian stochastic variable • This happens since we sometimes image more than one coherence area (“speckle”) • The signal to noise ratio is lowered
- 39. DLS data treatment Identicalparticles (Monodisperse): Brownian diffusion theory
- 40.
- 41. Polydisperse Particles: Cumulant Analysis Intensityweighted correlation function Cumulant Expansion: Typical uncertainty in cv is ± 0.02, i.e. it is hard to determine cv ≤ 0.2 (20%) For a polydisperse sample Intensity weighted diffusion coefficient
- 42. Polydisperse Particles: Cumulant Analysis t2 qD Twospecies, differing in size by 50%
- 43.
- 44. Static Properties: ZimmPlot Schmidt M., Macromolecules, 1984, 17 (4)
- 45. Polymer Properties: Interaction andConformation At the Theta temperature the chain follows the Gaussian chain model, the second virial coefficient is close but not equal to zero Berry G. C., J. Chem. Phys. 44, 4550 (1966)
- 46. Polymer Properties: Chain Conformation Dependencyof chain size on solvent “goodness” Dependency of chain size on molar mass (at Theta solvent conditions) Outer P. et al., J. Chem. Phys. 18, 830 (1950)
- 47. Dynamic Properties: DLS ZimmPlot • Hydrodynamic Radius depends through a certain scattering/colloid dynamic model on the scattering angle • DLS Zimm Plot enables the determination of the zero angle, no interactions hydrodynamic radius • This quantity is less model dependent Bantle S. et al., Macromolecules, 1982, 15 (6)
- 48. Chain Conformation DLS/SLS: Coilto Globule Transition Sun S. et al., J. Chem. Phys. 73, 5971 (1980)
- 49. Kinetic Measurements: DLS SaltInduced Polystyrene Latex coagulation Fibrillogenesis, Aβ fibrils elongation rate 𝐼 Holthoff H., Langmuir, 1996, 12 (23) Lomakin A., PNAS 1996 93 (3) 1125-1129
- 50. Depolarized DLS: TobaccoVirus Rotational + Translational decorrelation rate Translational decorrelation rate • The instantaneous depolarized intensity depends on position and orientation • At short correlation times decorrelation is due to translation, at larger rimes to translation and rotation Wada A. Et al., J. Chem. Phys. 55, 1798 (1971)
- 51. Depolarized DLS: TobaccoVirus • Short time decorrelation rate dependence on q yields D • Long time decorrelation rate dependence on q yields rotational diffusion (given the value of D) • Rotational and translational diffusion coefficients yield tobacco mosaic virus dimensions: Wada A. Et al., J. Chem. Phys. 55, 1798 (1971)
- 52.
- 53. Traditional Solution: Dilution Limitations:Time consuming, sample composition is changed, limited applicability of methods Multiple Scattering
- 54.
- 55. 3D Cross-Correlation • Twosimultaneous scattering experiments with identical scattering volumes and vectors • Cross-correlation of the two signals suppresses multiply-scattered light Single Scattering: degenerate single Fourier component Multiple Scattering: different Fourier components Laser Sample in index matching vat Photon Detectors Cross Correlator Beam splitter Lens Lens Mirror y x z
- 56.
- 57. Laser Sample in index matchingvat Photon Detectors Cross Correlator Beam splitter Lens Lens Mirror Intensity Modulator Modulated 3D Cross-Correlation
- 58. Laser Sample in index matchingvat Photon Detectors Cross Correlator Beam splitter Lens Lens Mirror Intensity Modulator Modulated 3D Cross-Correlation
- 59.
- 60. Improved DLS Particle Sizingfor Turbid Samples 20 kHz Modulation, PS 100nm max
- 61. SLS for TurbidSamples Dilute Correct scattered intensity to get single scattering contribution Turbid - Modulated 3D DLS 10mm Round Cuvette, Monodisperse 430nm latex beads
- 62. SLS: Highly TurbidSuspensions of Small Particles 110nm latex spheres Intercept and pathlength- corrected Uncorrected
- 63. SLS for TurbidSamples: Square Cell Corrections I: intensity : cross-correlation intercept L: path length l: mean-free-path Square-cell -2 geometry: • minimizes path lengths • self-aligns scattering volume Turbidity correctionSingle scattering only
- 64. Thank you foryour attention!
Editor's Notes
- #2 add fourier space and natural space mention add contin and regularization method, integral diskretization, matrix inversion, problem, least square formulation, smoothness add a slide for spherical planar wave and wavevecror and it’s use to calculate phase shifts
- #15 Time dependent terms are dummy as they disappear when we calculate intensities
- #49 Key concept: R_g and R_h are weighted differently and depend differently on the chain conformation.. it’s clear that R_g is more sensitive as for R:h the solvent “penetrates” the loose expanded chain. When the chain is globule the difference is less marked as the macromolecule is a sphere : R_h = sqrt(3/5)R_g
- #54 interaction effects are lost if you dilute – crystallization, gelling, ageing, Calculated polydispersity is wrong by 1 order of magnitude and difficult to accurately fit size/index mention interactions can lead to increase of dynamics at high volume fractions, but these effects are an order of magnitude less. Also mention volume fraction here perhaps.
- #56 Only singly scattered light at the pricisely defined geometry yields correlated fluctuations - multiply scattered light does not have a common q vector for each detector. Suppression of 3 orders of magnitude. For multiple scattering, each detector is in general going to see a different q vector. Only single scattered light has a common q vector for the detector pairs and thus correlated. Fluctuations of different fourier components are statistically independent.
- #58 Emphasize ease of implementation, describe physically how this is implemented, including correlating at longer timescales. Undersampling.
- #59 Current limitations of switching speed is 1 MHz…1 us minimum lag time for correlation function.
- #61 Explain how our statistics get worse with multiple scattering. 3d is not doing magic, its simply extracting information that’s already there.
- #62 For borderline samples, we get better data. Enables more turbid samples and improved data. In form factor minimum single scattering intensity is very very small – we’re losing the data in the noise. Less than 5% single scattered light!!
- #63 Explain how our statistics get worse with multiple scattering. 3d is not doing magic, its simply extracting information that’s already there.