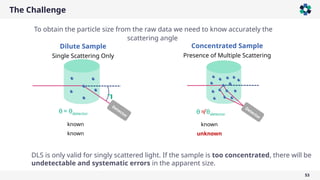
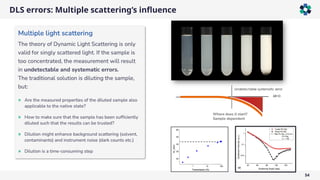
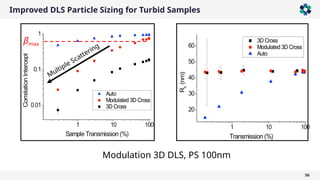
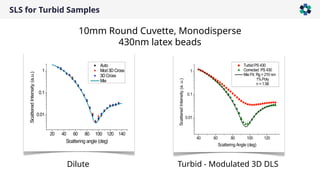
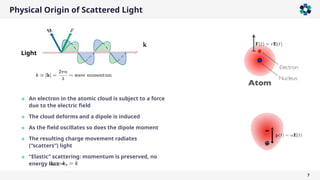
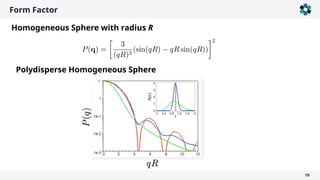
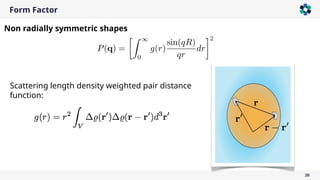
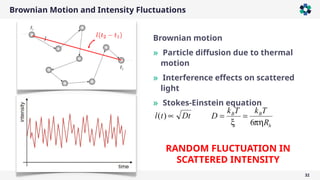
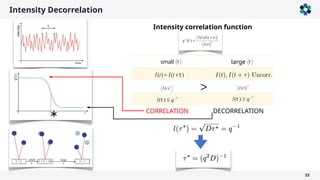
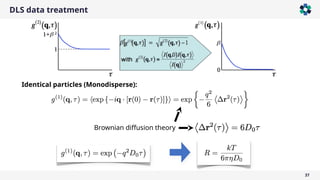
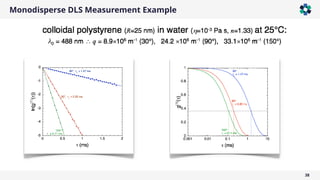
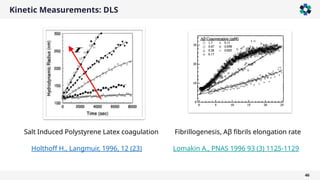
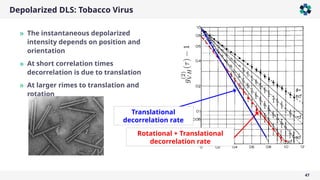
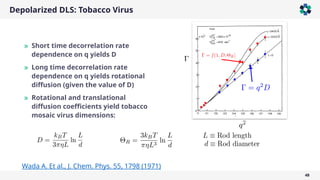
The document is a company presentation by Andrea Vaccaro focused on the fundamentals and applications of light scattering, particularly static light scattering (SLS) and dynamic light scattering (DLS). It covers theoretical aspects, practical implementations, and the challenges associated with analyzing concentrated systems, as well as advancements in measurement techniques for improved accuracy. Key topics include particle sizing, characterization of polymers and microgels, and the significance of scattering techniques in material science and nanotechnology.

1. Company presentation
Light Scattering Fundamentals
Andrea Vaccaro, PhD
Chief Technical Officer
LS Instruments AG

2. CONFIDENTIAL
Table of contents
2
» Part I: Theory Fundamentals
» Static Light Scattering (SLS)
» Dynamic Light Scattering (DLS)
» Part II: Applications
» Part III: Concentrated Systems

3. “Scattering” of Light
3
particle dispersion
wat
er

4. Light Scattering as Sizing Tool
4
Nanoparticles: 1-100 nm
Polymers, Macromolecules
Clays, Oxides, Proteins etc.

5. Company presentation
Light Scattering Fundamentals
Part I: Theory Fundamentals

6. Company presentation
Light Scattering Fundamentals
Static Light Scattering (SLS)

7. Physical Origin of Scattered Light
7
» An electron in the atomic cloud is subject to a force
due to the electric field
» The cloud deforms and a dipole is induced
» As the field oscillates so does the dipole moment
» The resulting charge movement radiates
(“scatters”) light
» “Elastic” scattering: momentum is preserved, no
energy loss ⇒
+
–
Light

8. A Collection of Atoms
8
Field scattered by a dipole of momentum
Spherical
Wave
Scattering
Geometry

9. A Collection of Atoms
9
By definition of polarizability
For an object smaller than λ (Clausius-Mossotti Relation):

10. A Collection of Atoms
10
Spherical
Wave
Contrast:
Ability to scatter
of the material
Piecing everything together:
Scattering
Geometry

11. Origin of the Scattering Contrast
11
» Interference
» For a larger object it is
possible to find a second
lump that scatters out of
phase and with the same
amplitude
» Completely destructive
interference
» For an infinite object it is
always possible to do this ⇒
No contrast

12. The Measured Quantity: the Scattered Intensity
12
» Whatever the detection technology, the observable quantity is not the
electric field but the flux of energy, the so-called light intensity
» It can be shown that in most conditions
» In practice the intensity fluctuates
in time
» In SLS experiment the average
intensity is measured

13. RGD Theory
13
» Assumption: The field inside the particle is the
incident field
» To satisfy this assumption we must require for the
incident field:
i. no reflection at the particle/solvent interface
ii. no phase change within the particle
» Every small lump in the particle scatters as if it were “alone”

14. RGD Interference: The Scattering Vector
14
Interference
Term
Dropping the dummy time dependency
terms:

15. Light Scattering as Sizing Tool
15
The module of the scattering vector has dimensions of inverse of length:
1/q is the length-scale of the interference phenomenon.
Two material lumps farther than 1/q interfere destructively.
Closer than 1/qinterfere additively
Destructive
Interference, Smaller
Intensities
No internal
Interference
Maximum Intensity
1/q can be interpreted as a
rough measure of the probed
length-scale

16. One Particle: The Scattering Amplitude
16
Integrating previous equation over the whole particle:
Labeling the particle with the subscript j and factoring out its position by means the variable
substitution
We obtain
Particle j scattering
amplitude
Interference : Particle
Position
Internal
Interference

17. An Ensemble of Particles
17
Previous result allows to sum each contribution
= 0 = 0
!
Independent position and orientation
We measure a time average:

18. RGD Scattered Intensity
18
» The electric field in not an observable
» But intensity is:
Average
Contrast
Structure
Factor:
Interparticle
Interference
Form Factor:
Intraparticle
Interference
Scattering Geometry
» The RGD assumption results in the factorization of different
contributions
» Similar factorization for polydisperse systems
After many manipulations:

19. Form Factor
19
Homogeneous Sphere with radius R
Polydisperse Homogeneous Sphere

20. Form Factor
20
Non radially symmetric shapes
Scattering length density weighted pair distance
function:

21. Form Factor at Small q: The Radius of Gyration
21
Expanding in series the interference factor...
The form factor becomes
Radius of Gyration:
In a plot of the intensity vs. q2
the extrapolation to zero yields a size parameter that is model
independent

22. Radius of Gyration: Polydisperse Case
22
𝑅𝑔
2
≡
∫ 𝑓 (𝑅)𝑉 ( 𝑅)2
𝑅𝑔
2
𝑑𝑅
∫ 𝑓 ( 𝑅)𝑉 (𝑅)2
𝑑𝑅
𝑉 (𝑅)≡Volume of a particle with size 𝑅
𝑓 (𝑅)≡fraction of the particle population with size 𝑅

23. Form Factor
23
Polymers

24. The Structure Factor
24
In the same vein as the form factor it can be shown that accounting only for pair
interactions (“on the pair level”)
Applying the Ergodic Hypothesis:

25. The Rayleigh Ratio
25
Scattered Intensity:
The Rayleigh Ratio: Scattered intensity per unit incident intensity, unit solid angle,
and unit scattering volume.
Depends only on the thermodynamic state of the solvent not on the measuring
apparatus
Mass
Concentration
Sample
Contrast
Molar
Mass
Instrumental
Constant
Solvent
Scattering
(Background)

26. Absolute Measurements
26
» Knowledge of the constant A enables absolute intensity measurements
» Absolute measurements allow for the determination of the radius of gyration and
the second virial coefficient but also of the molar mass M, or the particle
concentration
» How do we do it?
Excess Rayleigh Ratio:

27. Absolute Measurements: How
27
» Scientists have built special devices that allow the measurement of
Rayleigh ratios, values for common reference solvents are available in
literature
» If we measure the same reference solvent in the same thermodynamic
conditions, we have:
Substituting back:

28. Data Treatment and Absolute Intensity
28
M
R2
g/3
Polydisperse Case:
Experimental
Data
Data
Modeling

29. Company presentation
Light Scattering Fundamentals
Dynamic Light Scattering (DLS)

30. Intensity Fluctuation
30
1.6 mm
0.12 mm

31. Particle Dynamics in Real and Reciprocal Space
31
Particle tracking with a microscope
Dynamics in reciprocal (Fourier) space

32. Brownian Motion and Intensity Fluctuations
32
Brownian motion
» Particle diffusion due to thermal
motion
» Interference effects on scattered
light
» Stokes-Einstein equation
RANDOM FLUCTUATION IN
SCATTERED INTENSITY

33. Intensity Decorrelation
33
Intensity correlation function
∗
small large
CORRELATION DECORRELATION
>

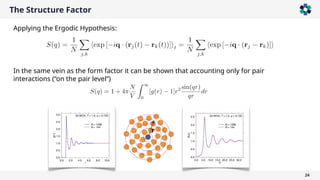
34. Field Correlation Function
34
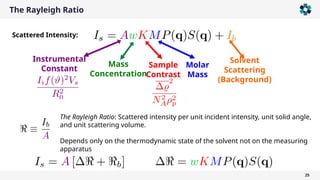
Upon normalization:
Identical Independent
Particles
It can be modeled, but cannot be measured!
The electric field correlation function is important as it is directly connected
to colloid dynamics models
∑
𝑗 ,𝑘
𝐹 𝑗 (𝑞)𝐹𝑘
∗
(𝑞)exp{−𝑖𝒒⋅[𝒓 𝑗 (0)−𝒓𝑘 (𝜏)]}
⟨𝐸(𝒒,0)𝐸
∗
(𝒒,𝜏)⟩ ∑
𝑗,𝑘
𝐹𝑗 (𝑞)exp{−𝑖𝒒⋅𝒓 𝑗 (0)}ℑ(𝐹𝑘(𝑞)exp{−𝑖𝒒⋅𝒓𝑘 (𝜏)})

35. Intensity Correlation Function
35
After many manipulations
As for SLS we can measure the intensity correlation function
Omitting the scattering amplitudes Fj :

36. Coherence Area, Siegert Relationship
36
» In practical implementations the field is not always a
Gaussian stochastic variable
» This happens since we sometimes image more than one
coherence area (“speckle”)
» The signal to noise ratio is lowered

37. DLS data treatment
37
Identical particles (Monodisperse):
Brownian diffusion theory

38. Monodisperse DLS Measurement Example
38

39. Polydisperse Particles: Cumulant Analysis
39
Intensity weighted correlation function
Cumulant Expansion:
Typical uncertainty in cv is ± 0.02, i.e. it is hard to determine cv 0.2 (20%)
≤
For a polydisperse sample
Intensity weighted diffusion coefficient

40. Polydisperse Particles: Cumulant Analysis
40
Two species, differing in size by 50%

41. Company presentation
Light Scattering Fundamentals
Part II: Applications

42. Static Properties: Zimm Plot
42
Schmidt M., Macromolecules, 1984, 17 (4)

43. Polymer Properties: Interaction and Conformation
43
At the Theta temperature the chain follows the Gaussian chain model, the
second virial coefficient is close but not equal to zero
Berry G. C., J. Chem. Phys. 44, 4550 (1966)

44. Dynamic Properties: DLS Zimm Plot
44
» Hydrodynamic Radius depends through a certain scattering/colloid dynamic model
on the scattering angle
» DLS Zimm Plot enables the determination of the zero angle, no interactions
hydrodynamic radius
» This quantity is less model dependent
Bantle S. et al., Macromolecules, 1982, 15 (6)

45. Chain Conformation DLS/SLS: Coil to Globule Transition
45
Sun S. et al., J. Chem. Phys. 73, 5971 (1980)
Temperature

46. Kinetic Measurements: DLS
46
Salt Induced Polystyrene Latex coagulation Fibrillogenesis, Aβ fibrils elongation rate
𝐼
Holthoff H., Langmuir, 1996, 12 (23) Lomakin A., PNAS 1996 93 (3) 1125-1129

47. Depolarized DLS: Tobacco Virus
47
Rotational + Translational
decorrelation rate
Translational
decorrelation rate
» The instantaneous depolarized
intensity depends on position and
orientation
» At short correlation times
decorrelation is due to translation
» At larger rimes to translation and
rotation

48. Depolarized DLS: Tobacco Virus
48
» Short time decorrelation rate
dependence on q yields D
» Long time decorrelation rate
dependence on q yields rotational
diffusion (given the value of D)
» Rotational and translational
diffusion coefficients yield tobacco
mosaic virus dimensions:
Wada A. Et al., J. Chem. Phys. 55, 1798 (1971)

49. Microgel Characterization
49
» Capture/Release of small agents (small molecules,
drugs
» Viscoelastic properties (thickener, hydraulic damping
etc.)
» Catalysis, Oil recovery, Nano Reactors
» Control of colloidal stability
» Tunable optical/magnetic properties sensors,
→
switches
» Hydrogel opals, Hu, Lu & Gao, J. Adv. Mat (2001)
The fuzzy sphere model

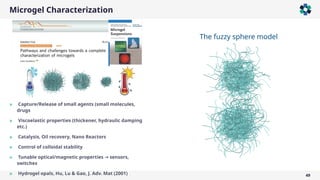
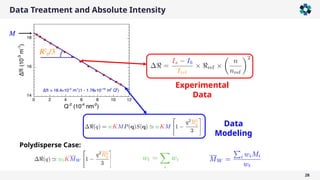
50. Microgel Characterization
50
Δ 𝜌 (𝑟 )∝ ∫
− ∞
∞
Θ [𝑥 − 𝑅 ] 1
𝜎 √2 𝜋
𝑒
−
(𝑟 −𝑥 )
2
2 𝜎
2
𝑑𝑥=
1
2
erfc
[𝑟 − 𝑅
√2 𝜎 ]
𝑃 (𝑞) ∝
3[sin (𝑞𝑅)−𝑞𝑅 cos(𝑞𝑅)]
(𝑞𝑅)
3
exp[−
(𝜎 𝑞)2
2 ]
*M. Stieger, W. Richtering, J. S. Pedersen, and P. Lindner, Small-angle neutron scattering study of structural
changes in temperature sensitive microgel colloids, The Journal of Chemical Physics 120, 6197 (2004). More
than 500 citations.
‘Smeared’ density profile
𝑟 [nm ]
𝜌 (𝑟 )[arb. u]
𝑟 [nm ]
sphere
Fuzzy
sphere
𝜌 (𝑟 )[arb. u]
The fuzzy sphere model

51. Microgel Characterization: Microgel Results
51
5
1
𝐼 (𝑞)
𝐼 (𝑞)
𝐼 (𝑞)
𝐼 (𝑞)
Microgel Swelling and Rheology - F. Scheffold in collaboration
with J.L. Harden (Ottawa), E. Zaccarelli (Rome), Sakai Takamasa
(Japan)

52. Company presentation
Light Scattering Fundamentals
Part III: Concentrated Systems

53. The Challenge
53
Detector
Dilute Sample
Single Scattering Only
Concentrated Sample
Presence of Multiple Scattering
Detector
θ = θdetector

DLS is only valid for singly scattered light. If the sample is too concentrated, there will be
undetectable and systematic errors in the apparent size.
θ ≠ θdetector
Detector
To obtain the particle size from the raw data we need to know accurately the
scattering angle
known
known
known
unknown

54. DLS errors: Multiple scattering’s influence
54

55. Modulated 3D DLS
Filter for multiple scattering suppression
55
How does it work?
» Two concurrent DLS measurements on same
scattering volume and at same scattering angle
» Outputs of the two measurements are cross-
correlated
» Multiple scattering information is different
between two outputs, thereby uncorrelated and
suppressed
» Single scattering information is common across
the two measurements and passes through to
standard DLS analysis
» Modulated 3D Cross-Correlation temporally
isolates the two measurements (patented)
Accurate measurements for turbid samples, and full
confidence regardless of sample dilution. The result
is guaranteed to be free of multiple scattering.
Block, I. and Scheffold, F., Modulated 3D cross-correlation light scattering: improvin
g turbid sample characterization,
Review of Scientific Instruments 81, 123107 (2010)

56. Improved DLS Particle Sizing for Turbid Samples
56
Modulation 3D DLS, PS 100nm
Multiple Scattering
βmax

57. SLS for Turbid Samples
Dilute
Correct scattered
intensity to get single
scattering
contribution
Turbid - Modulated 3D DLS
10mm Round Cuvette, Monodisperse
430nm latex beads

58. Modulated 3D Cross-Correlation DLS
accurate particle sizing without dilution
58
Benefits and outlook
» Eliminate dilution, increase
throughput and sample recovery
» Ensure measured properties are
representative of native sample
» Improve early prediction of
formulation stability
» Enable new approaches including in-
vial non-destructive advanced QC
0.1 1
0
5
10
15
20
25
30
35
40
45
50
Modulated 3D DLS
Standard Backscattering DLS
Volume Fraction (% v/v)
Particle
Sizing
Error
(%)
Measurements of a commercial nanoemulsion adjuvant
(Addavax™), using both a standard DLS instrument and
one with the Modulated 3D DLS approach
5

59. Contact us
LS Instruments AG
Passage du Cardinal 1 1700 Fribourg Switzerland
www.lsinstruments.ch
GENERAL
+41 (0)26 422 24 29
info@lsinstruments.c
h
SALES
+41 (0)26 508 54 98
sales
@lsinstruments.ch
SUPPORT
+41 (0)26 508 54 24
support
@lsinstruments.ch