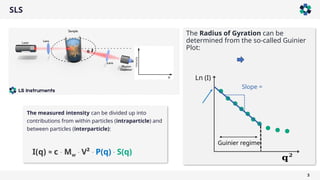
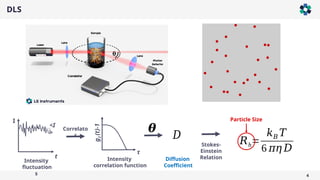
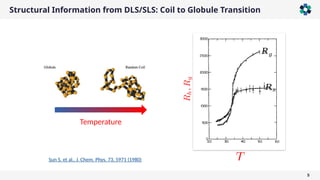
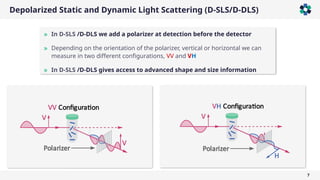
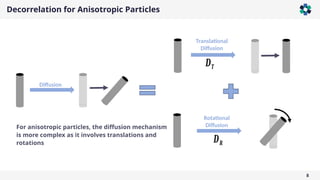
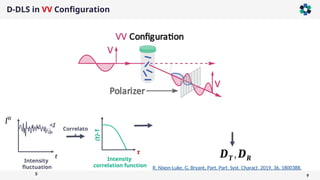
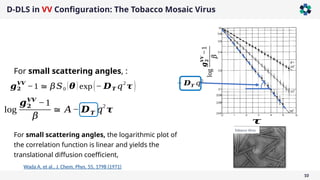
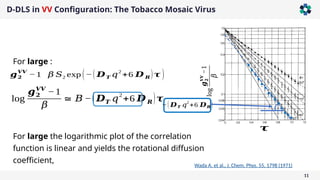
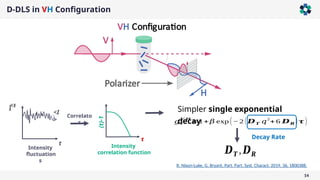
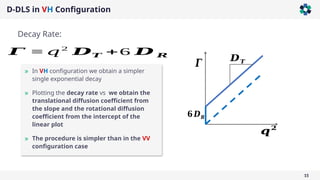
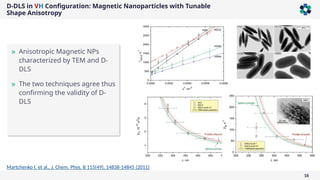
The document presents a comprehensive overview of light scattering techniques used for characterizing the shape and size of colloidal particles, particularly focusing on dynamic and static light scattering (DLS/SLS). It discusses the advantages of DLS, such as its speed and non-destructive nature, and elaborates on methods to obtain detailed shape information using depolarized configurations. Key findings include the ability to derive translational and rotational diffusion coefficients, which further allow for the characterization of anisotropic particles like the tobacco mosaic virus and magnetic nanoparticles.

1. Company presentation
Shape Characterization Using
Dynamic & Static Light
Scattering
Andrea Vaccaro PhD, CTO
LS Instruments AG

2. In SLS/DLS, a laser beam is sent through a colloidal sample, the average scattered intensity and the
auto/cross correlation of the resulting scattered light are computed.
Why choose DLS as a characterization method?
• Fast
• Simple measurements with easy sample preparation
• In-situ, non-destructive approach
Measuring particle size reliably
2
Static and Dynamic Light Scattering (SLS/DLS)
𝜽

3. 3
SLS
The measured intensity can be divided up into
contributions from within particles (intraparticle) and
between particles (interparticle):
I(q) ≈ c ∙ Mw ∙ V² ∙ P(q) ∙ S(q)
The Radius of Gyration can be
determined from the so-called Guinier
Plot:
Slope =
Ln (I)
Guinier regime
𝐪𝟐

4. DLS
4
Intensity
fluctuation
s
I
t
<I
> 𝜽
𝐷
Diffusion
Coefficient
𝑅h=
𝑘𝐵 𝑇
6 𝜋𝜂 𝐷
Stokes-
Einstein
Relation
Particle Size
Intensity
correlation function
g
2
(t)-1
τ
Correlato
r

5. Structural Information from DLS/SLS: Coil to Globule Transition
5
Sun S. et al., J. Chem. Phys. 73, 5971 (1980)
𝑅h
𝑅𝑔
Temperature

6. Shape from DLS/SLS
6
Can we get detailed shape and size information
from SLS/DLS?

7. 7
Depolarized Static and Dynamic Light Scattering (D-SLS/D-DLS)
» In D-SLS /D-DLS we add a polarizer at detection before the detector
» Depending on the orientation of the polarizer, vertical or horizontal we can
measure in two different configurations, VV and VH
» In D-SLS /D-DLS gives access to advanced shape and size information

8. Decorrelation for Anisotropic Particles
8
Diffusion
Translational
Diffusion
𝑫𝑻
Rotational
Diffusion
𝑫𝑹
For anisotropic particles, the diffusion mechanism
is more complex as it involves translations and
rotations

9. D-DLS in VV Configuration
9
Intensity
fluctuation
s
𝑰𝑽𝑽
t
<I
>
Intensity
correlation function
(t)-1
τ
Correlato
r
𝑫𝑻 , 𝑫𝑹
R. Nixon-Luke, G. Bryant, Part. Part. Syst. Charact. 2019, 36, 1800388.

10. D-DLS in VV Configuration: The Tobacco Mosaic Virus
10
For small scattering angles, :
𝒈𝟐
𝑽𝑽
−1≅ 𝛽𝑆0 (𝜽 ) exp(− 𝑫𝑻 𝑞2
𝝉 )
log
𝒈𝟐
𝑽𝑽
−1
𝛽
≅ 𝐴− 𝑫𝑻 𝑞
2
𝝉
log
𝒈
𝟐
𝑽𝑽
−1
𝛽
𝝉
For small scattering angles, the logarithmic plot of
the correlation function is linear and yields the
translational diffusion coefficient,
− 𝑫𝑻 𝑞2
Wada A. et al., J. Chem. Phys. 55, 1798 (1971)
Tobacco Virus

11. D-DLS in VV Configuration: The Tobacco Mosaic Virus
11
log
𝒈
𝟐
𝑽𝑽
−1
𝛽
𝝉
For large :
𝒈𝟐
𝑽𝑽
−1 𝛽 𝑆2 exp (−( 𝑫𝑻 𝑞
2
+6 𝑫 𝑹)𝝉 )
log
𝒈𝟐
𝑽𝑽
−1
𝛽
≅ 𝐵 −(𝑫𝑻 𝑞
2
+6 𝑫 𝑹)𝝉
−(𝑫𝑻 𝑞
2
+6 𝑫𝑹)
For large the logarithmic plot of the correlation
function is linear and yields the rotational diffusion
coefficient,
Wada A. et al., J. Chem. Phys. 55, 1798 (1971)

12. Shape and Size from Diffusion Coefficients
For an axisymmetric particle of major size, , minor size, ,
and anisotropy factor
𝑫𝑻 , 𝑫𝑹
Microhydrodynami
cs
𝑳,𝒅,𝒑
For rodlike particles, such as Tobacco Mosaic Virus:
𝑫 𝑹=
1
3
𝑘𝑇 (ln 𝒑 𝑪 𝑹)
𝜋 𝜂0 𝑳
3
𝑫𝑻 =
1
3
𝑘𝑇 (ln 𝒑 𝑪𝑻 )
𝜋 𝜂0 𝑳
𝑪𝑻 =0.312+
0.565
𝒑
+
0.100
𝒑
𝟐
𝑪𝑹=−0.662+
0.917
𝒑
−
0.050
𝒑
𝟐
Ortega A.; Garc a
ı́ de la Torre J., J. Chem. Phys. 119, 9914–9919 (2003)
Shape and Size
𝑳
𝒅

13. Takeaways
» In VV Configuration at low angles DLS provides access to the
translational diffusion of anisotropic particles
» At large angles and large lag times, knowing the
translational diffusion coefficient, we can obtain the
rotational diffusion coefficient
» From translational and rotational diffusion coefficients we
can obtain size and shape parameters of anisotropic
particles
» The procedure is complicated by the fact that in general
correlation functions display an angle-dependent double
decay

14. D-DLS in VH Configuration
14
Intensity
fluctuation
s
𝑰𝑽 𝑯
t
<I
>
Intensity
correlation function
(t)-1
τ
Correlato
r
𝑫𝑻 , 𝑫𝑹
𝑔2
𝑽 𝑯
=1+ 𝛽 exp (−2 (𝑫𝑻 𝑞
2
+ 6 𝑫𝑹 )𝝉)
Simpler single exponential
decay
R. Nixon-Luke, G. Bryant, Part. Part. Syst. Charact. 2019, 36, 1800388.
Decay Rate

15. D-DLS in VH Configuration
15
𝜞 ≡ 𝑞2
𝑫𝑻 +6 𝑫 𝑹
» In VH configuration we obtain a simpler
single exponential decay
» Plotting the decay rate vs we obtain the
translational diffusion coefficient from
the slope and the rotational diffusion
coefficient from the intercept of the
linear plot
» The procedure is simpler than in the VV
configuration case
Decay Rate:
𝟔 𝑫𝑹
𝑫𝑻
𝒒𝟐
𝜞

16. D-DLS in VH Configuration: Magnetic Nanoparticles with Tunable
Shape Anisotropy
16
» Anisotropic Magnetic NPs
characterized by TEM and D-
DLS
» The two techniques agree thus
confirming the validity of D-
DLS
Martchenko I. et al., J. Chem. Phys. B 115(49), 14838-14845 (2011)

17. Contact us
LS Instruments AG
Passage du Cardinal 1 1700 Fribourg Switzerland
www.lsinstruments.ch