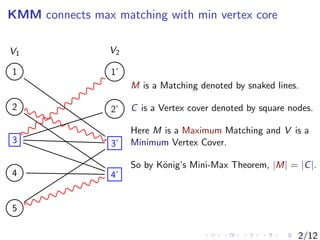
The document presents a study on combinatorial matrix theory, focusing on the connection between maximum matching and minimum vertex covers through the Kőnig-Menger-Maxwell theorem. It introduces a formal language for min-max reasoning and demonstrates the equivalence of fundamental theorems in graph theory, including Menger's theorem, Hall's theorem, and Dilworth's theorem. The authors also discuss potential future work, including the relationship between KMM and Pigeonhole Principle, and the ability of their formalism to prove complex matrix identities.

1. Feasible Combinatorial Matrix Theory
Ariel G. Fern´andez, Michael Soltys.
fernanag@mcmaster.ca, soltys@mcmaster.ca
Department of Computing and Software
McMaster University
Hamilton, Ontario, Canada

2. Outline
Introduction
KMM connects max matching with min vertex core
Language to Formalize Min-Max Reasoning
Main Results
LA with ΣB
1 -Ind. proves KMM
LA Equivalence: K¨onig, Menger, Hall, Dilworth
Related Theorems
Menger’s Theorem, Hall’s Theorem, and Dilworh’s Theorem
Future Work
1/12

3. KMM connects max matching with min vertex core
1
2
3
4
5
1’
2’
3’
4’
V1 V2
2/12

4. KMM connects max matching with min vertex core
1
2
3
4
5
1’
2’
3’
4’
V1 V2
M is a Matching denoted by snaked lines.
C is a Vertex cover denoted by square nodes.
Here M is a Maximum Matching and V is a
Minimum Vertex Cover.
So by K¨onig’s Mini-Max Theorem, |M| = |C|.
2/12

5. Language to Formalize Min-Max Reasoning
LA is
(Developed by Cook and Soltys.) Part of Cook’s program of
Reverse Mathematics.
Three sorts:
indices
ring elements
matrices
LA formalize linear algebra (Matrix Algebra).
LA over Z (though all matrices are 0-1 matrices.)
Since we want to count the number of 1s in A by ΣA.
3/12

6. LA with ΣB
1 -Induction
LA (i.e., LA with ΣB
0 -Induction), proves all the ring properties of
matrices (eg.,(AB)C = A(BC)), and LA over Z translates into
TC0
-Frege ([Cook-Soltys’04]).
Bounded Matrix Quantifiers: We let
(∃A ≤ n)α stands for (∃A)[|A| ≤ n ∧ α], and
(∀A ≤ n)α stands for (∀A)[|A| ≤ n → α].
LA with ΣB
1 -Induction correspond to polytime reasoning and proves
standard properties of the determinant, and translate into extended
Frege.
4/12

7. Main Results
Theorem 1:
LA with ΣB
1 -Induction KMM.
Theorem 2:
LA proves the equivalence of fundamental theorems:
K¨onig Mini-Max
Menger’s Connectivity
Hall’s System of Distinct Representatives
Dilworth’s Decomposition
5/12

8. LA with ΣB
1 -Ind. proves KMM
Diagonal Property
∗
∗
0
...
00
0
0 . . .1
Either Aii = 1 or (∀j ≥ i)[Aij = 0 ∧ Aji = 0].
Claim Given any matrix A, ∃LA proves that there exist permutation
matrices P, Q such that PAQ has the diagonal property.
6/12

9. LA Equivalence: K¨onig, Menger, Hall, Dilworth
Theorem :
LA proves the equivalence of fundamental theorems:
K¨onig Mini-Max
Menger’s Connectivity
Hall’s System of Distinct Representatives
Dilworth’s Decomposition
7/12

10. Menger’s Connectivity Theorem – Example
y
a d
ex b
c f
x y

11. Menger’s Connectivity Theorem – Example
y
a d
ex b
c f
x y
8/12

12. Menger’s Connectivity Theorem – Example
y
a d
ex b
c f
x y
8/12

13. Menger’s Connectivity Theorem – Example
y
a d
ex b
c f
x y
8/12

14. Menger’s Connectivity Theorem – Example
y
a d
ex b
c f
x y
8/12

15. Hall’s SDR Theorem - Example
Let X = {1, 2, 3, 4, 5} be the 5-set of integers.
Let S = {S1, S2, S3, S4} be a family of X. For instance,
S1 = {2, 5}, S2 = {2, 5}, S3 = {1, 2, 3, 4}, S4 = {1, 2, 5}.
Then D := (2, 5, 3, 1) is an SDR for (S1, S2, S3, S4).
Now, if we replace S4 by S4 = {2, 5}, then the subsets no
longer have an SDR.
For S1 ∪ S2 ∪ S4 is a 2-set, and three elements are required to
represent S1, S2, S4
9/12

16. Dilworth’s Decomposition Theorem - Example
{}
{1} {2} {3}
{1, 2} {1, 3} {2, 3}
{1, 2, 3}
Let P = (⊂, 2X
), i.e., all subsets of
X with |X| = n with set inclusion,
x < y ⇐⇒ x ⊂ y.
(A) Suppose that the largest
chain in P has size . Then P can
be partitioned into antichains.
We have 4-antichains [{}] ,
[{1}, {2}, {3}] , [{1, 2}, {1, 3}, {2, 3}] ,
and [{1, 2, 3}] .
(B) Suppose that the largest
antichain in P has size .
Then P can be partitioned into
disjoint chains. We have
[{} ⊂ {1} ⊂ {1, 2} ⊂ {1, 2, 3}] ,
[{2} ⊂ {2, 3}] , and [{3} ⊂ {1, 3}].
10/12

17. Examples of LA formalization
For example, concepts necessary to state KMM in LLA:
Cover(A, α) :=
∀i, j ≤ r(A)(A(i, j) = 1 → α(1, i) = 1 ∨ α(2, j) = 1)
Select(A, β) :=
∀i, j ≤ r(A)((β(i, j) = 1 → A(i, j) = 1)
∧
∀k ≤ r(A)(β(i, j) = 1 → β(i, k) = 0 ∧ β(k, j) = 0))
11/12

18. Future Work
Can LA-Theory prove KMM?
What is the relationship between KMM and PHP?
(Eg. LA ∪ PHP KMM?)
Can LA ∪ KMM prove Hard Matrix Identities?
We would like to know whether LA ∪ KMM can prove hard
matrix identities, such as AB = I → BA = I. Of course, we
already know from [TZ11] that (non-uniform) NC2
-Frege is
sufficient to prove AB = I → BA = I, and from [Sol06] we
know that ∃LA can prove them also.
What about ∞-KMM?
12/12