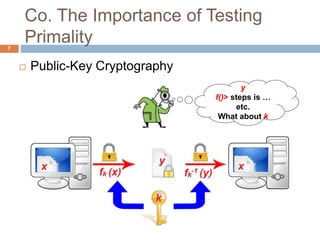
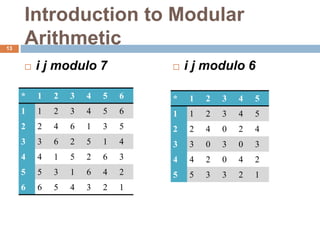
This document discusses the complexity of primality testing. It begins by explaining what prime and composite numbers are, and why primality testing is important for applications like public-key cryptography that rely on the assumption that factoring large composite numbers is computationally difficult. It then covers algorithms for primality testing like the Monte Carlo algorithm and discusses their runtime complexities. It shows that while testing if a number is composite can be done in polynomial time, general number factoring is believed to require exponential time, making primality testing an important problem.

1. THE COMPLEXITY OF
PRIMALITY TESTING
Presented By:
Mohammad Elsheikh Salim Elsheikh
lecturer - Shendi University (Sudan)
Mohammad_elgarrai@yahoo.com
Supervision of:
DR.Mohammed El-Hafiz
‫الرحيم‬ ‫الرحمن‬ ‫هللا‬ ‫بسم‬
SUDAN UNIVERSITY OF SCIENCE AND
TECHNOLOGY
COLLEGE OF COMPUTER SCIENCE AND
INFORMATION TECHNOLOGY
PHD 4

2. SEMINAR OBJECTIVES
2
 SEMINAR OBJECTIVES
 Explaining Primality Testing Problem.
 Why Primality Testing is important .
 Which Field required it.
 Algorithm that can solve this problem and it
complexity classes.

3. Introduction
 Prime numbers have attracted much attention
from mathematicians for many centuries.
 However, the first actual use of prime numbers
in an important area outside of the theory of
numbers was discovered only in the mid to
late 1900s.
 This was in the establishment of a technical
system to be used in maintaining the secrecy
of electronic communications.

4. Definition
 Factor: when two or more numbers are multiplied,
each number is called a factor of the product. 6 =
2 * 3
 Prime number: is a whole number greater than 1
that has exactly two positive factors, 1 and itself.
Example :
 2, 3, 5, 7, 11, 13, and 17.
 Composite number: is a whole number that has
more than two positive factors. Example: 4, 6,
8….
 504 is composite, and its prime factorization is
 23 x 32 x 7.
 0 and 1 > Neither prime nor composite.

5. The Importance of Testing
Primality5
 Primality testing are essential ingredients in
computer-security systems.
 There are a number of techniques that
enhance computer security, rely on the
assumption that it is hard to factor
numbers, that is, given a composite
number, to find its prime factors.

6. The Importance of Testing
Primality6
 In particular, these schemes, based on what
are called RSA codes, use integers of, say,
128 bits that are the product of two primes,
each of about 64 bits.
 Two scenarios to explain it:
 Public-Key Cryptography
 Public-Key Signatures

7. Co. The Importance of Testing
Primality7
 Public-Key Cryptography
y
f()> steps is …
etc.
What about k

8. Co. The Importance of Testing
Primality8
 Public-Key Signatures

9. Co. The Importance of Testing
Primality9
 Both scenarios above are believed to work
and to be secure, in the sense that it really
does take exponential time to factor the
product of two large primes:
1. The construction of public keys requires that
we be able to find large primes quickly.
2. The security depends on there being no
polynomial way to factor in general.

10. Introduction to Modular
Arithmetic10
 First we explain what is the Remainders.
 Given two integers a and b, as long as b ≠ 0, we
can find q (quotient) and r (remainder), such that
a =q*b + r.
 Let’s let b = 5.
• 0 = 0*5 + 0
• 1 = 0*5 + 1
• 2 = 0*5 + 2
• 3 = 0*5 + 3
• 4 = 0*5 + 4
• 5 = 1*5 + 0
• 6 = 1*5 + 1
• 7 = 1*5 + 2
• 8 = 1*5 + 3
• 9 = 1*5 + 4
• 10 = 2*5 + 0
.
.
.
.
.

11. What is modular arithmetic?
 Arithmetic with the remainders upon division
by a fixed number n.
 It is based upon the idea that the remainder of
the sum / difference / product of two numbers
is the remainder of the sum / difference /
product of the remainders.
 For example, if n=5,
 (31+7)%5 = 38%5 = 3, and
 (31%5+7%5)%5 = (1+2 )%5 =3

12. Introduction to Modular
Arithmetic12
 Example: Suppose p = 13 Then
 3 + 5 ≡13 8 <=> (3 + 5) modulo 13 = 8
 7 + 10 ≡13 4.
o 7 + 10 = 17 => 17 > 13 => 17-13 = 4
 -5 ≡13 8.
o 13 – 5 = 8 => 8 < 13
 11- 4 ≡13 7
 4 - 11 ≡13 6.
o 4 - 11 = -7 => no negative so we must add 13 to get 6.

13. Introduction to Modular
Arithmetic
 i j modulo 7  i j modulo 6
13
* 1 2 3 4 5 6
1 1 2 3 4 5 6
2 2 4 6 1 3 5
3 3 6 2 5 1 4
4 4 1 5 2 6 3
5 5 3 1 6 4 2
6 6 5 4 3 2 1
* 1 2 3 4 5
1 1 2 3 4 5
2 2 4 0 2 4
3 3 0 3 0 3
4 4 2 0 4 2
5 5 3 3 2 1

14. Introduction to Modular
Arithmetic14
 Some useful facts, which we shall not prove
here are:
 If p is a prime, then ap-1 = 1 modulo p. This
statement is called Fermat’s theorem.
 The degree of a modulo a prime p is always a
divisor of p - 1.
 If p is a prime, there is always some a that has
degree p - 1 modulo p.

15. The Complexity of Modular-
Arithmetic Computations15
 Compute modulo some prime p, and the binary
representation of p is n-bits long; i.e., p itself is
around 2n.
 The running time of a computation is stated in
terms of n, the input length, rather than p, the
“value” of the input. For Instance, counting up
to p takes time O(2n),
 Will not be polynomial-time, as a function of n.

16. The Complexity of Modular-
Arithmetic Computations16
 Add two numbers modulo p in O(n) time on a
typical computer or multitape TM.
 Recall that we simply add the binary numbers,
and if the result is p or greater, then subtract p.
 Likewise, we can multiply two numbers in
O(n2) time, either on a computer or a Turing
machine.
 After multiplying the numbers in the ordinary
way, and getting a result of at most 2n-bits, we
divide by p and take the remainder.

17. The Complexity of Modular-
Arithmetic Computations17
 Raising a number x to an exponent is trickier,
since that exponent may itself be exponential
in n.
 Since p - 1 is around 2n , if we were to multiply
x by itself p - 2 times, we would need O(2n)
multiplications, and even though each
multiplication involved only n-bit numbers and
could be carried out in O(n2) time,
 The total time would be O(n22n), which is not
polynomial in n.

18. The Complexity of Modular-
Arithmetic Computations18
 Fortunately, there is a “recursive-doubling”
trick that lets us compute xp-1 in time that is
polynomial in n:
1. Compute the at most n exponents x,x2,x4,x8,... ,
until the exponent exceeds p - 1. Each value is
an n-bit number that is computed in O(n2) time
by squaring the previous value in the sequence,
so the total work is O(n3).
2. Find the binary representation of p - 1, say
p - 1 = an-1 … a1a0. We can write:

19. The Complexity of Modular-
Arithmetic Computations19
 where each aj is either 0 or 1. Therefore,
 which is the product of those values for
which aj=1. Since we computed each of those
s in step (1), and each is an n-bit number,
we can compute the product of these n or
fewer numbers in O(n3) time.
 Thus, the entire computation of xp-1 takes
O(n3) time.

20. Random-Polynomial Primality
Testing20
 The method actually used to generate n-bit
primes is to pick an n-bit number at random
and apply the Monte-Carlo algorithm to
recognize composite numbers some large
number of times, say 50.
 If any test says that the number is composite,
then we know it is not a prime. If all 50 fail to
say that it is composite, there is no more than
250 probability that it really is composite.
 Thus, we can fairly safely say that the number
is prime and base our secure operation on that
fact.

21. Random-Polynomial Primality
Testing21
 Monte - Carlo algorithm for the composite
numbers:
1. Pick an x at random in the range 1 to p - 1.
2. Compute xp-1 modulo p. Note that if p is an n-
bit number, then this calculation takes O(n3)
time
3. If xp-1 ≠ 1 modulo p, accept; x is composite.
Otherwise, halt without accepting.
* If p is prime, then xp-1 = 1 modulo p, so we
always halt without accepting;

22. Random-Polynomial Primality
Testing22
 Carmichael numbers:
 The smallest Carmichael number is 561, That
is, one can show x560 = 1 modulo 561 for all x
that are not divisible by 3, 11, or 17,
 Even though 561 = 3 x 11 x 17 is evidently
composite.
 Thus, we shall claim, but without a complete
proof, that:
 Theorem : The set of composite numbers is in
RP.

23. Random-Polynomial Primality
Testing23
 Can We Factor in Random Polynomial Time?
 The previous algorithm may tell us that a number
is composite, but does not tell us how to factor the
composite number.
 It is believed that there is no way to factor
numbers, even using randomness, that takes
only polynomial time, or even expected
polynomial time.
 If that assumption were incorrect, then the
applications that we discussed would be insecure
and could not be used.

24. Nondeterministic Primality
Tests24
 That the language of primes is in NP ∩ co-NP.
 Therefore the language of composite numbers,
the complement of the primes, is also in NP ∩
co-NP.
 The case is that the primes or the composite
numbers are not NP-complete, for if either
were true then we would have the unexpected
equality NP = co-NP.
 One part is easy:
 The composite numbers are obviously in NP,
so the primes are in co-NP. We prove that fact

25. Nondeterministic Primality
Tests25
 Theorem: The set of composite numbers is in NP.
 PROOF;
 The nondeterministic, polynomial-time algorithm for the composite
numbers is:
 Step one:
 Take p as an n-bit number p,
 Guess a factor f of at most n-bits.
 f ≠ 1 and f ≠ p.
 The time taken by any sequence of choices is O(n).
 Step Two:
 Divide p by f,
 Check that the remainder is 0.
 Accept if so.
 The time taken is O(n2) on a multi tape TM.

26. Nondeterministic Primality
Tests26
 Recognizing the primes with a NTM is harder.
While we were able to guess a reason (a
factor) that a number is not a prime, and then
check that our guess is correct, how do we
“guess” a reason a number is a prime? The
nondeterministic polynomial-time algorithm is
based on the fact (asserted but not proved)
that if p is a prime, then there is a number x
between 1 and p – 1 that has degree p - 1

27. Nondeterministic Primality
Tests27
 While we could guess a number x easily, using
the nondeterministic capability of a NTM, it is
not immediately obvious how one then checks
that x has degree p-1.
 The reason is that if we apply the definition of
degree directly, we need to check that none of
x2,x3,... ,xp-2 are 1.
 To do so requires that we perform p - 3
multiplications, and that requires time at least
2n, if p is an n-bit number.

28. Nondeterministic Primality
Tests28
 A better strategy is to make use of another fact that we assert
but do not prove:
 the degree of x modulo a prime p is a divisor of p - 1.
 Thus, if we knew the prime factors of p - 1, it would be sufficient
to check that x(p-1)/q =1 for each prime factor q of p - 1.
 If none of these powers of x is equal to 1, then the degree of
x must be p-1 .
 The number of these tests is O(n).
 Of course we cannot factor p - 1 into primes easily.
 However, non-deterministically we can guess the prime
factors of p - 1, and:
 a) Check that their product is indeed p -1.
 b) Check that each is a prime, using the nondeterministic,
polynomial-time algorithm that we have been designing,
recursively.

29. Nondeterministic Primality
Tests29
 Theorem: The set of primes is in NP.
 PROOF: Given a number p of n-bits, we do the
following.
 First, if n is no more than 2 (i.e., p is 1, 2, or 3),
directly; 2 and 3 are primes, while 1 is not. Otherwise:
1. Guess a list of factors (q1, q2,… , qk), whose binary
representations total at most 2n bits, and none of
which has more than n - 1 bits. It is permitted for the
same prime to appear several times, since p-1 may
have a factor that is a prime raised to a power
greater than 1;
e.g. p = 13 > p - 1 = 12 > factors list is (2, 2, 3).
This part is nondeterministic, but each branch takes
O(n) time.

30. Nondeterministic Primality
Tests30
2. Multiply the q’s together, and verify that their product is p-1.
This part takes no more than O(n2) time and is
deterministic.
3. If their product is p - 1, recursively verify that each is a
prime, using the algorithm being described here.
4. If the q’s are all prime, guess a value of x and check that
x(p1-1)/qj≠1 for any of the qj’s. This test assures that x has
degree p - 1 modulo p, since if it did not, then its degree
would have to divide at least one (p-1)/qj, and we just
verified that it did not.
Note in justification that any x, raised to any power of its
degree, must be 1.
Thus, there are at most k exponentiations, which is surely
no more than n exponentiations, and each one can be
performed in O(n3) time, giving us a total time of O(n4) for
this step.

31. Nondeterministic Primality
Tests31

32. Nondeterministic Primality
Tests32
 Product of the children of any node is less than
the value of the node itself.
 The work required at a node with value i,
exclusive of work done in recursive calls, is at
most a(log2 i)4 for some constant a;
 Thus, The work required by any one level, we
is the maximize of the sum ∑j a (log2(ij))4,
 subject to the constraint that the product i1i2…
is at most p. Because the fourth power is
convex,

33. Nondeterministic Primality
Tests33
 the maximum occurs when all of the value is in
one of the ij’s . If i1=p, and there are no other ij’s,
then the sum is a(log2p)4.
 That is at most an4, since n is the number of bits
in p, and therefore log2p is at most n.
 Our conclusion is that the work required at each
depth is at most O(n4). Since there are at most n
levels, O(n5) work suffices in any branch of the
nondeterministic test for whether p is prime.
 Now we know that both the primes and their
complement are in NP.

34. THANKS FOR YOUR
PATIENCE
34

35. Reference
35
 Agrawal, Manindra. "PRIMES is in P Manindra Agrawal, Neeraj Kayal and
Nitin Saxena* Department of Computer Science & Engineering Indian
Institute of Technology Kanpur Kanpur-208016, INDIA." (2002).
 Homer, Steven, and Alan L. Selman. Computability and complexity theory.
Springer Science & Business Media, 2011.
 Hopcroft, John E., Rajeev Motwani, and Jeffrey D. Ullman. "Introduction to
automata theory, languages, and computation." ACM SIGACT News 32, no.
1 (2001): 60-65.
 Kozen, Dexter. Theory of computation. Springer Science & Business
Media, 2006.
 Lenstra Jr, Hendrik W., and Carl Pomerance. "Primality testing with
Gaussian periods." Lecture Notes in Computer Science (2002): 1-1
 Lewis, Harry R., and Christos H. Papadimitriou. Elements of the Theory of
Computation. Prentice Hall PTR, 1997.
 Xavier, SP Eugene. Theory Of Automata, Formal Languages And
Computation (As Per Uptu Syllabus). New Age International, 2005.

36. Known Problems with Primes
 1. Density
 How many primes are in {1…n}?
 2. Generation
 List all the primes in {1…n}.
 3. Testing
 Given a positive integer n, is n prime?
 4. Random choice
 Pick a random prime number in {1...n}.

37. Sieve of Eratosthenes
37