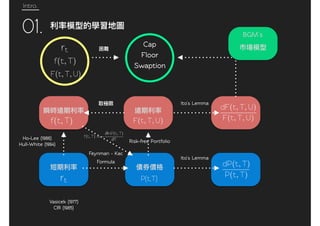
This document discusses the LIBOR Market Model (LMM) for pricing interest rate derivatives. It covers: 1. The HJM framework and finite number of time periods with lognormal LIBOR rates. This is the Brace-Gatarek-Musiela (BGM) model which is also known as the LMM or LFM. 2. Assumptions of the BGM model including positive, continuous LIBOR rates that follow a lognormal process. 3. Pricing of interest rate derivatives like caplets, floorlets, caps and floors using the Black formula under the risk-neutral measure. Caplets and floorlets are priced individually and then summed to obtain prices for caps

1. LIBOR Market Model
From Zero 3o Hero
# - | @Stephan_Chang | tcmail0111@gmail.com

2. Intro.
01.

3. Intro.
01.
Feynman - Kac
Formula
I0o’s Lemma
Ho-Lee (1986)
Hull-Whi0e (1994)
Vasicek (1977)
CIR (1985)
P(t,T)rt
dP(t, T)
P(t, T)
I0o’s Lemma
Risk-free Portfolio
dF(t, T, U)
F(t, T, U)
Cap
Floor
Swaption
F(t, T, U)f(t, T)
rt
f(t, T)
F(t, T, U)
f(t, T) =
lnP(t, T)
T
BGM’s

4. BGM’s LIBOR Ra(e, Swap ra(e
Caplet
Floorlet Swaption
Intro.
01.
# Mer(on (1970)
# Vasicek (1977)
# CIR (1985)
# Ho-Lee (1986)
# Hull-Whi(e (1990, 1994)
# Black-Derman-Toy (1994)
# Ho-Lee ex(ension (1986)
# Hull-Whi(e ex(ension (1990)
# Health Jarrow & Mor(on (1991)

5. BGM’s LIBOR Ra(e, Swap ra(e
Caplet
Floorlet Swaption
Intro.
01.
1973 1995 Black & Scholes Formula
Black & Scholes Formula
Cap Floor Swaption BS-Like
1
2

6. Intro.
01.
3
Payoff
Payoff
C(T) = max(ST K, 0)
P(T) = max(K ST, 0)
T
Payoff
Payoff
Capletk = max(Lk(t) K, 0)
Floorletk = max(K Lk(t), 0)
k

7. Model
02.

8. Model
02.
B A
A B $1 A
P(t, T1)
P(t, T1)-
$1 [1 + (T2 T1)L(t, T1, T2)]
t T1 T2
$1 $1 [1 + (T2 T1)L(t, T1, T2)]
1 + (T2 T1)L(t, T1, T2)
[1 + (T2 T1)L(t, T1, T2)]P(t, T2)+
+
$1- [1 + (T2 T1)L(t, T1, T2)]
LIBOR Forward Ra0e
P(t, T2)

9. Model
02. LIBOR Forward Ra0e
P(t, T1) = P(t, T2)[1 + (T2 T1)L(t, T1, T2)]
P(t, T2)L(t, T1, T) =
P(t, T1) P(t, T2)
(T1, T2)
1 + (T2 T1)L(t, T1, T) =
P(t, T1)
P(t, T2)
1 + x LIBOR Ra0e =[ ]= exp[
T2
T1
r(t, u)du]
HJM f

10. Model
02.
N(d1) S KN(d2)[ ]C = SN(d1) Ke rt
N(d2)
Portfolio
+
1
(T1, T2) P(t, T1)
1
(T1, T2) P(t, T2)
Price of tradable Asset
P(t, T2)L(t, T1, T2) =
P(t, T1) P(t, T2)
(T1, T2)
LIBOR Forward Ra0e

11. Model
02.
= E(Xn|Xn 1) = g(Xn 1)
= E(Xn|Xn 1, Xn 2, ..., X1)
E(Xn|Fn 1)
&
E(Xn|Fn 1) = Xn 1
Spot
Forward
Other Risk-Adjus0ed
measure
measure
measure
QT
Q
Qs
[ ]Bt
P(t, T)
S

12. Model
02.
1
P(t, T2)
P(t, T1) P(t, T2)
(T1, T2) QT2
P(t, T2)L(t, T1, T2)
P(t, T2) QT2
P(t, T2)L(t, T1, T2) =
P(t, T1) P(t, T2)
(T1, T2)
LIBOR Ra0e
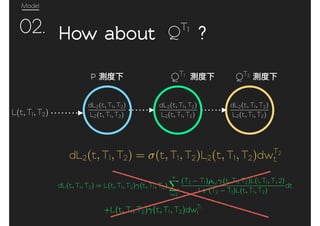
dL2(t, T1, T2) = (t, T1, T2)L2(t, T1, T2)dwT2
t
dLk(t, Tk 1, Tk) = (t, Tk 1, Tk)Lk(t, Tk 1, Tk)dwk
t( )
[ ]
LIBOR Forward Ra0e

13. Intro.
02.
L(t, T1, T2)
QT2
dL2(t, T1, T2)
L2(t, T1, T2)
L(t, T1, T2) = µL(t, T1, T2)dt + L(t, T1, T2) (t, T1, T2)dwt
µL =
L(t, T1, T2)
T1
+ L(t, T1, T2) (t, T1, T2) (t, T1, T2) +
(T2 T1)L2
(t, T1, T2)
1 + (T2 T1)L(t, T1, T2) (t, T1, T2)
| (t, T1, T2)|2
dL2(t, T1, T2) = (t, T1, T2)L2(t, T1, T2)dwT2
t
Martingale Condition
P
dL2(t, T1, T2)
L2(t, T1, T2)

14. Model
02.
P
L(t, T1, T2)
QT2
dL2(t, T1, T2)
L2(t, T1, T2)
dL2(t, T1, T2) = (t, T1, T2)L2(t, T1, T2)dwT2
t
QT1
How about QT1
dL2(t, T1, T2)
L2(t, T1, T2)
dL2(t, T1, T2)
L2(t, T1, T2)
dL(t, T1, T2) = L(t, T1, T2) (t, T1, T2)
k
i=2
(T2 T1) k,i i(t, T1, T2)L(i, T1, T, 2)
1 + (T2 T1)L(t, T1, T2)
dt
+L(t, T1, T2) (t, T1, T2)dwT1
1
?

15. Model
02. BGM’s contribution (1994 - 1997)
1 Rocks SucksQT1
QT2
2
-
-
-

16. Pricing
03.

17. Pricing
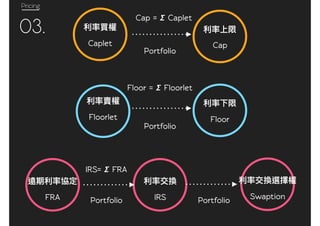
03.
Model for LIBOR (London In0er-Bank Offer Ra0e)
-HJM framework
-Fini0e number, N of time periods
-LIBOR over each period lognormal
- Black’s Formula for caplets satisfied.
BGM model = LMM = LFM
Brace Ga0arek Musiela (1997)
Assumption
- L > 0
- L continuous time
- L follows a lognormal process with de0erministic vol.
Thus, dL(t, Tk 1, Tk) = k(t, Tk 1, Tk)dwk
t
t [0, Ti], i = 1, ...N wk
t : is brownian motion under Qk

18. Pricing
03.
Caplet
Floorlet
Cap
Floor
Portfolio
Portfolio
Cap = 𝞢 Caplet
Floor = 𝞢 Floorlet
FRA IRS SwaptionPortfolio Portfolio
IRS= 𝞢 FRA

19. Pricing
03.
Caplet
Cpl(t, T1, T2, N, K) = N P(t, T2) (T1, T2)Blackc(K, L(t, T1, T2), )
=
T1
t
2(u, T1, T2)du Blackc(K, F, ) = F (
ln(F/K) + 2
) K (
ln(F/K) 2
)
pf:
Cpl = N P(t, T2) (T1, T2) EQ
[
e
T2
t
rudu
P(t, T2)
(L(t, T1, T2) K)+
|Ft]
N P(t, T2) (T1, T2) EQT2
[(L(t, T1, T2) K)+
|Ft]=
MartigaleQT2
dQT2
dQ

20. Pricing
03.
EQT2
[(L(t, T1, T2) K)I{L(t,T1,T2)>K}|Ft]
1 2
2 EQT2
[I{L(t,T1,T2)>K}|Ft] = PrT2
(L(t, T1, T2) > K|Ft)
= EQT2
[L(t, T1, T2)I{L(t,T1,T2)>K}|Ft] KEQT2
[I{L(t,T1,T2)>K}|Ft]
= PrT2
(lnL(t, T1, T2) > lnK|Ft)
= PrT2
(z < d2,k) = (d2,k)
= ...

21. Pricing
03.
1 EQT2
[L(t, T1, T2)I{L(t,T1,T2)>K}|Ft]
= EQT2
[L2(t)e
1
2
T1
t
2
T2
(u)du+ T1
t T2
(u)dwT2 (u))
I{L(t,T1,T2)>K}|Ft]
dwR
(t) = dwT2
(t) T2 (t)dt
= L2(t, T1, T2)ER
[I{L(t,T1,T2)>K}|Ft]
= L2(t, T1, T2)PrR
(L(t, T1, T2) > K|Ft)
= L2(t, T1, T2)PrR
(lnL(t, T1, T2) > lnK|Ft)
= L2(t, T1, T2) (d1, k)

22. Pricing
03.
EQT2
[(L(t, T1, T2) K)I{L(t,T1,T2)>K}|Ft]
= EQT2
[L(t, T1, T2)I{L(t,T1,T2)>K}|Ft]
1 2
KEQT2
[I{L(t,T1,T2)>K}|Ft]
21= +
= L2(t, T1, T2) (d1,k) K (d2,k)

23. Pricing
03.
Cap
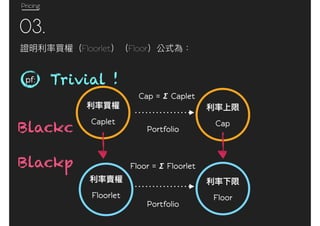
pf: Trivial ! Caplet Cap
Portfolio
Cap = 𝞢 Caplet
Cap(t, T, N, K) =
i= +1
N P(t, Ti)EQ
[
e
Ti
t
rudu
P(t, Ti 1)
(Ti 1, Ti)(L(t, Ti 1, Ti) K)+
|Ft]
= N
i= +1
P(t, Ti) (Ti 1, Ti)Blackc(K, L(t, T1, T2),
Ti 1
t
2
i (u)du)

24. Pricing
03.
Floorlet Floor
Caplet
Floorlet
Cap
Floor
Portfolio
Portfolio
Cap = 𝞢 Caplet
Floor = 𝞢 Floorlet
Blackc
Blackp
pf: Trivial !