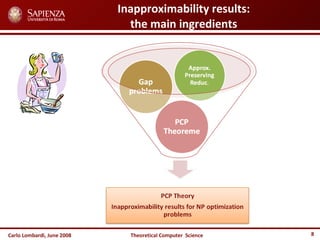
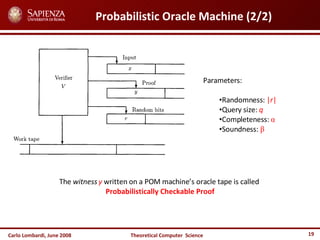
The document discusses inapproximability theory for NP optimization problems. It provides an overview of approximation ratios and approximation-preserving reductions. The key ingredients for obtaining inapproximability results are approximation-preserving reductions, gap problems, and the probabilistic checking proof (PCP) theorem. The PCP theorem shows that any language in NP can be reduced to approximating a gap problem for MAX-3SAT, allowing efficient computation of gap problems and derivation of inapproximability results.

1. Carlo Lombardi, June 2008 Theoretical Computer Science Hardness of Approximation A brief survey of Inapproximability theory for NP optimization problems

2. Carlo Lombardi, June 2008 Theoretical Computer Science Overview Optimization problem: Definition NP Optimization Approximability and Inapproximability Approximation-Preserving Reduction Gap Problems, Karp reduction, PCP Theorem Probabilistic Verification

3. Carlo Lombardi, June 2008 Theoretical Computer Science Optimization problem “ find the best solution from all feasible solution” x = instance of input y = “ witness ” solution D(x) = set of all feasible solution F(x,y) = real-valued function wich assigns a “ score ” to y If both y belongs to D(X) F(x,y) are polynomial time computable then OPT(x) belongs to NPO class

4. Carlo Lombardi, June 2008 Theoretical Computer Science Approximation ratio Consider a map: This map is said to approximate OPT(x) within a factor r(x)>=1 if: The best such r(x) is said approximation ratio If A is p-time computable we say that OPT(x) is approximable within a factor of r(x) If there are no A p-time computable under some complexity theoretic hipothesis then r(x) is said inapproximability ratio OPT(x) <= r(x) F(x,A(x)) if OPT(x) is a MAX-P F(x,A(x)) <= r(x) OPT(x) if OPT(x) is a MIN-P

5. Carlo Lombardi, June 2008 Theoretical Computer Science Example: Set Cover Problem Let be: x : a polynomial size set system S y : subsystem S1 S iff Find s.t. is minimized Feige has shown that that the set cover cannot be approximate within a factor of is the approximation boundary for Set Cover Problem but unfortunately…this is only an inapproximability result for a specific problem …not a more general theory…

6. Carlo Lombardi, June 2008 Theoretical Computer Science Question In which way we can obtain inapproximability results for optimization problems? Roughly speaking, how we can find a lower bound for approximation ratio of optimization problems?

7. Carlo Lombardi, June 2008 Theoretical Computer Science Timeline for a more general inapproximability theory 1972 – Graham : exact bounds on the performance of various bin packing heuristics 1974 – Jhonson : Subest Sum, Set Cover, MAX k-SAT bounds 1976 – Shani & Gonzalez : TSP problem bound Garey & Jhonson : Gap amplification technique for Chromatic Number of a graph bound 1991 – Feige : MIP for MIN-Clique bound Papadimitriou & Yannakakis :Using L reduction (app-reserving) 1992 – Arora et al.: Using PCPs for MAX-3SAT Problem bound “ EUREKA!!!”

8. Carlo Lombardi, June 2008 Theoretical Computer Science Inapproximability results: the main ingredients

9. Carlo Lombardi, June 2008 Theoretical Computer Science Approximation-Preserving Reduction (1/2) If A Cook reduces to B we can state that “ the hardness of B follows from the hardness of A” but we CANNOT state that “ if A is hard to approximate then B is hard to approximate” To ensure reducing hardness of approximation we need a new definition of reduction…

10. Carlo Lombardi, June 2008 Theoretical Computer Science Approximation-Preserving Reduction (2/2) Let be: F 1 (x,y) and F 2 (x ’,y ’) to be optimized for y and y ‘ OPT 1 (x) and OPT 2 (x ‘) the corresponding optimum a KARP-LEVIN reduction involves two polynomial- time maps f and g s.t.: (Instance transformation) (Witness transformation) Let be: opt 1 = OPT 1 (x) opt 2 = OPT 2 ( f (x)) appr 1 = F 1 (x,g(f(x),y ’)) appr 1 = F 2 (f(x),y ‘) An approximation-preserving reduction scheme is a relation between this four entities that express the following: “ If appr 2 well approximate opt 2 then appr 1 well approximate opt 1 “

11. Carlo Lombardi, June 2008 Theoretical Computer Science Gap Problem Let be : OPT : a maximizationproblem T l (x) : a lower bound for OPT T u (x) : an upper bound for OPT Both T l (x) and T u (x) are p-time computable in x If we can efficiently approximate OPT(x) within a factor better than r(x)= T u (x) / T l (x) then we can solve with only additive polynomial time also the so called GAP PROBLEM : 1 if OPT(x) >= T u (x) Gap( OPT , T l , T u ) 0 if OPT(x) <= T l (x) ANY if T l (x) < OPT(x) < T u (x) If OPT is a minimization problem the roles of 0 and 1 in the above definition get exchanged

12. Carlo Lombardi, June 2008 Theoretical Computer Science From languages to gap problem We can use Karp reduction to map a language into a Gap Problem A such reduction is a polynomial time computable map f from to input instances of OPT (max-problem) s.t. Y N T u ( f (x)) T l ( f (x))

13. Carlo Lombardi, June 2008 Theoretical Computer Science PCP Theorem Given an and a language there exists a polynomial-time computable function such that: if then f (x) is a formula in which all disjunctions are simultaneously satisfable if then f (x) is a formula in which one can satisfy at most 1- ε fraction of all clauses Considering we are discussing about optimization problem we can restate the Theorem: Any language in NP is Karp reducible to Gap(Max-3SAT, 1- ε , 1) where Max-3SAT( φ )= max y F( φ ,y) being φ a 3CNF

14. Carlo Lombardi, June 2008 Theoretical Computer Science Karp reduction & gap problem Karp reduction are approximation-preserving reduction We can reduce a gap problem G to a gap problem G’ preserving approximation results Consider two maximization problem OPT 1 and OPT 2 with bounds respectively T l , T u , T’ l , T’ u and A function f p-time computable from input instances of OPT 1 to input instances of OPT2 s.t.: if OPT 1 (x) <= T l (x) then OPT(f(x)) <= T l (f(x)) if OPT 1 (x) >= T u (x) then OPT(f(x)) >= T u (f(x)) f is a Karp reduction from Gap( OPT 1 , T l , T l ) to Gap( OPT 2 , T’ l , T’ l ) Gap( OPT 1 , T l , T u ) is NP-Hard Gap( OPT 2 , T’ u , T’ u ) is NP-Hard

15. Carlo Lombardi, June 2008 Theoretical Computer Science The main philosophy of PCP Theory

16. Carlo Lombardi, June 2008 Theoretical Computer Science Question How it’s possible to compute efficiently gap problems?

17. Carlo Lombardi, June 2008 Theoretical Computer Science Probabilistic Proof System A proof system consists of a verifier V and a prover P Given a stastement x , such as “ φ is satisfable” P produces a candidate proof y for the statement φ V read the pair ( φ ,y ) and either accepts or reject the proof y for φ Any proof system have two property: COMPLETENESS : if x is true  exists y s.t. V(x,y) accepts SOUNDNESS : if x is false  for every y V(x,y) rejects A language L is in NP if there is a deterministic polynomial time verifier V and a polynomial p s.t.:

18. Carlo Lombardi, June 2008 Theoretical Computer Science Probabilistic Oracle Machine (1/2) What’s happen if we allow V to be randomized? Let be: M y a probabilistic RAM with oracle y and random string r M is said to accept a language L with completness α and soudness β (1>= α > β >0) iff if then ther is a y s.t. Probr(My(x,r)=1)>= α if then for every y it holds that Probr(My(x,r)=1)<= β

19. Carlo Lombardi, June 2008 Theoretical Computer Science Parameters: Randomness: | r | Query size: q Completeness: α Soundness: β Probabilistic Oracle Machine (2/2) The witness y written on a POM machine’s oracle tape is called Probabilistically Checkable Proof

20. Carlo Lombardi, June 2008 Theoretical Computer Science Connection between POM and OPT problem L Karp reduces to Gap(OPTM, β , α ) If L is NP-Hard , approximating OPT M within a factor better than α / β is also NP-Hard