The document presents a model for optimal tracking of leveraged and inverse ETFs, focusing on the trade-off between tracking error and excess return while considering trading costs. It discusses the effects of compounding on performance, underexposure issues, and optimal rebalancing strategies, along with robust findings that maintain independence from volatility dynamics. Key results highlight that performance can be evaluated through the product of excess return and tracking error, offering insights into fund comparisons.










![Background Main Result Heuristics Conclusion
Main Result
Theorem (Exact)
Assume Λ = 0, 1.
i) For any γ > 0 there exists ε0 > 0 such that for all ε < ε0, the system
1
2 ζ2
W (ζ) + ζW (ζ) − γ
(1+ζ)2 Λ − ζ
1+ζ = 0,
W(ζ−) = 0, W (ζ−) = 0,
W(ζ+) = ε
(1+ζ+)(1+(1−ε)ζ+) , W (ζ+) = ε(ε−2(1−ε)ζ+−2)
(1+ζ+)2(1+(1−ε)ζ+)2
has a unique solution (W, ζ−, ζ+) for which ζ− < ζ+.
ii) The optimal policy is to buy at π− := ζ−/(1 + ζ−) and sell at
π+ := ζ+/(1 + ζ+) to keep πt = ζt /(1 + ζt ) within the interval [π−, π+].
iii) The maximum performance is
lim sup
T→∞
DT −
γ
2
D T = −
γσ2
2
(π− − Λ)2
,](https://image.slidesharecdn.com/etfsmichigan-160615151047/85/Leveraged-ETFs-Performance-Evaluation-11-320.jpg)





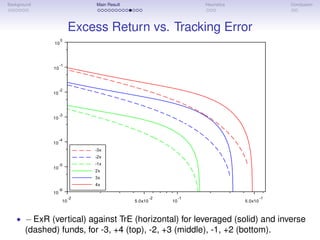

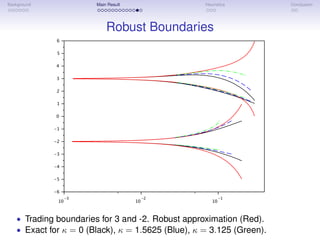



![Background Main Result Heuristics Conclusion
Identifying System
• Above inequalities become
0 ≤ W(ζ) ≤
ε
(1 + ζ)(1 + (1 − ε)ζ)
,
γΛ
ζ
1 + ζ
−
γ
2
ζ2
(1 + ζ)2
− λ −
1
2
ζ2
W (ζ) ≤ 0,
• Optimality conditions
1
2
ζ2
W (ζ) − γΛ
ζ
1 + ζ
+
γ
2
ζ2
(1 + ζ)2
+ λ =0 for ζ ∈ [ζ−, ζ+],
W(ζ−) =0,
W(ζ+) =
ε
(ζ+ + 1)(1 + (1 − ε)ζ+)
,
• Boundaries identified by the smooth-pasting conditions
W (ζ−) =0,
W (ζ+) =
ε(ε − 2(1 − ε)ζ+ − 2)
(1 + ζ+)2(1 + (1 − ε)ζ+)2
.
• Four unknowns and four equations.](https://image.slidesharecdn.com/etfsmichigan-160615151047/85/Leveraged-ETFs-Performance-Evaluation-23-320.jpg)

