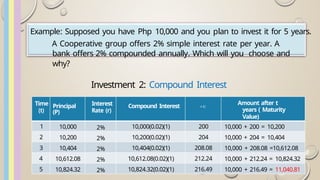
The document discusses the management of hard-earned money, focusing on concepts of simple and compound interest. It provides definitions and examples of calculating interest, maturity value, and present value while illustrating the benefits and drawbacks of both simple and compound interest over time. Additionally, it covers annuities, their types, and calculations for future and present values related to regular payments.

2. "What are the ways in handling hard
– earned money like the salary of
your parents or your own salary if you
are working. "

3. OBJECTIVES
www.gen_math.com
Illustrates simple and compound interests;
Distinguishes between simple and compound interests;
Computes interest, maturity value(future value)
and present value in simple interest; and
Solves problems involving simple interest.

4. Principal
Lender or Creditor
Rate
Maturity Value or Future
Value
Borrower or
Debtor Time or
Term
Compound Interest
Repayment date or Maturity
date
Origin or Loan date
Simple Interest
Interest
Lender or creditor person or institution who invests the money or makes the funds available.
Borrower or debtor person or institution who owes the money or avails of the funds from the lender.
Origin or loan date date on which the money is received by the borrower.
Maturity value or future value
(F)
amount after t years that the lender receives from the borrower on the maturity
date.
Time or term (t)
the amount of time in years the money is borrowed or invested, length of
time between the origin and maturity dates.
Principal (p)
the original amount of money invested or borrowed.
– also known as the capital

5. Rate (r)
annual rate, usually in percent, charged by the lender, or rate of
increase of the investment.
Interest (I) amount earned or paid for the use of money.
Simple Interest (Is) interest computed on the principal amount of loan or money invested.
Compound Interest (Ic) interest is computed on the principal amount and also on the accumulated
past interests.
Repayment date or maturity date date on which the money borrowed or loan is to be completely repaid.

6. OBJECTIVES LESSONS
www.gen_math.com
SIMPLE
INTERES
T
COMPOUN
D
INTEREST
V

7. Example: Supposed you have Php 10,000 and you plan to invest it
for 5 years. A Cooperative group offers 2% simple interest rate
per year. A bank offers 2% compounded annually. Which will you
choose and why?

8. Example: Supposed you have Php 10,000 and you plan to invest it for 5 years.
A Cooperative group offers 2% simple interest rate per year. A
bank offers 2% compounded annually. Which will you choose and
why?
Investment 1: Simple Interest
Time
(t) Principal (P)
Interest
Rate (r) Simple Interest ,s
Amount after t
years ( Maturity
Value)
1 10,000 2% 10,000(0.02)(1) 200 10,000 + 200 = 10,200
2 10,000 2% 10,000(0.02)(2) 400 10,000 + 400 = 10,400
3 10,000 2% 10,000(0.02)(3) 600 10,000 + 600 = 10,600
4 10,000 2% 10,000(0.02)(4) 800 10,000 + 800 = 10,800
5 10,000 2% 10,000(0.02)(5) 1,000 10,000 + 1,000 = 11,000

10. Example: Supposed you have Php 10,000 and you plan to invest it for 5 years.
A Cooperative group offers 2% simple interest rate per year. A
bank offers 2% compounded annually. Which will you choose and
why?
Investment 2: Compound Interest
Time
(t)
Principal
(P)
Interest
Rate (r)
Compound Interest ,c
Amount after t
years ( Maturity
Value)
1 10,000 2% 10,000(0.02)(1) 200 10,000 + 200 = 10,200
2 10,200 2% 10,200(0.02)(1) 204 10,000 + 204 = 10,404
3 10,404 2% 10,404(0.02)(1) 208.08 10,000 + 208.08 =10,612.08
4 10,612.08 2% 10,612.08(0.02)(1) 212.24 10,000 + 212.24 = 10,824.32
5 10,824.32 2% 10,824.32(0.02)(1) 216.49 10,000 + 216.49 = 11,040.81

12. Simple interest remains constant throughout the investment term.
In compound interest, the interest from the previous year also
earns interest. Thus, the interest grows every year.

13. Simple Interest (Is)
Compound Interest (Ic)
Given: P = Php 5,000 r= 5% = 0.05 t = 3yrs.
P = 5,250 P = 5,500 P = 5,750
Timeline 0 1 2 3
P = 5,000 P = 5,000 P = 5,000
I = 250 I = 250 I = 250
P = 5,250 P = 5,512.50 P = 5,788.13
Timeline 0 1 2 3
P = 5,000 P = 5,250 P = 5,512.50
I = 250 I = 262.50 I = 275.63

14. OBJECTIVES LESSONS
www.gen_math.com
Computes interest, maturity
value(future value) and
present value in simple
interest
Solves problems involving
simple interest.

15. P r t P r
Prt
=Pt
r
IS
Magic Triangle for Simple Interest
P
=
IS
P r t

16. IS IS
IS
r t

17. Maturity Value or (Future Value or Amount or
Balance)
or or
Where: IS = simple interest
P = principal
r = rate of interest or simply rate
t = time in year
F = future value or maturity value

18. Example 1: When Lianne bought a new laptop for her work, she
borrowed
Php 30,000 at a rate of 15% for 9 months. How much interest will
she
pay?
t = 9 months =
I = Prt
I = (30,000)(0.15)(
)
r = 15% = 0.15
P = 30,000
Given: I = ?

19. Example 2: To buy the school supplies for the coming school year, you get
a
summer job at a resort. Supposed you have Php4,200 of your salary and
deposit
it into an account that earns simple interest. After 6 months, the balance is
Php4,240. What is the annual interest rate?
I = 4,240 - 4,200 = 40
r =
40
r =
40
t = 6 months =
P = 4,200
r =
Given:
(4,200)
r = ?

20. 2, 100
T = 0.019 or 1.9%

21. Example 3: If Php10,000 is invested at 4.5% simple interest, how long will it
take to
grow to Php 11,800
I = 11,800 – 10,000 = 1,800
r = 4.5% = 0.045
1,800
(10,000)
(0.045)
=
1,800
450 t = 4 y
ears
P = 10,000
t =
t = ?

22. Example 4: A loan institution charges 12% simple interest for 3 –year, Php
60,000 loan.
a. Find the total interest of the loan.
b. Find the total amount that must be paid to the loan institution at
the end of 3 years.
r = 12% = 0.12
' = Prt
' = (60,000) (0.12) (3)
' =pℎp 21,600
F = P + I
F = 60,000 + 21,600
F= pℎp 81, 600
P = 60,000 t = 3 years
I = ?

23. Example 5: Find the maturity value of a loan amounting to Php50,000 at
9%
for 2 years .
r = 9% = 0.09
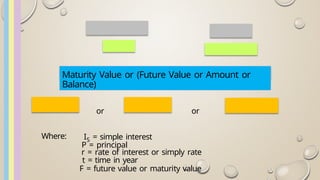
F = P(1 + rt ) or A = P + I
= 50,000[1 +( 0.09 )(2)]
= 50,000( 1. 18)
F = Php 59,000
t = 2 years
P = 50,000
F = ?

24. Example 6: Find the present value of Php86,000 at 8% for 3 years .
P = ?
P =
F
1 +
Tt
r = 8% = 0.08
=
86,000
[1 + 0.08
3 ]
=
86,000 86,000
= = Php
69,354.84
t = 3 years
F = 86,000
[1 + 0.24 ]

25. Evaluate you
r
learnings
Complete the table
Principal (P) Rate (r) Time (t) Interest (I)
1. P 2.5% 3 years Php500
Php 5,000 2. r
7yrs.and 3
months
Php 6,000
Php 12,000 0.03% 3. t Php350
Php 18,000 10% 15 years 4. I

27. COMPOUND INTEREST
Lesson 2
ROMADEL R. PERALTA
Subject Teacher

28. 1. What is simple interest? On what real - life
situation
does interest occur?
2. How do you find the interest and
maturity value of an amount earning
simple interest?

29. 3. What formula can you make as you
generalize simple interest? Maturity
(future) value?

30. • compute interest, maturity value , and
present
value in compound interest,
• solve problems involving compound
interest,

31. • actively participate in virtual discussion.

32. COMPOUND INTEREST
(or Compounding Interest)
IS THE INTEREST ON A LOAN OR DEPOSIT
CALCULATED
BASED ON BOTH THE INITIAL PRINCIPAL AND THE
ACCUMULATED INTEREST FROM PREVIOUS PERIODS.

33. Definition of Terms
Frequency of conversion (m) – the number of conversion
periods in one(1) year.
Interest period (t) – time between successive conversion of
interest.
Total number of conversion period (n)
n = (frequency of conversion )(time in year)
n = mt
Nominal rate(r) – annual interest rate.

34. Conversion Period
annually (once a year):
semi-annually(every 6 months):
quarterly(every 3 months):
monthly(every month):

35. Example 1: Nominal rate and the corresponding frequencies
of conversion and interest rate for each period
Nominal rate (r)
Frequency
of
conversion
(m)
Conversion
period
Interest rate per conversion
period
(i)
2% compounded annually
r = 0.02
2% compounded semi- annually
r = 0.02
2% compounded quarterly
m = 2 6 months
r = 0.02
2% compounded monthly
m = 4 3 months
r = 0.02
2%
m = 12 1 month
m = 365
r =
1
m=
compounded
1ye

36. Maturity Value
where
F = maturity or future value at the end of the term
P = principal or present value
r = nominal rate
t = term/time in years
m= frequency of conversion

37. MATURITY VALUE & COMPOUND INTEREST
Example 2: Find the maturity value and interest if Php15,000 is
deposited in the bank at 2% compounded quarterly in 5 years.
Given: P = Php15,000 r = 2% = 0.02 t = 5 years m = 4
Find: a. maturity value(F)

38. Example 3: Find the maturity value and interest if Php15,000 is deposited
in the bank at 2% compounded semi-annually in 5 years.
(round answers into 2 decimal places if needed).
Given: P = Php15,000 r = 2% = 0.02 t = 5 years m = 2
Find: a. maturity value(F)
MATURITY VALUE & COMPOUND INTEREST

39. Example 4: Christine borrowed Php50,000 and promise to pay the principal
and interest at 12% compounded monthly. How much must she
repay after 6 years.(round answers into 2 decimal places if needed).
Given: P = Php50,000 r = 12% = 0.12 t = 6 years m = 12
Find: maturity value(F)
MATURITY VALUE

40. where
F = maturity or future value at the end of the term
P = principal or present value
r = nominal rate
t = term/time in years
m= frequency of conversion
PRESENT VALUE(P) AT COMPOUND
INTEREST

41. PRESENT VALUE and COMPOUND INTEREST
Example 5: Find the present value ofPhp50,000 due in 4 years if money is
invested at 15% compounded semi - annually.
(round answers into 2 decimal places if needed).
Given: F = Php50,000 r = 15% = 0.15 t = 4 m = 2
Find: Present value(P)

42. PRESENT VALUE and COMPOUND INTEREST
Example 6: What is the present value of Php25,000 due in 2 years and 6
months at 10% compounded quarterly.
(round answers into 2 decimal places if needed).
Given: F = Php25,000 r = 10%
Find: Present value(P)
= 0.10 m = 4

43. 2: Supposed your father deposited in your bank account
Php10,000 at an annual interest rate of 0.8% compounded yearly when you
cannot withdraw the amount until you finish Grade 12. How much will you h
Solve the following problem:
1. What is the present value of Php50,000 due in 7 years if
interest rate is 10% compounded annually ?

44. General
Mathematics
Lesson 3
SIMPLE AND
GENERAL ANNUITIES
ROMADEL R. PERALTA
Subject Teacher

45. • Actively participate in virtual discussion.
OBJECTIVES
•Illustrates simple and general annuities
• Distinguish simple and general annuities
• Find the future and present values of simple annuities; and

46. What is Annuity?
Annuity is a fixed some of money
paid to someone at regular intervals,
subject to a fixed compound interest
rate.

47. ANNUITIES
According to
payment interval
and interest
period
Simple Annuity - interest
conversion or compounding period
is the same as the payment
interval.
General Annuity - interest
conversion or compounding
period is not the same as
the payment interval
According to time
of payment
Ordinary Annuity or Annuity
Immediate- an annuity in which
the periodic payment is made at
the
end of each payment interval.
Annuity Due - an annuity in
which the periodic payment
is made at the beginning of
each payment interval.
According
to
duration
Annuity Certain - an annuity in
which payments begin and end
at definite time.
Contingent or Annuity
Uncertain - an annuity
payable for an indefinite
duration
dependent on some
certain event.
(ex.insurance)

48. Can you cite an example of an
annuity?
*Rent payment
*Pension
*Monthly payment of carloan or mortgage

49. Definition of Terms
Term of an annuity, (t)
- the time between the first payment interval and last payment interval.
Regular or Periodic payment, (R)
- the amount of each payment.
Future value of an annuity, (F)
- is the total accumulation of the payments and interest earned.
Present value of an annuity, (P)
- is the principal that must be invested today to provide the
regular payment of an annuity.

50. FORMULA
Future Value of Simple
Ordinary Annuity, F
Present Value of Simple
Ordinary Annuity, P
Periodic Payment R of
an annuity.

51. General Annuity
Simple Annuity
Example 1: Determine if the given situation represent simple annuity
or general annuity.
a. Payments are made at the end of each month for a loan
that charges 1.05% interest compounded quarterly.
b. A deposit of Php15,000 was made at the end of every three
months to an account that earns 5.6% interest compounded quarterly.

52. Ordinary Annuity
Annuity due
Example 2: Determine whether the situation describes an ordinary annuity
or an annuity due.
a. Anton’s monthly mortgage payment for his car is Php35,148.05 at the
end of each month.
b. The rent of an apartment is Php 8,000 and due at the beginning of
each month.

53. Example 3: Supposed Mrs. Santos would like to save Php3,000 every month
in afund that gives 9% compounded monthly. How much is
the amount or the future value of her savings after 6 months?.
R = Php3000 r = 9%= 0.09 t = 6months = 0.5 year m= 12
n= mt = (12)(0.5) = 6
Future Value (F)
) = 3000(6.113631347)
F = Php 18,340.89

54. Example 4: In order to save for her highschool graduation, Marie decided to
save Php200 at the end of each month. If the bank pays 0.25%
compounded monthly , how much will her money beat the
end of 6 years?
Given:
Find:
R = Php200
Future Value (F)
r = 0.25%= 0.0025 t = 6 years m= 12
n= mt = (12)(6) = 72
= Php 14,507.02

55. Example 5: Al works very hard because he wants to have enough money on
his retirement account when he reaches the age of 60. He
wants to withdraw Php 36,000 every 3 months for 20 years
starting 3
months after he retires. How much must Al deposit at
retirement if 12% per year compounded quarterly for the
annuity?
R = Php36,000 r = 12%= 0.12 t = 20 years m= 4
n= mt = (4)(20) = 80
Present Value (P)
P = Php 1,087,227.48
Given:
Find:

56. The cash value or cash price of a purchase is equal to the down payment (if there is
any plus the present value of the installment payment. CV= DP + P
DP = Php200,000
Find:
R = Php16,200 r = 10.5%= 0.105 t = 5 years m= 12
n= mt = (12)(5) = 60
Cash Value = Down payment + Present value
P = Php 753,702.20
CV= DP + P
CV= 200,000 + 753,702.20
CV= Php 953,702.20
Present Value
Given:

57. Example 7: Paul borrowed Php100,000, he agrees to pay the principal plus interest
by paying an equal amount of money each year for 3 years. What
should be his annual payment if the interest is 8% compounded
annually?
Given:
P = Php100,000
r = 8% = 0.08
t = 3 years
m= 1
n= mt = (1)(3) = 3
Find: Periodic payment(R)
R = Php38, 803.35

58. Example 8: Mr. Abayawould like to save Php500,000 for his daughter’s college
education. How much should he deposit in a savings account every
6 months for 12 years if interest is 1% compound semi-annually?
Given:
F = Php500,000
r = 1% = 0.01
t = 12 years
m= 2
n= mt = (2)(12) = 24
Find: Periodic payment(R)
R = Php19, 660.31

59. Answer the following as quick as you can.
Regular or Periodic payment
2.A type of an annuity in which
the periodic payment is made
at the end of each payment
interval.
3. Annuity Due - an annuity in which the periodic payment is made at
the beginning of each payment interval
1.It is the amount of each
Ordinary Annuity

60. Answer the following as quick as you can.
• If you pay Php 5,000 at the end of each month for 20 years on account
that pays interest at 6% compounded monthly, how much do you have
after 20 years?
R = Php5,000 r = 6%= 0.06 t = 20 years m= 12
n= mt = (12)(20) = 240
Find:
5000 (462.0408952)= Php 2,310,204.48
=
Given:
Future Value

61. GENERAL MATHEMATICS
GENERAL ANNUITY, AND
DEFERRED ANNUITY
ROMADEL R. PERALTA
SUBJECT TEACHER

62. OBJECTIVES
a. Finds the future and present value of general annuity.
b. Calculates the fair market value of a cash flow stream that
includes an annuity.
c. Calculates the present value and period of deferral of a deferred annuity.
d. Actively participate in the virtual discussion.

63. Examples of General Annuity
DEFINITION OF TERMS
General Annuity – an annuity where the payment interval is not the
same as the interest period.
General Ordinary Annuity – is a general annuity in which the periodic
payment is made at the end of the payment
interval.
1. Monthly installment of a car, lot, or house with an interest rate that is
compounded annually.

64. 2. Paying a debt semi-annually when the interest is compounded monthly

65. F = R
(1+i)n −1
i
n = (m1) (t)
FORMULA
P = R
1− (1+i)−n
i
i = (1 + )m2/m1 − 1

66. where
R is the regular payment
i is the equivalent interest rate per payment interval converted from the

67. Example 1. Alex started to deposit of Php 2,000 monthly in a fund that pays 5% compounded
quarterly .
How much will be in the fund after 10 years.
Given:
R = PℎP 2,000
m1 = 12
m2 = 4
rm2 = 0.05
t = 10
n = m1 t
= 12 10
n = 120
Convert 5% compounded quarterly to
its
equivalent interest rate for monthly
payment interval.
i = (1 + )m2/m1
− 1 i = (1 +
)4/12 − 1
i =
0.004149425119

68. Find the future value
(1 +
0.00419425119)120
− 1 F =
2,000
0.00419425119
0.652447596
F = 2,000
0.00419425119
F = 2,000 (155.5575874)
F = PℎP 311,
115. 18

69. Example 2. A teacher saves Php8,000 for every 6 months in a bank that pays 0.15% compounded
monthly. How much will be her savings after 5 years.
Given:
R = PℎP 8,000
m1 = 2
m2 = 12
t = 5
Tm2 = 0.0015
n = m1 t = 2 5
= 10
Convert 0.15% compounded
monthly to its equivalent interest
rate for each semi-annual
payment interval.
i = (1 + )m2/m1 − 1
i = (1 + )12/2 − 1
i = (1.000125)6
− 1
i = 1.000750234 − 1
i = 0.000750234
Find the future value
F = 8000
F = 8000
0.
0
0
0752771903
000750234
6
F = 8000 (10.03382816)
F = Php 80,270.63

70. Example 3. XYZ Bank pays interest at the rate of 2% compounded quarterly. How much will have
in the
bank at the end of 5 years if the deposit is Php 2,000 every month.
Given:
R = PℎP 2,000
m1 = 12
m2 = 4
t = 5
Tm2 = 0.02
n = m1 t = 12 5
= 60
Convert 2% compounded
quarterly to its equivalent
interest rate for
monthly payment interval.
i = (1 + )m2/m1 − 1
i = (1 + )4/12 − 1
i = 1.001663896 − 1
i = 0.001663896
Find the future value
F = 2000 (1+0.
0
0
01663896
00166389
60
−1
F = 2000
F = 2000 (63.04212403)

71. F = Php 126,084.25

72. PRESENT VALUE

73. P = R
1− (1+i)−n
i
FORMULA
i = (1 + )m2/m1 − 1
where
R is the regular payment
i is the equivalent interest rate per payment interval converted
from the interest rate per period.
n is the number of payments
r is the nominal rate
m1 is the payment interval
m2 is the length of compounding period.
t is the term of annuity
n = (m1)

74. Example 4. Kim borrowed an amount of money from Kate. She agrees to pay the principal plus
interest
by paying Php38, 973.76 each year for 3 years. How much money did she borrow
if interest is 8% compounded quarterly.
Given:
R = PℎP 38,973.76
m1 = 1
m2 = 4
t = 3
Tm2 = 0.08
n = m1 t = 1 3 =
3
Convert 8% compounded
quarterly to its equivalent rate
for each
payment interval.
i = (1 + )m2/m1 − 1
i = (1 + )4/1 − 1
i = 1.08243216 − 1
i = 0.08243216
Find the present value
1− (1+i)−n
i
P = 38,973.76
1− (1
0.082
0824
43
32
2
16
16 )−3
P = 38,973.76 1
−
0
0.
0
7884931
8243216
75
P = 38,973.76
0
0
.
.
211506
082432
8
1
2
6
4
P = 38,973.76 (0.2565828973)
P = R

75. P = Php 100,000

76. Example 5. Mrs. Morales would like to buy a television set payable for 6 months starting at the end
of
the month. How much is the cost of the television set if her monthly payment is
Php3,000 and interest is 9% compounded semi-annually.
Given:
R = PℎP 3,000
m1 = 12
m2 = 2
t = 6montℎs = 0.5
Tm2 = 0.09
n = m1 t = 12 0.5
= 6
Convert 9% compounded semi-
annually to its equivalent rate for
monthly payment interval.
i = (1 +
T
m2
m2 )m2/m1 − 1
i = (1 + )2/12 − 1
i = 1.007363123 − 1
i = 0.007363123
Find the present value
1− (1+i)−n
i
P = 3,000
1− (1
0.0073
00736
63
31 2
1
2
3
3 )−6
P = 3,000
1
−
0
0
0
.
9
0
5
7
693779
363123
9
P = 3,000
0
0.0430622
007363123
P = 3,000 (5.848360922)
P = R

77. P = Php
17,545.08

78. Calculates the Fair Market Value of a Cash Flow Stream that
includes Annuity
1− (1+i)−n P = R
i
Cash flow - a term that refers to payment that can either be inflows
(payments received) or outflows(payments made).
Fair Market Value or economic value- refers to a single amount that is
equivalent to the value of the payment stream at the
date. This particular date is called focal date.
F
(1 +
P

79. Example 1. Mr. Abad received two offers on a house that he wants to sell. Mr. Cruz’s offer is Php
50,000
down payment and a Php1,000,000 lump sum payment 5 years from now. Mr. Solis
has offered Php50,000 plus Php40,000 every quarter for 5 years. Compare the fair
market value of the
two offers if money can earn 5% compounded annually. Which offers has a
higher market value.
DP= Php 50,000
F = Php 1,000,000
r = 5% = 0.05
t = 5
m = 1
i =
T
=
0.05
= 0.05
n = mt = (1)(5) = 5
P =
F
1,000,000
P =
1,000,000 1,000,000
P = 5
=
(1.05)
(1 +
(1 +
m
Mr. Cruz’s

80. P = PℎP 783,526.17
FaiT MaTket Value
FMV = DP + P
FMV = 50,000 + 783,526.
17
FMV = PℎP
833,526.17

81. Example 1. Mr. Abad received two offers on a house that he wants to sell. Mr. Cruz’s offer is Php
50,000
down payment and a Php1,000,000 lump sum payment 5 years from now. Mr. Solis
has offered Php50,000 plus Php40,000 every quarter for 5 years. Compare the fair
market value of the two offers if money can earn 5% compounded annually. Which
offers has a higher market value.
DP= Php 50,000
R = Php 40,000
rm2 = 0.05
t = 5
m1 = 4
m2 = 1
n = mt = (4)(5) = 20
Convert 5% compounded
annually to its equivalent
interest rate for quarterly
payment
interval.
i = (1 + )m2/m1 − 1
i = (1 + )1/4 − 1
i = (1.05)1/4 − 1
i = 0.012272234
Mr. Solis’s offer

82. Find the present value
P = R
P = 40,000
1− (1
+
0
0.0
01
1
2
2
2
2
7
7
2
2
2
2
3
3
4
4)−20
p = php 705, 572. 68
Fair Market alue
Ⅴ
FMV = DP + P
FMV = 50,000 + 705,572.68
FMV = php 755, 572. 68
1− (1+i)
n
−
i

83. Mr. Cruz’s offer Mr. Solis’s offer
Down payment =pℎp 50,000 Down payment =pℎp 50,000
Present Value = pℎp 783,526.17 Present Value= pℎp 705,572.68
Fair Market Value = pℎp 833,526.17 Fair Market Value = pℎp 755,572.68

84. CALCULATES THE PRESENT VALUE AND PERIOD OF DEFERRAL OF A DEFERRED
ANNUITY.
Deferred Annuity - an annuity that does not begin until a given time interval has
passed.
Period of Deferral - time between the purchase of an annuity and the start of the
payments for the deferred annuity.
Annual payments of Php 2,000 for 24 years that will start 12 years from now.
y0 y1 y2 y3 y4 … y11 y12 y13 …
DEFINITION OF

85. 6 periods or 6 months
4 periods or 4 years
Find the period of deferral in each of the following deferred annuity problems.
1. Monthly payments of Php2,000 for 5 years that will start 7 months from now.
2. Annual payment of Php8,000 for 2 years that will start 5 years from now.

86. 7 periods or 7 quarters
9 periods or 9 semi-annual intervals
Find the period of deferral in each of the following deferred annuity problems.
3. Quarterly payments of Php5,000 for 8 years that will start 2 years from
now.
4. Semi – annual payments of Php60,000 for 10 years that will start 5 years from
now.

87. PRESENT VALUE OF A DEFERRED ANNUITY
P = R
1− (1+i)−(k+n)
i
n = mt
- R
i
r
i =
R is the regular payment
i is the interest rate per period
n is the number of payments
k is the number of conversion periods in the deferral
1− (1+i)
m

88. Example 1. On his 40th
birthday, Ms. Flores decided to buy a pension plan for herself. This plan
will allow
her to claim Php10,000 quarterly for 5 years starting 3 months after her 60th
birthday. What one-time payment should she make on his 40th
birthday to pay off
this pension plan, if the
interest rate is 8% compounded quarterly.
Given:
1− (1+i)−(k+n) 1− (1+i)−k
i i
P = 10,000
1− (1+0
.0
0
2
0
(80+20)
- - 10,000
1− (1
+
0
0.
0
0
2
2)−80
P = 10,000 43.09835164 - 10,000(.794890271)
P = 430,983.52 - 397,445.14
P = PℎP 33,538.38
R = 10,000
m = 4
r = 8% =
0.08
t = 5
m 4
n = mt = (4)(5)
= 20
P = R - - R
i = = =

89. ROMADEL R. PERALTA
SUBJECT TEACHER
GENERAL MATHEMATICS
STOCKS AND
BONDS

91. STOCKS

92. STOCKS
Stocks are shares in the ownership of the company.
= 1/100
TWO TYPES OF STOCK
Preferred Stock

93. Common Stock
- Right to vote to
shareholders
- Not a priority over the
company’s income
100 shares
- Priority over
the company’s
- No right to

94. Definition of Terms in Relation to Stocks
Stocks are shares in the ownership of the company.
Dividend - are shares in the company’s profit.
Dividend Per Share – ratio of the dividends to the number of shares
Stock market – a place where the stocks can be bought or sold. The stock
market in the Philippines is governed by the Philippines
Stock Exchange (PSE).
Market Value – the current price of a stock at which it can be sold.
Stock Yield Ratio – ratio of the annual dividend per share and the market
value per share. Also called current stock yield.

95. Par Value – the per-share amount as stated on the company certificate.
Unlike the market value, it is determined by the company
and remains stable over time.

96. you know
…
Php 1,434.00/share
Php 122.10/share
Php 985.00/share
Php 177.70/share
Php 785.00/share
Php 207.84/share
Php 1,050.33/share
Di
d

97. BONDS

98. Bonds
Php 1,000,000
Face Value is P1,000,000
Maturity is 5 years
Coupon Rate is 7%
Php 70,000
Mr. Yu
Company Z

99. DEFINITION OF TERMS
Bond - interest-bearing security which promises to pay
(a) Is stated amount of money on the maturity date, and
(b) Regular interest payments called coupons
Coupon - periodic interest payment that the bondholder receives during the time
between purchase date and maturity date; usually received semi-
annually.
Coupon Rate - a rate per coupon payment period, denoted by r.
Price of a Bond - the price of the bond at purchase time; denoted by P.