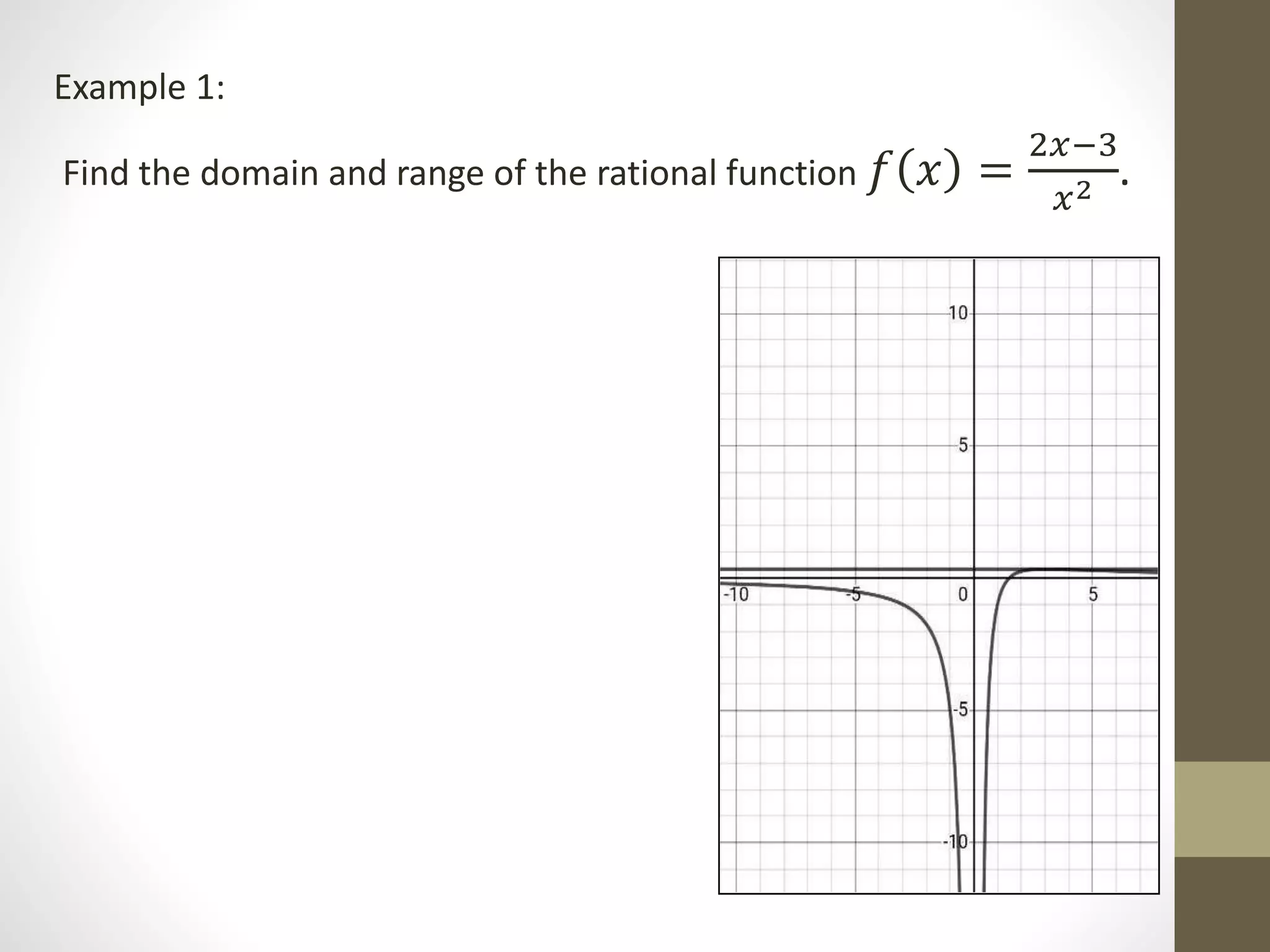
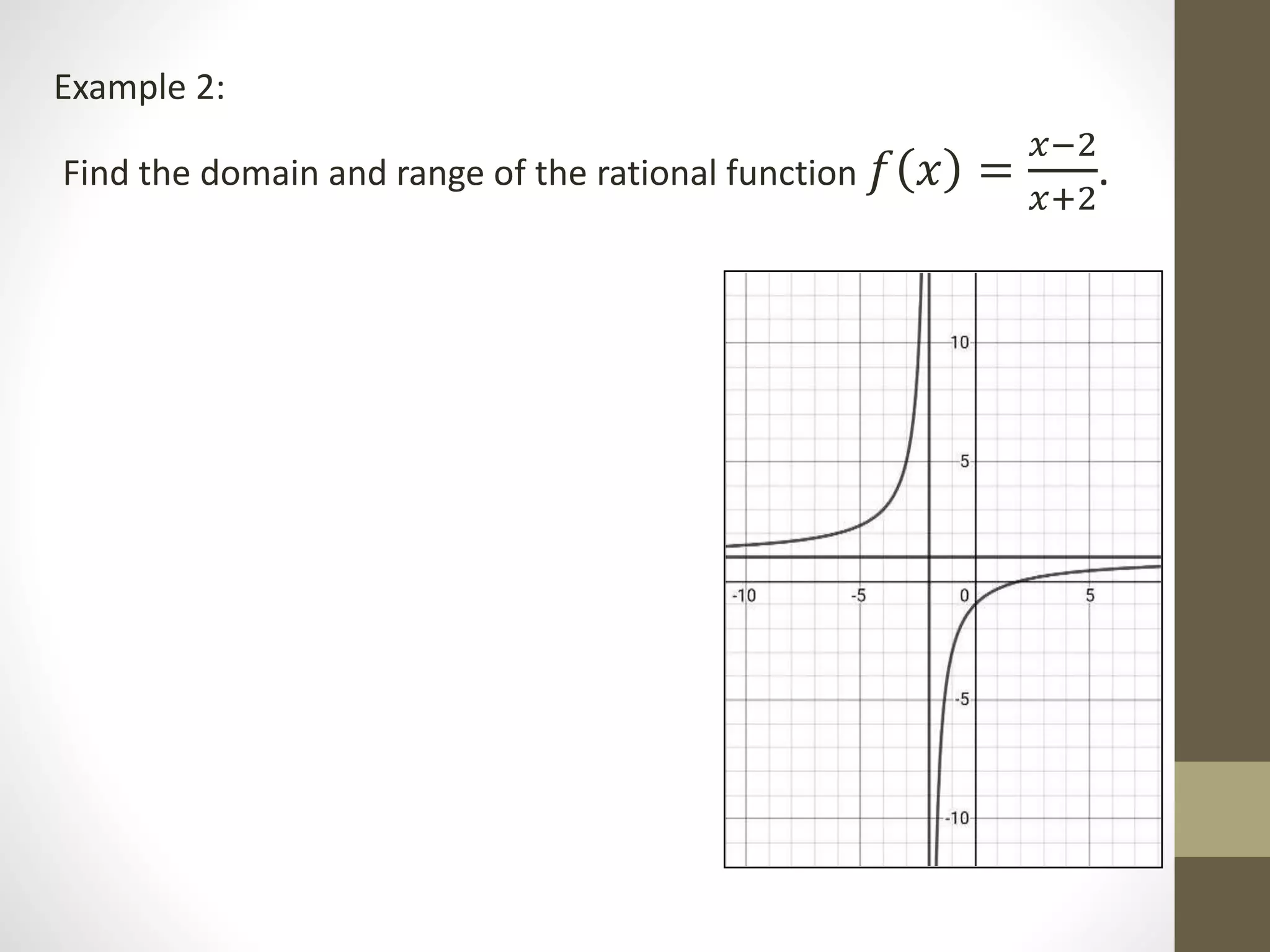
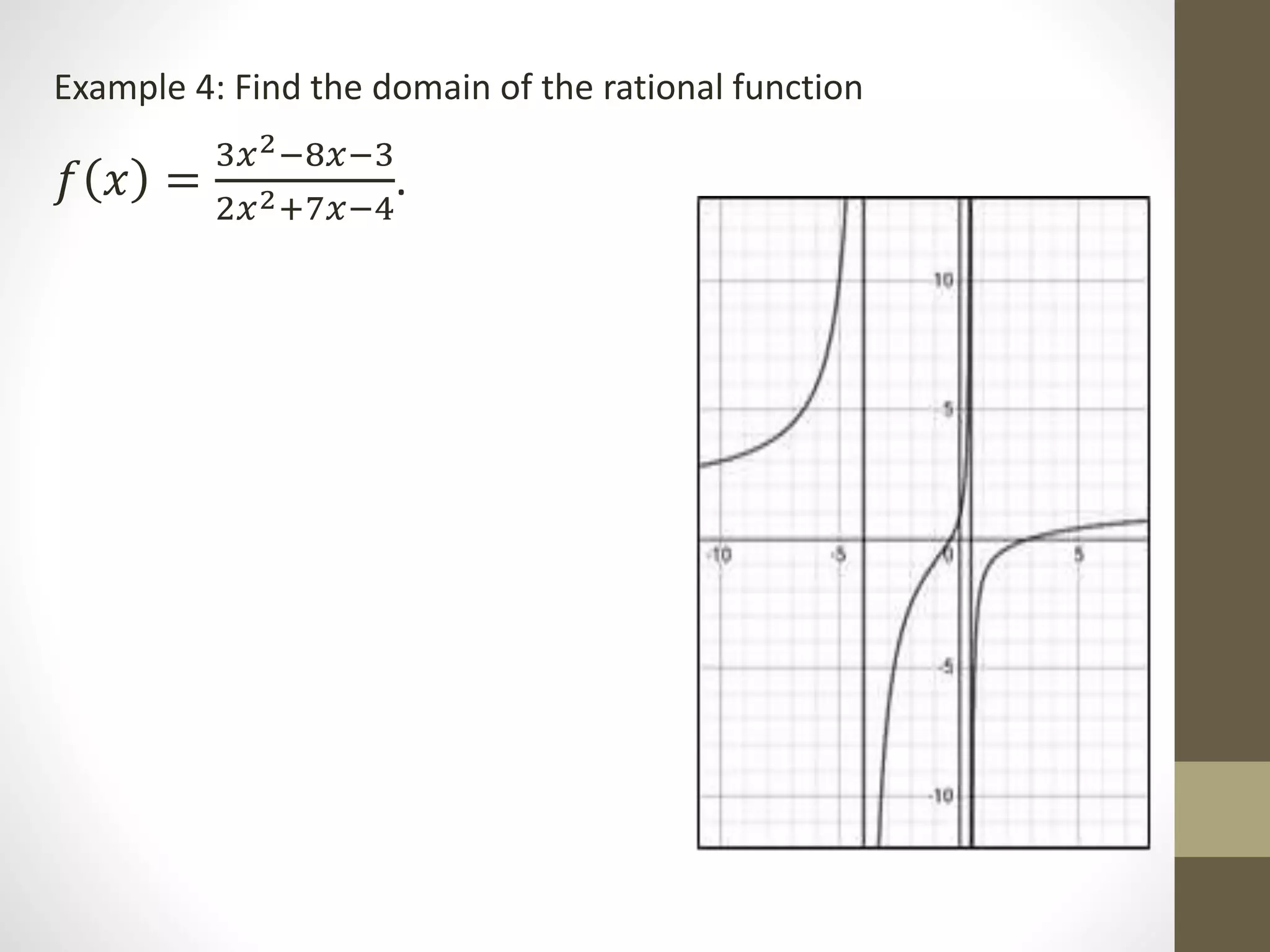
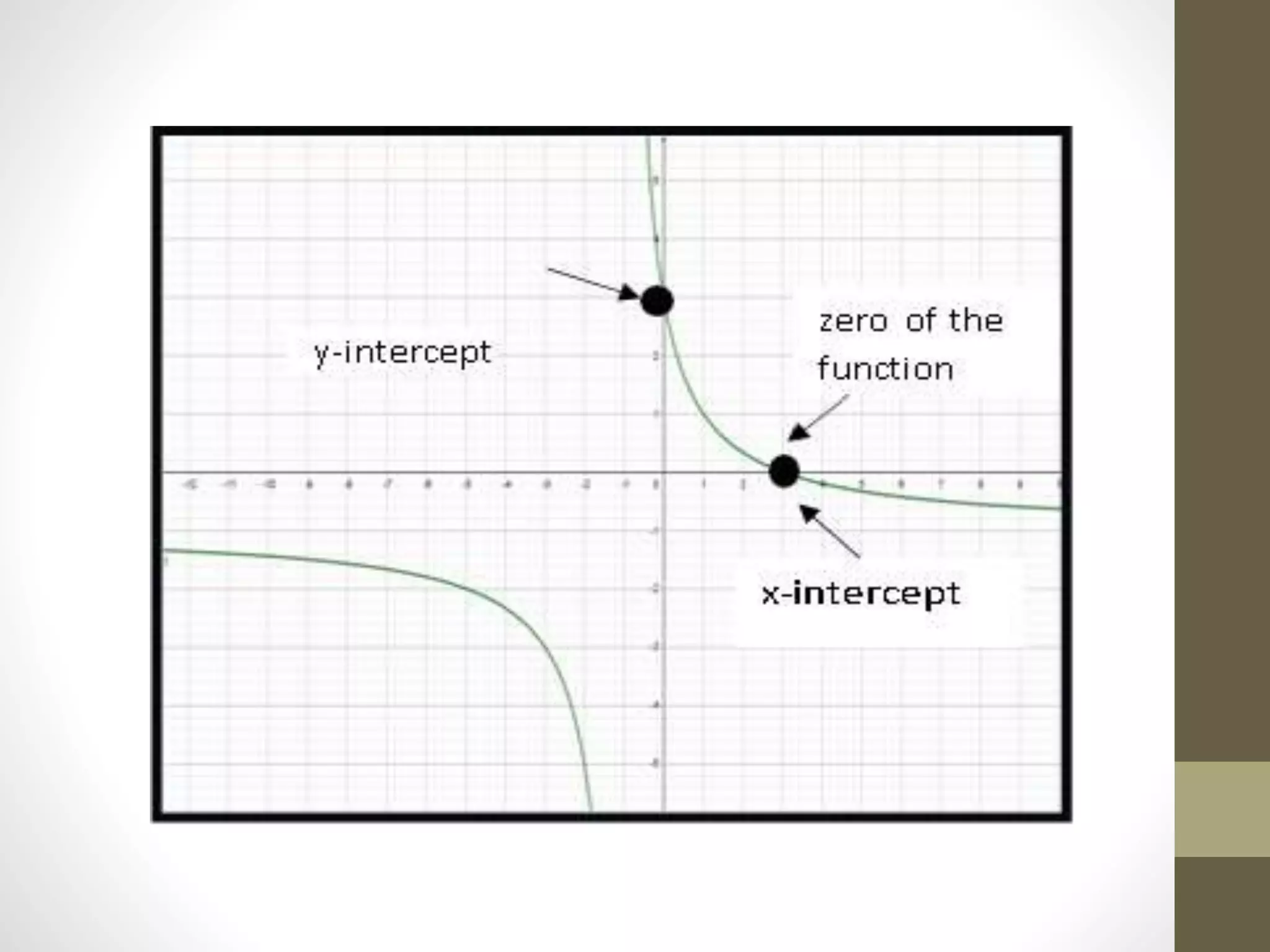
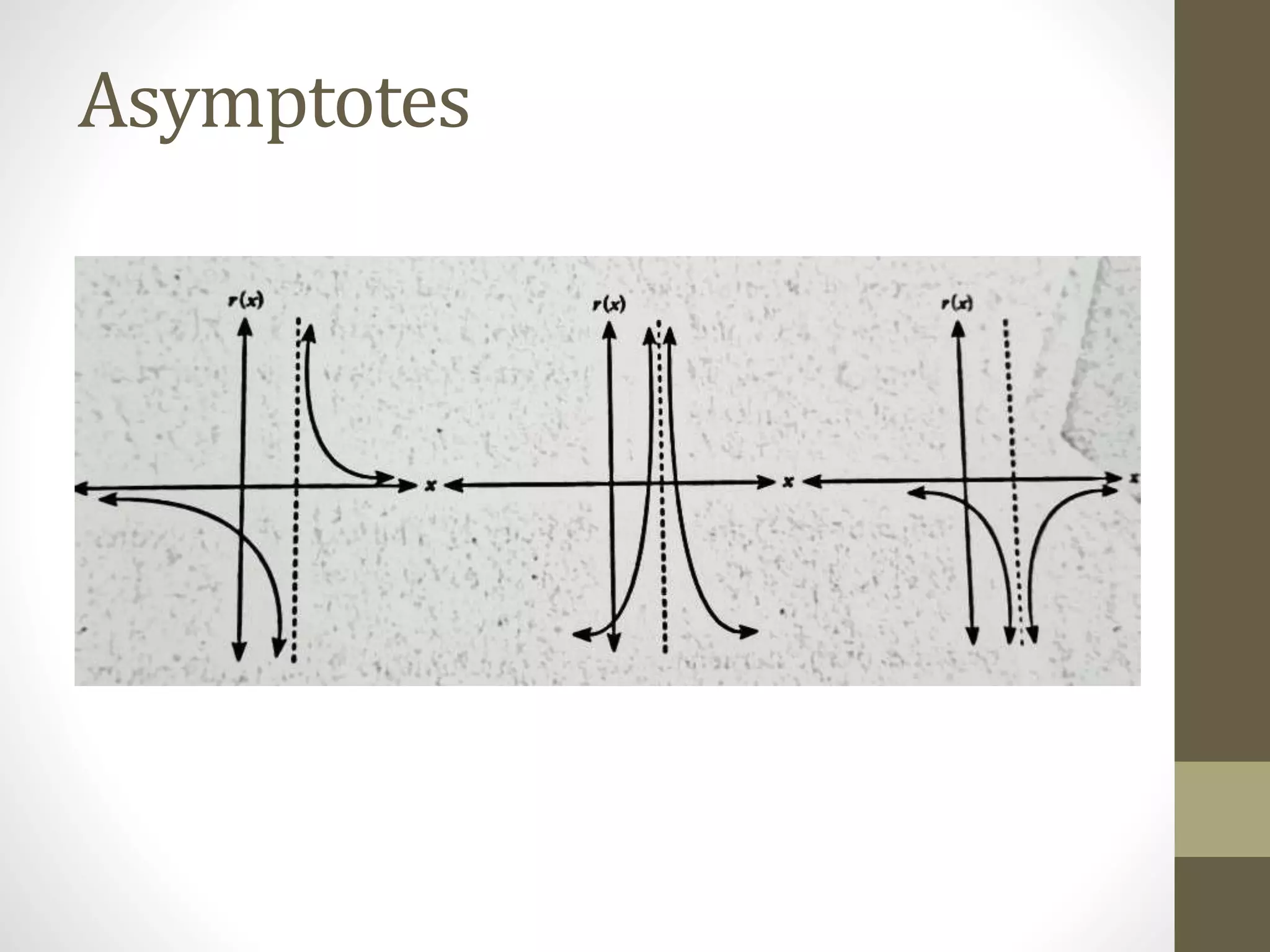
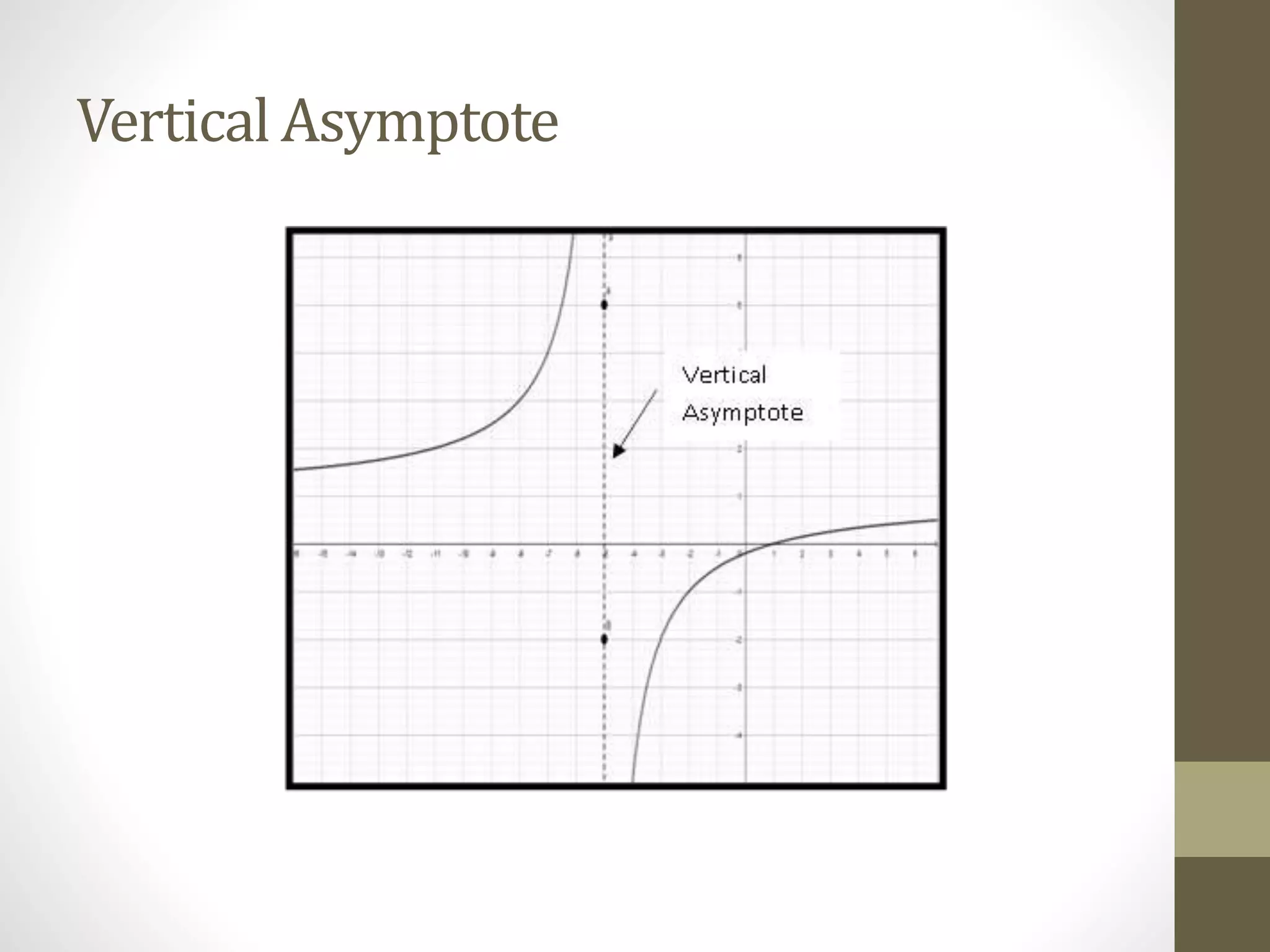
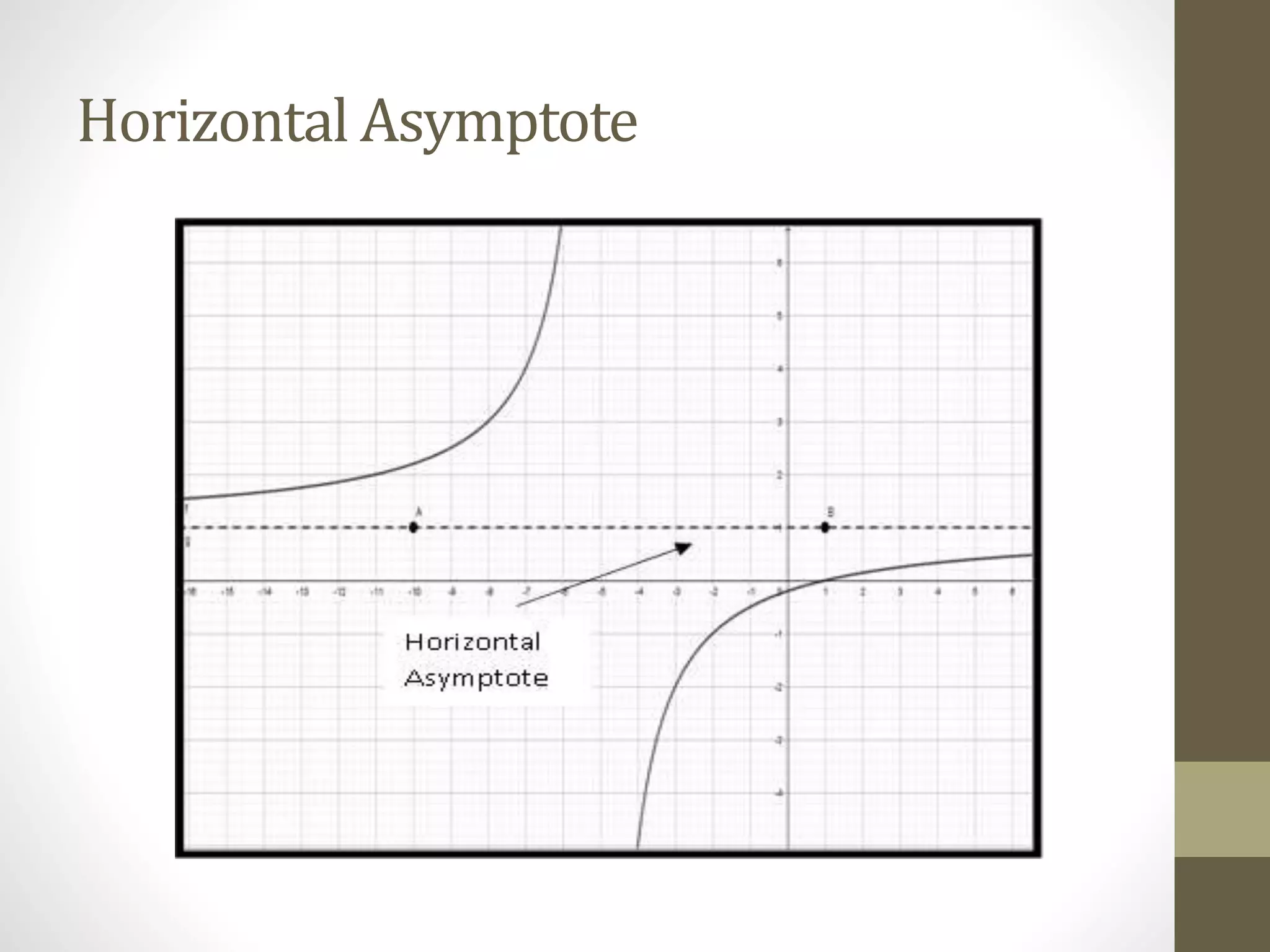
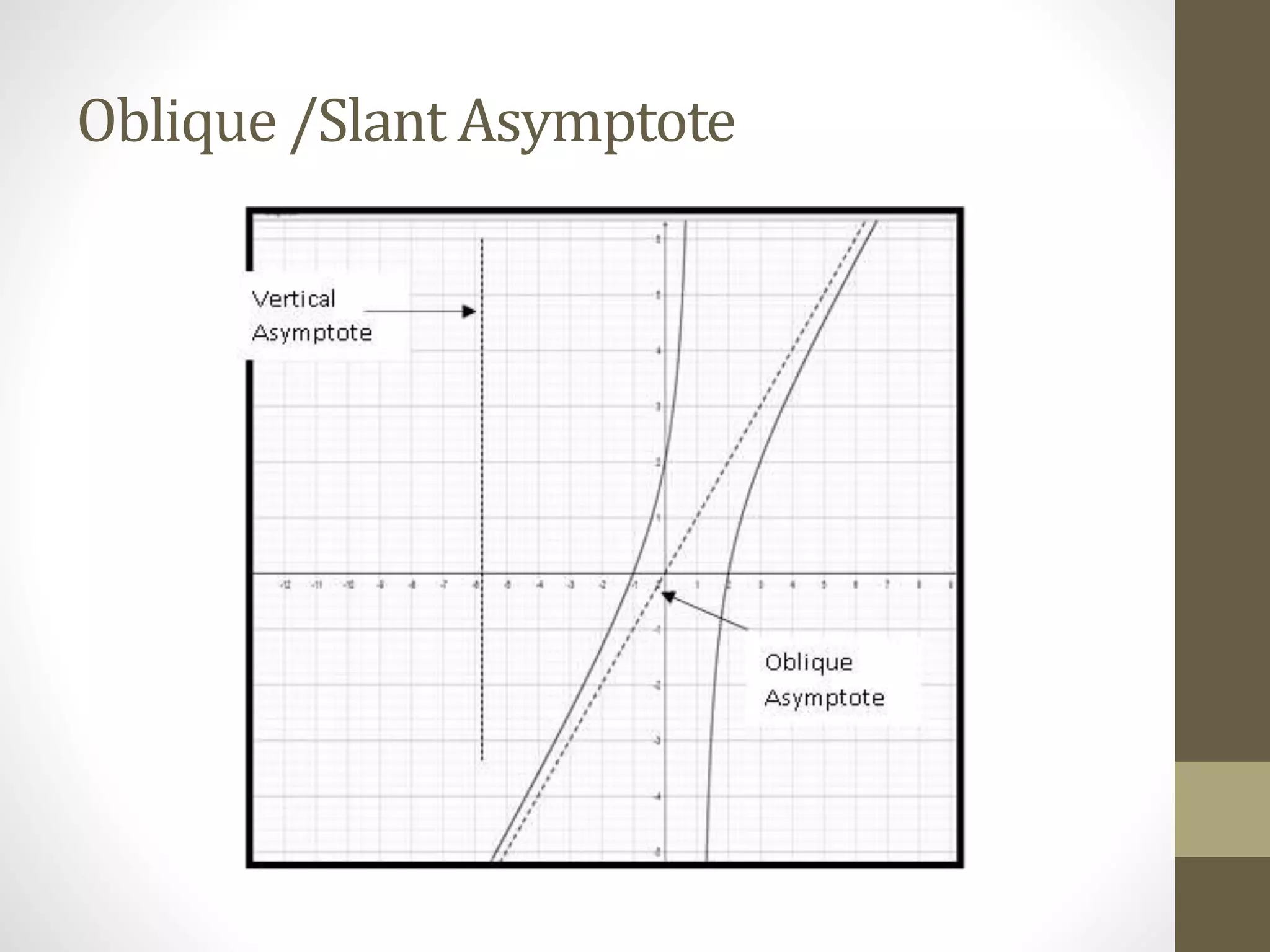
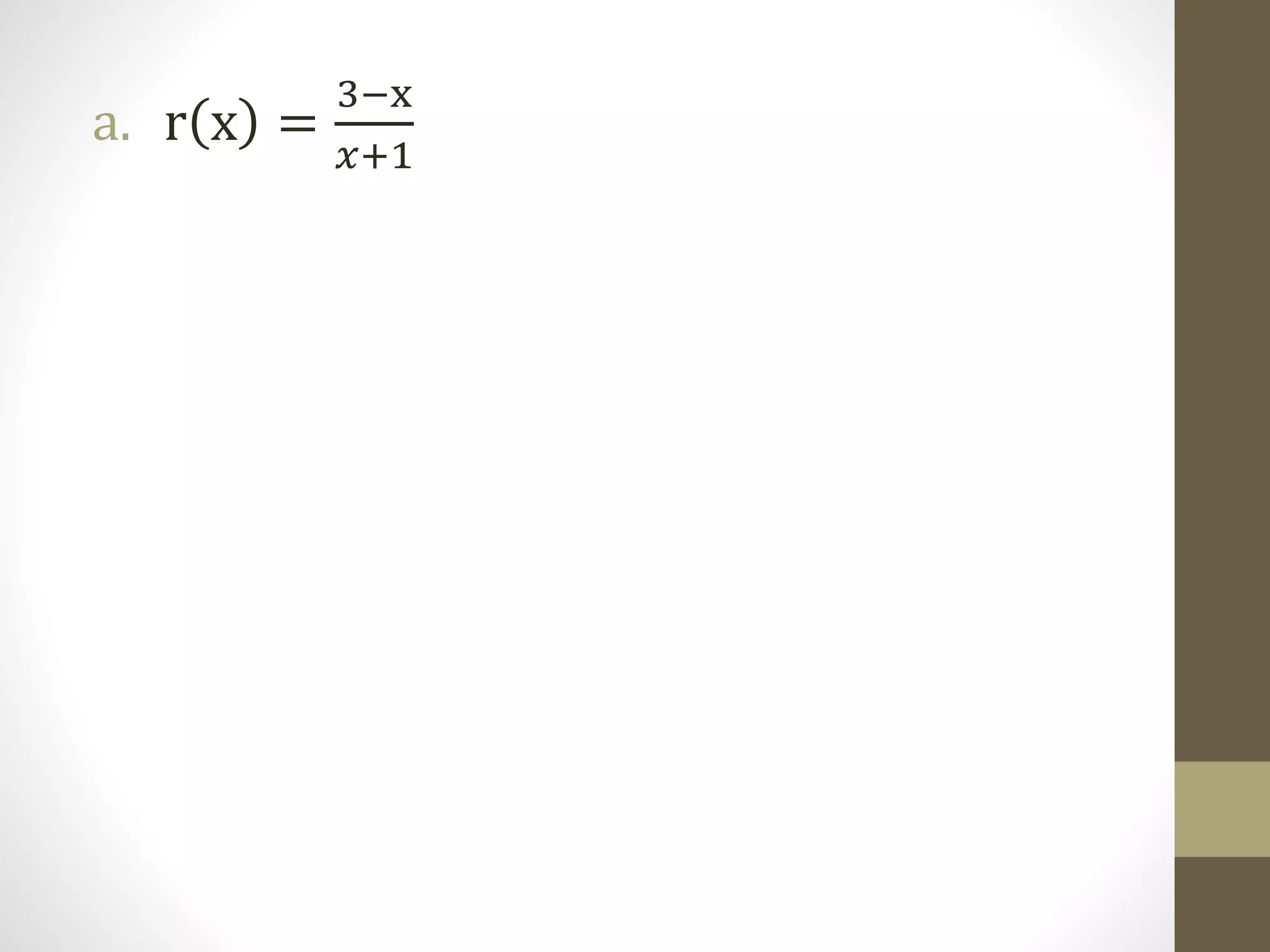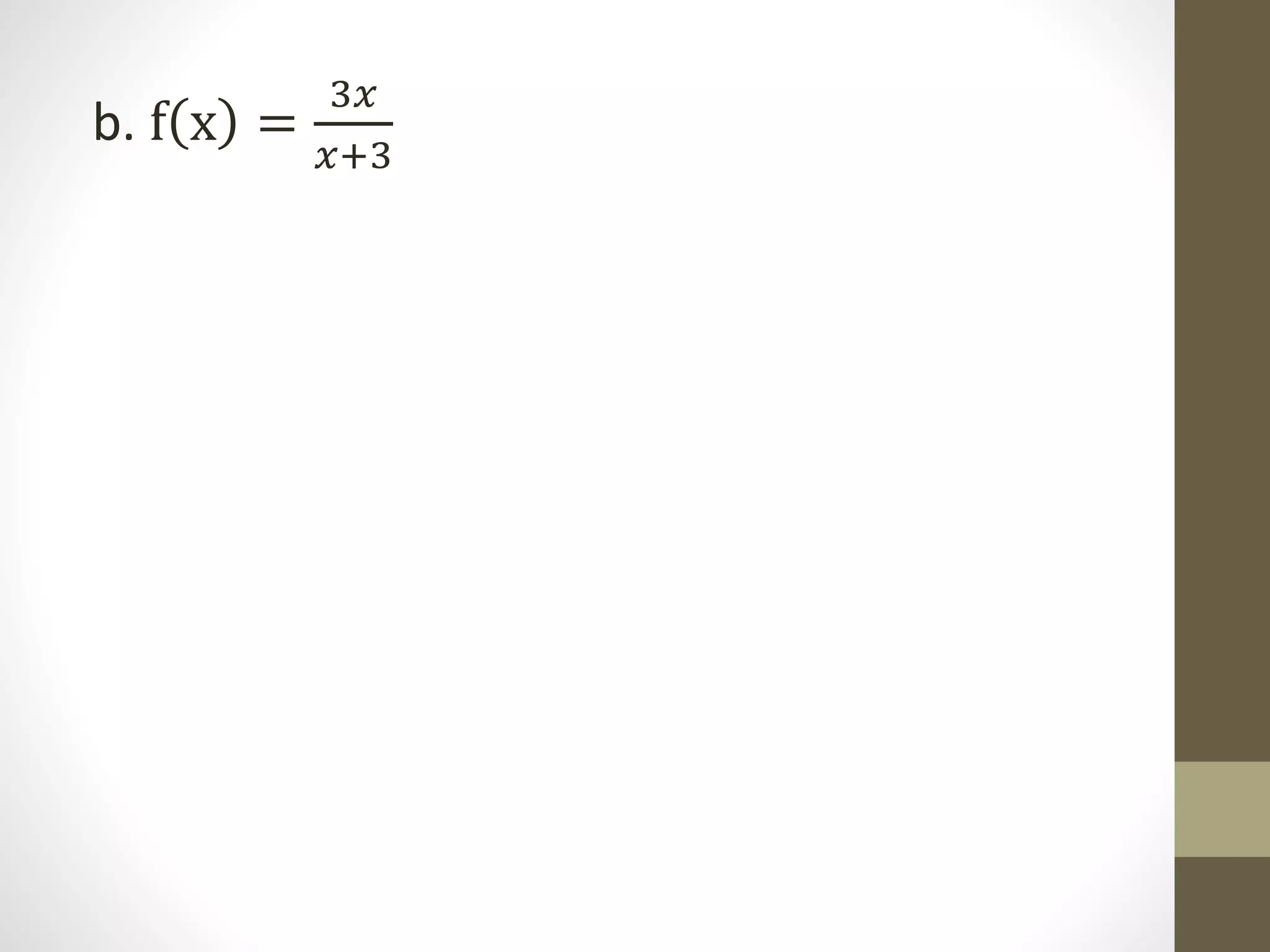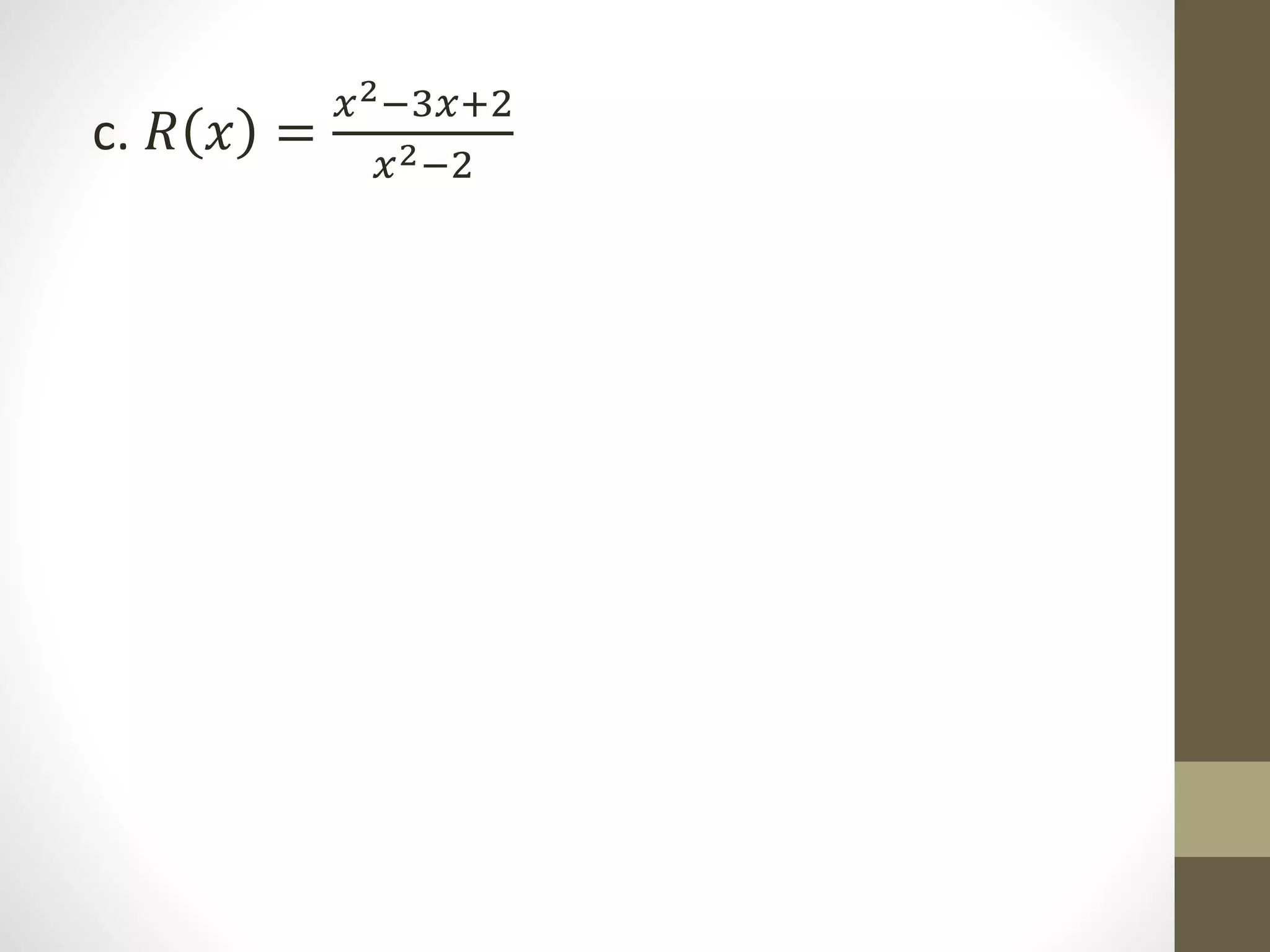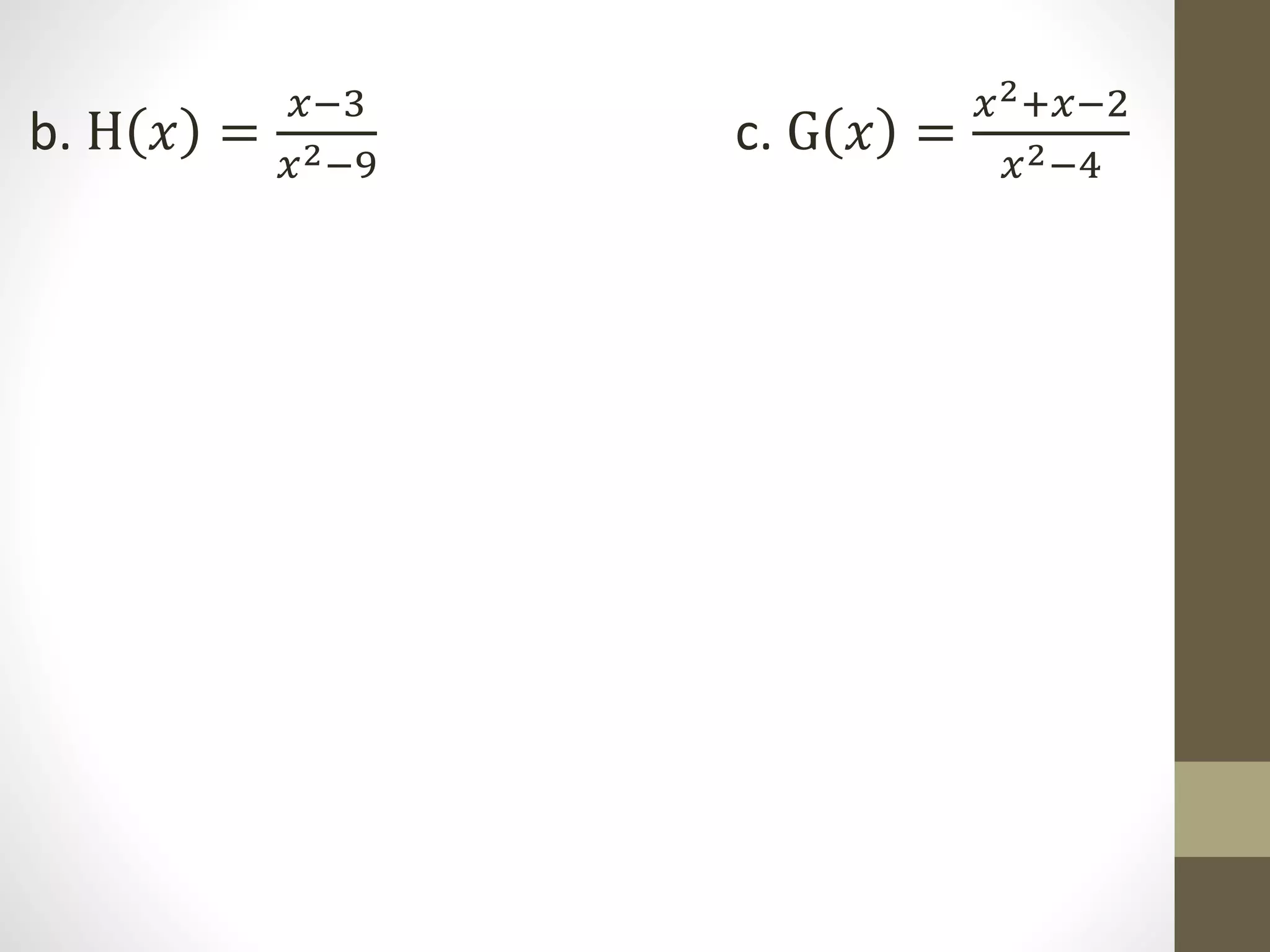The document provides examples of determining the domain and range of rational functions, finding intercepts, zeroes and asymptotes of rational functions, and solving real-life problems involving rational functions, equations, and inequalities. It includes examples of finding the vertical and horizontal asymptotes of rational functions, using long division to determine an oblique asymptote, and writing functions to represent relationships between variables in word problems involving speed, perimeter, budget allocation, and more.

1. DomainandRangeofa
RationalFunctions

2. Example 1:
Find the domain and range of the rational function 𝑓 𝑥 =
2𝑥−3
𝑥2 .

3. Example 2:
Find the domain and range of the rational function 𝑓 𝑥 =
𝑥−2
𝑥+2
.

4. Example 3: Find the domain and range of the rational function
𝑓 𝑥 =
𝑥2 − 3𝑥 − 4
𝑥 + 1

5. Example 4: Find the domain of the rational function
𝑓 𝑥 =
3𝑥2−8𝑥−3
2𝑥2+7𝑥−4
.

6. Intercepts,Zeroes,and
AsymptotesoftheRational
Functions

7. Which of the following is an example of rational function?
𝑓 𝑥 =
3𝑥2+1
𝑥−1
𝑥
3
=
8
3
1
3𝑥−1
+ 3 < 0
Find the domain and range of the functions
𝑓 𝑥 =
𝑥
𝑥+3
𝑓 𝑥 =
3
𝑥−4

8. The intercepts of the graph of a rational function are the
points of intersection of its graph and an axis.
 The y-intercepts of the graph of a rational function 𝑟(𝑥), it is
exists, occurs 𝑎𝑡 𝑟(0), provided that 𝑟(𝑥) is defined at 𝑥 = 0.
The x-intercepts of the graph of a rational function 𝑟(𝑥), it is
exists, occurs at the zeroes of the numerator that are not
zeroes of the denominators.
The zeroes of a function are values of x which make the
function zero. The numbered zeroes are also x-intercepts of
the graph of the function.

10. Example:
Find the x- and y- intercepts , of the following
rational functions.
a. r x =
3−x
𝑥+1
b. f x =
3𝑥
𝑥+3
c. 𝑅 𝑥 =
𝑥2−3𝑥+2
𝑥2−2

11. a. r x =
3−x
𝑥+1

12. b. f x =
3𝑥
𝑥+3

13. c. 𝑅 𝑥 =
𝑥2−3𝑥+2
𝑥2−2

14. Find the zeroes of the ff rational functions.
a. g 𝑥 =
𝑥−2
𝑥+6
b. H 𝑥 =
𝑥−3
𝑥2−9
c. G 𝑥 =
𝑥2+𝑥−2
𝑥2−4

15. b. H 𝑥 =
𝑥−3
𝑥2−9
c. G 𝑥 =
𝑥2+𝑥−2
𝑥2−4

16. Asymptotes
imaginary line to which a graph gets closer and closer as it
increases or decreases its value without limit.
Kinds of Asymptote
 Vertical Asymptote
Horizontal Asymptote
Oblique/Slant Asymptote

17. Asymptotes

18. Vertical Asymptote

19. Example:
Determine the vertical asymptotes of each rational
functions.
a. r x =
𝑥−1
𝑥+5
b. 𝑅 x =
2x2−x+1
𝑥2−6𝑥+9
c. ℎ x =
(𝑥+1)(𝑥−3)(𝑥+4)
(𝑥−1)(𝑥+2)

20. Horizontal Asymptote

21. To determine the horizontal asymptote of a rational function,
compare the degree of the numerator n and the degree of the
denominator d.
i. If 𝑛 < 𝑑 , the horizontal asymptote is 𝑦 = 0.
ii. If 𝑛 = 𝑑, the horizontal asymptote 𝑦 is the ratio of the leading
coefficient of the numerator 𝑎𝑛 to the leading coefficient of the
denominator 𝑎𝑑. That is y =
𝑎𝑛
𝑎𝑑
.
iii. If 𝑛 > 𝑑, there is no horizontal asymptote.

22. Example:
Determine the horizontal asymptotes of each
rational functions.
a. r x =
𝑥
9𝑥2−1
b. 𝑅 x =
7−3x
2𝑥+1
c. ℎ x =
4𝑥4−1
1−𝑥2

23. Oblique /Slant Asymptote

24. Oblique /Slant Asymptote
 To find slant asymptote simply divide the
numerator by the denominator by either using
long division or synthetic division. The oblique
asymptote is the quotient with the remainder
ignored and set equal to y.
Example:
ℎ 𝑥 =
𝑥2 + 3
𝑥 − 1

26. Example:
Determine the vertical and horizontal asymptote of
the rational function: 𝑟 𝑥 =
4𝑥−1
3−2𝑥
y-intercept:
x-intercept:
Zero of the denominator:
Zero of the numerator:
Vertical asymptote:
x
−
1
2
−
1
4
1
2
1 7
4
5
4
9
4
𝑅(𝑥)
−
3
4
−
4
7
1
2
3 -12
−
1
2
−
16
3

28. SolvingReal-LifeProblems
InvolvingRationalFunctions,
Equations,andInequalities

29. Example 1:
Mayor Rodriguez received 5000 sacks of rice to be distributed
among the families in his municipality during the lockdown. If the
municipality has x families, write the function which represents the
relationship of the allotted sack of rice per family(y-variable) versus
the total number of families

30. Example2:
To beat the heat of summer, Mang Berto built a rectangular
swimming pool that has a perimeter of 200 meters. Write the
function which represents the width(y) of the swimming pool as a
function of the length(x).

31. Example 3:
Mario rides his motorcycle in going to school. He drives at an
average speed of 30 kilometers per hour. The distance between his
house and the school is 15 kilometers. Every time he sees his best
friend Jessica walking on the road, he invites her for a ride and lowers
his speed. On the other hand, he increases his speed when he wakes
up late for school.
15 kilometers

32. a. How long does it take Mario to reach school considering his
average speed?

33. b. If x represents the time it takes Mario to drive to school with the
given distance of 15 kilometers, how will you represent the relationship
of his speed (y) versus the time (x)?

34. c. Mario’s average speed as 30 kilometers per hour. Suppose Mario
lowers his speed by 10 kilometers per hour, how long will he reach the
school given the same distance?

35. D. Suppose Mario’s speed is unknown and represented by (x), he
lowers his speed by 10 kilometers per hour at a distance of 15
kilometers and reaches school at
3
4
hours. How will you write the
equation to find his average speed (x)?

36. Example 4:
Bamban National High School is preparing for its 25th founding
anniversary. The chairperson of the activity allocated ₱90,000.00 from
different stakeholders to be divided among various committees of the
celebration. Construct a function 𝐶(𝑛) which would give the amount of
money each of the 𝑛 numbers of committees would receive. If there are six
committees, how much would each committee have?

38. Example 5:
Barangay Masaya allocated a budget amounting to
₱100,000.00 to provide relief goods for each family in the
barangay due to the Covid-19 pandemic situation. The amount
is to be allotted equally among all the families in the barangay.
At the same time a philanthropist wants to supplement this
budget and he allotted an additional ₱500.00 to be received by
each family. Write an equation representing the relationship
of the allotted amount per family (y-variable) versus the total
number of families (x-variable). How much will be the amount
of each relief packs if there are 200 families in the barangay?