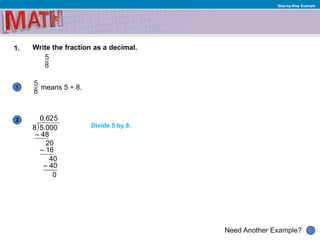
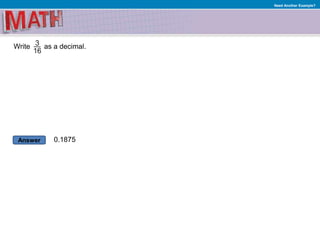
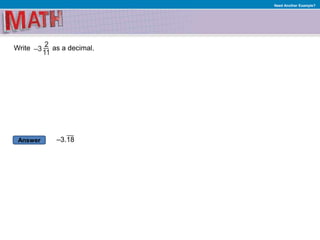
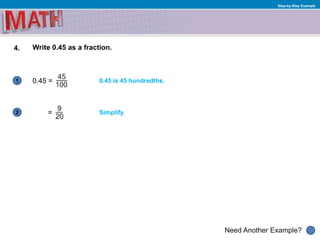
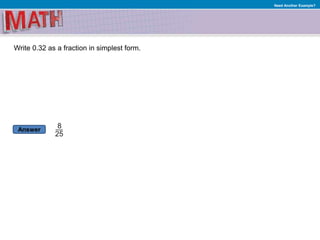
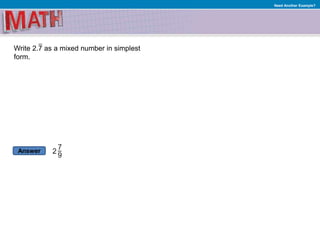
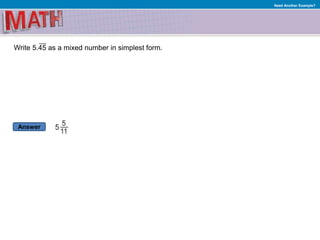
This document contains a mathematics lesson on writing numbers in different forms, including: 1. Converting fractions to decimals and decimals to fractions 2. Examples of solving proportions and writing decimals as fractions 3. The lesson discusses why it is helpful to write numbers in different ways, such as for measurements or when dealing with money.

1. Course 3, Lesson 1-1
Add, subtract, multiply, or divide.
1. –24 + 17 2. 37 – (–14)
3. (–7)(–12) 4. 120 ÷ (–20)
Solve each proportion.
5. 6.
7. Mila can join a health club and pay $135 for three
months. At this rate, how much would a membership
for 12 months cost?

3
12 4
p

24
32 8
x

2. Course3, Lesson 1-1
ANSWERS
1. –7
2. 51
3. 84
4. –6
5. 9
6. 6
7. $540

3. WHY is it helpful to write numbers in
different ways?
The Number System
Course 3, Lesson 1-1

4. Course 3, Lesson 1-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council
of Chief State School Officers. All rights reserved.
The Number System
• 8.NS.1
Know that numbers that are not rational are called irrational.
Understand informally that every number has a decimal expansion; for
rational numbers show that the decimal expansion repeats eventually,
and convert a decimal expansion which repeats eventually into a
rational number.

5. Course 3, Lesson 1-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council of
Chief State School Officers. All rights reserved.
The Number System
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
6 Attend to precision.
7 Look for and make use of structure.
8 Look for and express regularity in repeated reasoning.

6. To
• write fractions as decimals
• write decimals as fractions
Course 3, Lesson 1-1
The Number System

7. • rational number
• repeating decimal
• terminating decimal
Course 3, Lesson 1-1
The Number System

8. Course 3, Lesson 1-1
The Number System
Words A rational number is a number that can be written as the
ratio of two integers in which the denominator is not zero.
Symbols , where a and b are integers and b ≠ 0
Model
a
b

9. 1
Need Another Example?
2
Step-by-Step Example
1. Write the fraction as a decimal.
means 5 ÷ 8.
0.6
5.000
– 48
20
– 16
40
– 40
0
8 Divide 5 by 8.
25

10. Answer
Need Another Example?
Write as a decimal.
0.1875

11. 1
Need Another Example?
2
3
Step-by-Step Example
2. Write the mixed number as a decimal.
can be rewritten as .
Divide 5 by 3 and add a
negative sign.
The mixed number can be written as –1.6.

12. Answer
Need Another Example?
Write as a decimal.
–3.18

13. 1
Need Another Example?
2
3
4
Step-by-Step Example
3. In a recent season, St. Louis Cardinals first
baseman Albert Pujols had 175 hits in 530 at bats.
To the nearest thousandth, find his batting average.
To find his batting average, divide the number of hits, 175,
by the number of at bats, 530.
175
Look at the digit to the right of the thousandths place.
Since 1 < 5, round down.
530 0.3301886792
Albert Pujols’s batting average was 0.330.

14. Answer
Need Another Example?
When Juliana went strawberry picking, 28 of
the 54 strawberries she picked weighed less
than 2 ounces. To the nearest thousandth, find
the fraction of the strawberries that weighed
less than 2 ounces.
0.519

15. 1
Need Another Example?
2
Step-by-Step Example
4. Write 0.45 as a fraction.
0.45 =
=
0.45 is 45 hundredths.
Simplify.

16. Answer
Need Another Example?
Write 0.32 as a fraction in simplest form.

17. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
5. Write 0.5 as a fraction in simplest form.
Assign a variable to the value 0.5. Let N = 0.555... . Then
perform operations on N to determine its fractional value.
N = 0.555...
Simplify.
Multiply each side by 10 because 1 digit repeats.
7
10(N) = 10(0.555...)
Multiplying by 10 moves the decimal point
1 place to the right.
10N = 5.555...
–N = 0.555... Subtract N = 0.555... to eliminate the repeating part.
Divide each side by 9.
9N = 5
N =
The decimal 0.5 can be written as .

18. Answer
Need Another Example?
Write 2.7 as a mixed number in simplest
form.

19. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
6. Write 2.18 as a mixed number in simplest form.
Assign a variable to the value 2.18. Let N = 2.181818….
Then perform operations on N to determine its fractional value.
N = 2.181818...
Simplify.
Multiply each side by 100 because 2 digits repeat.100(N) = 100(2.181818...)
Multiplying by 100 moves the decimal point
2 places to the right.
100N = 218.181818
–N = 2.181818… Subtract N = 2.181818… to eliminate the repeating part.
Divide each side by 99. Simplify.
99N = 216
N =
7 The decimal 2.18 can be written as .

20. Answer
Need Another Example?
Write 5.45 as a mixed number in simplest form.

21. How did what you learned
today help you answer the
WHY is it helpful to write numbers in
different ways?
Course 3, Lesson 1-1
The Number System

22. How did what you learned
today help you answer the
WHY is it helpful to write numbers in
different ways?
Course 3, Lesson 1-1
The Number System
Sample answers:
• In some cases, like when using money, you may need
to write a fraction as a decimal.
• When you are using standard measurements like feet
or inches, you may need to write a decimal as a
fraction.

23. Write as a decimal.
Ratios and Proportional RelationshipsThe Number System
5
6
Course 3, Lesson 1-1