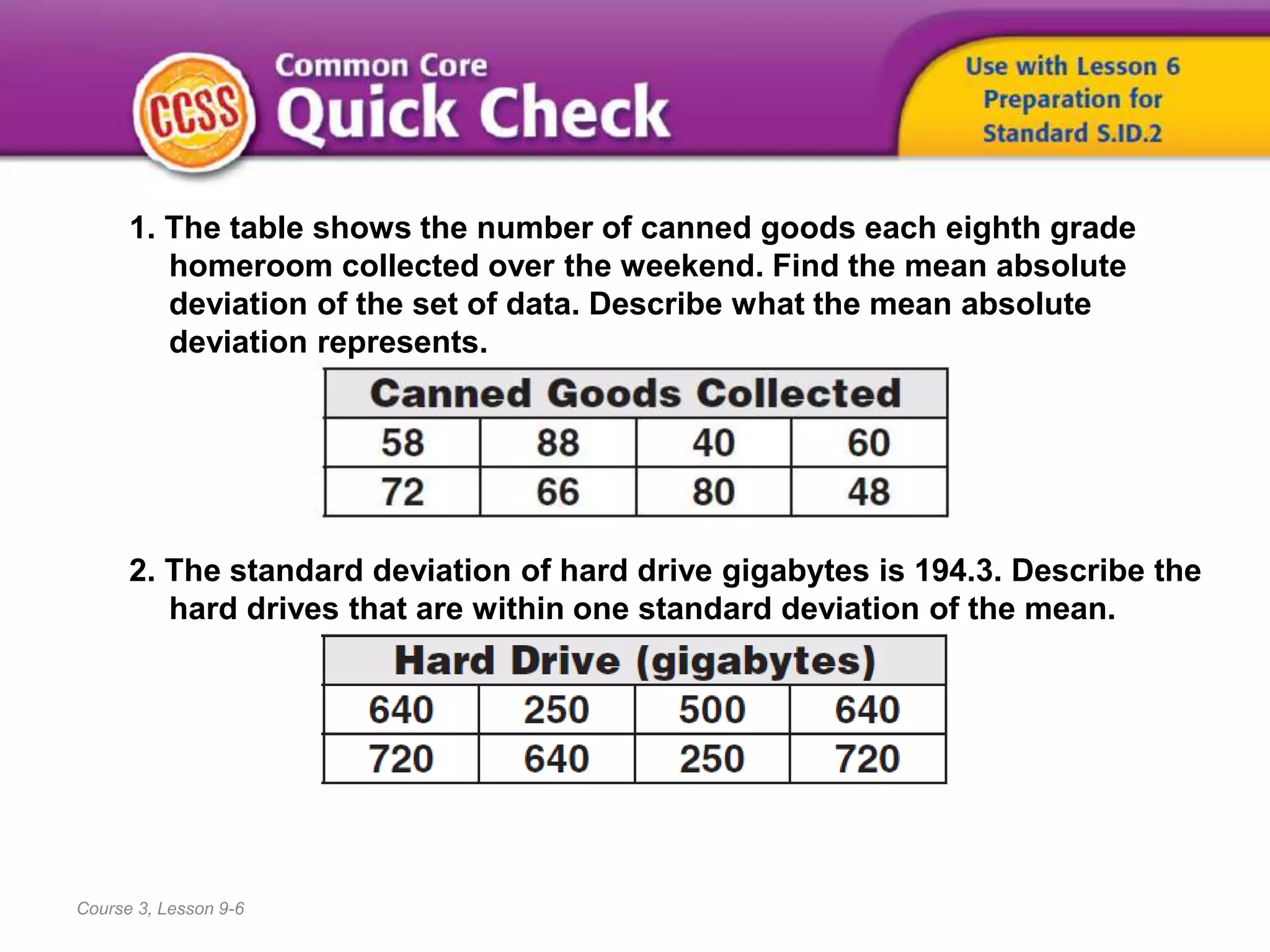
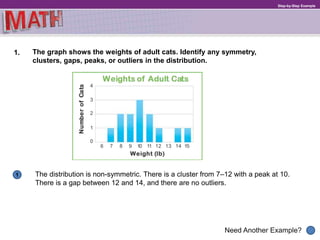
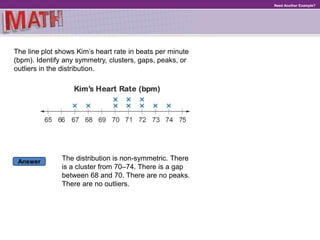
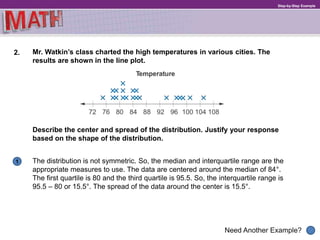
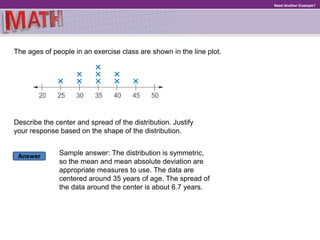
The document provides examples and explanations for describing distributions of data sets. It discusses identifying symmetry, clusters, gaps, peaks, and outliers. It explains that the median and interquartile range should be used to describe the center and spread of non-symmetric distributions, while the mean and mean absolute deviation can describe symmetric distributions. Students are told that patterns in distributions help compare two quantities and that describing distributions involves noting their shape, center, and spread.

1. Course 3, Lesson 9-6
1. The table shows the number of canned goods each eighth grade
homeroom collected over the weekend. Find the mean absolute
deviation of the set of data. Describe what the mean absolute
deviation represents.
2. The standard deviation of hard drive gigabytes is 194.3. Describe the
hard drives that are within one standard deviation of the mean.

2. Course 3, Lesson 9-6
ANSWERS
1. 12.5; This means that the average distance each data value is from
the mean is 12.5 canned goods.
2. Hard drives that are between 350.7 and 739.3 gigabytes are with one
standard deviation of the mean.

3. HOW are patterns used
when comparing two quantities?
Statistics and Probability
Course 3, Lesson 9-6

4. Course 3, Lesson 9-6 Common Core State Standards © Copyright 2010. National Governors Association Center for
Best Practices and Council of Chief State School Officers. All rights reserved.
Statistics and Probability
• Preparation for S.ID.2
Use statistics appropriate to the shape of the data distribution to
compare center (median, mean) and spread (interquartile range,
standard deviation) of two or more different data sets.
• Preparation for S.ID.3
Interpret differences in shape, center, and spread in the context of the
data sets, accounting for possible effects of extreme data points
(outliers).

5. Course 3, Lesson 9-6 Common Core State Standards © Copyright 2010. National Governors Association Center for
Best Practices and Council of Chief State School Officers. All rights reserved.
Statistics and Probability
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.

6. To
• describe the distribution of a
set of data
Course 3, Lesson 9-6
Statistics and Probability

7. • distribution
• symmetric
Course 3, Lesson 9-6
Statistics and Probability

8. 1
Need Another Example?
Step-by-Step Example
1. The graph shows the weights of adult cats. Identify any symmetry,
clusters, gaps, peaks, or outliers in the distribution.
The distribution is non-symmetric. There is a cluster from 7–12 with a peak at 10.
There is a gap between 12 and 14, and there are no outliers.

9. Answer
Need Another Example?
The line plot shows Kim’s heart rate in beats per minute
(bpm). Identify any symmetry, clusters, gaps, peaks, or
outliers in the distribution.
The distribution is non-symmetric. There
is a cluster from 70–74. There is a gap
between 68 and 70. There are no peaks.
There are no outliers.

10. 1
Need Another Example?
Step-by-Step Example
2. Mr. Watkin’s class charted the high temperatures in various cities. The
results are shown in the line plot.
The distribution is not symmetric. So, the median and interquartile range are the
appropriate measures to use. The data are centered around the median of 84°.
The first quartile is 80 and the third quartile is 95.5. So, the interquartile range is
95.5 – 80 or 15.5°. The spread of the data around the center is 15.5°.
Describe the center and spread of the distribution. Justify your response
based on the shape of the distribution.

11. Answer
Need Another Example?
The ages of people in an exercise class are shown in the line plot.
Describe the center and spread of the distribution. Justify
your response based on the shape of the distribution.
Sample answer: The distribution is symmetric,
so the mean and mean absolute deviation are
appropriate measures to use. The data are
centered around 35 years of age. The spread of
the data around the center is about 6.7 years.

12. How did what you learned
today help you answer the
How are patterns used
when comparing two quantities?
Course 3, Lesson 9-6
GeometryStatistics and Probability

13. How did what you learned
today help you answer the
How are patterns used
when comparing two quantities?
Course 3, Lesson 9-6
GeometryStatistics and Probability
Sample answers:
• Certain patterns like symmetry, clusters, gaps, or peaks
help to describe data sets.
• The description of symmetry can decide which
measures of center and spread to use to describe the
data set.

14. Make a sketch of a bar graph
that is symmetric. Describe
any clusters, gaps, peaks,
and outliers in your graph.
Course 3, Lesson 9-6
Ratios and Proportional RelationshipsFunctionsStatistics and Probability