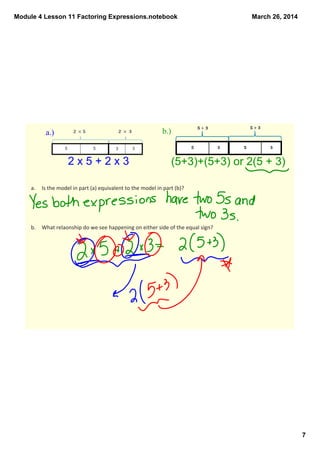
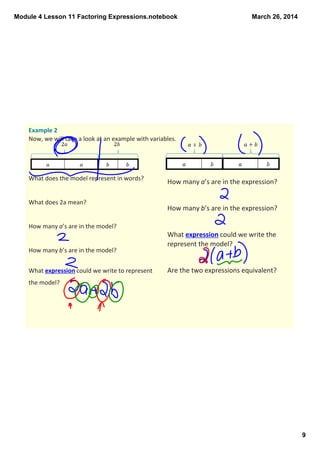
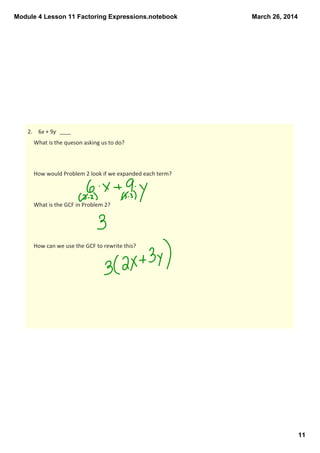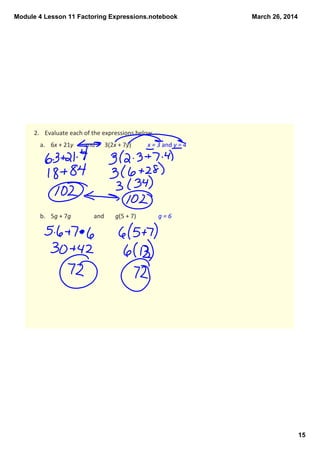This document provides instruction on factoring expressions using the greatest common factor (GCF) and the distributive property. It includes examples of factoring expressions with variables like 3f + 3g and 6x + 9y. Students are asked to identify the GCF of expressions and use it to write equivalent expressions. They are given exercises to factor expressions and evaluate equivalent expressions for given variable values. The document aims to teach students how to move between expanded and factored forms of expressions.

1. Module 4 Lesson 11 Factoring Expressions.notebook
1
March 26, 2014
Problem Set Lesson 10 Answers

2. Module 4 Lesson 11 Factoring Expressions.notebook
2
March 26, 2014
MODULE 4 Expressions and Equaons
Topic C: Replacing Leer and Numbers
Lesson 11 Factoring Expressions
Student Outcomes
§ Students model and write equivalent expressions using the distribuve property. They move from an
expanded form to a factored form of an expression.
Turn to the sprints so we can review
Greatest Common Factors

3. Module 4 Lesson 11 Factoring Expressions.notebook
3
March 26, 2014
Sprints Round 1

4. Module 4 Lesson 11 Factoring Expressions.notebook
4
March 26, 2014
Sprints Round 2

5. Module 4 Lesson 11 Factoring Expressions.notebook
5
March 26, 2014
Classwork
Example 1
a. Use the model to answer the following quesons.
How many fives are in the model?
How many threes are in the model?
What does the expression represent in words?
What expression could we write to represent the model?

6. Module 4 Lesson 11 Factoring Expressions.notebook
6
March 26, 2014
b. Use the new model and the previous model to answer the next set of quesons.
How many fives are in the model?
How many threes are in the model?
What does the expression represent in words?
What expression could we write to represent the model?
This is the correct model
for your notes.

7. Module 4 Lesson 11 Factoring Expressions.notebook
7
March 26, 2014
a. Is the model in part (a) equivalent to the model in part (b)?
b. What relaonship do we see happening on either side of the equal sign?
a.) b.)
2 x 5 + 2 x 3 (5+3)+(5+3) or 2(5 + 3)

8. Module 4 Lesson 11 Factoring Expressions.notebook
8
March 26, 2014
2 x 5 + 2 x 32(5 + 3) =
e. In 5th grade and in Module 2 of this year, you have used similar reasoning to
solve problems. What is the name of the property that is used to say that

9. Module 4 Lesson 11 Factoring Expressions.notebook
9
March 26, 2014
Example 2
Now, we will take a look at an example with variables.
What does the model represent in words?
What does 2a mean?
How many a’s are in the model?
How many b’s are in the model?
What expression could we write to represent
the model?
How many a’s are in the expression?
How many b’s are in the expression?
What expression could we write the
represent the model?
Are the two expressions equivalent?

10. Module 4 Lesson 11 Factoring Expressions.notebook
10
March 26, 2014
Example 3
Use GCF and the distribuve property to write equivalent expressions.
1. 3f + 3g
What is the queson asking us to do?
How would Problem 1 look if we expanded each term?
What is the GCF in Problem 1?
How can we use the GCF to rewrite this?

11. Module 4 Lesson 11 Factoring Expressions.notebook
11
March 26, 2014
2. 6x + 9y
What is the queson asking us to do?
How would Problem 2 look if we expanded each term?
What is the GCF in Problem 2?
How can we use the GCF to rewrite this?

12. Module 4 Lesson 11 Factoring Expressions.notebook
12
March 26, 2014
3. 3c + 11c
Is there a greatest common factor in Problem 3?
Rewrite the expression using the distribuve property.

13. Module 4 Lesson 11 Factoring Expressions.notebook
13
March 26, 2014
4. 24b + 8
Explain how you used GCF and the distribuve property to rewrite the expression in Problem 4.
Why is there a 1 in the parentheses?
How is this related to the first two examples?

14. Module 4 Lesson 11 Factoring Expressions.notebook
14
March 26, 2014
Exercises
1. Apply the distribuve property to write equivalent expressions.
a. 7x + 7y
b. 15g + 20 h
c. 18m + 42n
d. 30a + 39b
e. 11f + 15f
f. 18h + 13h
g. 55m + 11
h. 7 + 56y

15. Module 4 Lesson 11 Factoring Expressions.notebook
15
March 26, 2014
2. Evaluate each of the expressions below.
a. 6x + 21y and 3(2x + 7y) x = 3 and y = 4
b. 5g + 7g and g(5 + 7) g = 6

16. Module 4 Lesson 11 Factoring Expressions.notebook
16
March 26, 2014
c. 14x + 2 and 2(7x + 1) x = 10
d. Explain any paerns that you noce in the results to parts (a)–(c).
e. What would happen if other values were given for the variables?

17. Module 4 Lesson 11 Factoring Expressions.notebook
17
March 26, 2014
Closing
Please take out your exit ticket for Lesson 11, close your
binder, and complete the exit ticket. This will be collected.
How can use you use your knowledge of GCF and the distribuve property to write equivalent expressions?
Find the missing value that makes the two expressions equivalent.
Explain how you determine the missing number.
I would expand each term and determine the greatest common factor. The greatest common
factor is the number that is placed on the blank line.

18. Module 4 Lesson 11 Factoring Expressions.notebook
18
March 26, 2014