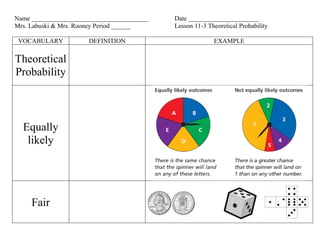
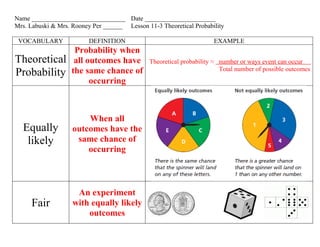
1. The document provides examples of calculating theoretical probabilities using a coin, dice, and other objects. It defines theoretical probability as the probability when all outcomes are equally likely. 2. It also discusses finding the probability of events not occurring by subtracting the probability of the event from 100%. 3. Several examples are worked out calculating probabilities of outcomes from coins, dice, spinners, bags of marbles using the formula for theoretical probability.

1. Name ____________________________________ Date ______________________
Mrs. Labuski & Mrs. Rooney Period ______ Lesson 11-3 Theoretical Probability
VOCABULARY DEFINITION EXAMPLE
Theoretical
Probability
Equally
likely
Fair

2. Finding Theoretical Probability
What is the probability that a fair coin will and heads up?
number or ways event can occur
P(heads) = Total number of possible outcomes
There are ________ outcomes: _______________ and _____________
number or ways event can occur
P(heads) = 2 possible outcomes
There is only one way for the coin to land heads up
1 way event can occur =
P(heads) = 2 possible outcomes
What is the probability of rolling a number less than 5 on a fair number cube?
number or ways event can occur
P(number less than 5) = Total number of possible outcomes
There are six outcomes: ____________________________
P(number less than 5) = number or ways event can occur
6 possible outcomes
There four ways to roll less than 5: ________________________
P(number less than 5) = 4 way event can occur =
6 possible outcomes
Finding the probabilities of Events Not Happening
To find the probability of an event not happening, find the probability that it will
happen and subtract from 100%.
Suppose there is a 10% chance that it will rain tonight. What is the probability that
it will not rain?
P(rain) + P(not rain)=100%
+ P(not rain)= 100%

3. Find the probability of each event using the spinner.
1. landing on blue ___________________
2. landing on red____________________
3. landing on green _________________
4. not landing on blue ________________
Find the probability of each event using the bag of marbles.
5. picking a black marble ________________
6. picking a striped marble ________________
7. picking a white marble ________________
8. not picking a white marble ________________
A standard number cube is rolled. Find each probability.
9. P(2) ________________ 10. P(even number) ________________
11. P(4 or 5) ________________ 12. P(odd number) ________________
13. Out of 10 fair coin tosses, a coin landed tails up 4 times. How does this
experimental probability of a fair coin landing tails up compare to the theoretical
probability of the same event?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
14. The probability of a spinner landing on blue is ¾. What is the probability of it
not landing on blue written as a percent?

4. A standard number cube is rolled. Find each probability
1. P(5) ________________ 2. P(1, 2, or 3) ________________
3. P(1 or 4) ________________ 4. P(negative number) ________________
5. P(even number) ____________ 6. P(odd number) ________________
7. P(positive number) ___________ 8. P(number less than 3) _______________
9. P(not 2) ________________ 10. P(not 3 or 4) ________________
Seven pieces of paper with the numbers 1, 2, 3, 4, 4, 5, and 6 printed on them
are placed in a bag. A student chooses one without looking. Compare the
probabilities. Write <, >, or = .
11. P(1) ______P(5) 12. P(2) ________P(4)
13. P(4 or 5) _______P(1 or 3) 14. P(less than 4) _______P(greater than 3)
15. Explain why this spinner could not be used for a fair experiment.
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
16. There is a 62% chance of rain tomorrow and a 19% chance of sleet. What is the
probability that neither event will occur?

5. Name _____________________________ Date ______________________
Mrs. Labuski & Mrs. Rooney Per ______ Lesson 11-3 Theoretical Probability
VOCABULARY DEFINITION EXAMPLE
Probability when
Theoretical all outcomes have Theoretical probability ≈ number or ways event can occur
the same chance of Total number of possible outcomes
Probability
occurring
When all
Equally outcomes have the
likely same chance of
occurring
An experiment
Fair with equally likely
outcomes

6. Finding Theoretical Probability
What is the probability that a fair coin will and heads up?
number or ways event can occur
P(heads) = Total number of possible outcomes
There are 2 outcomes: heads and tails
number or ways event can occur
P(heads) = 2 possible outcomes
There is only one way for the coin to land heads up
1 way event can occur = 1
P(heads) = 2 possible outcomes 2
What is the probability of rolling a number less than 5 on a fair number cube?
P(number less than 5) = number or ways event can occur
Total number of possible outcomes
There are six outcomes: 1,2,3,4,5,6
P(number less than 5) = number or ways event can occur
6 possible outcomes
There four ways to roll less than 5: 1,2,3,4
P(number less than 5) = 4 way event can occur = 4 = 2
6 possible outcomes 6 3
Finding the probabilities of Events Not Happening
To find the probability of an event not happening, find the probability that it will
happen and subtract from 100%.
Suppose there is a 10% chance that it will rain tonight. What is the probability that
it will not rain?
P(rain) + P(not rain)=100%
10% + P(not rain)= 100%
-10% -10%
P(not rain)= 90%

7. Find the probability of each event using the spinner.
1. landing on blue 3/5
2. landing on red 1/5
3. landing on green 1/5
4. not landing on blue 2/5
Find the probability of each event using the bag of marbles.
5. picking a black marble 4/9
6. picking a striped marble 1/3
7. picking a white marble 2/9
8. not picking a white marble 7/9
A standard number cube is rolled. Find each probability.
9. P(2) 1/6 10. P(even number) 3/6 = ½
11. P(4 or 5) 2/6 = 1/3 12. P(odd number) 3/6 = ½
13. Out of 10 fair coin tosses, a coin landed tails up 4 times. How does this
experimental probability of a fair coin landing tails up compare to the theoretical
probability of the same event?
experimental probability = 4/10 = 40% theoretical probability = ½ =50%
The experimental probability is 40%, which is less than the theoretical
probability which is 50%.
14. The probability of a spinner landing on blue is ¾. What is the probability of it
not landing on blue written as a percent? ¼ = 25%

8. A standard number cube is rolled. Find each probability
1. P(5) 1/6 2. P(1, 2, or 3) 3/6 = ½
3. P(1 or 4) 1/3_____________ 4. P(negative number) 0
5. P(even number) 3/6 = ½ ______ 6. P(odd number) 3/6 = ½
7. P(positive number) 1 or 100% 8. P(number less than 3) 1/3
9. P(not 2) 5/6 10. P(not 3 or 4) 4/6 = 2/3
Seven pieces of paper with the numbers 1, 2, 3, 4, 4, 5, and 6 printed on them
are placed in a bag. A student chooses one without looking. Compare the
probabilities. Write <, >, or = .
11. P(1) = P(5) 12. P(2) < P(4)
1 1 1 2
7 7 7 7
13. P(4 or 5) > P(1 or 3) 14. P(less than 4) > P(greater than 3)
3 2 3 4
7 7 7 7
15. Explain why this spinner could not be used for a fair experiment.
There is a greater chance of the spinner landing on red than on any other color
because there are two red sections and only one section of
every other color.
16. There is a 62% chance of rain tomorrow and a 19% chance of sleet. What is the
probability that neither event will occur?
62% 100%
+ 19% -81% 19%
81% 19%