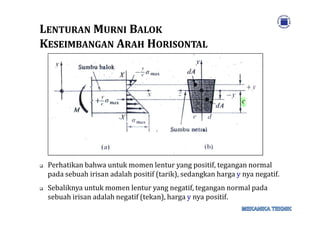
Dokumen tersebut membahas tentang distribusi tegangan dalam balok yang mengalami lenturan, dengan fokus pada konsep sumbu netral dan keseimbangan gaya serta momen pada balok. Diuraikan pula cara menghitung momen inersia untuk beberapa bentuk penampang balok sederhana.

1. LLENTURANENTURAN MMURNIURNI BBALOKALOK
MMOMENOMEN IINERSIANERSIAMMOMENOMEN IINERSIANERSIA

2. LLENTURANENTURAN MMURNIURNI BBALOKALOK
Dalam suatu irisan balok, tegangan normal yang dihasilkan oleh lenturan
berubah secara linier terhadap jaraknya dari sumbu netral.
Gambar (a), (b), (c) dan (d) menggambarkan hakekat dari distribusi
tegangan dalam suatu balok yang melawan momen lentur
Perubahan linier dari tegangan tersebut merupakan akibat dari
perubahan linier dalam regangan dan kesebandingan tegangan terhadap
regangan.

3. LLENTURANENTURAN MMURNIURNI BBALOKALOK
Berikut ini digambarkan sifat balok
pada saat melentur

4. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN AARAHRAH HHORISONTALORISONTAL
Suatu balok dengan lenturan murni seperti pada gambar di bawah ini,
haruslah berada dalam keseimbangan. Oleh karena itu, jumlah semua
gaya yang diambil dalam arah horisontal x haruslah nol, yaitu Σ Fx = 0.

5. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN AARAHRAH HHORISONTALORISONTAL
Perhatikan bahwa untuk momen lentur yang positif, tegangan normal
pada sebuah irisan adalah positif (tarik), sedangkan harga y nya negatif.
Sebaliknya untuk momen lentur yang negatif, tegangan normal pada
sebuah irisan adalah negatif (tekan), harga y nya positif.

6. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN AARAHRAH HHORISONTALORISONTAL
Sehingga diperoleh ungkapan –(y/c) σmax yang merupakan ungkapan
umum untuk setiap daerah kecil tak berhingga dA dari irisan balok pada
jarak y dari sumbu netral.

7. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN AARAHRAH HHORISONTALORISONTAL
Karena segmen pada balok tersebut hanya melawan sebuah kopel, maka
jumlah (integral) dari semua gaya yang bekerja pada irisan balok tersebut
haruslah nol. Sehingga Σ Fx = 0 adalah
−σmax/c konstan

8. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN AARAHRAH HHORISONTALORISONTAL
Pada gambar, karena balok mendapatkan tegangan maka nilai variabel σmax , c dan
dA tidak mungkin bernilai nol. Sehingga hanya ada kemungkinan satu variabel
yang dapat bernilai nol, agar dapat dihasilkan Σ Fx = 0.
Variabel tersebut adalah y, yang merupakan jarak sebuah titik berat luas dA dari
sumbu netral. Dengan kata lain sumbu netral haruslah melalui titik berat dari
daerah penampang balok.
Jadi, sumbu netral dapat ditentukan dengan mudah untuk setiap balok, yaitu
dengan mencari titik berat dari daerah irisan penampang balok tersebut.

9. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN MMOMENOMEN
Tinggal satu lagi persamaan keseimbangan statis penting yang akan
digunakan pada segmen balok pada gambar di atas. Persamaan ini adalah
Σ Mz = 0.
Momen luar M mendapatkan perlawanan yang besarnya sama dengan
momen lentur dalam yang dibentuk oleh tegangan lentur pada suatu
irisan.

10. LLENTURANENTURAN MMURNIURNI BBALOKALOK
KKESEIMBANGANESEIMBANGAN MMOMENOMEN
Besaran terakhir ini ditentukan dengan menjumlahkan gaya-gaya pada
daerah kecil tak berhingga dA, dikalikan dengan lengan yang
bersangkutan terhadap sumbu netral.
Momen inersia

11. LLENTURANENTURAN MMURNIURNI BBALOKALOK
PPERHITUNGANERHITUNGAN MMOMENOMEN IINERSIANERSIA
Integral y2 dA bergantung pada sifat geometris dari irisan penampang.
Dalam mekanika bahan integral ini dinamakan sebagai momen inersia.
Momen inersia (I) adalah suatu tetapan untuk luasan tertentu dari
penampang terhadap sumbu titik beratnya (bila jarak y diukur dari
sumbu titk berat, momen inersia Integral y2 dA).
Dengan menggunakan notasi hubungan persamaan dapat ditulis menjadiDengan menggunakan notasi hubungan persamaan dapat ditulis menjadi
Atau untuk setiap tegangan pada titik penampang
I
Mc
atauI
c
M −=−= max
max
σ
σ
∫=
−=
A
dAyIana
I
My
2
:dim
σ

12. LLENTURANENTURAN MMURNIURNI BBALOKALOK
PPERHITUNGANERHITUNGAN MMOMENOMEN IINERSIANERSIA
Langkah pertama untuk mengevaluasi momen inersia I untuk suatu
daerah adalah mendapatkan titik berat dari daerah tersebut.
Untuk mendapatkan momen inersia dari beberapa bentuk sederhana
digunakan teorema sumbu sejajar
2
0 AdIIzz += 0zz

13. LLENTURANENTURAN MMURNIURNI BBALOKALOK
CCONTOHONTOH 11
Hitunglah momen inersia terhadap sumbu horizontal yang melalui titik
berat luas penampang persegi yang terlihat dalam gambar

14. LLENTURANENTURAN MMURNIURNI BBALOKALOK
PPENYELESAIANENYELESAIAN 11
Titik berat irisan ini terletak pada perpotongan
kedua sumbu simetri dari luas siku empat.
Karena itu lebih baik menulis dA dengan d by.
Jadi
Dengan cara yang sama diperoleh
Bentuk-bentuk ini sangat sering dipakai, karena balok sikuempat sangat
banyak digunakan dalam praktek.
12
3
hb
Iyy =
12
3
0
bh
IIzz ==

15. LLENTURANENTURAN MMURNIURNI BBALOKALOK
CCONTOHONTOH 22
Tentukanlah momen inersia I terhadap sumbu horisontal untuk luas yang
terlihat dalam gambar di bawah ini

16. LLENTURANENTURAN MMURNIURNI BBALOKALOK
PPENYELESAIANENYELESAIAN 22