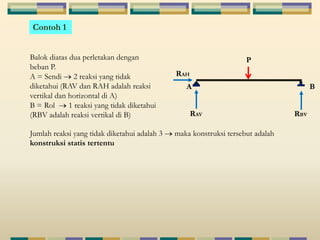
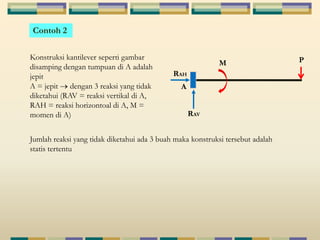
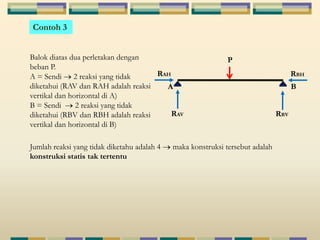
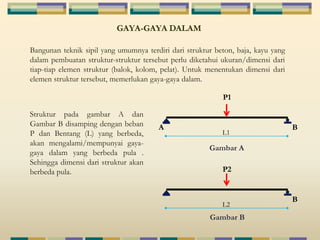
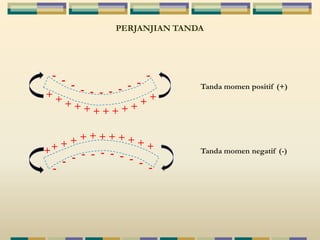
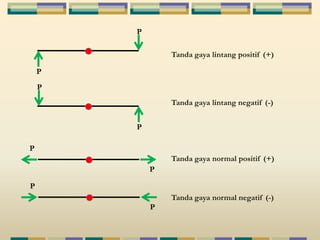
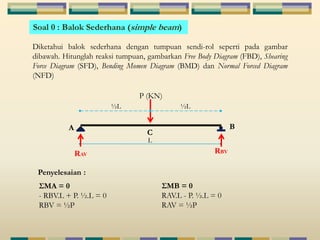
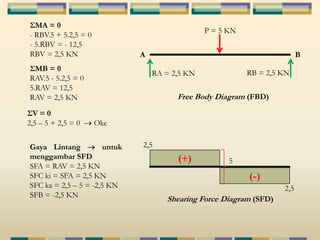
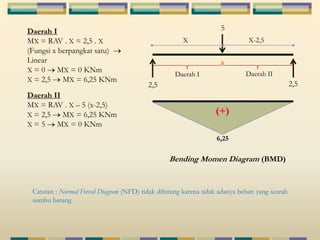
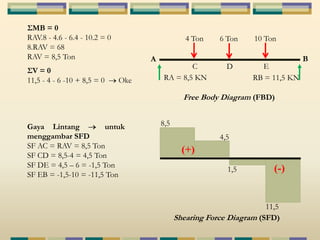
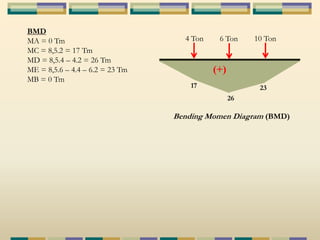
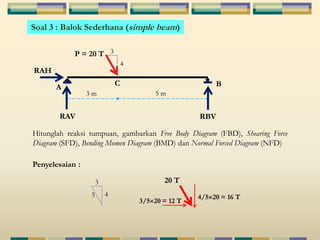
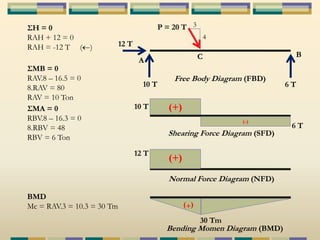
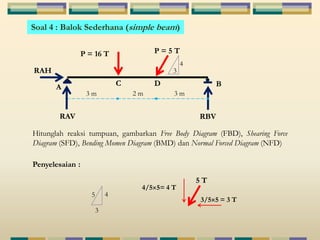
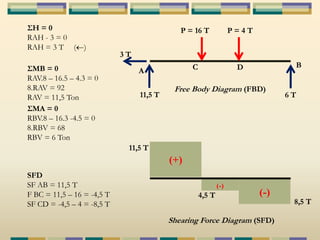
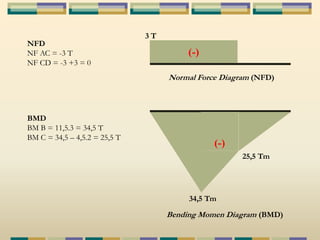
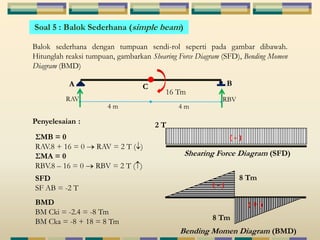
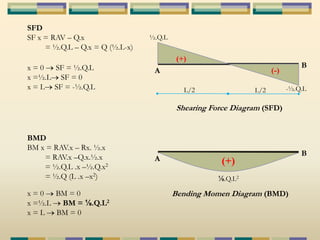
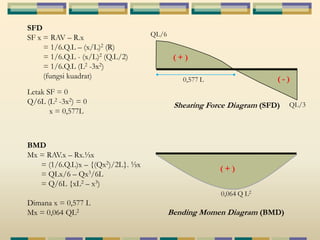
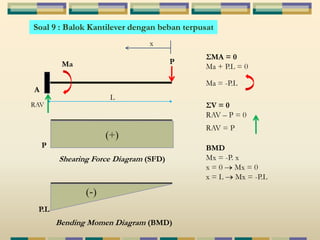
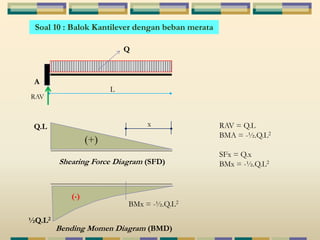
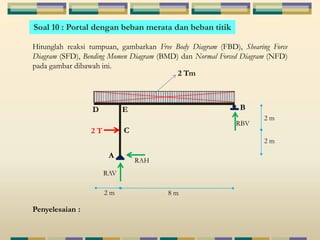
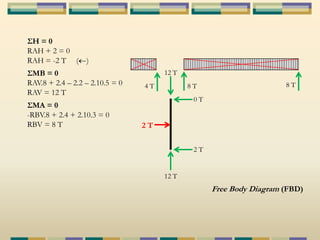
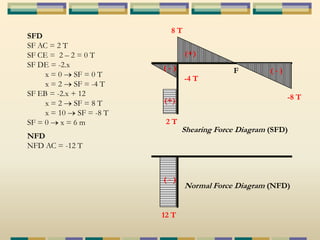
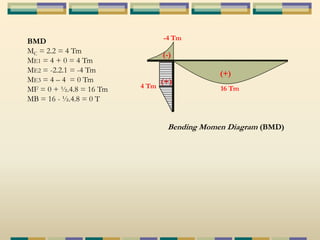
Dokumen tersebut membahas tentang struktur statis tertentu pada mekanika struktur, dimana struktur tersebut dapat diselesaikan menggunakan persamaan keseimbangan berupa jumlah gaya horizontal, vertikal dan momen yang sama dengan nol. Contoh struktur statis tertentu adalah balok diatas dua perletakan dengan jumlah reaksi yang tidak diketahui maksimal tiga. Dokumen juga menjelaskan tentang gaya-gaya dalam sepert