This document summarizes key concepts from a lecture on numerical analysis, including:
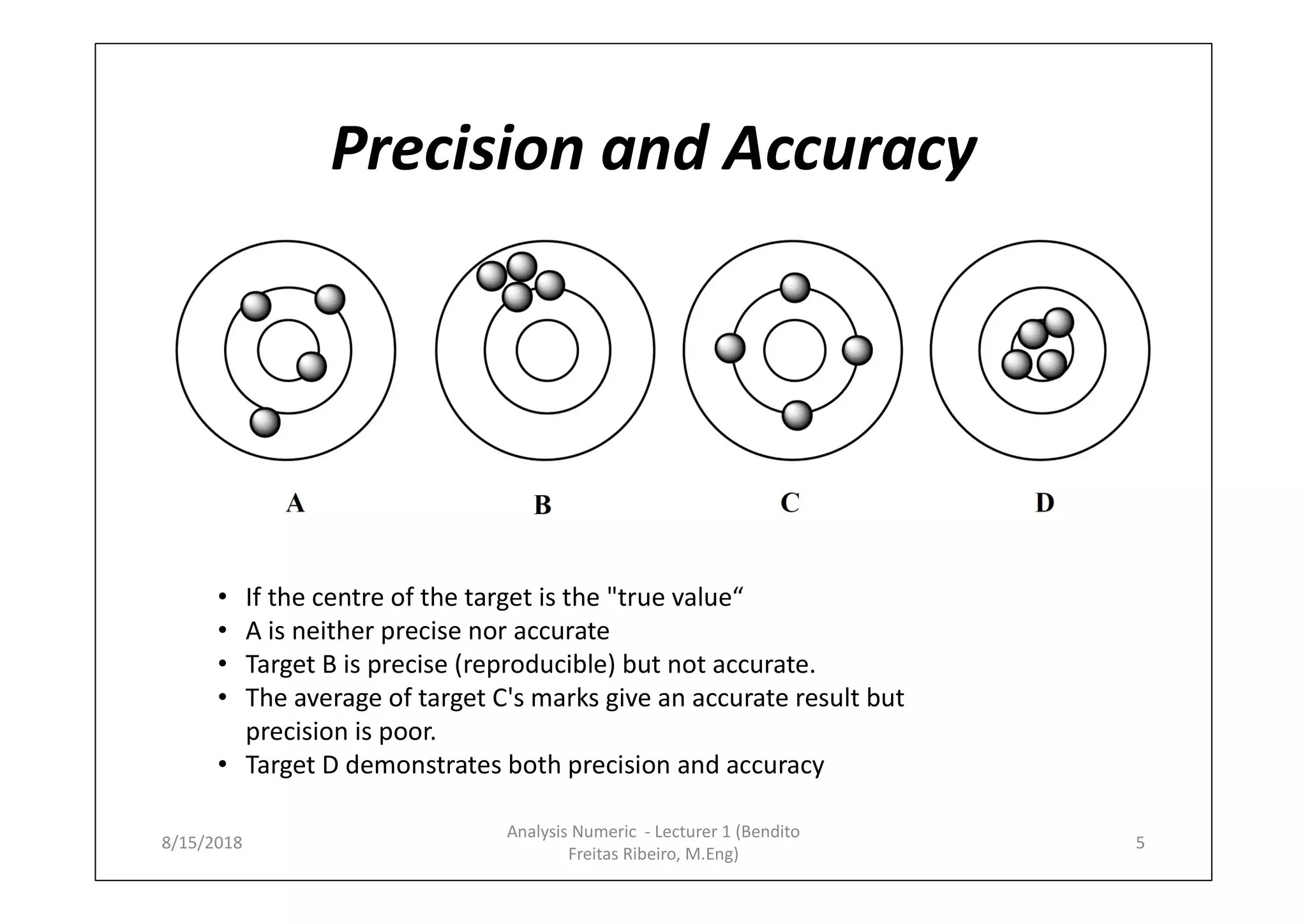
- Definitions of precision, accuracy, and different types of errors like random, systematic, and gross errors.
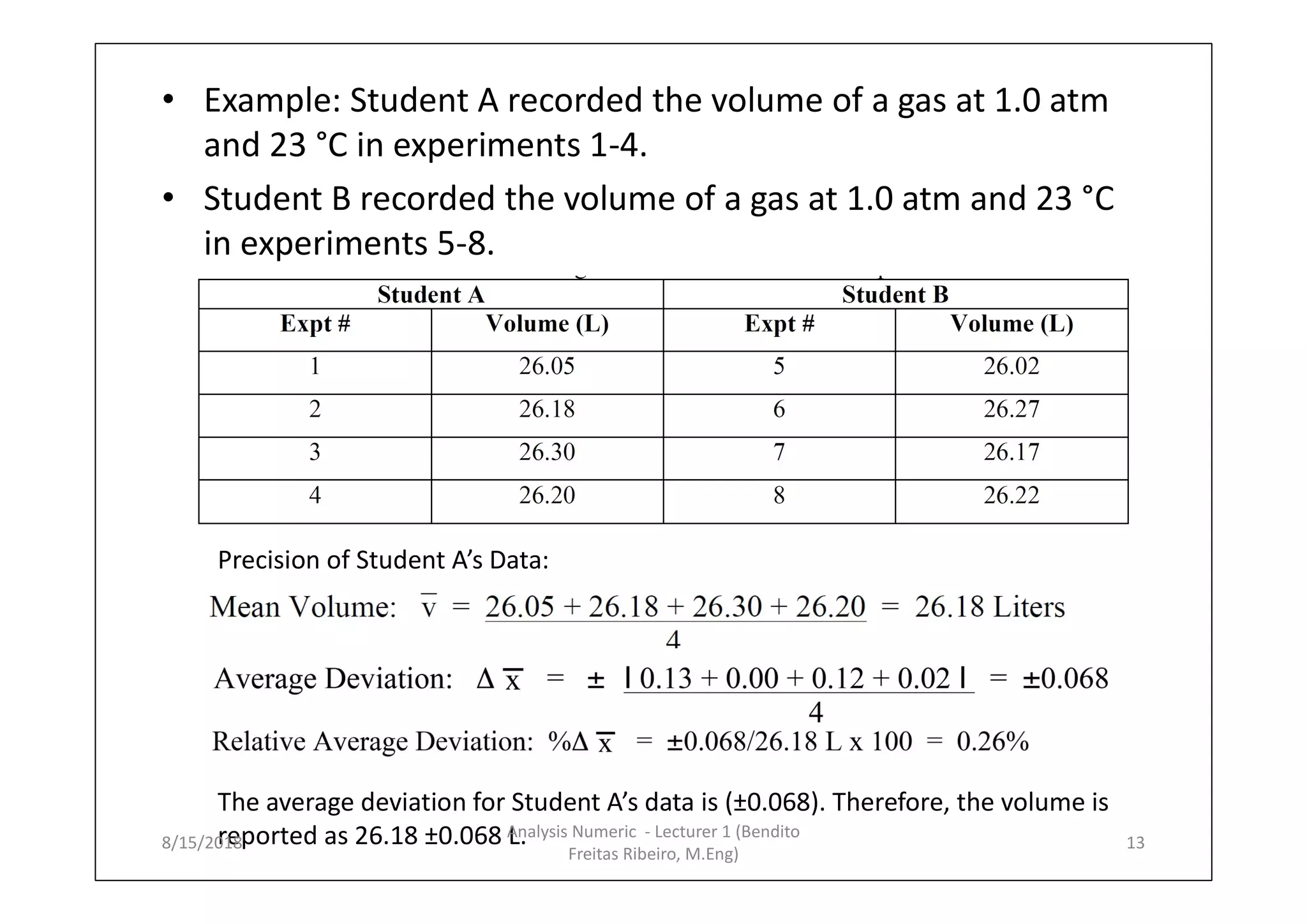
- How to calculate average deviation, standard deviation, and percent error to quantify precision and accuracy.
- Formulas and examples for propagating error in mathematical operations like addition, subtraction, multiplication and division.
- An example error propagation exercise calculating the standard deviation of a sum of measurements.