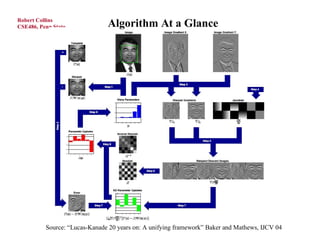
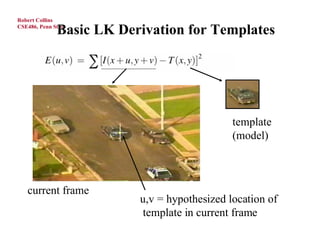
The document discusses the Lucas-Kanade template tracking method. It begins with a review of Lucas-Kanade optical flow, then describes how the same approach can be used to track larger image patches or templates by imposing the constraint that neighboring pixels have similar motion. It presents the derivation step-by-step, showing how a Taylor series approximation allows formulation as a least squares problem. An example Jacobian for affine motion models is provided. The algorithm iterates between warping the template, computing error, estimating motion parameters, and updating. State-of-the-art examples include tracking facial mesh models.

1. Robert Collins
CSE486, Penn State
Lecture 30:
Video Tracking: Lucas-Kanade

2. Robert Collins
CSE486, Penn State
Two Popular Tracking Methods
• Mean-shift color histogram tracking (last time)
• Lucas-Kanade template tracking (today)

3. Robert Collins
CSE486, Penn State
Lucas-Kanade Tracking

4. Robert Collins
CSE486, Penn State Review: Lucas-Kanade
• Brightness constancy
• One equation two unknowns
unknown flow vector
temporal gradient spatial gradient
• How to get more equations for a pixel?
– Basic idea: impose additional constraints
• one method: pretend the pixel’s neighbors have the same (u,v)
– If we use a 5x5 window, that gives us 25 equations per pixel!
* From Khurram Hassan-Shafique CAP5415 Computer Vision 2003

5. Robert Collins
CSE486, Penn State
Review: Lucas-Kanade (cont)
• Now we have more equations than unknowns
• Solution: solve least squares problem
– minimum least squares solution given by solution (in d) of:
– The summations are over all pixels in the K x K window
– This technique was first proposed by Lucas & Kanade (1981)
• described in Trucco & Verri reading
* From Khurram Hassan-Shafique CAP5415 Computer Vision 2003

6. Robert Collins
CSE486, Penn State
Lucas Kanade Tracking
Traditional Lucas-Kanade is typically run on small,
corner-like features (e.g. 5x5) to compute optic flow.
Observation: There’s no reason we can’t use the same
approach on a larger window around the object being
tracked.
80x50 pixels

7. Robert Collins
Basic LK Derivation for Templates
CSE486, Penn State
template
(model)
current frame
u,v = hypothesized location of
template in current frame

8. Robert Collins
Basic LK Derivation for Templates
CSE486, Penn State
First order approx
Take partial derivs and set to zero
Form matrix equation
solve via
least-squares

9. Robert Collins
CSE486, Penn State
One Problem with this...
Assumption of constant flow (pure translation) for
all pixels in a larger window is unreasonable for
long periods of time.
However, we can easily generalize Lucas-Kanade
approach to other 2D parametric motion models
(like affine or projective) by introducing a “warp”
function W.
generalize
x
 [ I (W ([ x, y ]; P))  T ([ x, y ])]2
  within image patch
 y
 

10. Robert Collins
CSE486, Penn State
Step-by-Step Derivation
The key to the derivation is Taylor series approximation:
W
[ I (W ([ x, y ]; P  P)) ~ [ I (W ([ x, y ]; P))  I
~ P
P
We will derive this step-by-step. First, we need two background formula:

11. Robert Collins
CSE486, Penn State
Step-by-Step Derivation
First consider the expansion for a single variable p

12. Robert Collins
CSE486, Penn State
Step-by-Step Derivation
Note that each variable parameter pi contributes a term of the form

13. Robert Collins
CSE486, Penn State
Step-by-Step Derivation
Now let’s rewrite the expression as a matrix equation. For each term,
we can rewrite:
So that we have:

14. Robert Collins
CSE486, Penn State
Step-by-Step Derivation
Further collecting the dw/dpi terms into a matrix, we can write:
which are the terms in the matrix equation:
~ W
[ I (W ([ x, y ]; P  P)) ~ [ I (W ([ x, y ]; P))  I P
P

15. Robert Collins
Example: Jacobian of Affine Warp
CSE486, Penn State
Let W([x, y]; P)  [Wx , Wy ]
general equation of Jacobian  Wx Wx Wx Wx 

W  P P P P 
 1 2 3 n

P Wy Wy Wy Wy 

 P
 1 P2 P3 P 
n 
affine warp function (6 parameters)
 x  xP  yP3  P5 
1

 x W xP2  y  yP4  P6 
1  p1
W ([ x, y ]; P )  
p3 p5   
 y    
 p6    P P
 p2 1  p4  1
   x 0 y 0 1 0
 
 0 x 0 y 0 1 

16. Source: “Lucas-Kanade 20 years on: A unifying framework” Baker and Mathews, IJCV 04
Robert Collins
CSE486, Penn State
Iterate Warp I to obtain I(W([x y];P))
Compute the error image T(x) – I(W([x y]; P))
Warp the gradient I with W([x y]; P)
W
Evaluate at ([x y]; P) (Jacobian)
P
W
Compute steepest descent images I
P
W T W
Compute Hessian matrix  (I P
) (I
P
)
W T
Compute  ( I P
) (T ( x, y )  I (W ([ x, y ]; P )))
Compute P
Update P P + P
Until P magnitude is negligible
Dr. Ng Teck Khim

17. Robert Collins
CSE486, Penn State Algorithm At a Glance
Source: “Lucas-Kanade 20 years on: A unifying framework” Baker and Mathews, IJCV 04

18. Robert Collins
State of the Art Lucas Kanade Tracking
CSE486, Penn State
Tracking facial mesh models (piecewise affine)
QuickTime™ and a
YUV420 codec decompressor
are needed to see this picture.
Baker, Matthews, CMU