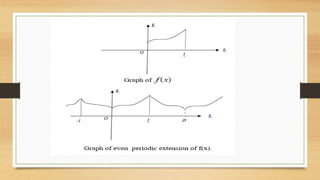
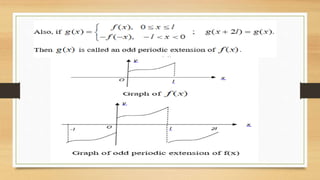
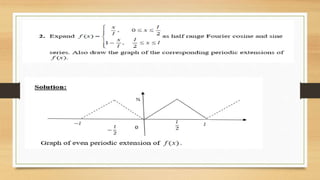
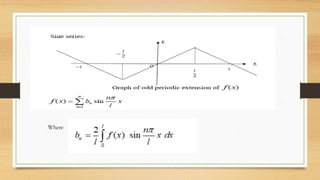
The document discusses half-range Fourier series expansions for functions defined over a finite range. It explains that such expansions are possible if the functions can be extended to periodic even or odd functions. Specifically, a piecewise continuous function defined over a finite interval can be extended to a periodic function that is either even or odd, allowing it to be represented by a half-range cosine or sine series expansion through harmonic analysis.

1. HALF-RANGE FOURIER SERIES
 Half-Range cosine series
 Half-Range sine series
 Harmonic analysis

2. Half range Expansions
 While solving various physical and engineering problems, there is a practical need for expanding functions defined
over a finite range. Such an expansion is possible if functions under consideration can be extended to a periodic
function which is either even or odd.
 Consider a piecewise continuous function defined in a finite interval . Then it is possible to extend to a
periodic function, which is even or odd.
)
(x
f )
,
0
( l )
(x
f

10. Where