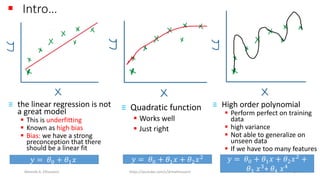
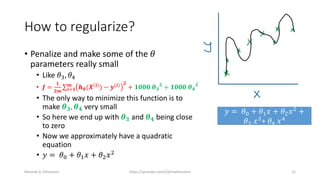
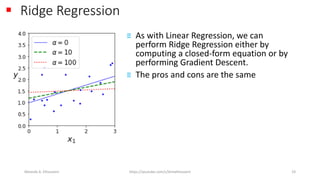
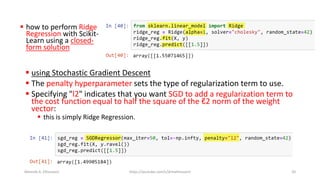
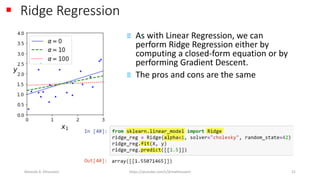
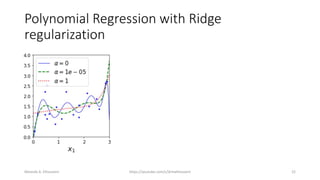
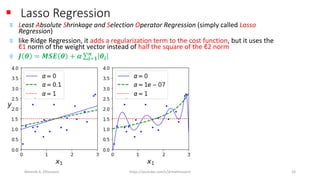
The document discusses the concepts of overfitting and underfitting in machine learning models, highlighting how regularization can mitigate these issues by adjusting model complexity through techniques such as ridge regression, lasso regression, and elastic net. It emphasizes the importance of choosing the right model and regularization parameters to improve generalization without sacrificing performance on unseen data. Additionally, it introduces early stopping as a practical regularization method during model training to avoid overfitting.