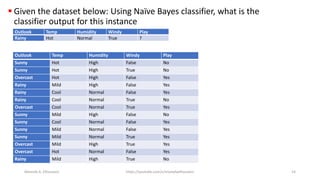
The document discusses the Naïve Bayes classifier, including its application to diagnosing diseases using Bayes' theorem. It provides examples of the theorem in practice, particularly in the context of a disease with a low incidence rate and a test with false positives. Additionally, it covers handling text and categorical data in machine learning, and includes a focus on the Pima Indian diabetes dataset for predictive modeling.