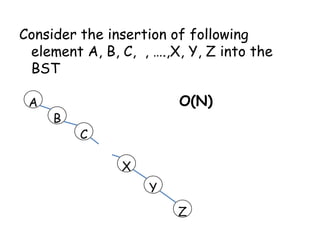
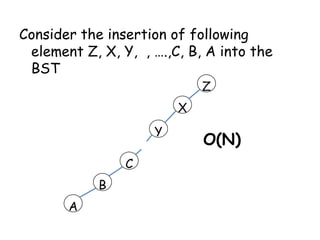
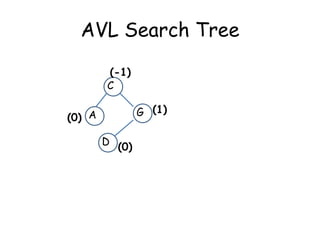
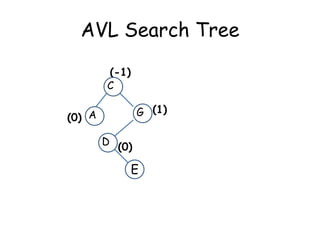
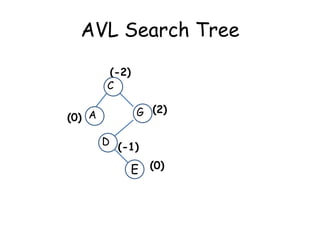
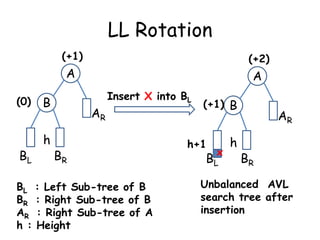
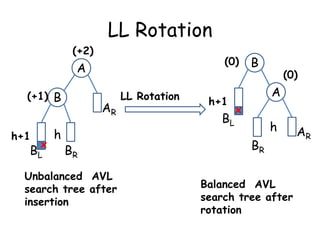
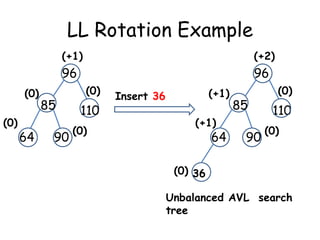
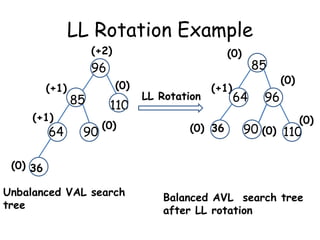
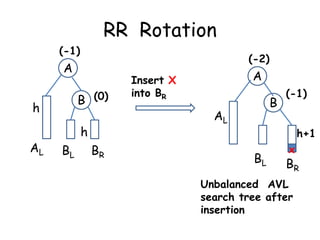
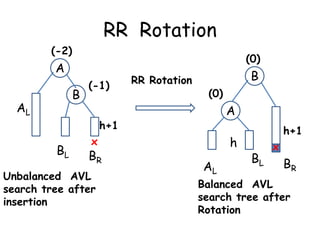
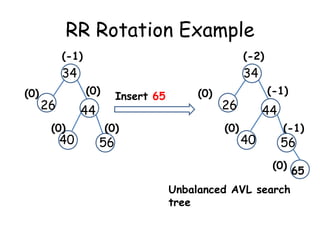
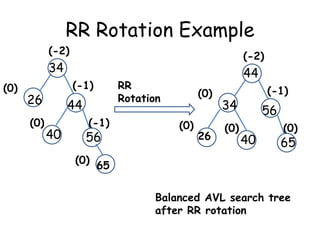
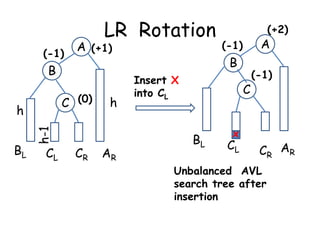
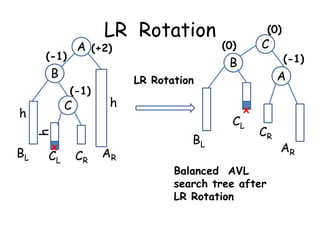
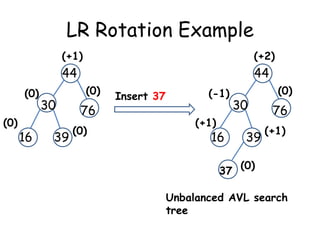
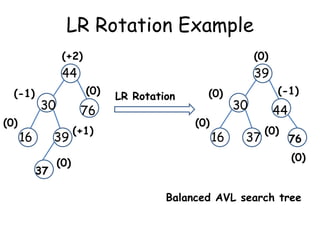
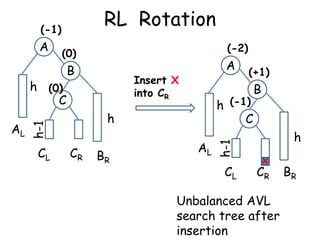
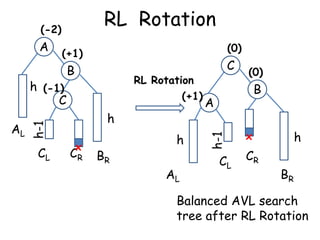
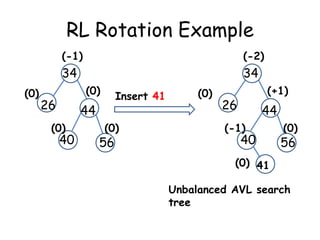
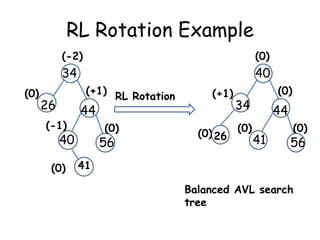
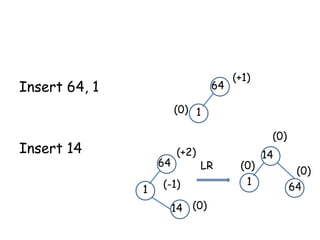
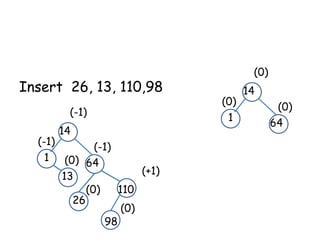
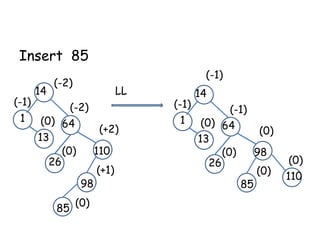
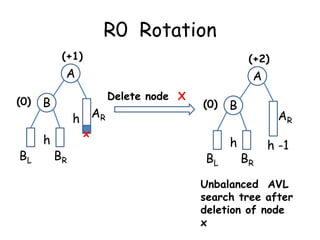
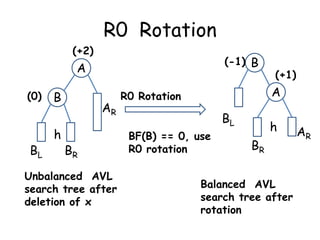
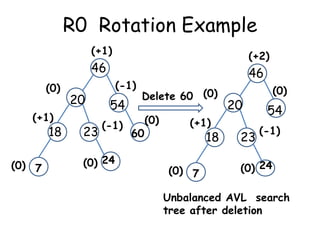
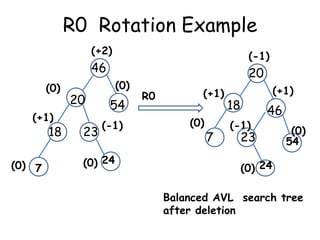
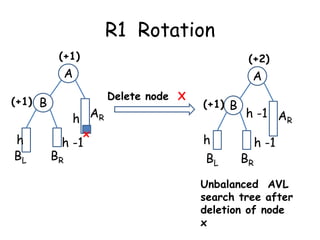
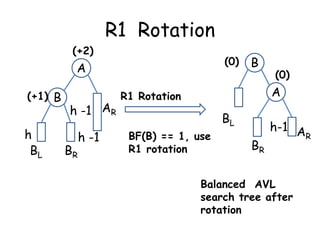
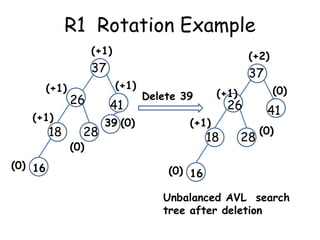
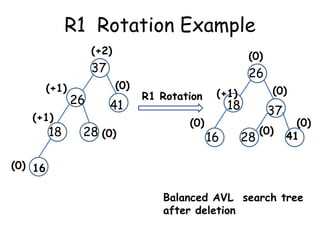
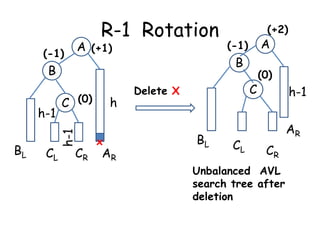
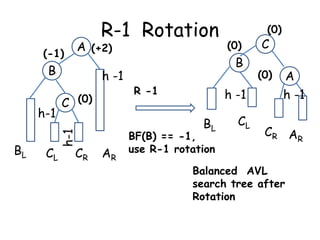
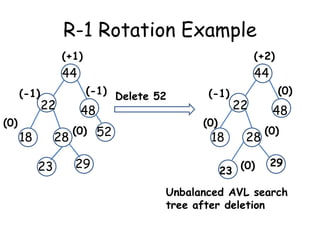
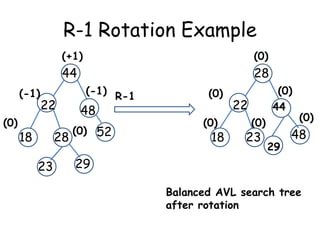
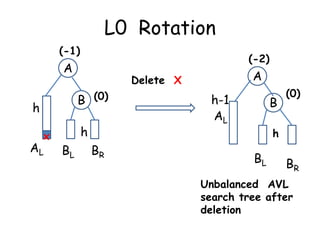
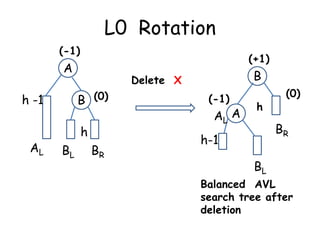
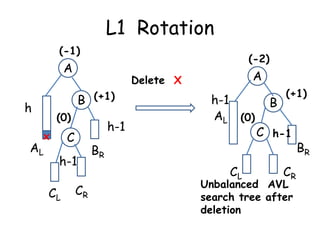
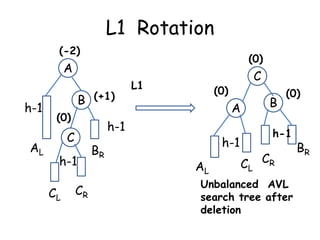
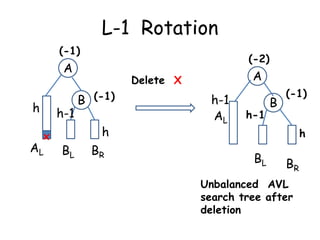
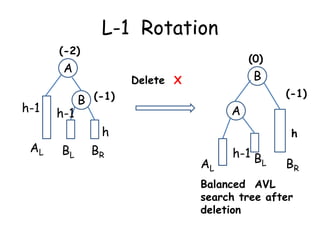
This document discusses balanced binary search trees (BSTs), specifically AVL trees. It explains that AVL trees ensure insertions and deletions are O(log N) by keeping the height difference between left and right subtrees no more than 1. It covers the four types of rotations (LL, RR, LR, RL) used to rebalance the tree after insertions or deletions. Deletions can also cause imbalance and require L, R, L0, L1, R0, R1, L-1, R-1 rotations depending on the balancing factors. Examples are provided for each type of rotation.

1. Data Structure and
Algorithm (CS-102)
Ashok K Turuk

2. Consider the insertion of following
element A, B, C, , ….,X, Y, Z into the
BST
A
B
O(N)
C
X
Y
Z

3. Consider the insertion of following
element Z, X, Y, , ….,C, B, A into the
BST
Z
X
Y
C
B
A
O(N)

4. Balanced binary tree
• The disadvantage of a binary search tree is that its
height can be as large as N-1
• This means that the time needed to perform insertion
and deletion and many other operations can be O(N)
in the worst case
• We want a tree with small height
• A binary tree with N node has height at least
(log
N)
• Thus, our goal is to keep the height of a binary search
tree O(log N)
• Such trees are called balanced binary search trees.
Examples are AVL tree, red-black tree.

5. AVL tree
Height of a node
• The height of a leaf is 1. The height of
a null pointer is zero.
• The height of an internal node is the
maximum height of its children plus 1

6. AVL tree
• An AVL tree is a binary search tree in
which
– for every node in the tree, the height of
the left and right subtrees differ by at
most 1.
– An empty binary tree is an AVL tree

7. AVL tree
TL left subtree of T
h(TL ) Height of the subtree TL
TR Right subtree of T
h(TR ) Height of the subtree TR
T is an AVL tree iff TL and TR are AVL
tree and |h(TL ) - h(TR ) | <= 1
h(TL ) - h(TR ) is known as balancing factor
(BF) and for an AVL tree the BF of a
node can be either 0 , 1, or -1

8. AVL Search Tree
(-1)
C
G (1)
(0) A
D (0)

9. Insertion in AVL search Tree
Insertion into an AVL search tree may
affect the BF of a node, resulting the
BST unbalanced.
A technique called Rotation is used to
restore he balance of the search tree

10. AVL Search Tree
(-1)
C
G (1)
(0) A
D (0)
E

11. AVL Search Tree
(-2)
C
(0) A
G (2)
D (-1)
E (0)

12. Rotation
To perform rotation – Identify a specific
node A whose BF(A) is neither 0, 1, or -1
and which is the nearest ancestor to
the inserted node on the path from the
inserted node to the root

13. Rotation
Rebalancing rotation are classified as LL,
LR, RR and RL
LL Rotation: Inserted node is in the left
sub-tree of left sub-tree of node A
RR Rotation: Inserted node is in the right
sub-tree of right sub-tree of node A
LR Rotation: Inserted node is in the right
sub-tree of left sub-tree of node A
RL Rotation: Inserted node is in the left
sub-tree of right sub-tree of node A

14. LL Rotation
(+1)
(+2)
A
(0)
BL
B
h
A
AR
Insert X into BL
c
BR
BL : Left Sub-tree of B
BR : Right Sub-tree of B
AR : Right Sub-tree of A
h : Height
(+1) B
h+1
x
BL
h
AR
c
BR
Unbalanced AVL
search tree after
insertion

15. LL Rotation
(+2)
(0)
A
(+1) B
h+1
x
BL
h
AR
c
BR
Unbalanced AVL
search tree after
insertion
LL Rotation
h+1
BL
B
(0)
A
x
c
h
BR
Balanced AVL
search tree after
rotation
AR

16. LL Rotation Example
(+1)
96
(0)
(0)
64
(+2)
96
85
90
(0)
110
(0)
(+1)
Insert 36
(+1)
64
85
90
(0)
110
(0)
(0) 36
Unbalanced AVL search
tree

17. LL Rotation Example
(+2)
(0)
96
(+1)
(+1)
64
85
90
(0)
110
(0)
LL Rotation
(+1)
(0) 36
85
64
(0)
96
(0)
90 (0) 110
(0) 36
Unbalanced VAL search
tree
Balanced AVL search tree
after LL rotation

18. RR Rotation
(-1)
(-2)
A
B (0)
h
AL
h
BL
c
BR
A
Insert X
into BR
B
AL
(-1)
c
BL
x
h+1
BR
Unbalanced AVL
search tree after
insertion

19. RR Rotation
(-2)
(0)
A
B
AL
(-1)
c
BL
RR Rotation
B
(0)
A
h+1
c
h
x
BR
Unbalanced AVL
search tree after
insertion
AL
BL
h+1
x
BR
Balanced AVL
search tree after
Rotation

20. RR Rotation Example
(-1)
34
(0)
(-2)
34
(0)
26
Insert 65
44
(0)
40
(0)
56
(0)
(-1)
26
(0)
44
40
(-1)
56
(0) 65
Unbalanced AVL search
tree

21. RR Rotation Example
(-2)
(-2)
34
(0)
(-1)
26
(0)
44
40
(-1)
56
44
RR
Rotation
(0)
(0)
26
(-1)
34
(0)
56
40
(0)
65
(0) 65
Balanced AVL search tree
after RR rotation

22. LR Rotation
(-1)
A (+1)
B
C (0)
h
h
c
BL
CL
CR
AR
(+2)
A
(-1)
B
Insert X
into CL
C
BL
x
CL
(-1)
c
CR AR
Unbalanced AVL
search tree after
insertion

23. LR Rotation
A (+2)
(-1)
B
(-1)
C
h
BL
x
CL
C
(0)
B
h
AR
x
BL
(-1)
A
LR Rotation
c
CR
(0)
CL
c
CR
Balanced AVL
search tree after
LR Rotation
AR

24. LR Rotation Example
(+1)
44
(0)
(0)
16
(+2)
44
30
39
(0)
76
(0)
Insert 37
(-1)
(+1)
16
30
39
(0)
76
(+1)
37 (0)
Unbalanced AVL search
tree

25. LR Rotation Example
(+2)
44
(-1)
(0)
(0)
39
(0)
30
16
76
39
37
(0)
(+1)
LR Rotation
(0)
(0)
16
30
37
(-1)
44
(0)
76
(0)
Balanced AVL search tree

26. RL Rotation
(-1)
A
h (0)
C
AL
(-2)
(0)
B
Insert X
into CR
c
CL
A
CR
h (-1)
C
h
BR
(+1)
AL
B
c
CL
x
CR
Unbalanced AVL
search tree after
insertion
h
BR

27. RL Rotation
(-2)
A
h (-1)
C
AL
B
RL Rotation
(+1)
c
CL
(0)
(+1)
x
CR
h
BR
C
(0)
B
A
c
AL
h
x
h
CL
CR
BR
Balanced AVL search
tree after RL Rotation

28. RL Rotation Example
(-1)
34
(0)
(-2)
34
(0)
26
Insert 41
44
(0)
40
(0)
56
(0)
(+1)
26
44
(-1)
40
(0)
56
(0) 41
Unbalanced AVL search
tree

29. RL Rotation Example
(-2)
34
(0)
(0)
40
(+1) RL Rotation
26
(-1)
44
(0)
40
(0)
56
(+1)
(0)
34
(0) 26 (0)
44
41
(0)
56
41
Balanced AVL search
tree

30. AVL Tree
Construct an AVL search tree by inserting
the following elements in the order of
their occurrence
64, 1, 14, 26, 13, 110, 98, 85

31. Insert 64, 1
64
(+1)
(0) 1
(0)
Insert 14
64
1
(+2)
LR
(-1)
14 (0)
(0)
1
14
(0)
64

32. Insert 26, 13, 110,98
(-1)
14
(-1)
(-1)
1 (0) 64
(+1)
13
(0)
110
26
(0)
98
(0)
(0)
1
14
(0)
64

33. Insert 85
(-1)
1
14
(-1)
(-2)
LL
(-2)
(0) 64
13
(0)
26
(+2)
110
98
85 (0)
(+1)
14
(-1)
(-1)
1 (0) 64
(0)
13
(0)
98
26
(0)
85
(0)
110

34. Deletion in AVL search Tree
Deletion in AVL search tree proceed the
same way as the deletion in binary
search tree
However, in the event of imbalance due to
deletion, one or more rotation need to
be applied to balance the AVL tree.

35. AVL deletion
Let A be the closest ancestor node on the
path from X (deleted node) to the root
with a balancing factor +2 or -2
Classify the rotation as L or R depending
on whether the deletion occurred on the
left or right subtree of A

36. AVL Deletion
Depending on the value of BF(B) where B
is the root of the left or right subtree
of A, the R or L imbalance is further
classified as R0, R1 and R -1 or L0, L1
and L-1.

37. R0 Rotation
(+1)
(+2)
A
(0)
BL
Delete node X
B
h
A
h AR
c
BR
(0)
x
BL
B
h
AR
c
BR
h -1
Unbalanced AVL
search tree after
deletion of node
x

38. R0 Rotation
(+2)
(-1) B
A
(0)
BL
B
h
AR
c
BR
Unbalanced AVL
search tree after
deletion of x
(+1)
A
R0 Rotation
BF(B) == 0, use
R0 rotation
BL
c
h
BR
Balanced AVL
search tree after
rotation
AR

39. R0 Rotation Example
(+1)
(+2)
46
(0)
(+1)
18
(0) 7
20
23
(-1)
54
(-1)
(0) 24
46
Delete 60 (0)
60
(0)
(+1)
18
(0) 7
20
23
(0)
54
(-1)
(0) 24
Unbalanced AVL search
tree after deletion

40. R0 Rotation Example
(+2)
(-1)
46
(0)
(+1)
18
(0) 7
20
23
(0)
54
(-1)
(0) 24
20
R0
(+1)
(0)
7
(+1)
18
(-1)
46
23
(0)
54
(0) 24
Balanced AVL search tree
after deletion

41. R1 Rotation
(+1)
(+2)
A
Delete node X
(+1) B
h
BL
A
h AR
c
x
h -1
BR
(+1) B
h
BL
h -1 AR
c
BR
h -1
Unbalanced AVL
search tree after
deletion of node
x

42. R1 Rotation
(+2)
(0)
A
(+1) B
h
BL
h -1 AR
c
BR
h -1
B
(0)
A
R1 Rotation
BF(B) == 1, use
R1 rotation
BL
c
BR
h-1 A
R
Balanced AVL
search tree after
rotation

43. R1 Rotation Example
(+1)
(+2)
37
(+1)
(+1)
18
(0) 16
26
28
(+1)
41
39 (0)
37
(+1)
Delete 39
26
(+1)
18
(0)
28
(0)
41
(0)
(0) 16
Unbalanced AVL search
tree after deletion

44. R1 Rotation Example
(+2)
(0)
37
(+1)
(+1)
18
26
(0)
41
28 (0)
26
R1 Rotation
(0)
(0)
(+1)
18
16
37
28
(0)
(0)
41
(0) 16
Balanced AVL search tree
after deletion

45. R-1 Rotation
(-1)
A (+1)
h-1
c
BL
CL
CR
h
A
(-1)
B
B
C (0)
(+2)
C
Delete X
(0)
h-1
c
x
AR
BL
CL
CR
Unbalanced AVL
search tree after
deletion
AR

46. R-1 Rotation
(-1)
A (+2)
B
h-1
h -1
C (0)
BL
CL
CR
AR
(0)
B
R -1
h -1
BL
c
(0)
BF(B) == -1,
use R-1 rotation
CL
C
(0)
c
A
h -1
CR AR
Balanced AVL
search tree after
Rotation

47. R-1 Rotation Example
(+1)
44
(-1)
(0)
22
(+2)
44
(-1) Delete 52
48
(0) 52
28
18
23
29
(-1)
(0)
18
22
28
23 (0)
(0)
48
(0)
29
Unbalanced AVL search
tree after deletion

48. R-1 Rotation Example
(+1)
44
(-1)
(0)
22
(0)
28
(-1) R-1
48
(0) 52
28
18
23
(0)
(0)
18
(0)
44
22
(0)
23
29
(0)
48
29
Balanced AVL search tree
after rotation

49. L0 Rotation
(-1)
(-2)
A
B (0)
h
x
AL
h
BL
A
Delete X
c
BR
h-1
AL
B
h
BL
(0)
c
BR
Unbalanced AVL
search tree after
deletion

50. L0 Rotation
(-1)
(+1)
A
B (0)
h -1
AL
h
BL
B
Delete X
c
BR
(-1)
AL A
h
c
(0)
BR
h-1
BL
Balanced AVL
search tree after
deletion

51. L1 Rotation
(-1)
(-2)
A
B (+1)
h
(0)
AL
c
C
x
h-1
CL
A
Delete X
CR
h-1
h-1
AL (0)
B
(+1)
C h-1c
BR
CL
CR
Unbalanced AVL
search tree after
deletion
BR

52. L1 Rotation
(-2)
(0)
A
h-1
AL
B (+1)
(0)
c
C
h-1
CL
CR
BR
L1
C
(0)
A
h-1
h-1
AL
B
(0)
h-1c
CL CR
Unbalanced AVL
search tree after
deletion
BR

53. L-1 Rotation
(-1)
(-2)
A
h
h-1
x
AL
B (-1)
c
BL
A
Delete X
h
BR
h-1
AL
h-1
B
(-1)
c
BL
BR
Unbalanced AVL
search tree after
deletion
h

54. L-1 Rotation
(-2)
(0)
A
h-1
h-1
BL
(-1)
B (-1)
c
AL
B
Delete X
A
h
BR
c
AL
h-1 B
L
h
BR
Balanced AVL
search tree after
deletion