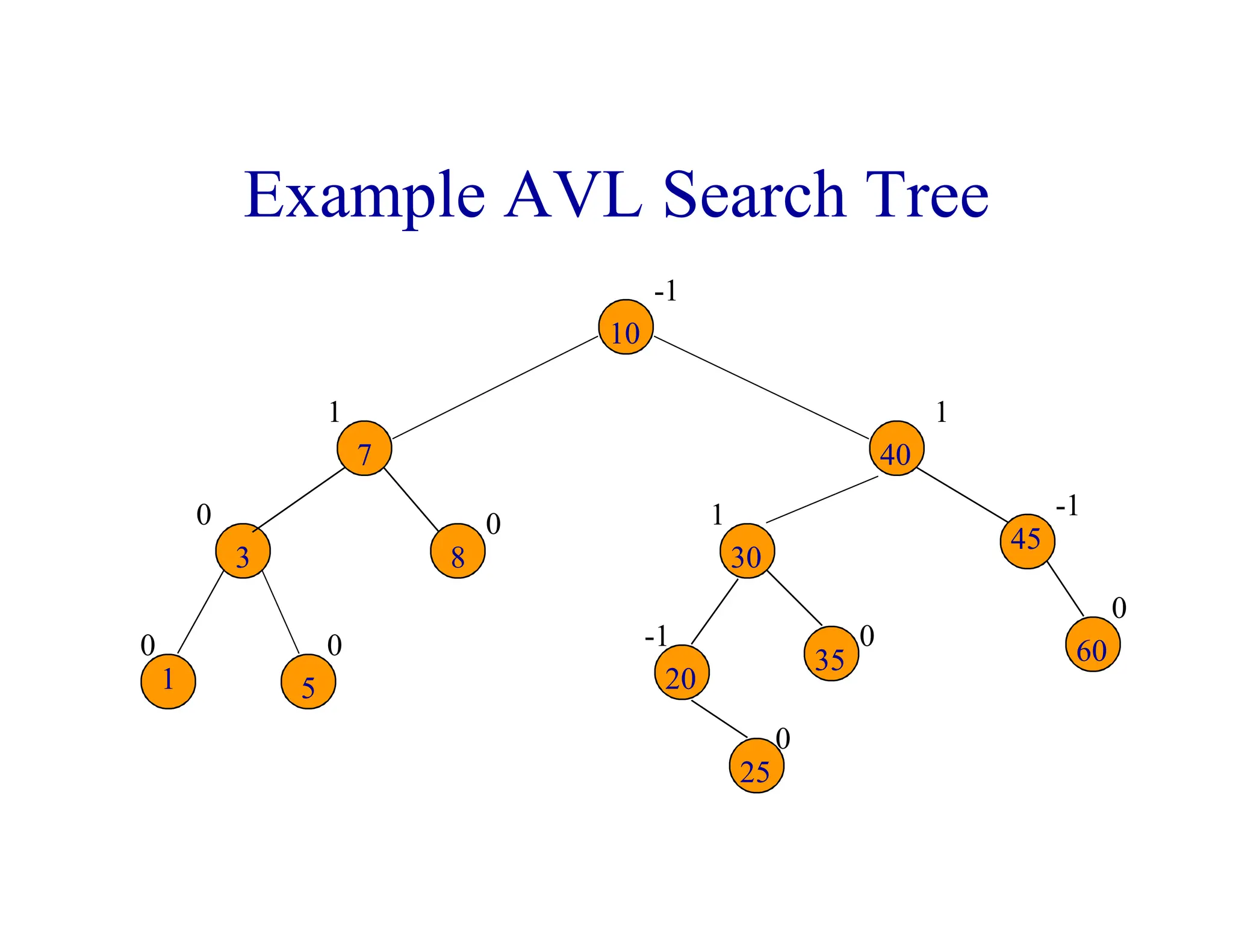
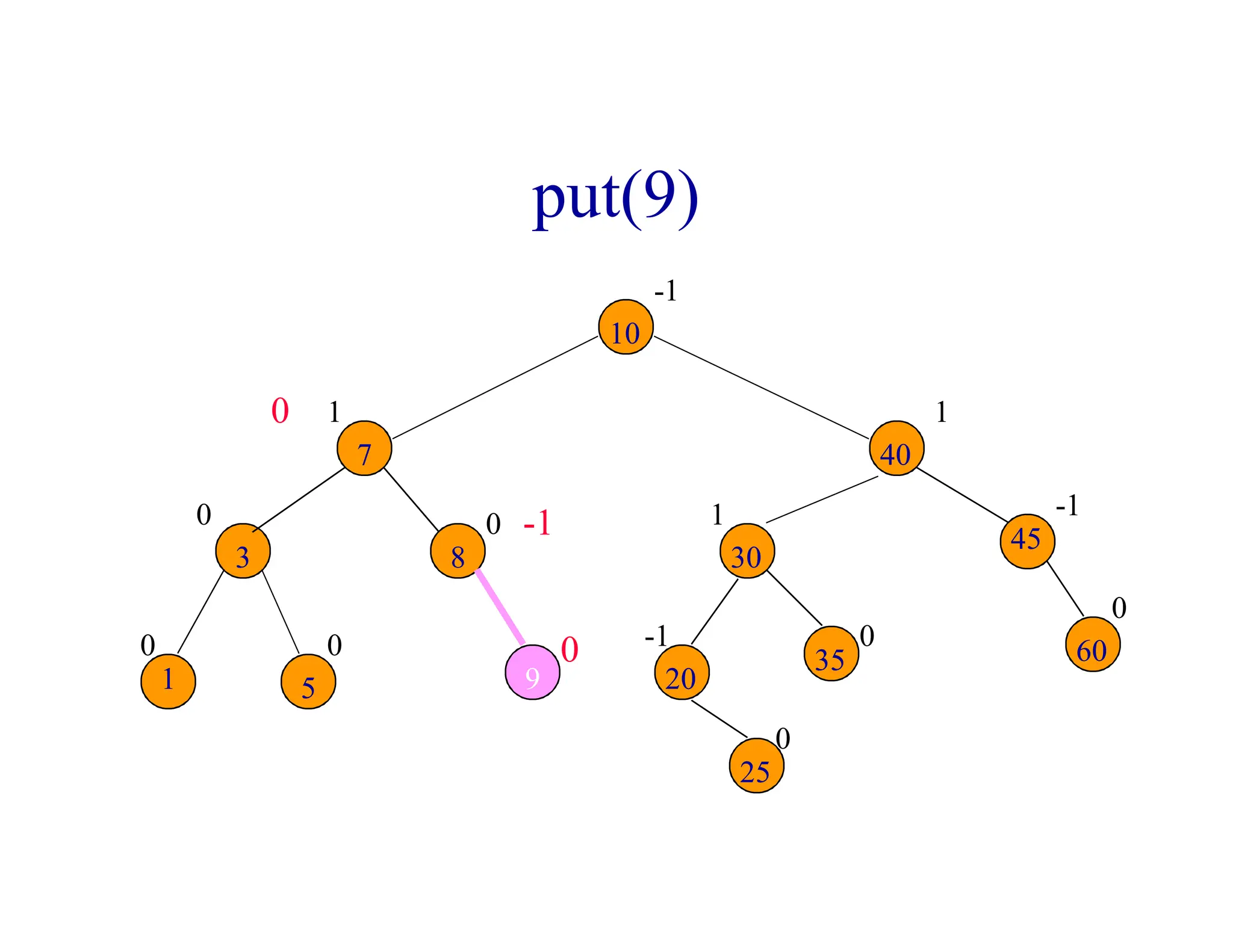
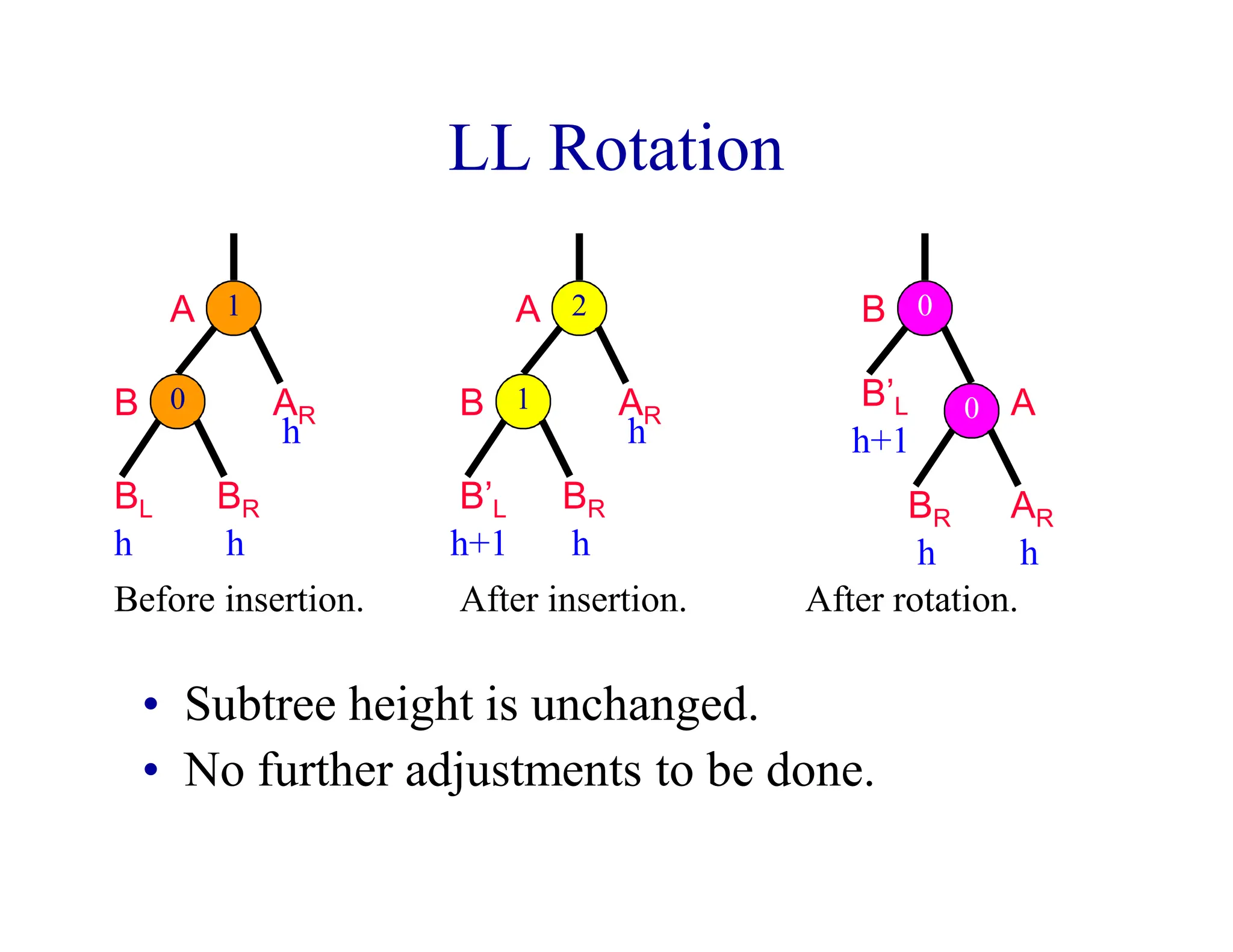
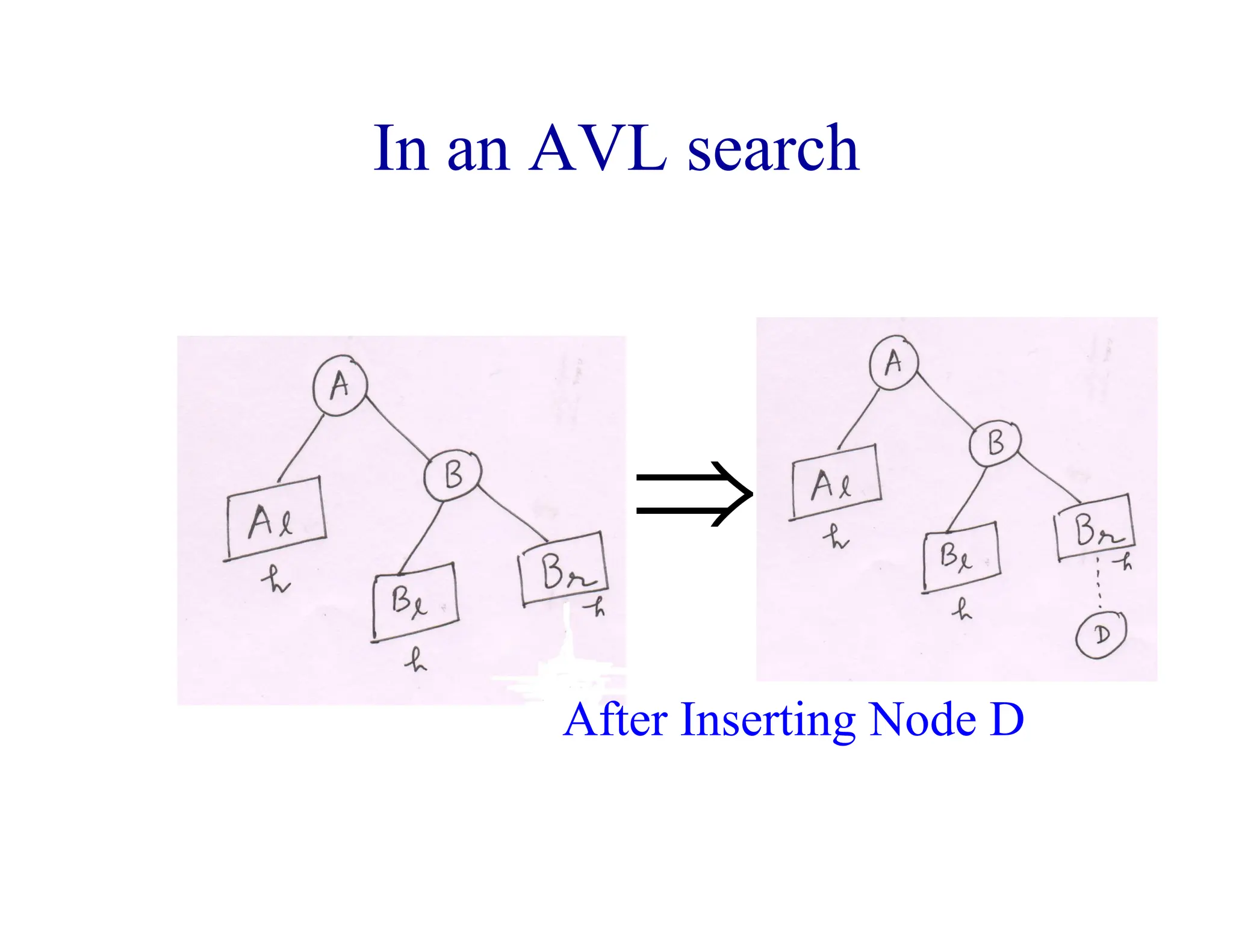
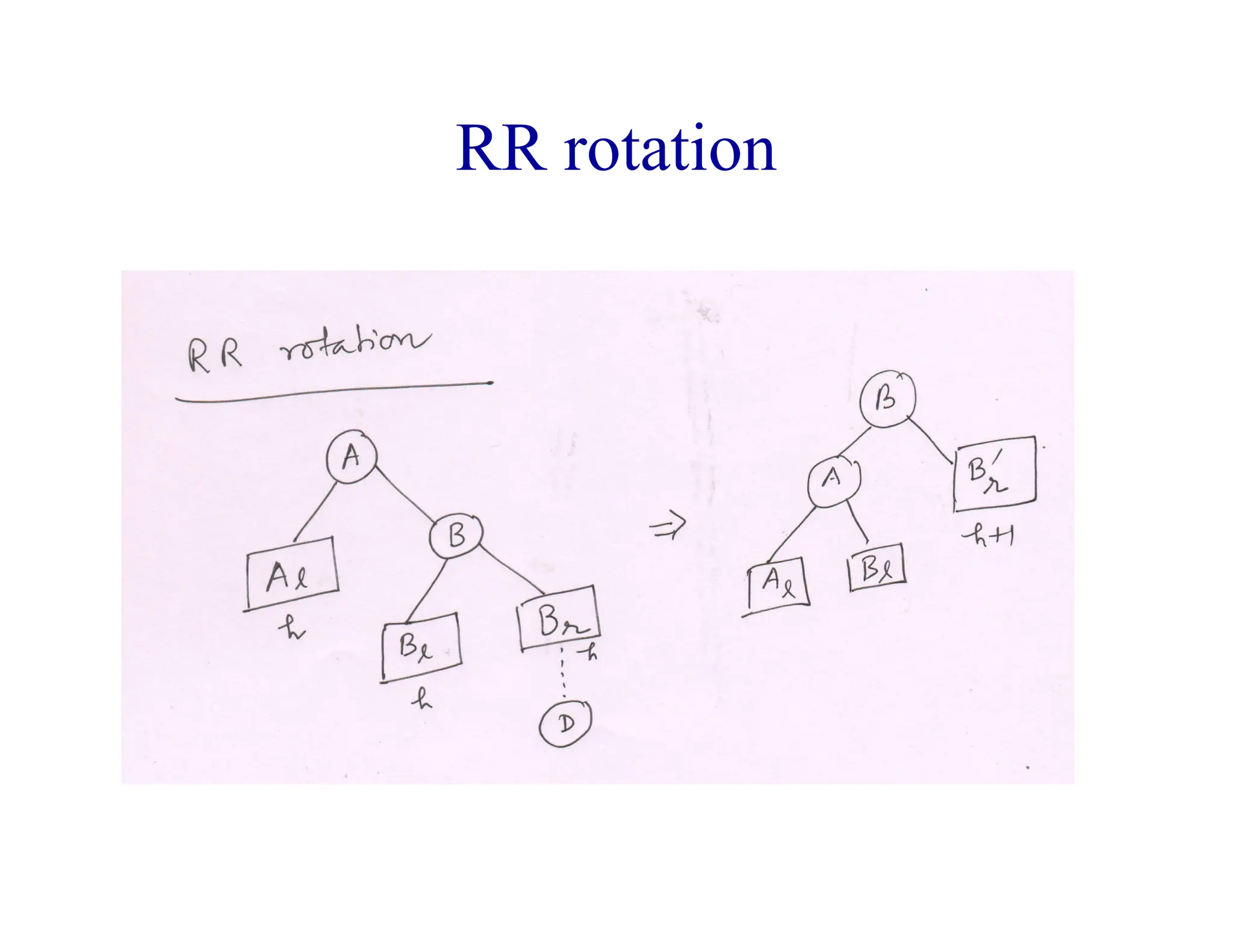
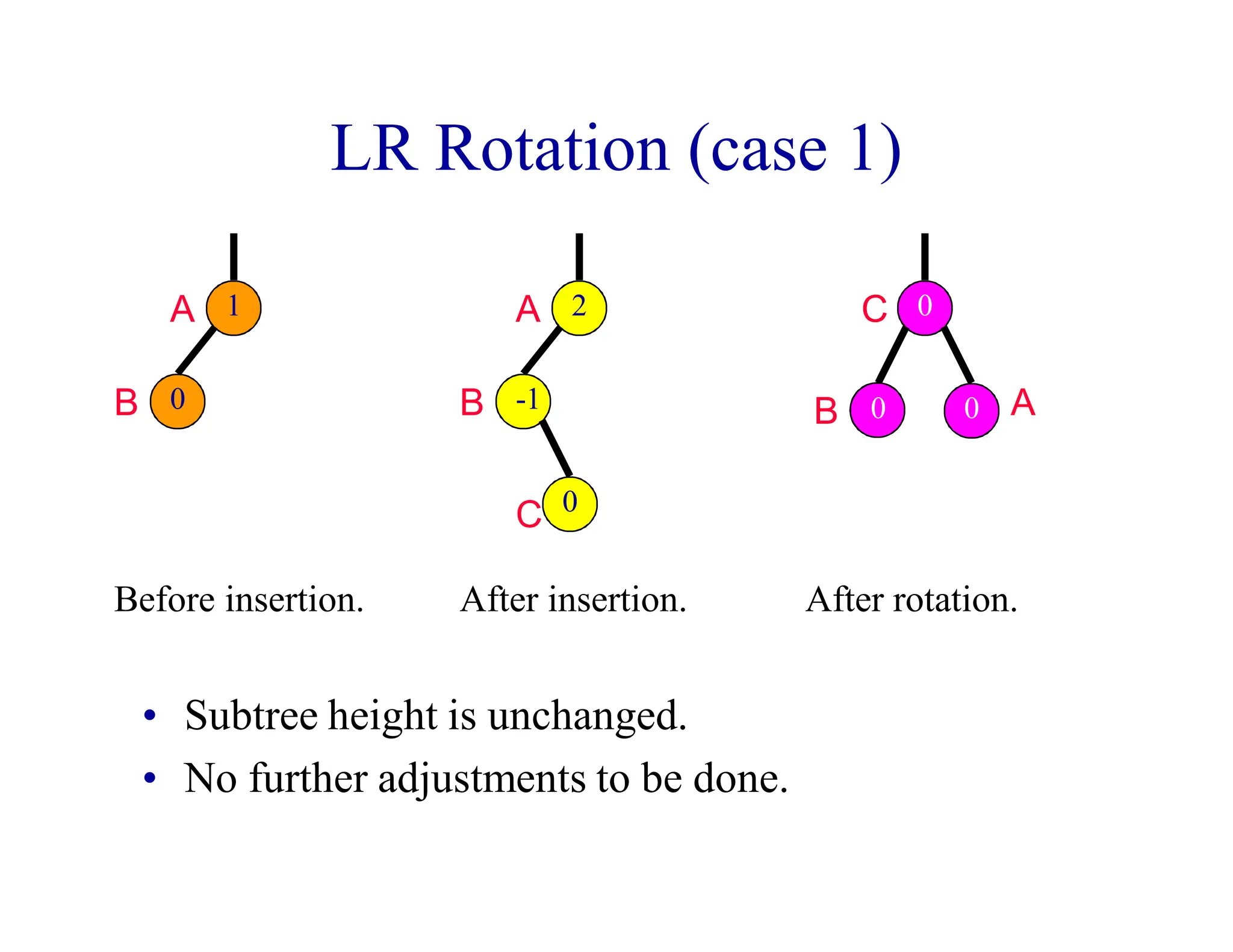
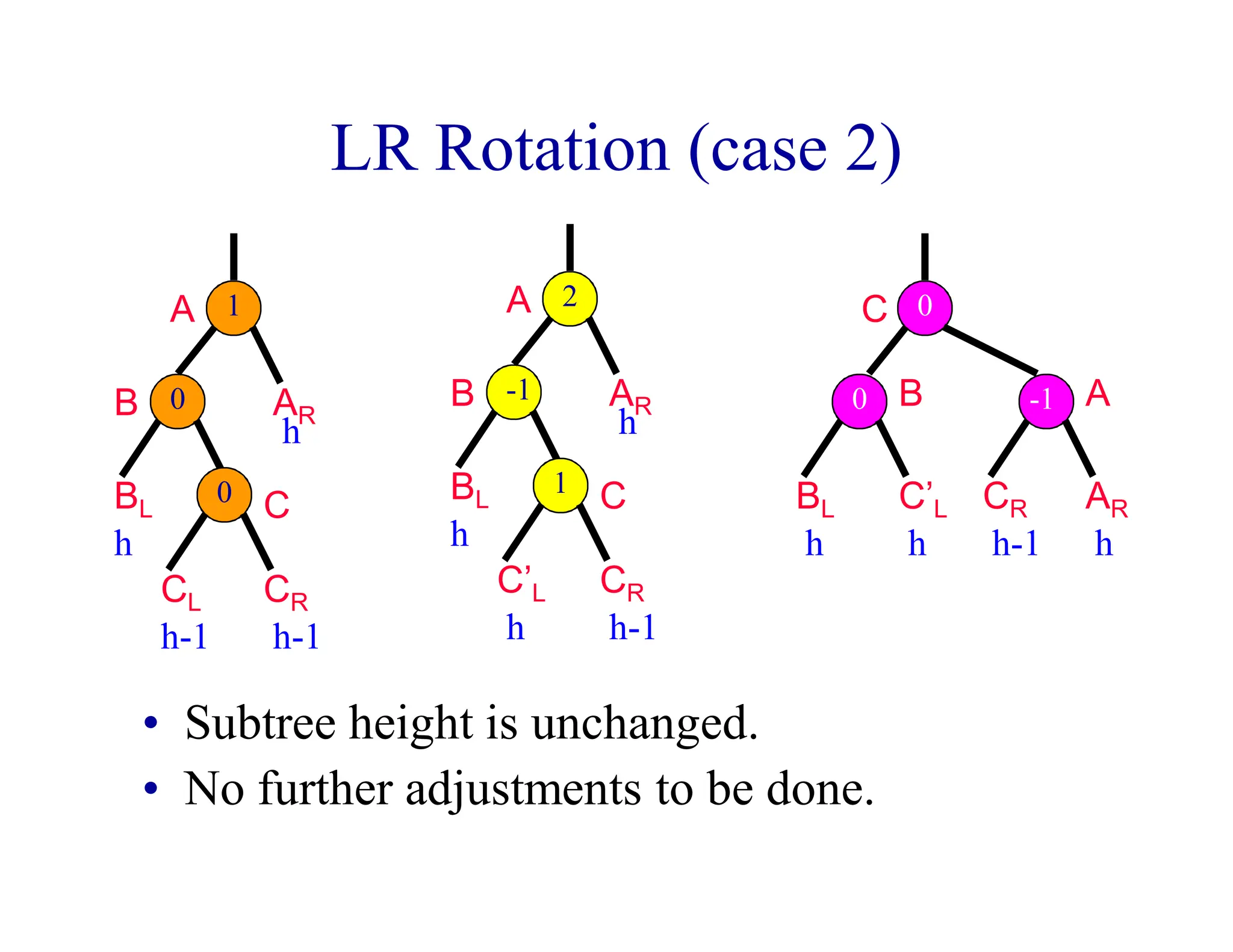
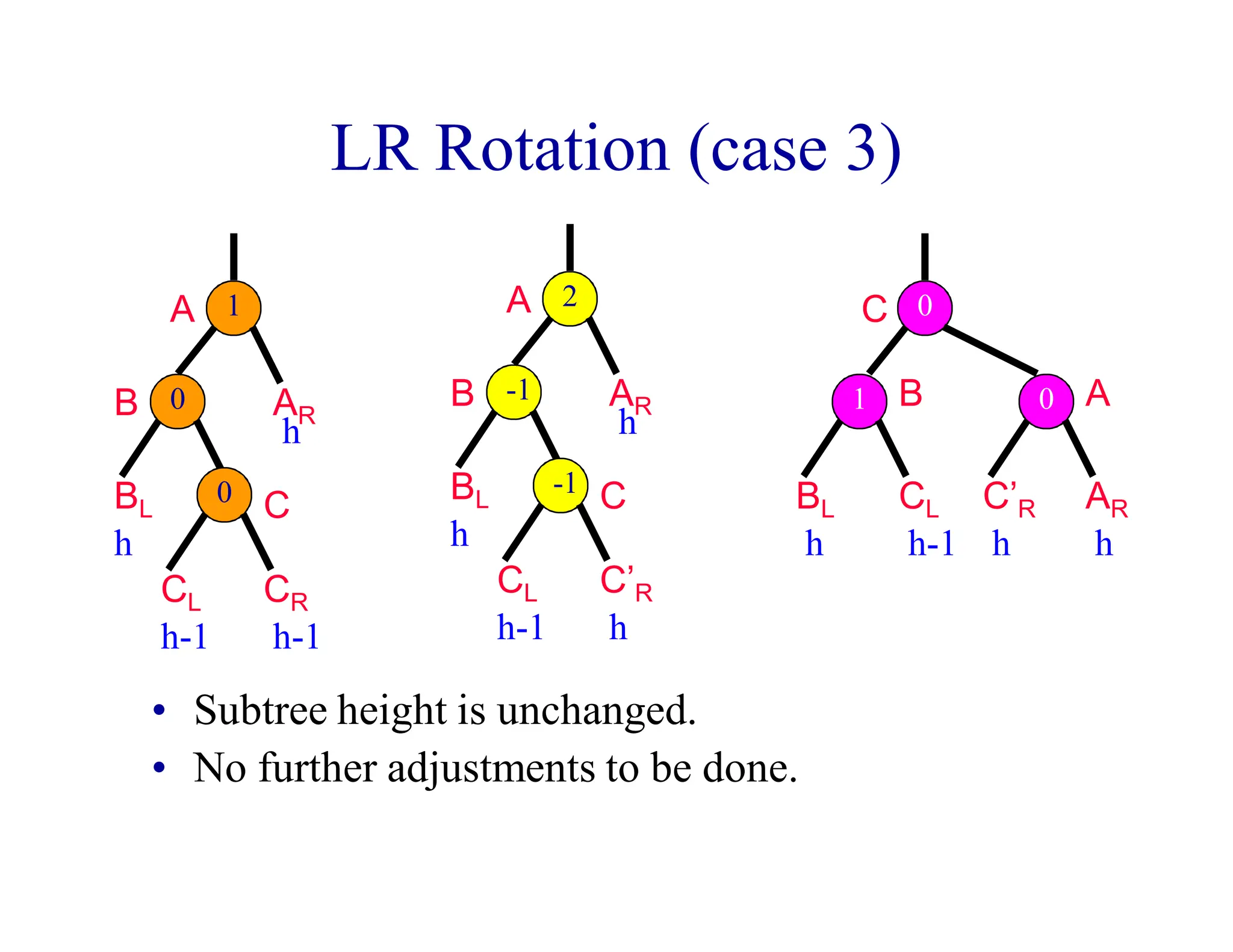
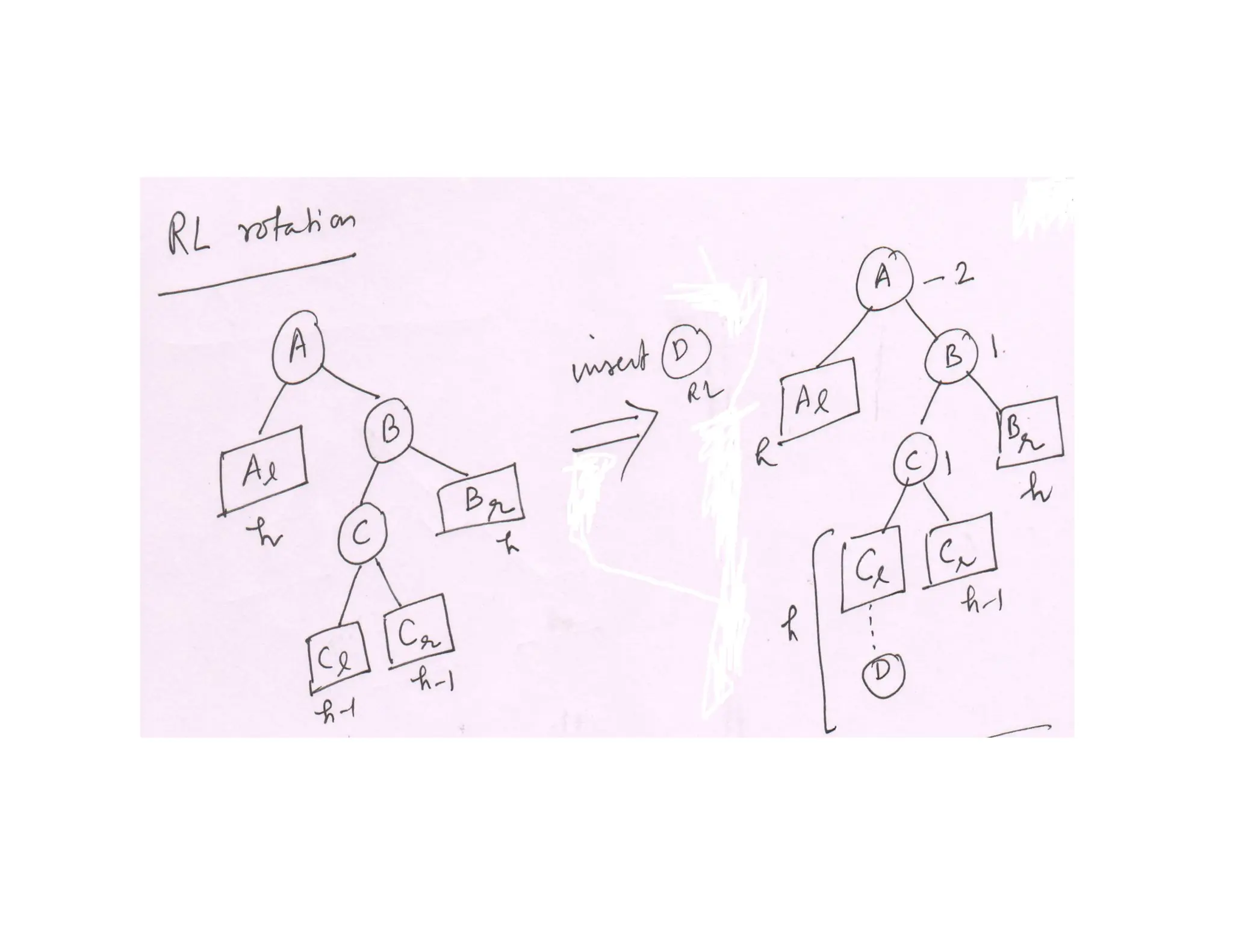
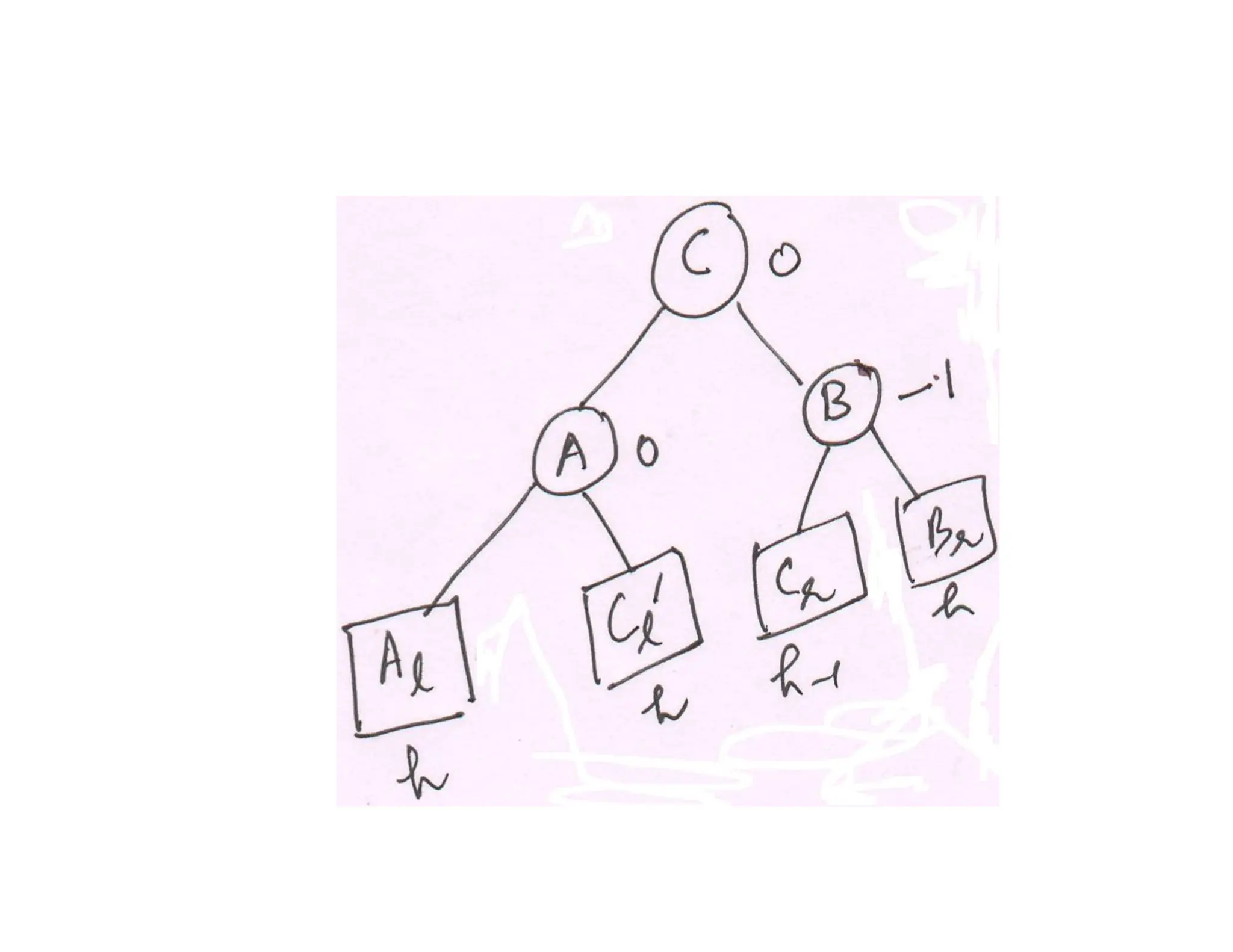
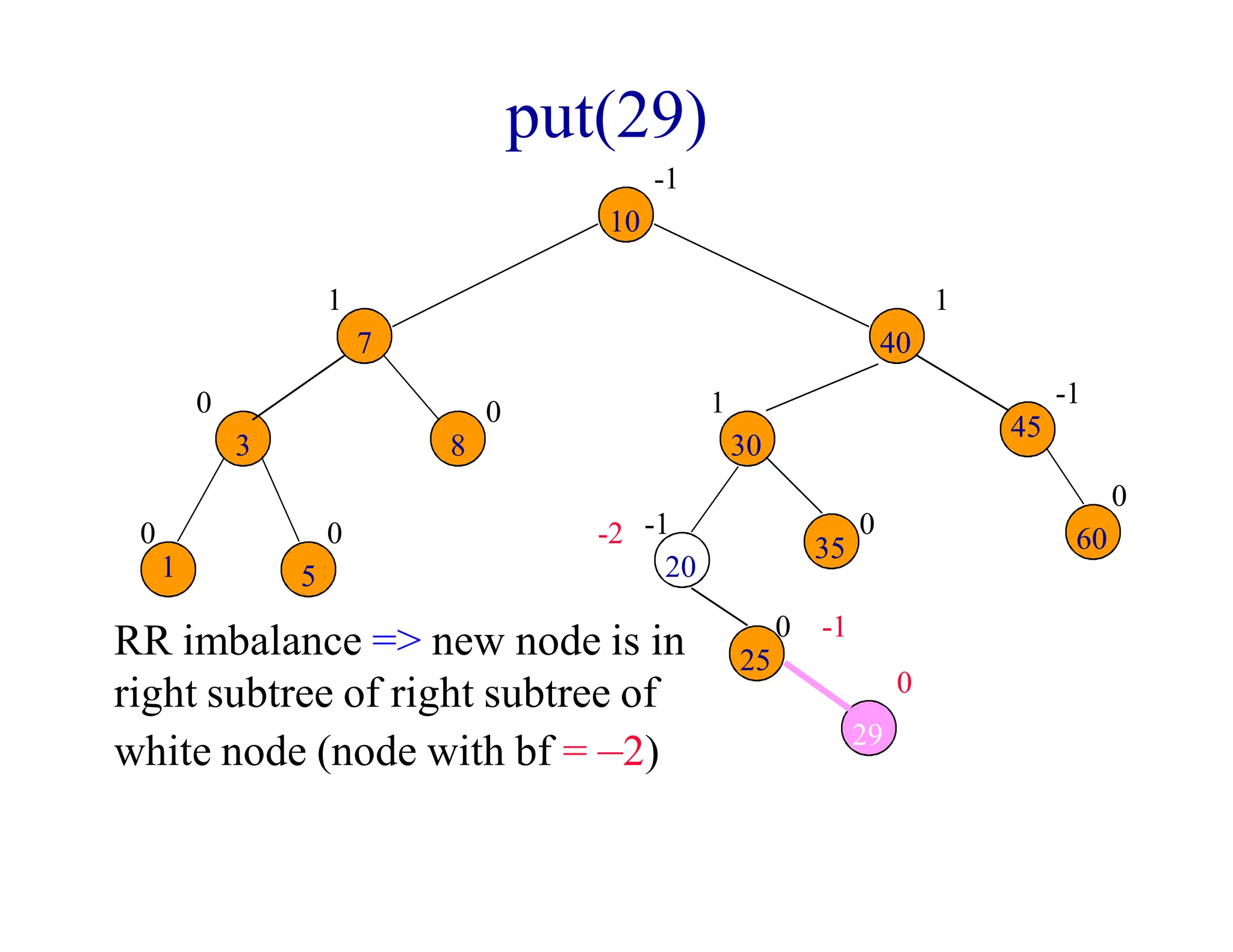
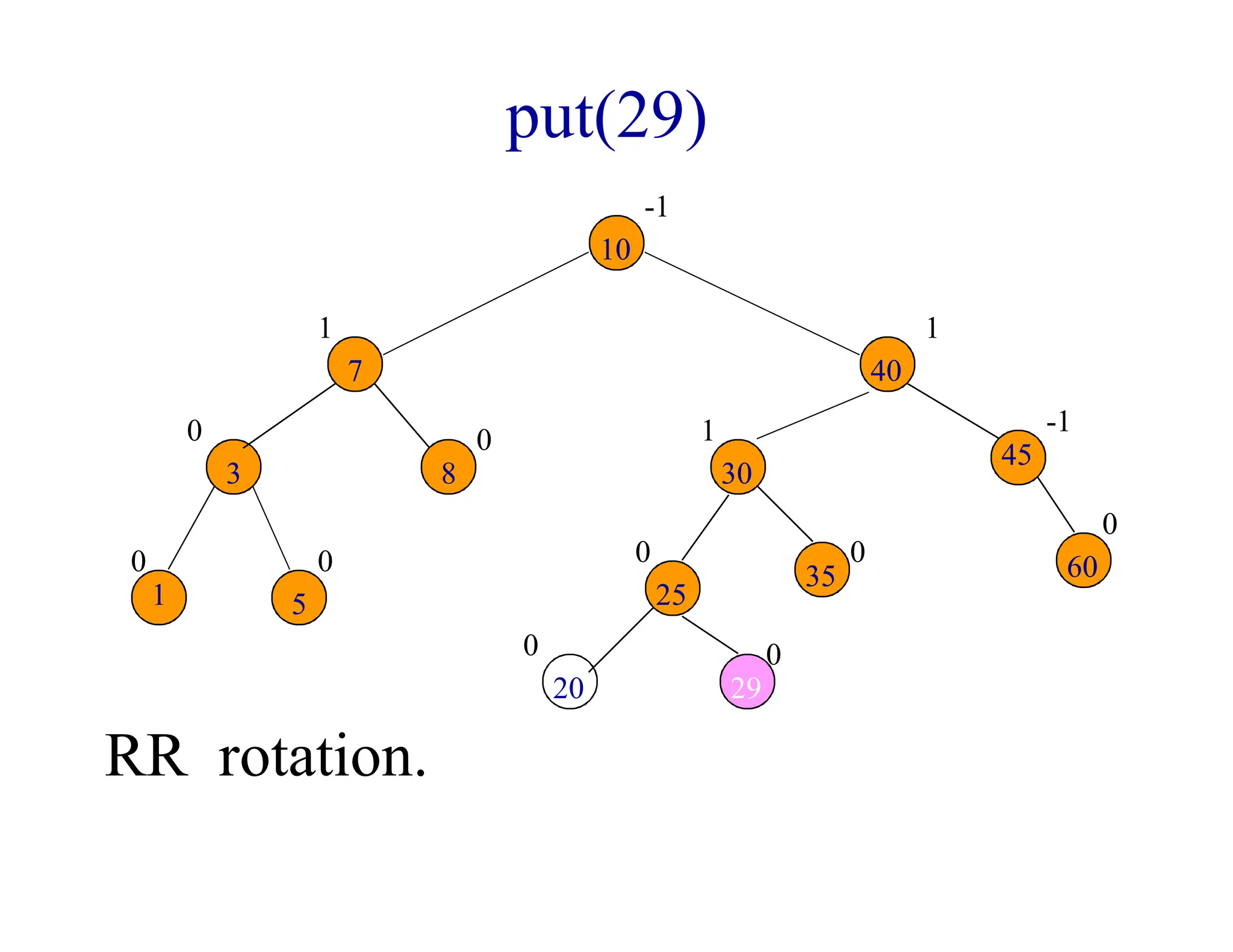
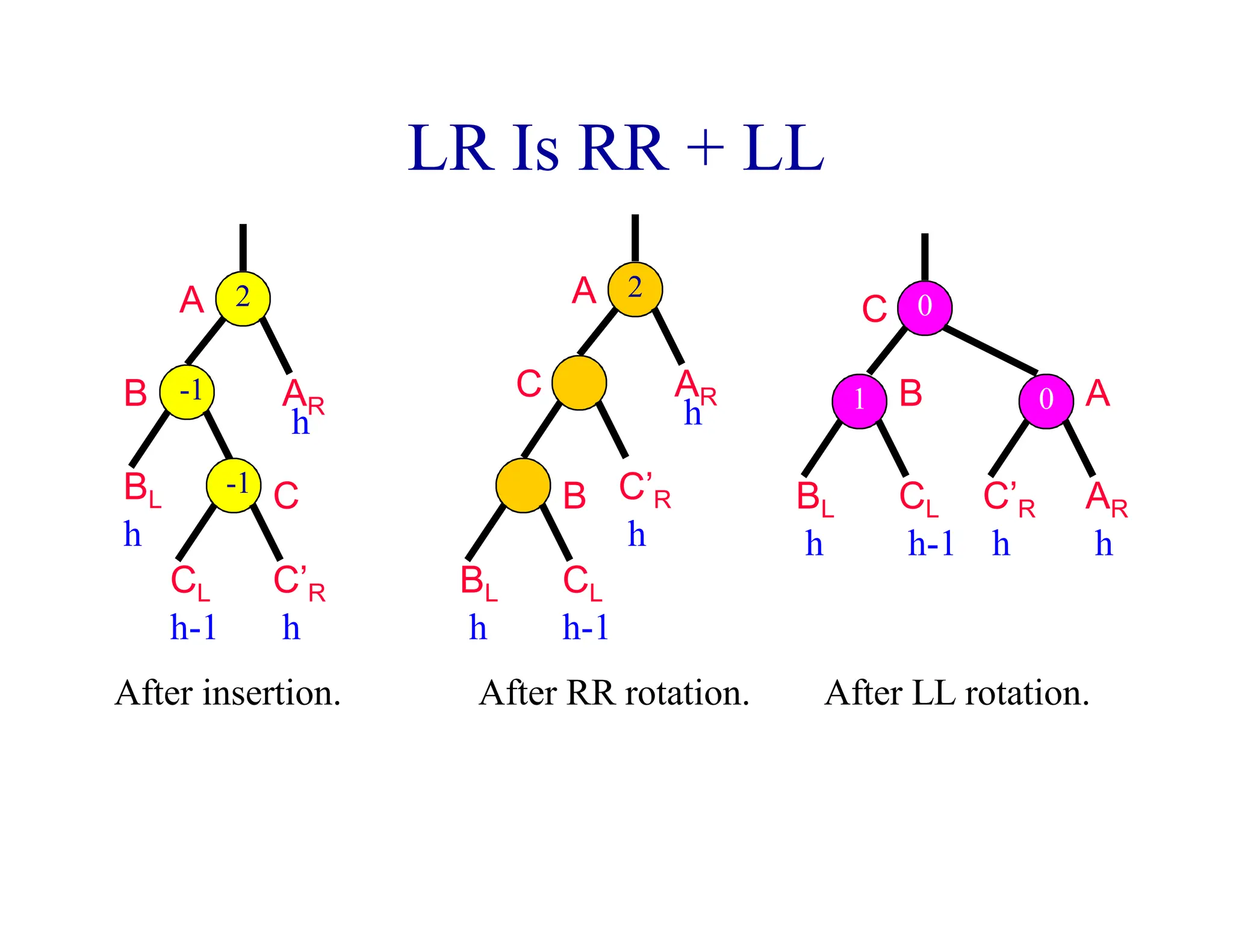
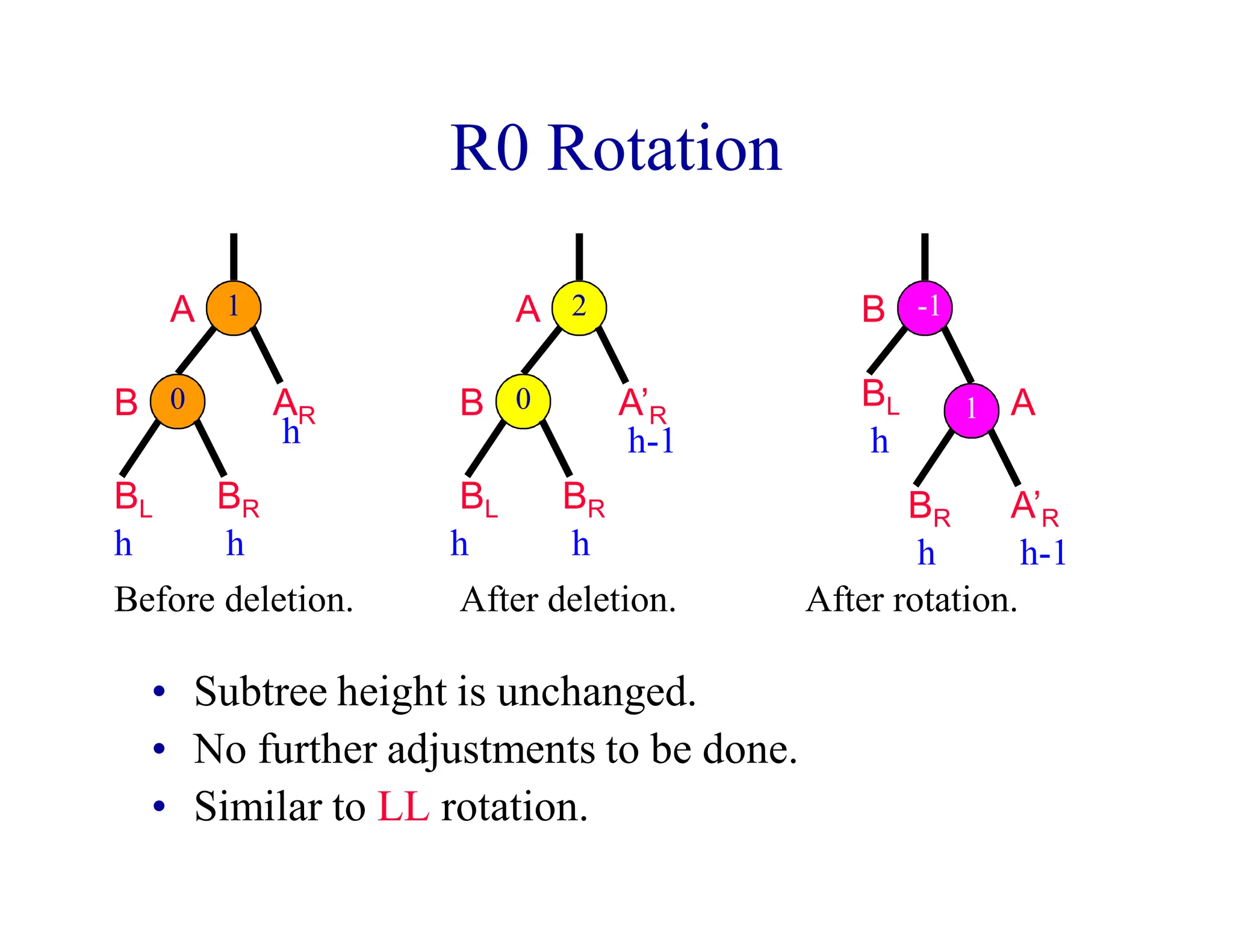
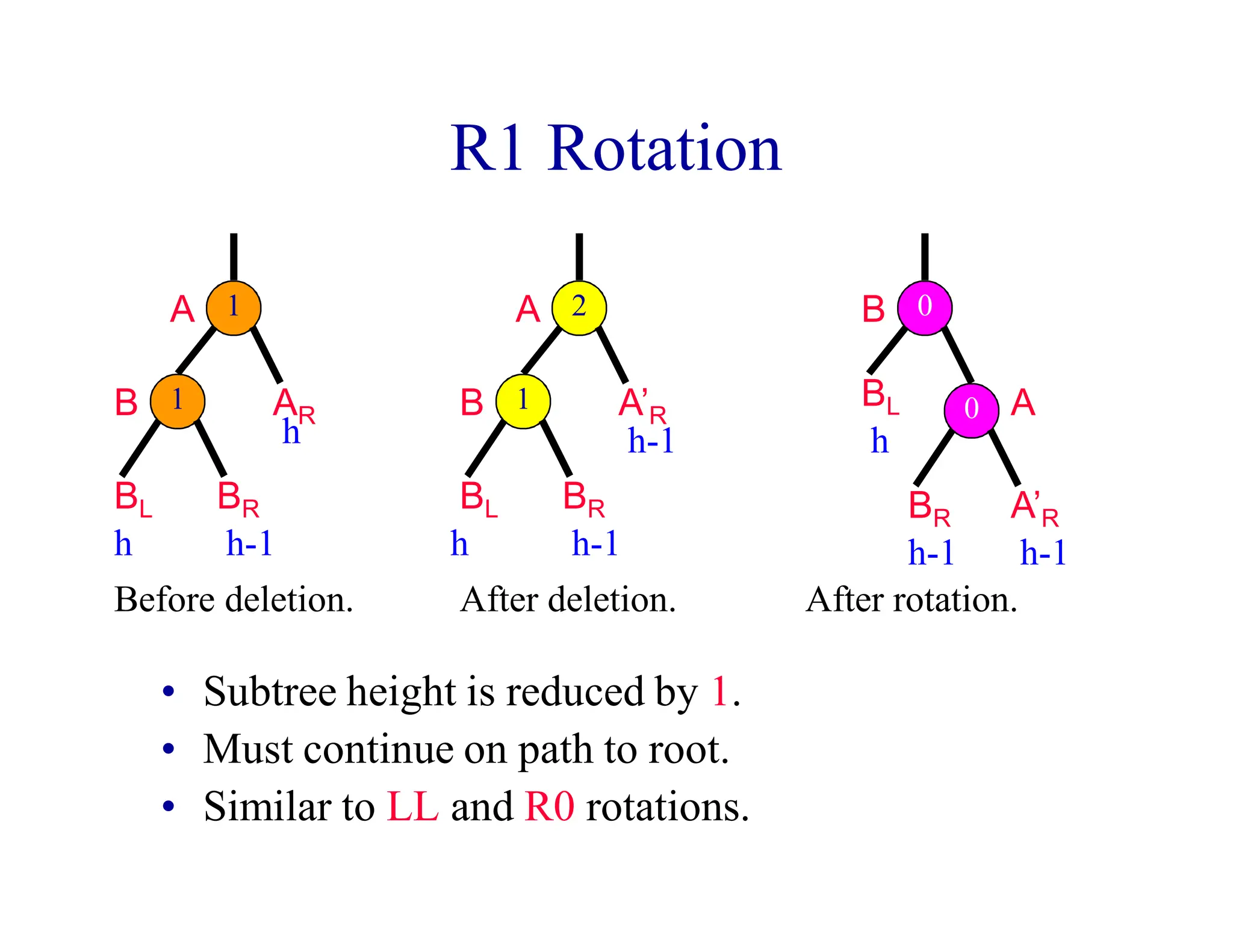
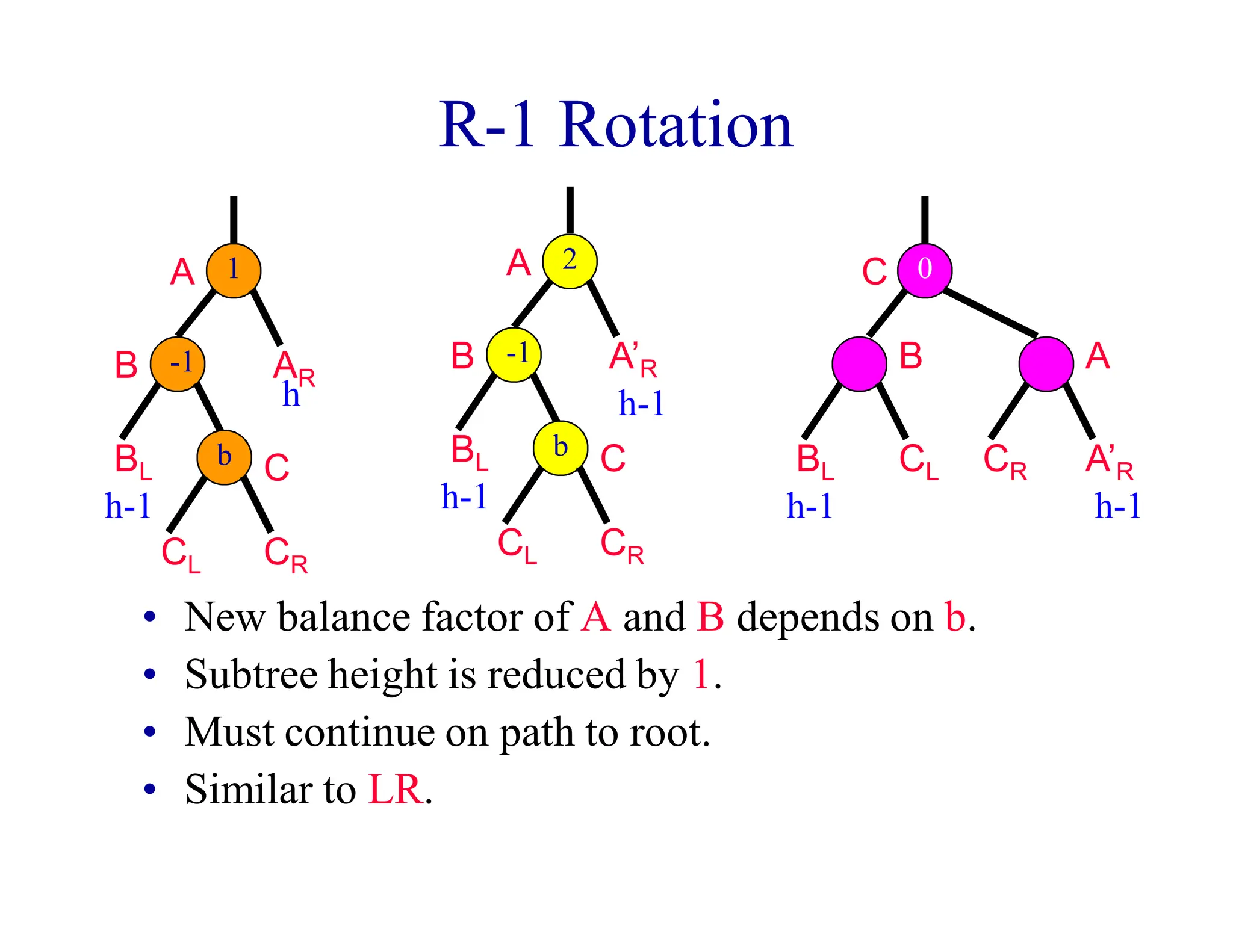
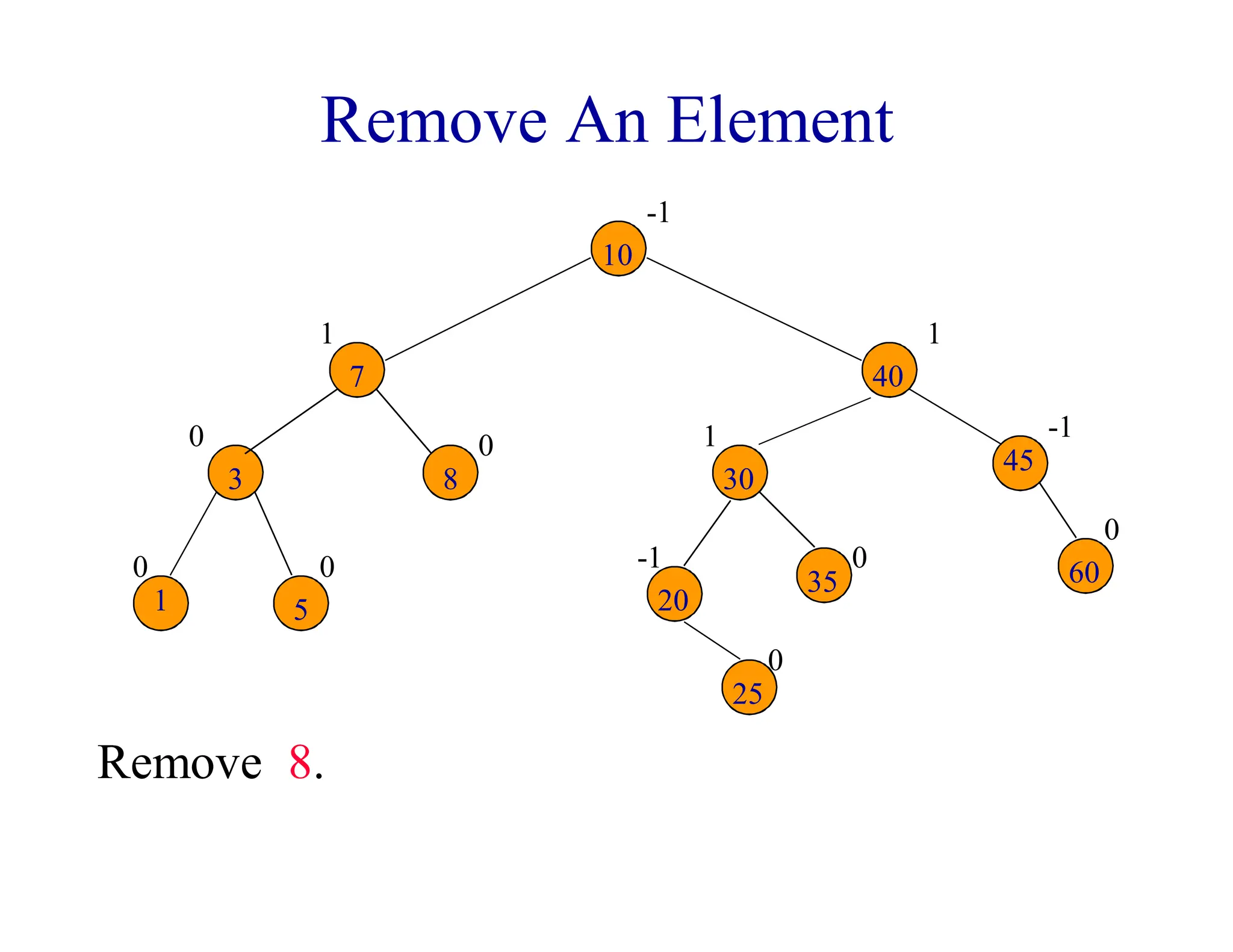
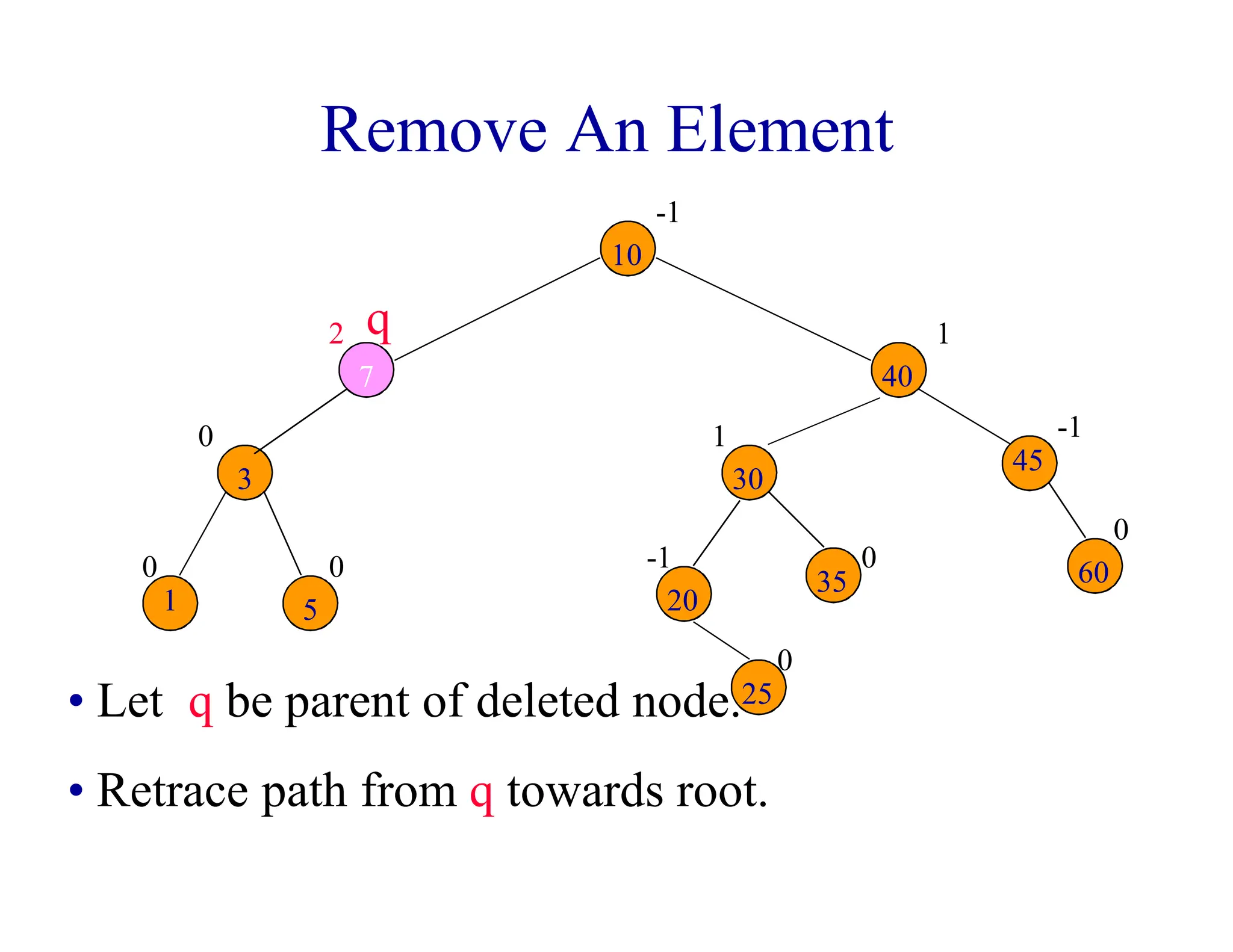
- AVL trees are binary search trees where the balance factor of every node is between -1 and 1, ensuring the tree remains balanced during insertions and deletions. - When a node's balance factor becomes 2 or -1 after an insertion or deletion, rotations are performed to balance the tree. Single rotations are LL or RR, double rotations are LR or RL. - Rotations may be needed during insertion to balance the tree. Deletions may require rebalancing along the path from the deleted node to the root. At most one rotation is required per insertion, but deletions could require O(log n) rotations.

1. AVL Trees
• binary tree
• for every node x, define its balance factor
balance factor of x = height of left subtree of x
– height of right subtree of x
• balance factor of every node x is – 1, 0, or 1
• log2 (n+1) <= height <= 1.44 log2 (n+2)

2. Example AVL Search Tree
0 0
0 0
1
0
-1 0
1
0
-1
1
-1
10
7
8
3
1 5
30
40
20
25
35
45
60

3. put(9)
0 0
0 0
1
0
-1 0
1
0
-1
1
-1
9
0
-1
0
10
7
8
3
1 5
30
40
20
25
35
45
60

4. put(29)
0 0
0 0
1
0
0
1
0
-1
1
-1
10
7
8
3
1 5
30
40
20
25
35
45
60
29
0
-1
-1
-2
RR imbalance => new node is in
right subtree of right subtree of
white node (node with bf = –2)

5. 0 0
0 0
1
0
0
1
0
-1
1
-1
10
7
8
3
1 5
30
40
25
35
45
60
0
RR rotation.
20
0
29
put(29)

6. Insert/Put
• Following insert/put, retrace path towards root
and adjust balance factors as needed.
• Stop when you reach a node whose balance
factor becomes 0, 2, or –2, or when you reach
the root.
• The new tree is not an AVL tree only if you
reach a node whose balance factor is either 2 or
–2.
• In this case, we say the tree has become
unbalanced.

7. A-Node
• Let A be the nearest ancestor of the newly
inserted node whose balance factor becomes
+2 or –2 following the insert.
• Balance factor of nodes between new node
and A is 0 before insertion.

8. Imbalance Types
• RR … newly inserted node is in the right
subtree of the right subtree of A.
• LL … left subtree of left subtree of A.
• RL… left subtree of right subtree of A.
• LR… right subtree of left subtree of A.

9. LL rotation

10. LL Rotation
• Subtree height is unchanged.
• No further adjustments to be done.
Before insertion.
1
0
A
B
BL BR
AR
h h
h
A
B
B’L BR
AR
After insertion.
h+1 h
h
B
A
After rotation.
BR
h
AR
h
B’L
h+1
0
0
1
2

11. Example

12. RR rotation

13. In an AVL search
After Inserting Node D


14. RR rotation

15. Example

16. LR Rotation (case 1)
• Subtree height is unchanged.
• No further adjustments to be done.
Before insertion.
1
0
A
B
A
B
After insertion.
C
C
A
After rotation.
B
0
-1
2
0 0
0

17. LR Rotation (case 2)
• Subtree height is unchanged.
• No further adjustments to be done.
C
A
CR
h-1
AR
h
1
0
A
B
BL
CR
AR
h
h-1
h
0
CL
h-1
C
A
B
BL
CR
AR
h
h-1
h
C’L
h
C
B
BL
h
C’L
h
1
-1
2
0 -1
0

18. LR Rotation (case 3)
• Subtree height is unchanged.
• No further adjustments to be done.
1
0
A
B
BL
CR
AR
h
h-1
h
0
CL
h-1
C
A
B
BL
C’R
AR
h
h
h
CL
h-1
C
-1
-1
2
C
A
C’R
h
AR
h
B
BL
h
CL
h-1
1 0
0

19. Example

20. RL Rotation

23. Single & Double Rotations
• Single
 LL and RR
• Double
 LR and RL
 LR is RR followed by LL
 RL is LL followed by RR

24. LR Is RR + LL
A
B
BL
C’R
AR
h
h
h
CL
h-1
C
-1
-1
2
After insertion.
A
C
CL
C’R
AR
h
h
BL
h
B
2
After RR rotation.
h-1
C
A
C’R
h
AR
h
B
BL
h
CL
h-1
1 0
0
After LL rotation.

25. Remove An Element
0 0
0 0
1
0
-1 0
1
0
-1
1
-1
10
7
8
3
1 5
30
40
20
25
35
45
60
Remove 8.

26. Remove An Element
0 0
0
2
0
-1 0
1
0
-1
1
-1
10
7
3
1 5
30
40
20
25
35
45
60
• Let q be parent of deleted node.
• Retrace path from q towards root.
q

27. New Balance Factor Of q
• Deletion from left subtree of q => bf--.
• Deletion from right subtree of q => bf++.
• New balance factor = 1 or –1 => no change in height of
subtree rooted at q.
• New balance factor = 0 => height of subtree rooted at q
has decreased by 1.
• New balance factor = 2 or –2 => tree is unbalanced at q.
q

28. Imbalance Classification
• Let A be the nearest ancestor of the deleted
node whose balance factor has become 2 or –2
following a deletion.
• Deletion from left subtree of A => type L.
• Deletion from right subtree of A => type R.
• Type R => new bf(A) = 2.
• So, old bf(A) = 1.
• So, A has a left child B.
 bf(B) = 0 => R0.
 bf(B) = 1 => R1.
 bf(B) = –1 => R-1.

29. R0 Rotation
• Subtree height is unchanged.
• No further adjustments to be done.
• Similar to LL rotation.
Before deletion.
1
0
A
B
BL BR
AR
h h
h
B
A
After rotation.
BR
h
A’R
h-1
BL
h
1
-1
A
B
BL BR
A’R
After deletion.
h h
h-1
0
2

31. R1 Rotation
• Subtree height is reduced by 1.
• Must continue on path to root.
• Similar to LL and R0 rotations.
Before deletion.
1
1
A
B
BL BR
AR
h h-1
h
B
A
After rotation.
BR
h-1
A’R
h-1
BL
h
0
0
A
B
BL BR
A’R
After deletion.
h h-1
h-1
1
2

33. R-1 Rotation
• New balance factor of A and B depends on b.
• Subtree height is reduced by 1.
• Must continue on path to root.
• Similar to LR.
1
-1
A
B
BL
CR
AR
h-1
h
b
CL
C
A
B
BL
CR
A’R
h-1
h-1
CL
C
b
-1
2
C
A
CR A’R
h-1
B
BL
h-1
CL
0

35. Number of Rebalancing Rotations
• At most 1 for an insert.
• O(log n) for a delete.

36. Rotation Frequency
• Insert random numbers.
 No rotation … 53.4% (approx).
 LL/RR … 23.3% (approx).
 LR/RL … 23.2% (approx).