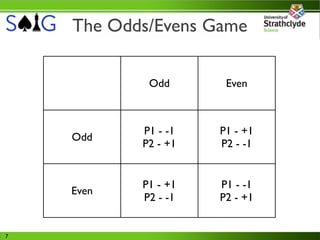
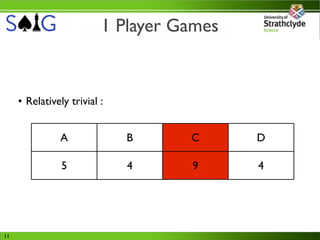
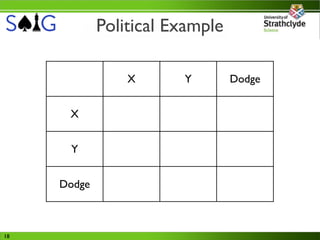
This document outlines the content of the first lecture in an eight-part series on game theory within a fourth-year AI course, targeting students with prior AI knowledge. Key topics include the prisoner's dilemma, game types (zero-sum vs. non-zero-sum), equilibrium strategies, and the role of utility in decision-making. The lecture emphasizes the importance of understanding strategic interactions and potential irrational behaviors in competitive scenarios.

1. 52.426 - 4th Year AI
Game AI
Luke Dicken
Strathclyde AI and Games Group

2. Background
• This is the 1st lecture in an 8 lecture series that
constitutes the 2nd half of the course.
• Target audience is a 4th year class that has had
exposure to AI previously
‣ 3rd year - Agent-based systems
‣ 4th year (1st half) - Algorithms and Search, bin-packing
• Although it is a Game AI module, the course itself is
a general AI class, many non-games students.
2

3. The Prisoner's Dilemma
• Imagine you and another person are arrested
• Keep silent? Or betray the other person?
• They have the same choice...
3

4. Prisoners Dilemma
Confess Silent
P1 - 5yrs P1 - Free
Confess
P2 - 5yrs P2 - 20yrs
P1 - 20yrs P1 - 1yr
Silent
P2 - Free P2 - 1yr
4

5. Questions
• Does it help to know the other person?
• Is it better to be ignorant of your opponent than incorrectly
predict their actions?
• Do you want to minimise total time in jail, or your time in
jail?
5

6. The Odds/Evens Game
• Player 1 picks up some number of marbles.
• Player 2 guesses if amount is odd or even.
6

7. The Odds/Evens Game
Odd Even
P1 - -1 P1 - +1
Odd
P2 - +1 P2 - -1
P1 - +1 P1 - -1
Even
P2 - -1 P2 - +1
7

8. Questions
• Player 1 played odd last time, what should Player 2 guess this
time?
• Can Player 1 vary their strategy such that Player 2 can never
guess it?
8

9. Intro to Game Theory

10. Game Theory 101
• What we've just seen are examples "games"
• Anytime we are talking about competing with other people
for a reward, we can call it a "game"
• Game Theory is a branch of mathematics that formally
defines how best to play these games.
10

11. 1 Player Games
• Relatively trivial :
A B C D
5 4 9 4
11

12. 2 Player Games
• Things get more complicated when there’s a second player.
• How can you predict what that person will do?
• Can you ensure that you will do well regardless of the other
player?
• This is the essence of Game Theory.
12

13. A Game's "Sum"
• Games can be "zero-sum" or "non-zero sum"
• If a game is zero-sum then the two players are directly
competing - for one to win X, the other must lose X
• Contrast this a game where the two players are not
completely opposed.
‣ E.g. Prisoner's Dilemma
• Zero-sum games allow us to make assumptions about how
players will act but they are not the general case.
13

14. 2 Player Zero-Sum Games
• Although it's a special case, this comes up very very often in
the real world.
‣ Elections, gambling, corporate competition
• Previously shown payoff for both players - in zero-sum this
isn’t necessary
‣ The more Player 1 wins, the more Player 2 loses
14

15. Equilibrium Points
• A property of some games is that there is a single “solution”
• If Player 1 changes strategy from their Equilibrium Strategy,
they can only do worse (assuming Player 2 does not change)
• Likewise Player 2 cannot change their strategy unilaterally
and do any better either.
• For both players, this is the best they can hope to achieve
15

16. The “Value” of a Game
• The “Value” of a game is “the rationally expected outcome”
• For games that have equilibrium points, the Value is the
reward of the equilibrium strategies.
‣ Player 1 can’t do worse than this value.
‣ Player 2 can prevent Player 1 from doing better.
16

17. Political Example
• Two candidates are deciding what position to take
on an issue.
• There are three options open to each of them
‣ Support X
‣ Support Y
‣ Duck the issue
17

18. Political Example
X Y Dodge
X
Y
Dodge
18

19. Political Example
X Y Dodge
X 45% 50% 40%
Y 60% 55% 50%
Dodge 45% 55% 40%
Payoff Matrix wrt Player 1’s vote share
19

20. Political Example
• Whatever Player 1 does, Player 2 does best if they
dodge the issue.
• Whatever Player 2 does, Player 1 does best if they
support Y.
20

21. Dominant Strategies
• Sometimes, a potential strategy choice is just bad.
• Recall the 1-player game - one strategy was ALWAYS better.
• This can happen in 2-player games too.
• More formally, Strategy A dominates Strategy B iff for every
move the opponent might choose, A always gives a better
result.
• Dominated strategies can safely be ignored then.
‣ A rational opponent would never play them, so you
needn’t consider situations where they would.
21

22. Domination
i ii iii
A 19 0 1
B 11 9 3
C 23 7 -3
22

23. Domination
x ii iii
A x 0 1
B x 9 3
C x 7 -3
iii dominates i
(remember: from Player 2’s perspective, lower = better)
23

24. Domination
x ii iii
x x x x
B x 9 3
x x x x
Now, B dominates both A and C
Player 1 should choose B.
24

25. Domination
x x iii
x x x x
B x x 3
x x x x
As Player 1 will choose B, Player 2 should choose iii
Note that this is an equilibrium point
25

26. Non-Zero Sum Games
• Recall the Prisoner’s Dilemma problem.
• In this game, the two players were not completely
opposed
‣ Cooperation as well as competition
• This means that a lot of the assumptions that we’ve
made about what the players want to achieve don’t
hold
26

27. Prisoners Dilemma
Confess Silent
P1 - 5yrs P1 - Free
Confess
P2 - 5yrs P2 - 20yrs
P1 - 20yrs P1 - 1yr
Silent
P2 - Free P2 - 1yr
27

28. Some More Examples
• Which would you prefer, a guaranteed £1 or an even chance
at £3?
28

29. Some More Examples
• Suppose you lose concert tickets that cost you £40 to buy.
Would you replace them for another £40 or do something
else that night?
29

30. Some More Examples
• If 1% of people your age and health die in a given year, would
you be prepared to pay £1,000 for £100,000 of life
insurance?
30

31. Some More Examples
• You go to the store to buy a new video game costing £40.
You find you've lost some money, also totalling £40, but you
still have enough left to buy the game - do you?
31

32. Some More Examples
• Which would you prefer, a guaranteed £1,000,000 or an even
chance at £3,000,000?
32

33. Some More Examples
• If 0.1% of people your age and health die in a given year,
would you be prepared to pay £10 for £10,000 of life
insurance?
33

34. Something else is
happening...

35. Utility Theory
• "Utility" is an evaluation of how much use a particular result
is.
• It allows us to compare things "through the eyes of the
player" rather than just mathematically.
‣ £1 and £3 are relatively interchangeable, and £1 is not significant.
‣ £1,000,000 is significant, and £3,000,000 is not three times as
significant.
35

36. Prisoners Dilemma
Do we want an optimal solution for one player?
Or for both?
Confess Silent
P1 - 5yrs P1 - Free
Confess
P2 - 5yrs P2 - 20yrs
P1 - 20yrs P1 - 1yr
Silent
P2 - Free P2 - 1yr
36

37. Irrational Actions
• Utility functions for humans is beyond the scope of
this session.
• Behavioural Economics
‣ “Predictably Irrational” Dan Ariely
• Be aware that players may not be rational.
‣ And we can exploit this to beat them even more :D
37

38. Summary
• Fundamentals of Game Theory
• Rational play for 2 Player Zero Sum games
• Difference of a Non-Zero Sum game
• Introduction to irrational play
38

39. Next Lecture
• Fun With Probability!
• How Spam Filters Work (Sort of)
• Mixed Strategies in Games
• ...And More
39