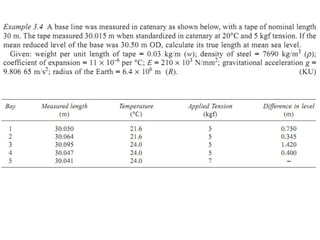
The document discusses various corrections that must be applied to distance measurements taken with tapes. It describes 6 types of corrections: 1. Temperature corrections account for tape expansion or contraction due to temperatures different from the standard 20°C measurement condition. 2. Tension corrections account for differences between the applied tension and standard tension used during tape calibration. 3. Sag corrections account for the catenary shape of a tape suspended between two points and ensure the measured distance matches the horizontal distance. 4. Slope corrections convert measured sloped distances to equivalent horizontal distances. 5. Standardization corrections account for tape length changes due to use over time. 6. Altitude corrections reduce measured distances to a standard

1. Distance Corrections

2. Distance Corrections
(measured with Tapes)

3. Distance Corrections
 Tapes come in a variety of lengths and materials. For
engineering work the lengths are generally10m, 30m, 50m
and 100m.
 Various materials of tapes includes linen, steel, invar (35%
Nickel and 65% Steel).
 Standard Conditions for distance measurement with tape:
 Temperature = 20 o
C
 Tension = 50 to 80 N

4. Equipments Required:
1. Ranging rods, made of wood or steel, 2 m long and 25 mm
in diameter, painted alternately red and white, with a pointed
metal shoe to allow it to be thrust into the ground. They are
generally used to align a straight line between two points.
2. Chaining arrows to mark the tape lengths when measured
distance is greater than the tape length.
3. Spring balances generally
used with roller-grips or
tape clamps to firmly grip
the tape when the standard
tension is applied.

5. Equipments Required
4. Field thermometers are also necessary to record the
tape temperature at the time of measurement.
5. Hand levels may be used to establish the tape
horizontal.
6. Plumb-bobs may be necessary if stepped taping is
used.
7. Measuring plates are necessary in rough ground, to
afford a mark against which the tape may be read.

6. Procedure:
1. Lining in – shortest distance between two points is a straight
line.
2. Applying tension – rear end of tape is held and another end is
stretched by applying required tension.
3. Plumbing – horizontal distance requires tape to be horizontal.
4. Marking tape lengths – each application of the tape requires
marking using chaining pins to obtain total length.
5. Reading the tape – the graduated tape must be read correctly.
6. Recording the distance – the total length must be reported and
recorded correctly.

7. Procedure
7. The mean result is then corrected for:
 Tape standardization.
 Slope.
 Temperature.
 Tension (if necessary).
7. The final total distance may then be reduced to its
equivalent MSL or mean site level.

8. Standardization:
 During a period of use, a tape will gradually alter in
length for a variety of reasons.
 A reference tape of known length under standard
condition must be used to check the measuring tape.
 The tape may then be specified as being 30.003 m at
20°C and 70 N tension or as 30 m exactly, at a
temperature other than standard.

9. Distance Adjustment:
 No measurements can be performed perfectly, so all
measurements contains some error, which needs to eliminated
by applying corrections.
 Various systematic errors include:
1. Temperature
2. Tension
3. Sag
4. Slope
5. Altitude

10. 1. Temperature Correction:
 Tapes are usually standardized at 20°C. Any variation above or
below this value will cause the tape to expand or contract, giving
rise to systematic errors.
 Temperature correction Ct = K L ∆t
 where;
 K= Coefficient of expansion
 For steel, K = 11.2 × 10–6
per °C
 For invar, K = 0.5 × 10–6
per °C
 L = measured length (m)
 ∆t = (tm –to)
difference between the measured and standard temperatures
The sign of the correction takes the sign of (tm –to).

11. 2. Tension Correction:
 Generally the tape is used under standard tension, in which
case there is no correction. It may, however, be necessary in
certain instances to apply a tension greater than standard.
From Hooke’s law:
 stress = strain × a constant
 This constant is the same for a given material and is called the
modulus of elasticity (E). Since strain is a non-dimensional
quantity, E has the same dimensions as stress, i.e. N/mm2
:

12. Tension Correction
 ∆T is normally the total stress acting on the cross-section, but
as the tape would be standardized under tension, ∆T in this
case is the amount of stress greater than standard. Therefore
∆T is the difference between field and standard tension. This
value may be measured in the field in kilograms and should be
converted to newtons (N) for compatibility with the other
units used in the formula, i.e. 1 kg = 9.80665 N.
 Where;
 E is modulus of elasticity in N/mm ;
 A is cross-sectional area of the tape in mm ; L is measured length
in m;
 ∆T = Tm –To
The sign of the correction takes the sign of (Tm –To).

13. 3. Sag Correction:
 When a tape is suspended between two measuring
heads, A and B, both at the same level, the shape it
takes up is a catenary.

14. 4 Cases: Quiz- How…??
If the tape is standardized and used on the flat,
no sag correction is required.
If the tape is standardized on flat and used on
the catenary, than measured length will be
greater than the actual length due to sag, the
negative sag correction is required.

2
2
2
32
2424 T
LW
T
Lw
Cs ==

15. Sag Correction
 Where;
 W2
=w2
L2
 w = weight of tape per unit length
 W = weight of tape between supports
 L = Length of tape between supports
 T = Tension applied
The above equation apply only to tapes standardized on the
flat and are always negative.
2
2
2
32
2424 T
LW
T
Lw
Cs ==

16.  When a tape is standardized in catenary, i.e. it records the
horizontal distance when hanging in sag, no correction is
necessary provided the applied tension, say TA, equals the
standard tension Ts.
 If tension TA exceed the standard, then a sag correction is
necessary for the excess tension (TA – Ts) and
 In this case the correction will be positive and vice versa.
Sag Correction due to error in applied tension






−= 22
32
11
24 As
s
TT
Lw
C

17.  If the difference in height of the two measuring heads is h, the
slope distance L and the horizontal equivalent D, then by
Pythagoras Theorem:
 Prior to the use of pocket calculators the following alternative
approach was generally used, due to the tedium of obtaining
square roots.
 On the relatively short lines involved in taping, the first term –
h2
/2L will generally suffice.
4. Slope Correction:

18. Slope Correction
 Alternatively if the vertical angle of the slope of the ground is
measured then:
 The sign of this correction is always negative.

19. 5. Altitude Correction:
 If the surveys are to be connected to the national mapping
system of a country, the distances will need to be reduced to
the common datum of that system, namely MSL.
 Alternatively, if the engineering scheme is of a local nature,
distances may be reduced to the mean level of the area.

20. Altitude Correction
 Consider Figure 3.11 in which a distance L is measured in a plane
situated at a height H above MSL.
 As H is negligible compared with R in the denominator.
 The correction is negative for surface work
but may be positive for tunneling or mining
work below MSL.

21. WORKED EXAMPLES