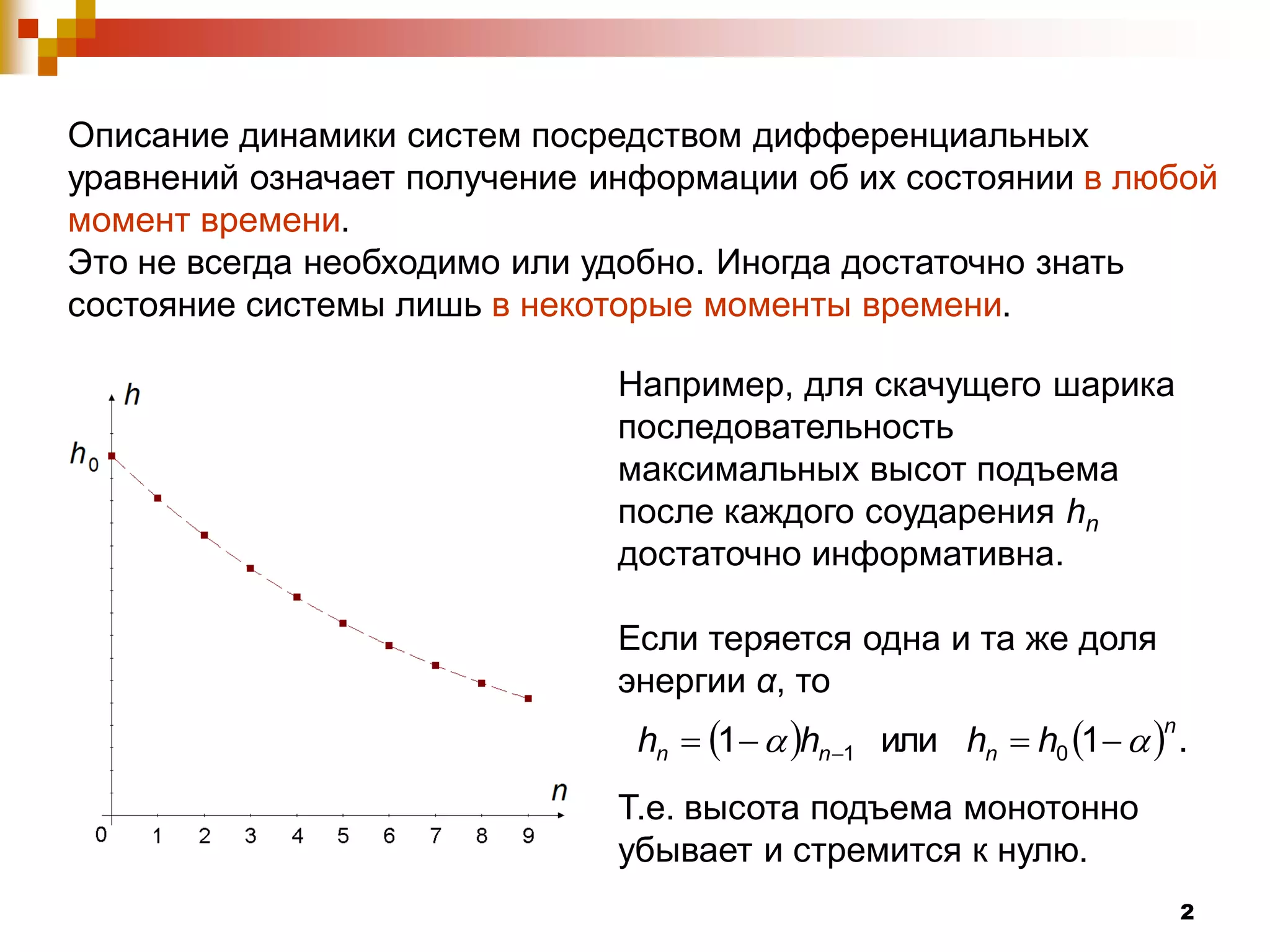
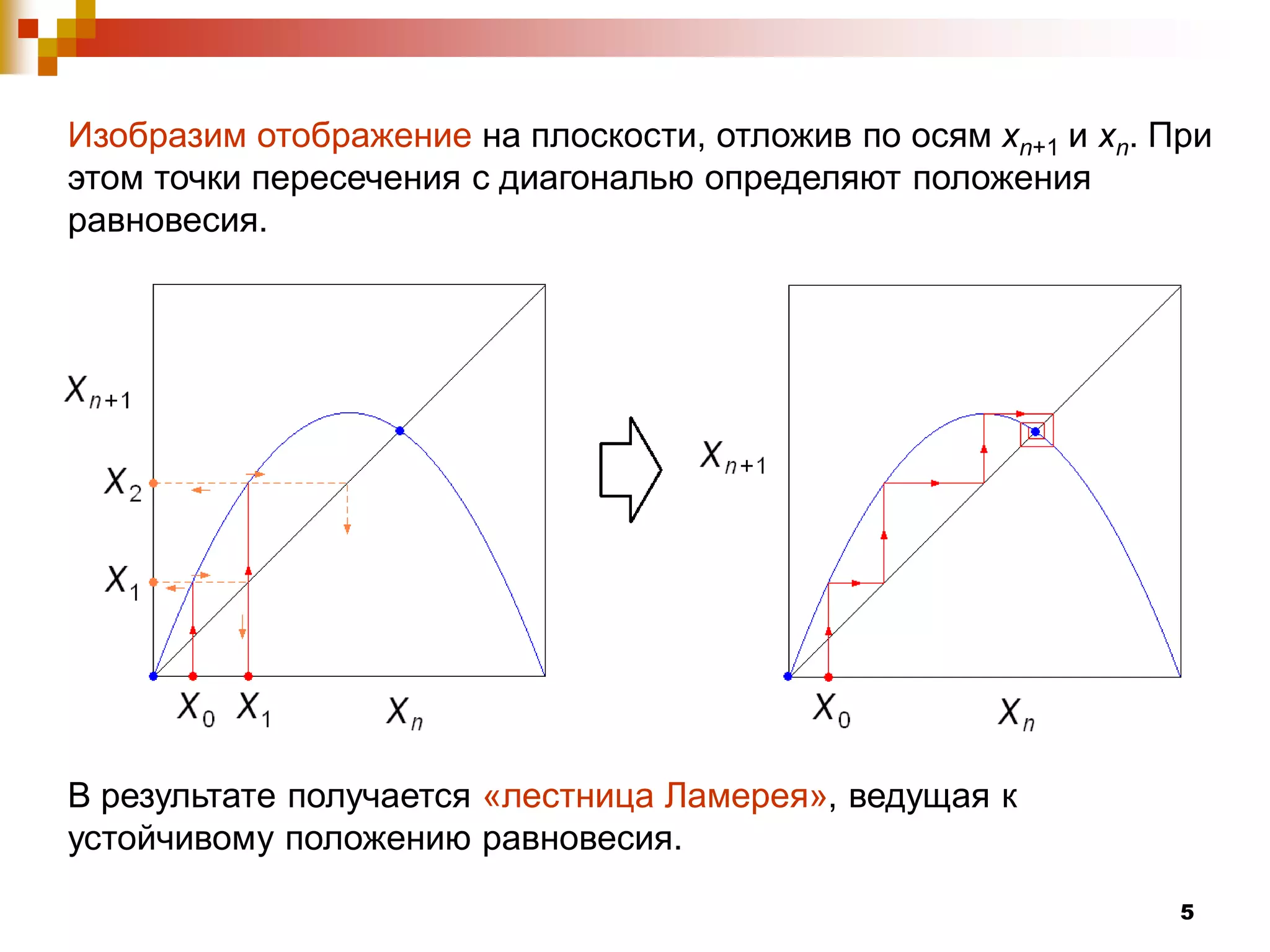
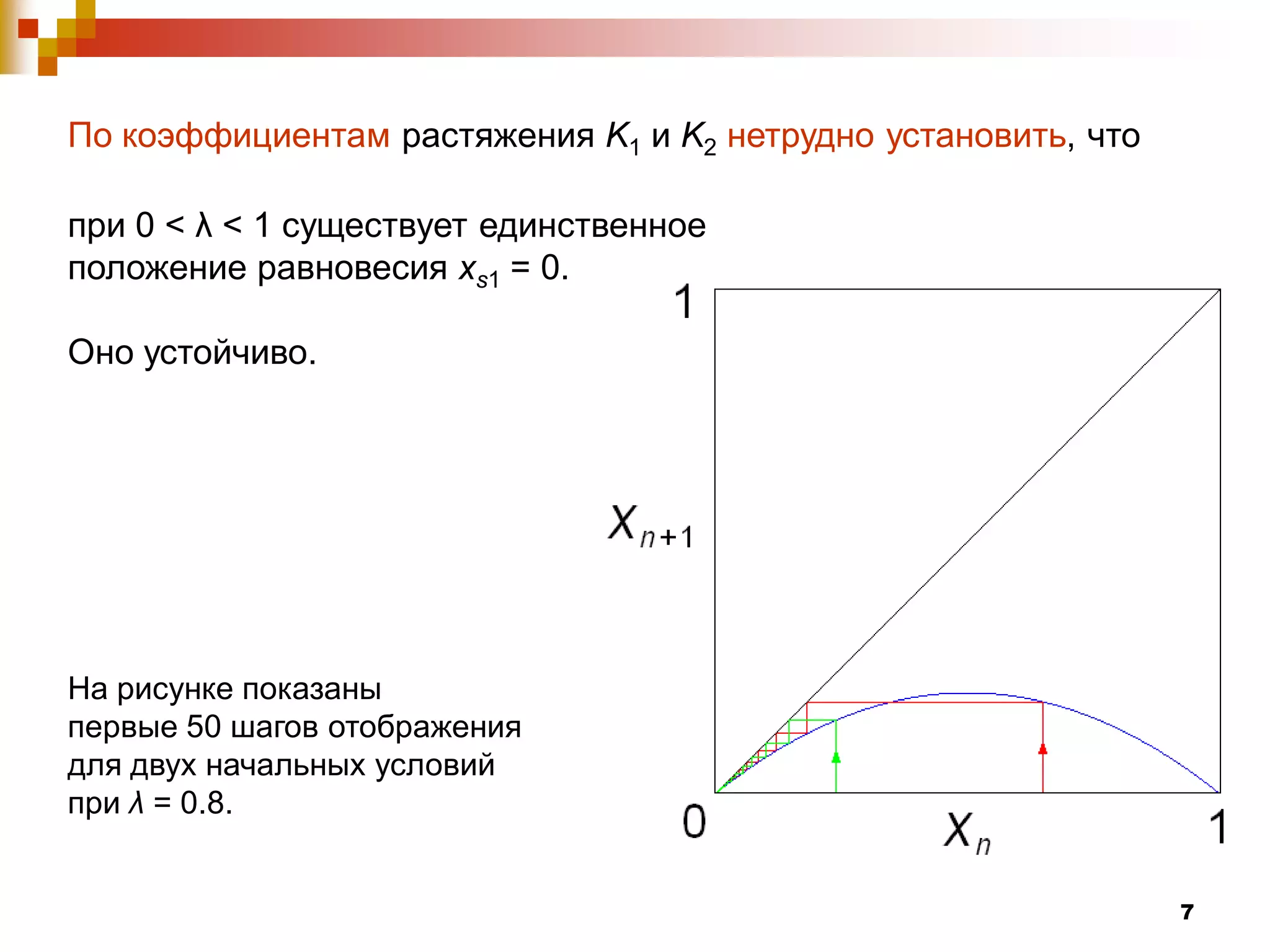
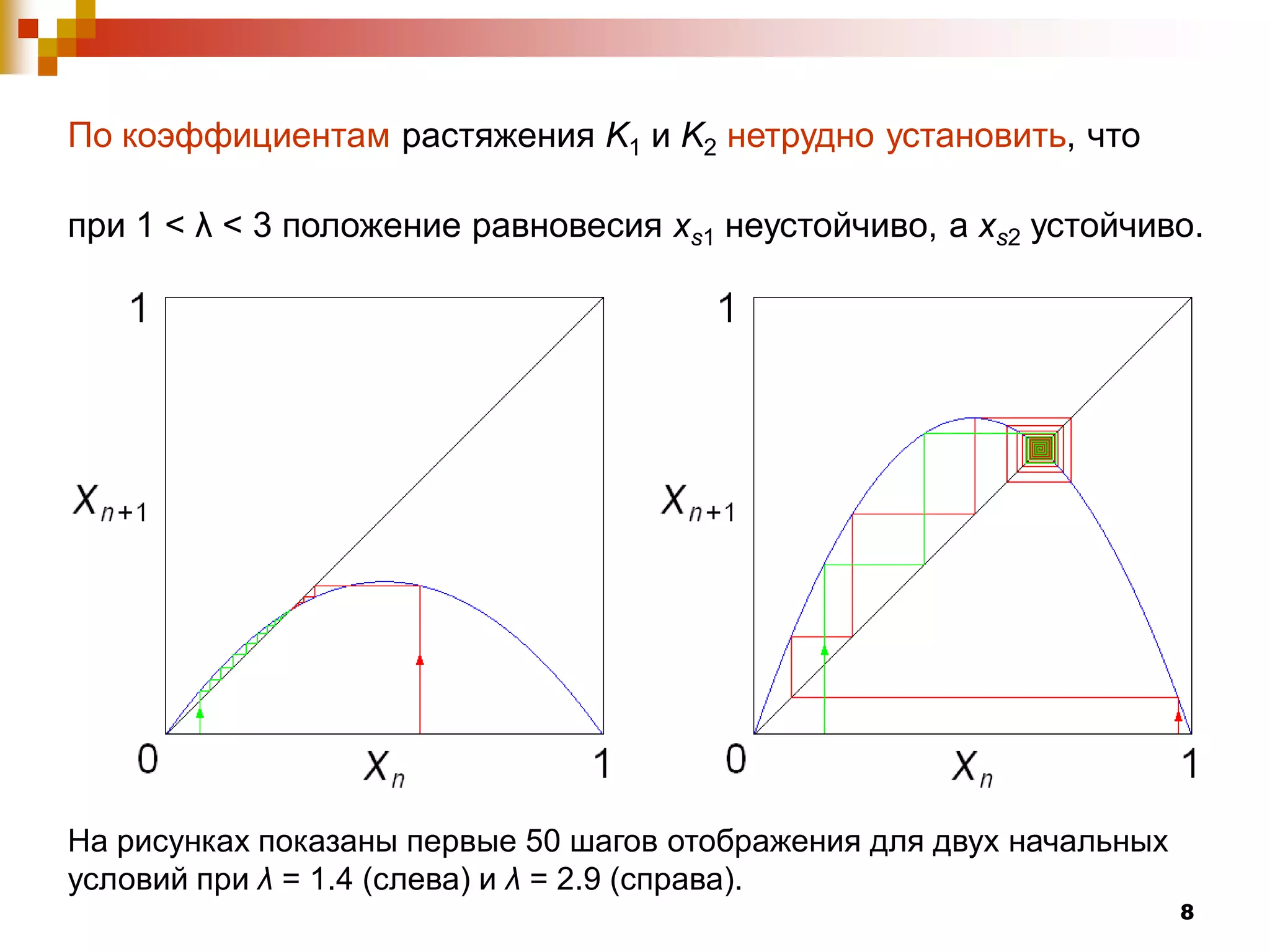
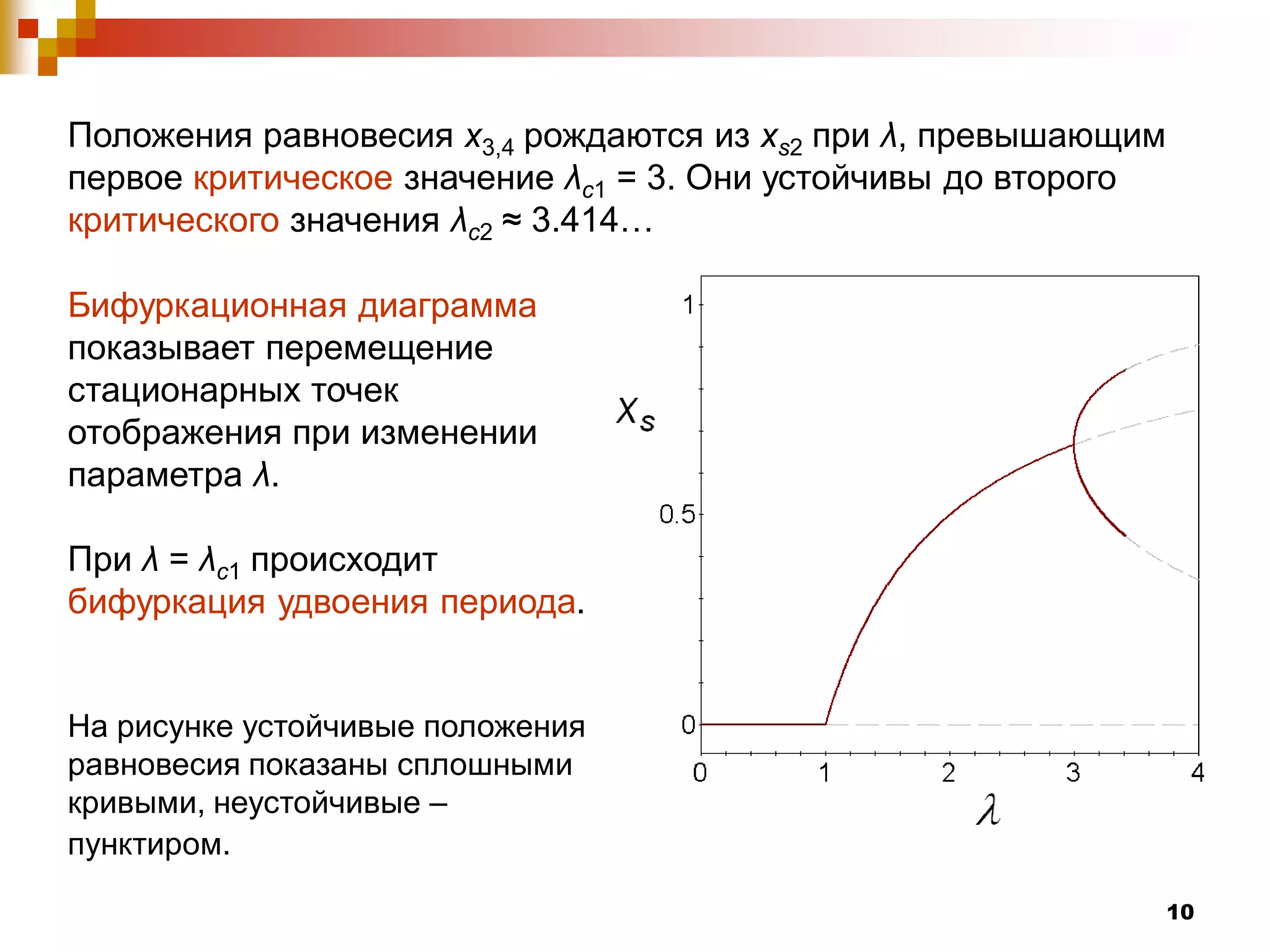
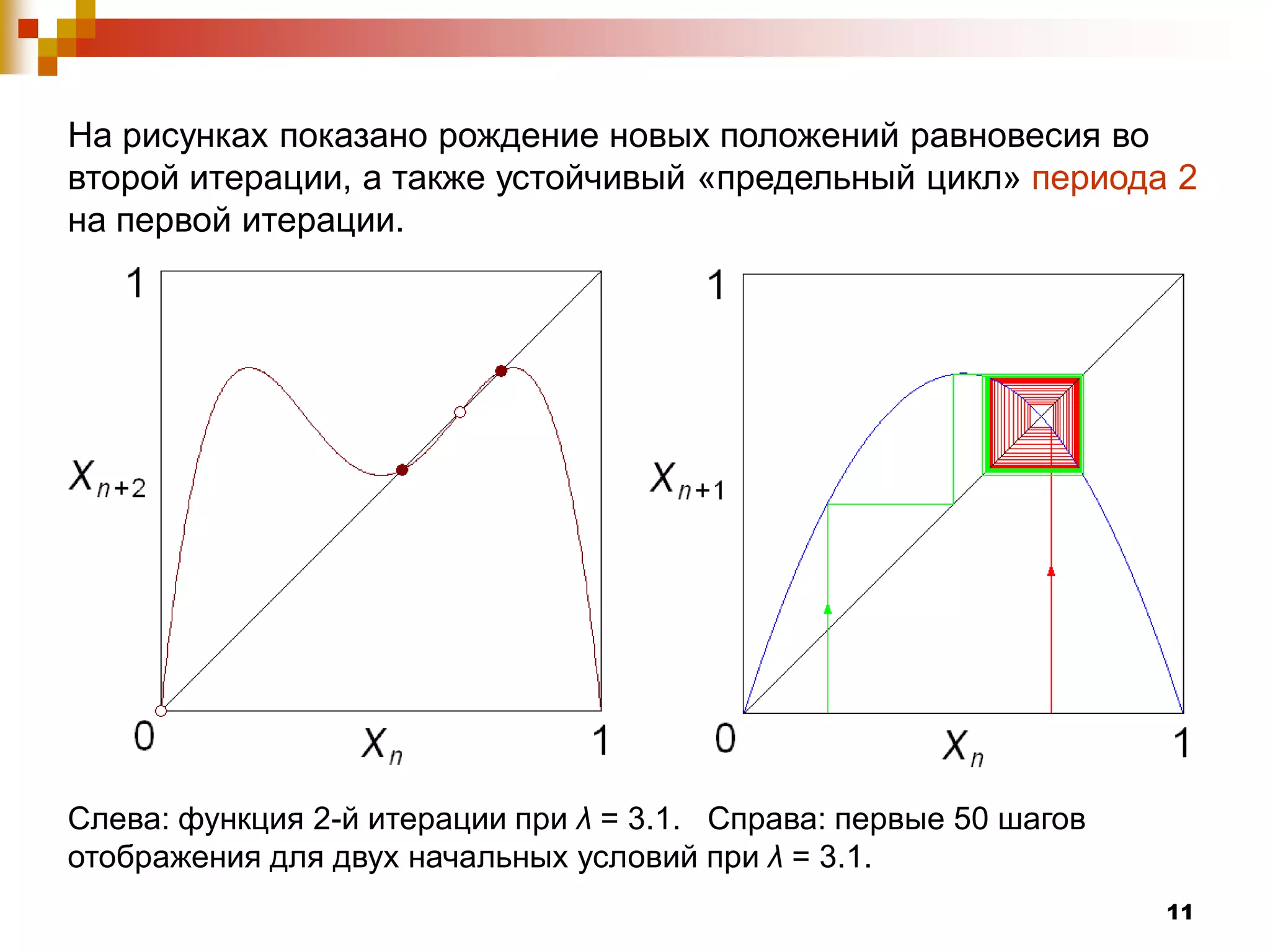
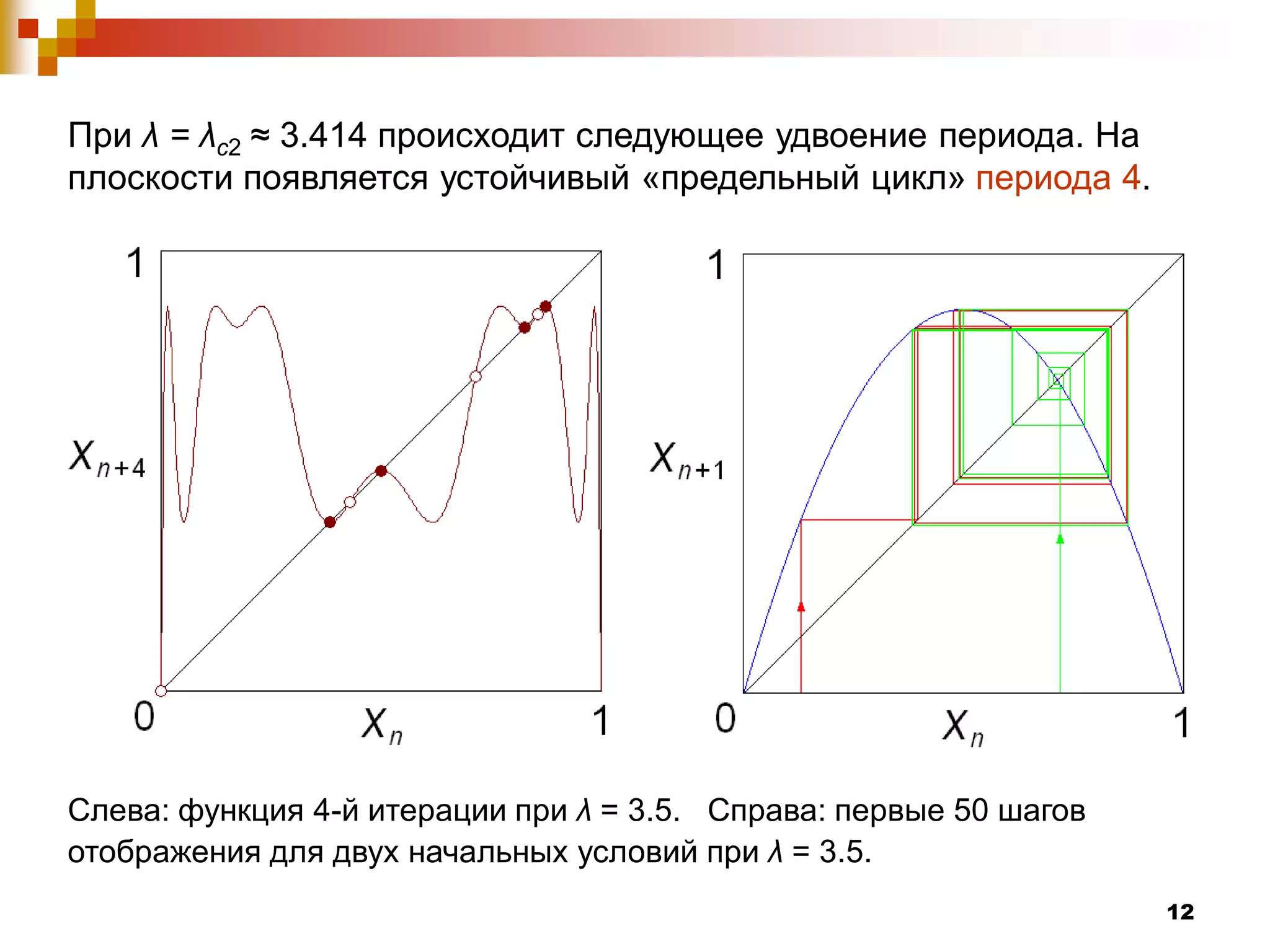
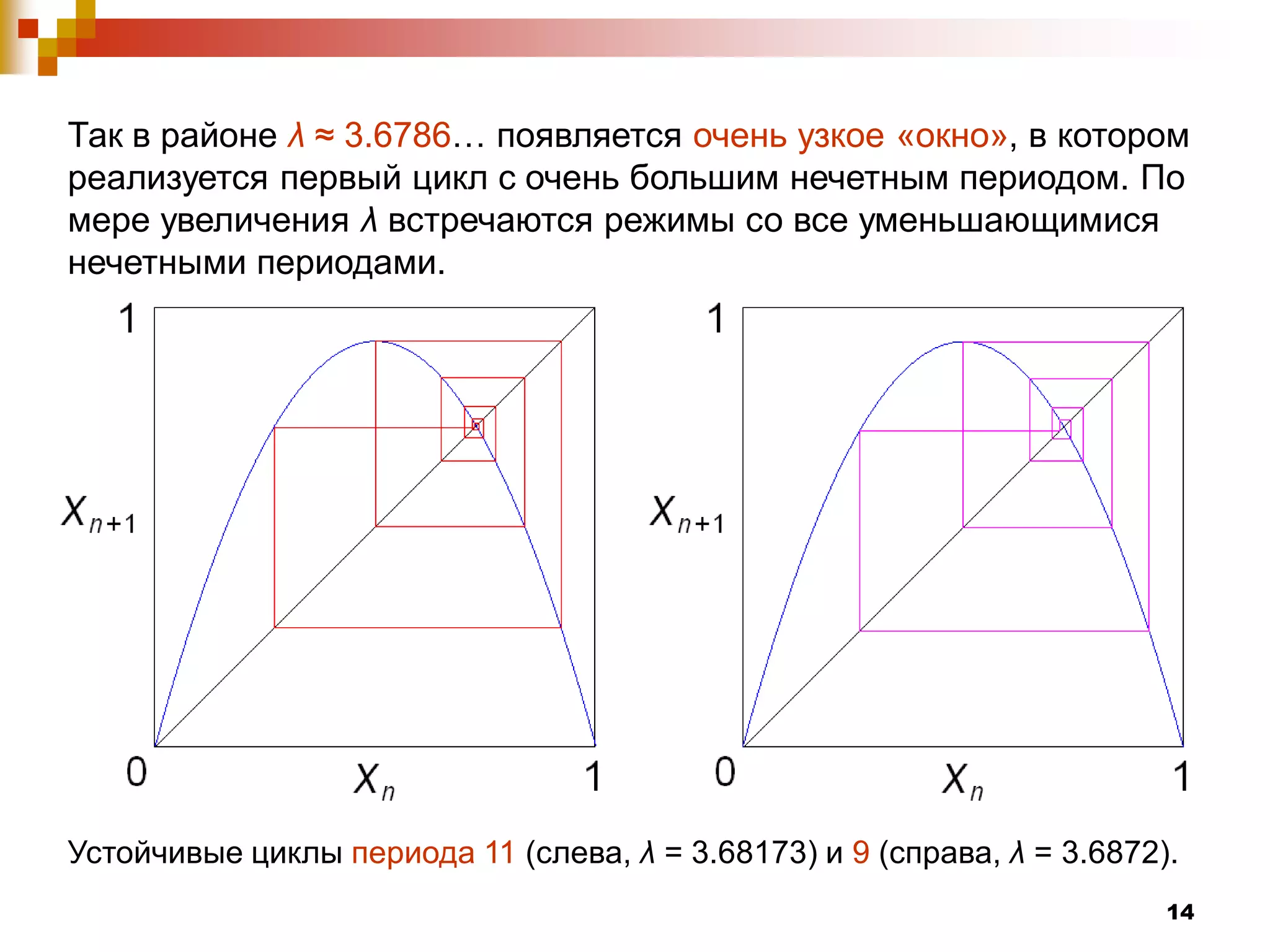
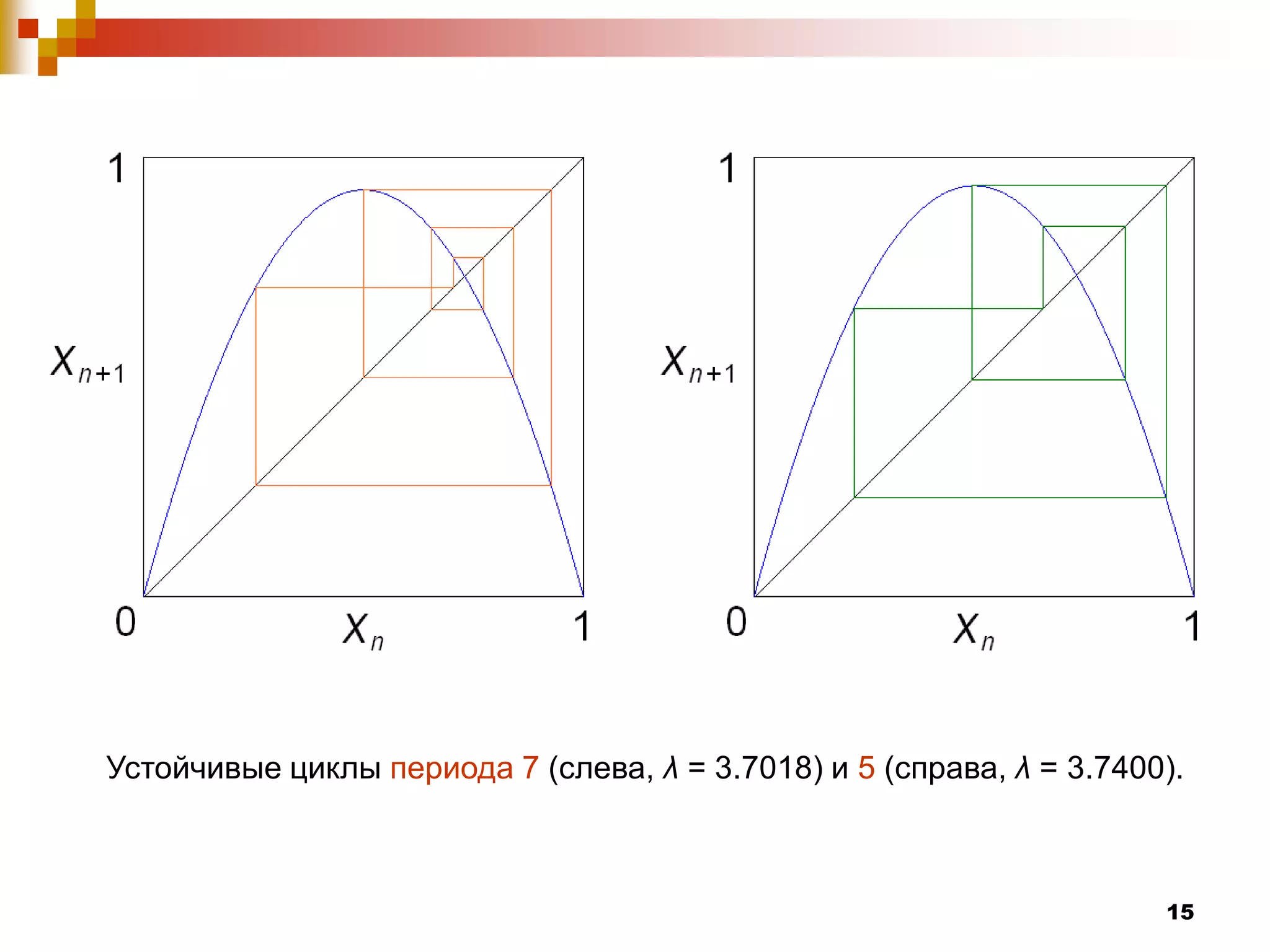
Документ посвящен изучению систем с дискретным временем и их динамическому поведению, которое описывается с помощью рекуррентных соотношений. Рассматриваются различные виды отображений, включая отображение Фейгенбаума, а также условия возникновения устойчивых и неустойчивых равновесий. Авторы демонстрируют сложные явления, такие как бифуркации и хаос, которые возникают при изменении параметра системы λ.

1. Лекция 6
Системы с дискретным
временем. Отображения
Малышев А.И.
Физический факультет ННГУ им. Н.И.Лобачевского

2. Описание динамики систем посредством дифференциальных
уравнений означает получение информации об их состоянии в любой
момент времени.
Это не всегда необходимо или удобно. Иногда достаточно знать
состояние системы лишь в некоторые моменты времени.
Например, для скачущего шарика
последовательность
максимальных высот подъема
после каждого соударения hn
достаточно информативна.
Если теряется одна и та же доля
энергии α, то
hn  1   hn 1 или hn  h0 1    .
n
Т.е. высота подъема монотонно
убывает и стремится к нулю.
2

3. Рекуррентное соотношение, связывающее два значения некоторой
динамической переменной х на n-ом и (n+1)-ом шагах, называется
отображением.
Отображение в общем виде: xn 1  f xn .
Выбор «шага» отображения диктуется условиями задачи.
Так в случае периодической по времени внешней силы логичный
«шаг» отображения – ее период. В примере со скачущим шариком
«шаг» определяется условием достижения максимальной высоты,
временные же промежутки не постоянны.
Необходимый набор данных мы получаем лишь в определенные
моменты, отделенные друг от друга интервалами конечной величины:
такие динамические системы называются системами с дискретным
временем.
3

4. Итак, начнем с изучения положений равновесия отображений.
Для их нахождения необходимо решить уравнение x  f x . Его
корни xs – стационарные точки отображения.
Выясним их устойчивость. При бесконечно малом отклонении от xs на
n-м шаге δxn на следующем шаге будет δxn+1 , причем
xn 1  K  xn ,
df
где K  – параметр растяжения.
dx x  x
s
Заметим:
 если K > 1, то |δxn+1| > |δxn|, т.е. вблизи x = xs траектории
разбегаются, т.е. положение равновесия неустойчиво;
 если K < 1, то любая близкая к x = xs траектория асимптотически
приближается к ней, т.е. положение равновесия устойчиво.
4

5. Изобразим отображение на плоскости, отложив по осям xn+1 и xn. При
этом точки пересечения с диагональю определяют положения
равновесия.
В результате получается «лестница Ламерея», ведущая к
устойчивому положению равновесия.
5

6. Отображение Фейгенбаума
Рассмотрим подробнее поведение системы, описываемой
отображением вида
xn 1  xn 1  xn .
Здесь λ > 0 – некоторый параметр задачи, а xn  0,1.
Отображение было предложено Фейгенбаумом для анализа
«логистической модели», описывающей эволюцию биологического
вида на ограниченной территории.
Положения равновесия:
 x s1  0,

x  x 1  x   
 x s 2  1  1 , при   1.

Для них K1  , K 2  2   .
6

7. По коэффициентам растяжения K1 и K2 нетрудно установить, что
при 0 < λ < 1 существует единственное
положение равновесия xs1 = 0.
Оно устойчиво.
На рисунке показаны
первые 50 шагов отображения
для двух начальных условий
при λ = 0.8.
7

8. По коэффициентам растяжения K1 и K2 нетрудно установить, что
при 1 < λ < 3 положение равновесия xs1 неустойчиво, а xs2 устойчиво.
На рисунках показаны первые 50 шагов отображения для двух начальных
условий при λ = 1.4 (слева) и λ = 2.9 (справа).
8

9. По коэффициентам растяжения K1 и K2 нетрудно установить, что
при λ > 3 оба положения равновесия неустойчивы.
Каково же тогда поведение системы?
Изучим вторую итерацию, т.е. связь между xn и xn+2:
x n  2  x n 1 1  x n 1   2 x n 1  x n 1  x n 1  x n .
Найдем положения равновесия:

 x1  x s1,

x  2 x 1  x 1  x 1  x   x 2  xs 2 ,

x 3,4 
  1   1  3 .

 2
Точки x3,4 рождаются из xs2 при λ > 3.
9

10. Положения равновесия x3,4 рождаются из xs2 при λ, превышающим
первое критическое значение λс1 = 3. Они устойчивы до второго
критического значения λс2 ≈ 3.414…
Бифуркационная диаграмма
показывает перемещение
стационарных точек
отображения при изменении
параметра λ.
При λ = λс1 происходит
бифуркация удвоения периода.
На рисунке устойчивые положения
равновесия показаны сплошными
кривыми, неустойчивые –
пунктиром.
10

11. На рисунках показано рождение новых положений равновесия во
второй итерации, а также устойчивый «предельный цикл» периода 2
на первой итерации.
Слева: функция 2-й итерации при λ = 3.1. Справа: первые 50 шагов
отображения для двух начальных условий при λ = 3.1.
11

12. При λ = λс2 ≈ 3.414 происходит следующее удвоение периода. На
плоскости появляется устойчивый «предельный цикл» периода 4.
Слева: функция 4-й итерации при λ = 3.5. Справа: первые 50 шагов
отображения для двух начальных условий при λ = 3.5.
12

13. Удвоения периода продолжаются и при последующем росте λ.
Фейгенбаумом была установлена зависимость появления новых
критических чисел λсk:
  ck 1
lim ck 1  ,
k  
ck  ck 1 
где δ ≈ 4.6692…
Критические числа образуют последовательность, сходящуюся к
точке накопления λ∞ ≈ 3.56994… (период через удвоения вырастает
до бесконечности).
При λ > λ∞ поведение становится апериодическим и демонстрирует
хаос,…
…однако при дальнейшем увеличении λ наблюдаются и узкие
«окна», в которых наблюдаются устойчивые периодические решения,
причем с нечетным периодом!
13

14. Так в районе λ ≈ 3.6786… появляется очень узкое «окно», в котором
реализуется первый цикл с очень большим нечетным периодом. По
мере увеличения λ встречаются режимы со все уменьшающимися
нечетными периодами.
Устойчивые циклы периода 11 (слева, λ = 3.68173) и 9 (справа, λ = 3.6872).
14

15. Устойчивые циклы периода 7 (слева, λ = 3.7018) и 5 (справа, λ = 3.7400).
15

16. Последним возникает «окно», отвечающее периоду 3, за которым
следует область хаоса.
Устойчивый цикл периода 3 (слева, λ = 3.8320) и разбегание двух близких
начальных условий в области хаоса (справа, λ = 3.9, показаны первые 7
шагов отображения).
16

17. Задания по теме
1. Найти значение параметра λ, при котором произойдет первое
удвоение периода в системе:
x n 1  x n 1  x n .
2
2. Показать, что отображение x n 1  x n  a x n  2 можно
использовать для вычисления квадратного корня из числа а.
Можно ли для тех же целей использовать отображение
x n 1  a x n ?
17