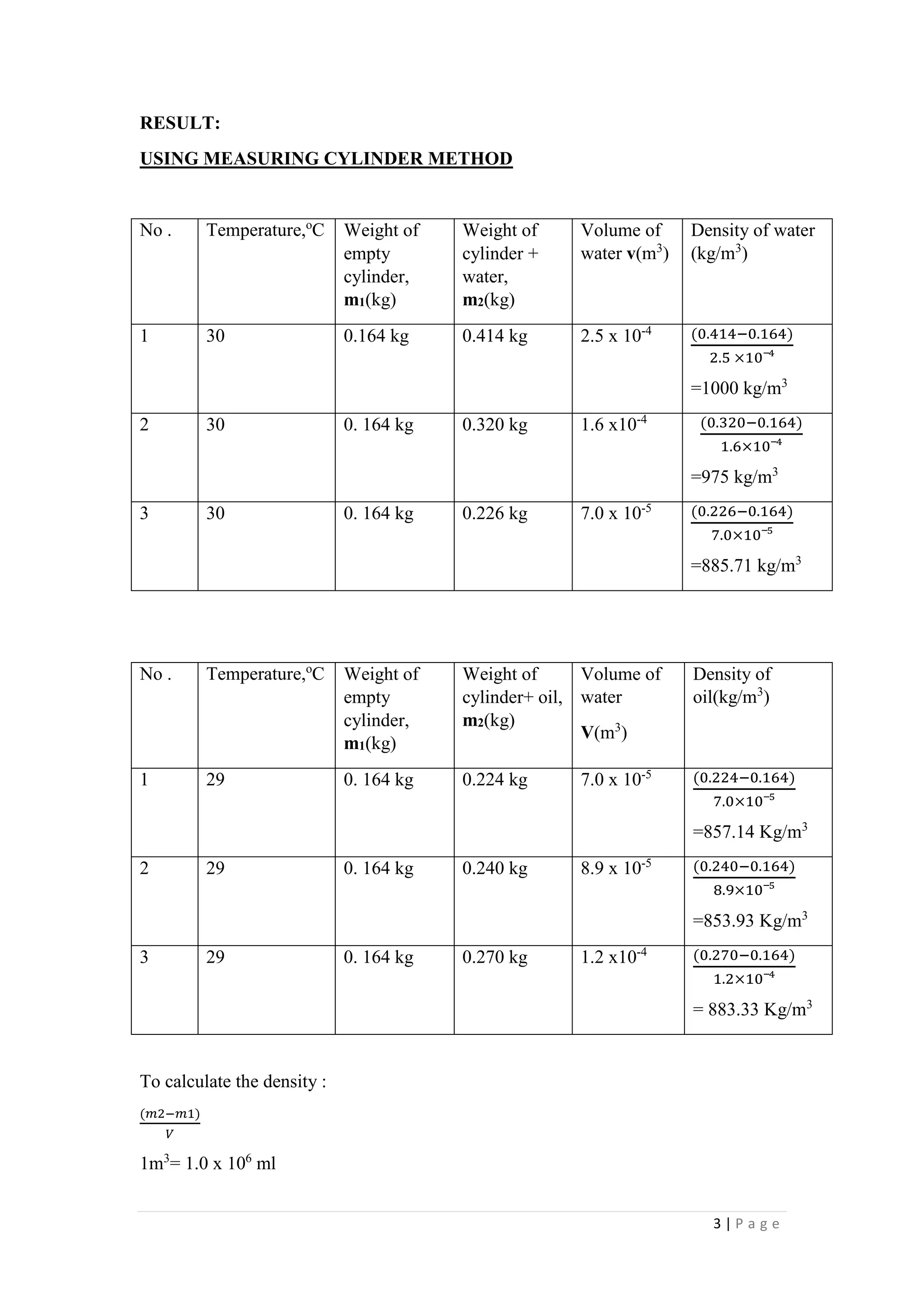
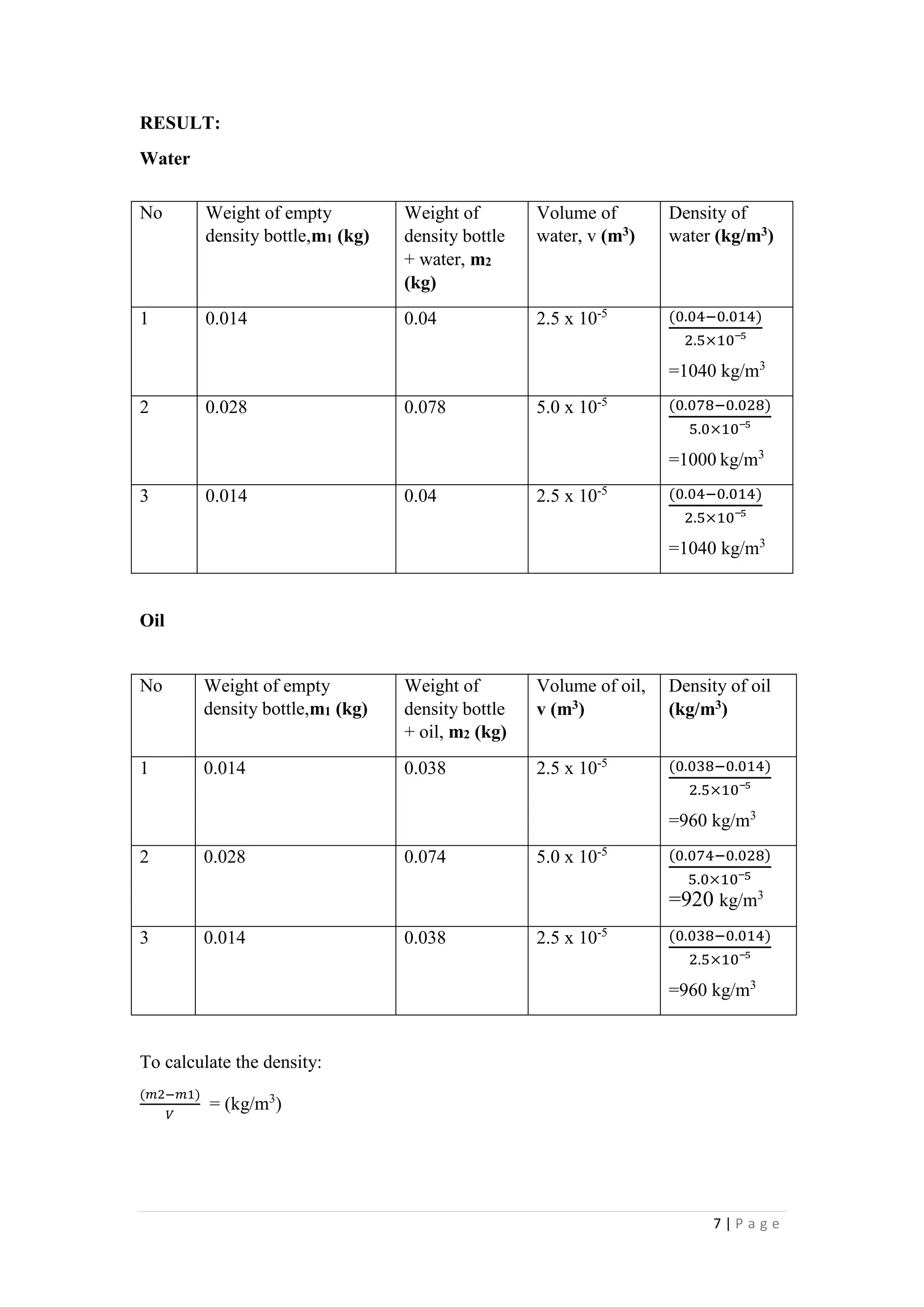
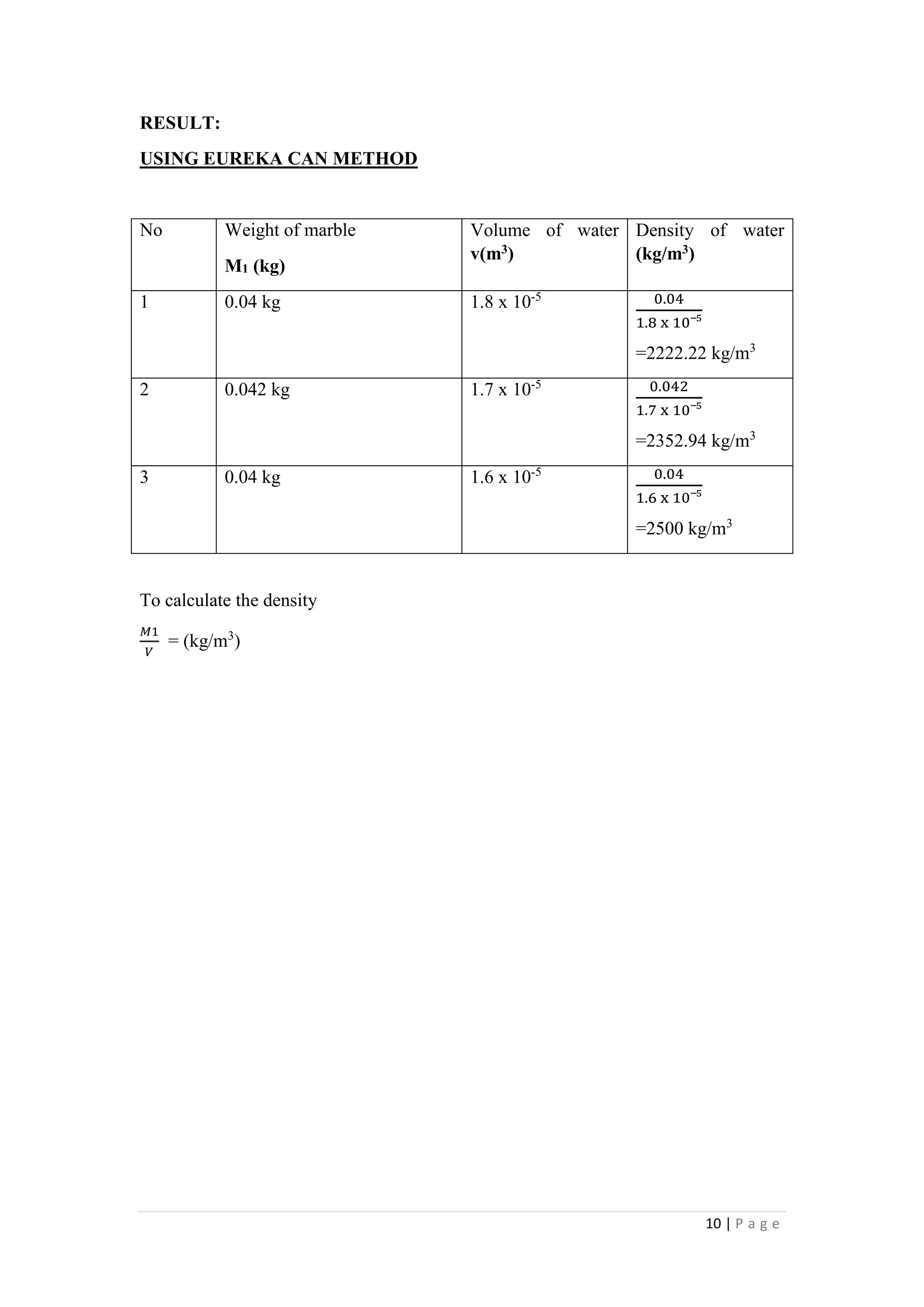
1. The document describes four experiments to determine the density of water and oil using different methods: a measuring cylinder, density bottle, Eureka can, and hydrometer. 2. The densities measured ranged from 885-1000 kg/m3 for water and 857-883 kg/m3 for oil depending on the method. The density bottle was deemed the most accurate method. 3. Specific gravities were also calculated from the density measurements, with water having a specific gravity of 0.953-1.027 and oil 0.865-0.947.

1. 1 | P a g e
THEORY
Mass density is defined as the mass of material per unit volume (kg/m3).
Therefore to determine of a liquid it is necessary to determine the mass of a known
volume of liquid.
Specific gravity, also called relative density of a substance may be defined as the
ratio of its mass density to the mass density of water taken at atmospheric pressure at
4 degree.
EXPERIMENT 1.1 : To determine the density of fluid using measuring cylinder.
OBJECTIVE : To determine the density of water and oil.
APPARATUS :
Measuring cylinder
Balance (manual or automatic)
Water Thermometer
Oil

2. 2 | P a g e
PROCEDURE
1. Weight an empty cylinder and record mass.
2. Fill with water at a certain volume, read and record volume as accurately as
possible .
3. Weight the cylinder with water and record the mass.
4. Measure the temperature of water.
5. Repeat step 1 - 3 to take average.
6. Repeat step 1 - 4 with oil.

3. 3 | P a g e
RESULT:
USING MEASURING CYLINDER METHOD
No . Temperature,o
C Weight of
empty
cylinder,
m1(kg)
Weight of
cylinder +
water,
m2(kg)
Volume of
water v(m3
)
Density of water
(kg/m3
)
1 30 0.164 kg 0.414 kg 2.5 x 10-4 (0.414−0.164)
2.5 ×10‾⁴
=1000 kg/m3
2 30 0. 164 kg 0.320 kg 1.6 x10-4 (0.320−0.164)
1.6×10‾⁴
=975 kg/m3
3 30 0. 164 kg 0.226 kg 7.0 x 10-5 (0.226−0.164)
7.0×10‾⁵
=885.71 kg/m3
No . Temperature,o
C Weight of
empty
cylinder,
m1(kg)
Weight of
cylinder+ oil,
m2(kg)
Volume of
water
V(m3
)
Density of
oil(kg/m3
)
1 29 0. 164 kg 0.224 kg 7.0 x 10-5 (0.224−0.164)
7.0×10‾⁵
=857.14 Kg/m3
2 29 0. 164 kg 0.240 kg 8.9 x 10-5 (0.240−0.164)
8.9×10‾⁵
=853.93 Kg/m3
3 29 0. 164 kg 0.270 kg 1.2 x10-4 (0.270−0.164)
1.2×10‾⁴
= 883.33 Kg/m3
To calculate the density :
(𝑚2−𝑚1)
𝑉
1m3
= 1.0 x 106
ml

4. 4 | P a g e
EXPERIMENT 1.2: To determine the density of fluid using density bottle method
OBJECTIVE : To determine the density of water and oil
APPARATUS :
Density bottle
Oil
Balance Water

5. 5 | P a g e
PROCEDURE:
1) Dry 25ml density bottle and stopper
2) Weight the density bottle and stopper and record mass, m1
3) Fill the density bottle with water until it is full and put the stopper on top of it,
take the volume base on the density bottle volume, v
4) Carefully dry the outside of the bottle with a cloth or Tissue paper and remove
any excess water from the stopper such that the liquid in the hole is level with
the top of the stopper. Weight the bottle with water and record the mass, m2
5) Repeat procedure 1-3, by using different volume of density bottle to take
average.
6) Repeat procedure 1-4 with oil.

6. 6 | P a g e

7. 7 | P a g e
RESULT:
Water
Oil
To calculate the density:
(𝑚2−𝑚1)
𝑉
= (kg/m3
)
No Weight of empty
density bottle,m1 (kg)
Weight of
density bottle
+ water, m2
(kg)
Volume of
water, v (m3)
Density of
water (kg/m3)
1 0.014 0.04 2.5 x 10-5 (0.04−0.014)
2.5×10‾⁵
=1040 kg/m3
2 0.028 0.078 5.0 x 10-5 (0.078−0.028)
5.0×10‾⁵
=1000 kg/m3
3 0.014 0.04 2.5 x 10-5 (0.04−0.014)
2.5×10‾⁵
=1040 kg/m3
No Weight of empty
density bottle,m1 (kg)
Weight of
density bottle
+ oil, m2 (kg)
Volume of oil,
v (m3)
Density of oil
(kg/m3)
1 0.014 0.038 2.5 x 10-5 (0.038−0.014)
2.5×10‾⁵
=960 kg/m3
2 0.028 0.074 5.0 x 10-5 (0.074−0.028)
5.0×10‾5
=920 kg/m3
3 0.014 0.038 2.5 x 10-5 (0.038−0.014)
2.5×10‾⁵
=960 kg/m3

8. 8 | P a g e
EXPERIMENT 1.3: To determine the density of solid by using eureka can.
OBJECTIVE : To determine the density of water and oil.
APPARATUS :
Beaker Eureka can
Measuring cylinder
Glass marble
Water

9. 9 | P a g e
PROCEDURE
1. Weight four marble and record a mass.
2. Fill in the eureka can till the funnel with water.
3. Put the marble in the eureka can. Use the beaker collect the water come out
from the funnel. Measure the volume of water by using measuring cylinder.
4. Repeat step 1 - 3 to take average.

10. 10 | P a g e
RESULT:
USING EUREKA CAN METHOD
No Weight of marble
M1 (kg)
Volume of water
v(m3)
Density of water
(kg/m3)
1 0.04 kg 1.8 x 10-5 0.04
1.8 x 10‾⁵
=2222.22 kg/m3
2 0.042 kg 1.7 x 10-5 0.042
1.7 x 10‾⁵
=2352.94 kg/m3
3 0.04 kg 1.6 x 10-5 0.04
1.6 x 10‾⁵
=2500 kg/m3
To calculate the density
𝑀1
𝑉
= (kg/m3
)

11. 11 | P a g e
EXPERIMENT 1.4 : To determine specific gravity using hydrometer.
OBJECTIVE : To determine the density of water and oil.
APPARATUS :
Water
Oil
Measuring cylinder 1000ml
Hydrometer

12. 12 | P a g e
PROCEDURE:
1. Fill 3/4 full of 1000 measuring cylinder with water.
2. Properly put hydrometer in the cylinder.
3. Take reading from hydrometer. Make sure the hydrometer no touch the
cylinder while reading taken.
4. Repeat procedure 1-3 but replace water and oil.
RESULT:
Using hydrometer
fluid specific gravity
water 0.950
oil 0.850
Experiment 1.4.1: Calculate specific gravity from experiment 1.1 and 1.2
Experiment Water density (kg/m3
) Specific gravity
1.1: using measuring
cylinder
953.57 0.953
1.2: using density bottle 1026.67 1.027
Specific gravity, Gs =water density/water density
Experiment Oil density (kg/m3) Specific gravity
1.1: using measuring
cylinder
864.8 0.865
1.2: using density bottle 946.67 0.947
Specific gravity, Gs =oil density/water density

13. 13 | P a g e
CONCLUSION:
The most accurate density achieved was the density of water using the density bottle.
The true density of water is 1000 kg/m3
. The second most accurate density achieved
was the density of water using a measuring beaker. The least accurate density
achieved was the density of water using a Eureka can. The most accurate density was
the density bottle because the density bottle is built to have an exact volume of water,
removing human error in reading, which is done using the measuring beaker of
Eureka can.
DISCUSSION:
There is not much difference between the theoretical and experimental result of water
density. This is closed but not exact. There is a few factor that can cause the
difference between the theoretical and experimental result such as the temperature
effects, mass and others. Density varies with temperature. Over the range of
temperatures that people encounter in everyday life, this variation is negligible for
many kinds of substances. It introduces another possible source of error, however,
because if you measure density at one temperature, your result may not be valid at
another. Moreover, the density of a gas varies widely with pressure and temperature,
so for a gas your result is only meaningful under specified conditions. The final
possible source of error in this experiment is mass. Typically, you can measure mass
with a scale or balance. However, the accuracy of your measurement will depend on
the kind of scale you use. A kitchen scale, for example, is probably less accurate than
a calibrated scale in a lab. But there is also human error in this experiment which is
the error when taking the reading.
Usually, our reference liquid is water, which has a density of 1 g/mL or 1 g/cm^3.
Because the density is directly related to the mass, the specific gravity can also be
determined from the ratios of the mass of the object to the mass of the water, or the
ratios of the weight of the object to the weight of water. The reason for the specific
gravity being dimensionless is to provide a global consistency between the U.S. and
Metric Systems, since various units for density may be used such as pounds per cubic
feet or grams per cubic centimeter, etc. Specific gravity varies with temperature and
pressure; reference and sample must be compared at the same temperature and
pressure or be corrected to a standard reference temperature and pressure. Substances
with a specific gravity of 1 are neutrally buoyant in water. Those with SG greater than
1 are denser than water and will, disregarding surface tension effects, sink in it. Those
with an SG less than 1 are less dense than water and will float on it. In scientific work,
the relationship of mass to volume is usually expressed directly in terms of the density
(mass per unit volume) of the substance under study. It is in industry where specific
gravity finds wide application, often for historical reasons.