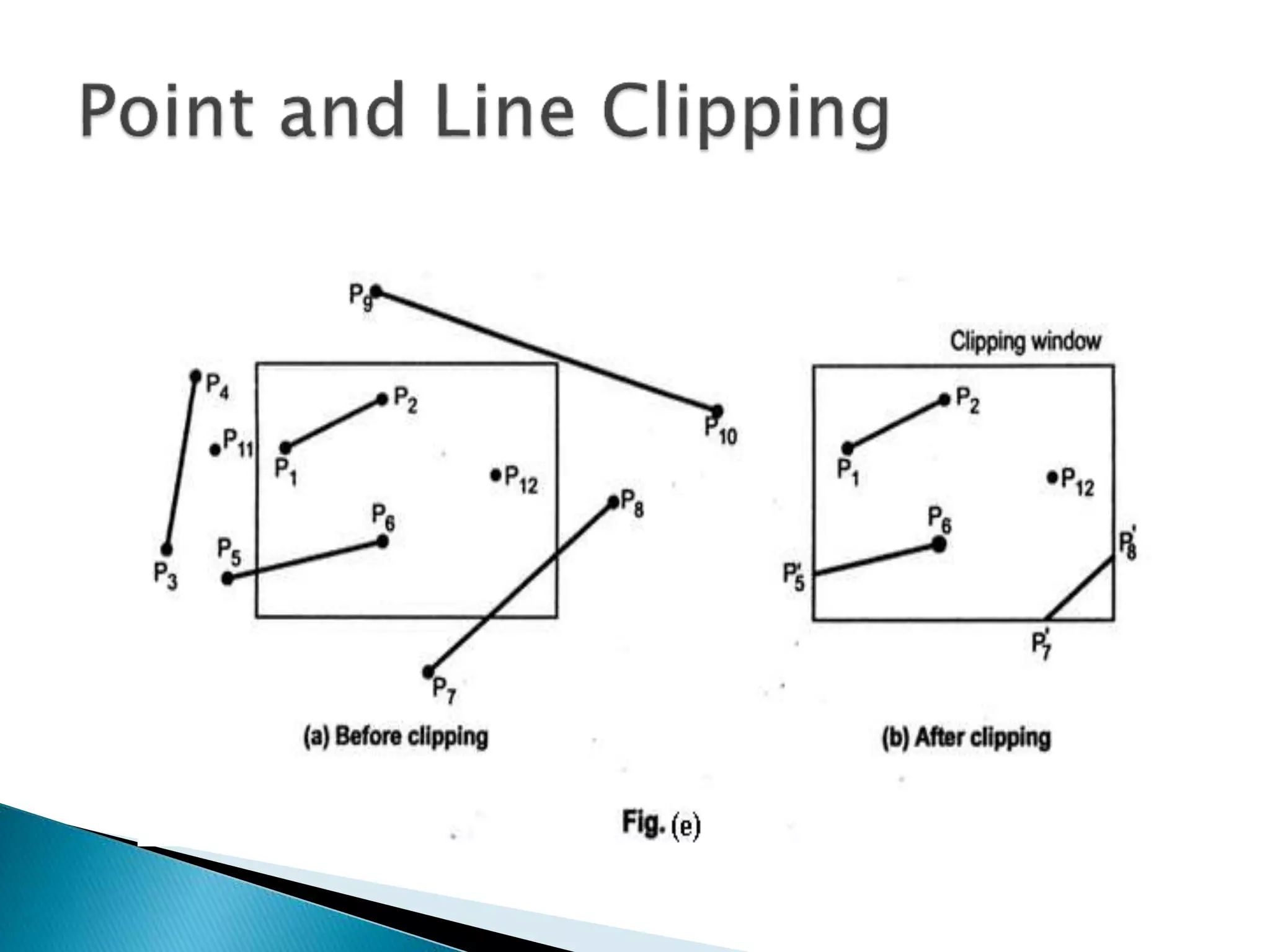
The document discusses window port and viewport clipping in computer graphics. It provides an example of finding the visible segment of a line between points P(60,140) and Q(220,40) within a specified window port range of (40,200) for x-values and (20,120) for y-values. The solution finds the intersection points of the line PQ with the boundaries of the window port to determine the visible portion P'Q' between points P'(92,120) and Q'(200,52.5).

1. Arvin Bera
(Lecturer CST KPC)
Arvin Bera
(Lecturer CST KPC)

2. 1. Window port and viewport
2. Point and Line clipping
3. Problems on clipping

3.  Window port : A world Co ordinate area selected
for display
 Viewport: This is a rectangular region of the
screen which is selected for displaying the object.

5.  Find the visible segment to be displayed in the viewport for
the line from P(60,140) to Q(220,40) in the Window port
having range (Wxmin,wxmax)=(40,200) and
(Wymin,Wymax)=(20,120)
 Soln.

6. From the figure we can see that ABCD is the window port
So to find out the visible portion of the line we need to find the
Intersection point of PQ and AB,PQ and BC
Equation of AB Y=120…………(i)
Equation of BC X=200…………(ii)
To find out the equation of PQ we need the value of m(tangent of PQ)
because the equation of any straight line is
(y-y1)=m(x-x1) where m=tangent=(y2-y1)/(x2-x1)
In case of PQ straight line P(x1,y1)(60,140) and Q(x2,y2)(220,40)
So the tangent is m=(40-140)/(220-60)=-0.625

7.  Equation of PQ is
Y-140=-0.625(x-60)  5x+8y=1420……….(iii)
Now we have to solve equation (i) and (iii) we will get
X=92,y=120 (Coordinate of P’)
Now we have to solve equation (ii) and (iii) we will get
X=200,y=52.5 ((Coordinate of Q’))(P’Q’ is visible portion)

8.  https://youtu.be/4GCM_pd4LGY
 https://youtu.be/k44p9pEG0HM

9. Thank you