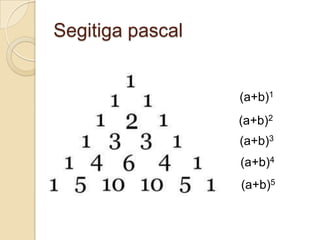
Dokumen tersebut membahas tentang teori dasar kemungkinan, termasuk rumus-rumus dan contoh soal untuk menghitung kemungkinan terjadinya suatu peristiwa. Secara khusus membahas tentang kemungkinan terjadinya satu peristiwa, dua peristiwa yang berdiri sendiri, dua peristiwa yang saling mempengaruhi, dan penggunaan rumus binomium dan segitiga Pascal dalam menghitung kemungkinan.

1. KEMUNGKINAN
Luisa Diana Handoyo, M.Si.

2. Dasar Teori Kemungkinan
1. Kemungkinan atas terjadinya sesuatu
yang diinginkan ialah = perbandingan
antara sesuatu yang diinginkan itu
terhadap keseluruhannya.
Formula
K = kemungkinan
K(x) = besarnya kemungkinan untuk
mendapatkan x
x+y = jumlah keseluruhannya

3. Contoh
 Anton melempar sebuah dadu, berapa
kemungkinannya akan mendapatkan
angka 3 ?
 Jawab :
Kemungkinan mendapatkan angka 3

4. 2. Kemungkinan terjadinya dua peristiwa
atau lebih, yang masing-masing berdiri
sendiri ialah = hasil perkalian dari
besarnya kemungkinan untuk peristiwa-
peristiwa tersebut.
Formula :

5. Contoh
 Marto melakukan tos dengan 2 uang logam bersama-
sama (satu di tangan kiri dan satu di tangan kanan),
berapa kemungkinannya akan memperoleh kepala
pada kedua uang logam tersebut ?
 Jawab :
K(kepala) = ½
K(kepala + kepala) = ½ x ½ = ¼
artinya bahwa setiap 4 kali melakukan tos dengan 2
uang logam tersebut, kesempatan untuk
mendapatkan kepala pada dua uang logam itu adalah
satu kali saja.

6. 3. Kemungkinan terjadinya dua
peristiwa atau lebih, yang saling
mempengaruhi satu sama lain ialah =
jumlah dari besarnya kemungkinan
untuk peristiwa-peristiwa tersebut.
Formula :

7. Contoh
 Maria melakukan tos dengan 2 uang logam
bersamaan, berapa kemungkinannya akan
mendapatkan dua kepala atau dua ekor
pada kedua uang logam itu ?
 Jawab :
K(kepala) = ½
K(ekor) = ½
K(dua kepala) = ½ x ½ = ¼
K(dua ekor) = ½ x ½ = ¼
K(2 kepala atau 2 ekor) = ¼ + ¼ = ½

8. Penggunaan rumus binomium (a+b)n
a dan b merupakan kejadian yang
terpisah.
Contoh :
Kita melakukan tos dengan 3 uang
logam bersama sama. Berapa
kemungkinannya kita mendapatkan
satu kepala dan dua ekor pada ketiga
uang logam ?

9. Jawaban
Karena digunakan 3 uang logam maka n = 3
Kemungkinan mendapatkan kepala atau ekor
adalah sama yaitu ½.
Misalkan : a = kemungkinan mendapat kepala
(½)
b = kemungkinan mendapatkan ekor
(½)
Maka (a+b)3 = a3+ 3a2b+3ab2+b3
Sekarang kita masukkan perumpamaan di atas
ke dalam rumus, sehingga :
K (1 kepala, 2ekor) = 3ab2
= 3 (½)(½) 2
=⅜

10. Segitiga pascal
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5

11. Soal
1. Sepasang mempelai baru menginginkan 5 orang
anak. Berapakah kemungkinannya bahwa anak-
anak mereka akan terdiri dari :
a. 2 anak perempuan dan 3 laki-laki
b. 4 anak perempuan dan 1 laki-laki
c. Semua anak perempuan
d. Urutan tertentu : laki-laki,perempuan,laki-laki,
perempuan, laki-laki

12. 2. Suami isteri masing-masing normal tapi
heterozigot untuk albino ingin memiliki 4 orang
anak. Berapa kemungkinannya bahwa :
a. Semua anak akan normal
b. Seorang anak saja yang albino, 3 lainnya normal
c. Anak yang terakhir saja yang albino
3. Seorang kidal disebabkan oleh gen resesif r yang
homozigotik. Alelnya R menyebabkan orang
normal. Suami isteri masing-masing normal
namun heterozigotik untuk kidal ingin memiliki 6
orang anak. Berapakah kemungkinannya bahwa :
a. Semua anak kidal
b. Semua anak normal
c. Anak-anaknya normal, kecuali nomor 2 yang
kidal

13. 4. Dentinogenesis imperfecta adalah kelainan
pada gigi manusia yang membuat gigi
berwarna kecoklatan dan mahkota gigi masuk
ke dalam gusi. Kelainan ini disebabkan oleh
gen dominan D, sedang alelnya d menentukan
gigi normal. Seorang lelaki penderita kelainan
ini namun heterozigot menikah dengan
seorang wanita normal. Mereka memiliki 3
orang anak. Berapakah kemungkinannya :
a. Semua anak menderita kelainan tsb.
b. Semua anak bergigi normal
c. Anak pertama menderita kelainan, sedang 2
anak lainnya tidak
d. Salah seorang diantara anak-anak itu
menderita kelainan ini.