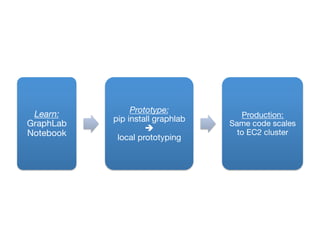
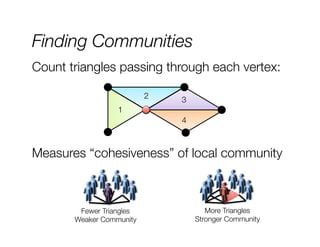
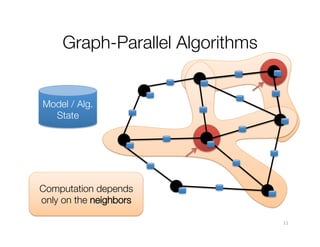
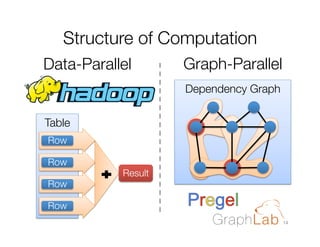
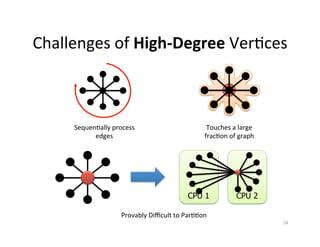
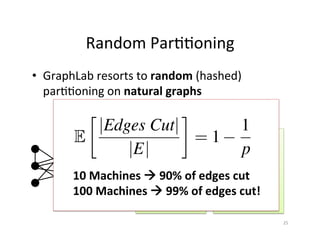
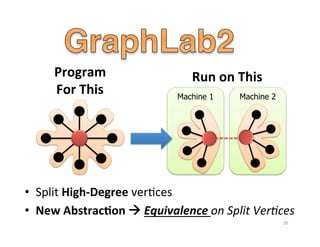
The document discusses machine learning techniques for graphs and graph-parallel computing. It describes how graphs can model real-world data with entities as vertices and relationships as edges. Common machine learning tasks on graphs include identifying influential entities, finding communities, modeling dependencies, and predicting user behavior. The document introduces the concept of graph-parallel programming models that allow algorithms to be expressed by having each vertex perform computations based on its local neighborhood. It presents examples of graph algorithms like PageRank, product recommendations, and identifying leaders that can be implemented in a graph-parallel manner. Finally, it discusses challenges of analyzing large real-world graphs and how systems like GraphLab address these challenges through techniques like vertex-cuts and asynchronous execution.

1. Machine Learning on Graphs
Joseph Gonzalez
Co-Founder, GraphLab Inc.
joseph@graphlab.com
Postdoc, UC Berkeley AMPLab
jegonzal@eecs.berkeley.edu

2. Big
Data
Graphs
More
Signal
More
Noise
2!

3. Social Media
Science
Advertising
Web
Graphs encode relationships between:
People
Products
Ideas
Facts
Interests
Big: billions of vertices and edges & rich metadata
Facebook
(10/2012):
1B
users,
144B
friendships
Twi>er
(2011):
15B
follower
edges
3

4. Graphs are Essential to "
Data Mining and Machine Learning
Identify influential people and information
Find communities
Understand people’s shared interests
Model complex data dependencies

5. Predicting User Behavior
?
?
?
Liberal
?
?
?
Conservative
?
?
?
Post
Post
?
?
Post
Post
Post
?
Post
?
Post
Post
?
?
?
Post
?
Post
Post
Post
?
Conditional Random Field! ?
?
?
?
?
?
Belief Propagation!
Post
?
?
Post
Post
Post
?
?
?
?
5

6. Finding Communities
Count triangles passing through each vertex:
"
2
3
1
4
Measures “cohesiveness” of local community
Fewer Triangles
Weaker Community
More Triangles
Stronger Community

7. Recommending Products
Users
Ratings
Items

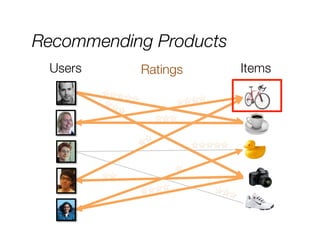
8. Recommending Products
≈
Movies
f(j)
f(i)
Movies
Iterate:
f [i] = arg min
w2Rd
X
j2Nbrs(i)
rij
f(1)
User Factors (U)
Users
Netflix
x
f(2)
T
w f [j]
r13
r14
r24
r25
2
f(3)
f(4)
f(5)
Movie Factors (M)
Users
Low-Rank Matrix Factorization:
+ ||w||2
2
8

9. Identifying Leaders
9

10. Identifying Leaders
R[i] = 0.15 +
X
wji R[j]
j2Nbrs(i)
Rank of
user i
Weighted sum of
neighbors’ ranks
Everyone starts with equal ranks
Update ranks in parallel
Iterate until convergence
10

11. Graph-Parallel Algorithms
Model / Alg.
State
Computation depends
only on the neighbors
11

12. Many More Graph Algorithms
• Collaborative Filtering!
–
–
–
–
• Graph Analytics!
Alternating Least Squares!
Stochastic Gradient Descent!
Tensor Factorization!
SVD!
• Structured Prediction!
– Loopy Belief Propagation!
– Max-Product Linear
Programs!
– Gibbs Sampling!
• Semi-supervised ML!
– Graph SSL !
– CoEM!
–
–
–
–
–
–
PageRank!
Shortest Path!
Triangle-Counting!
Graph Coloring!
K-core Decomposition!
Personalized PageRank!
• Classification!
– Neural Networks!
– Lasso!
…!
12

13. How should we program"
graph-parallel algorithms?
13

14. Structure of Computation
Data-Parallel
Graph-Parallel
Dependency Graph
Table
Row
6. Before
Row
Row
Result
7. After
Row
14
8. After

15. How should we program"
graph-parallel algorithms?
“Think like a Vertex.”
- Pregel [SIGMOD’10]
15

16. The Graph-Parallel Abstraction
A user-defined Vertex-Program runs on each vertex
Graph constrains interaction along edges
Using messages (e.g. Pregel [PODC’09, SIGMOD’10])
Through shared state (e.g., GraphLab [UAI’10, VLDB’12])
Parallelism: run multiple vertex programs simultaneously
16

17. The GraphLab Vertex Program
Vertex Programs directly access adjacent vertices and edges
GraphLab_PageRank(i)
//
Compute
sum
over
neighbors
total
=
0
foreach
(j
in
neighbors(i)):
total
=
total
+
R[j]
*
wji
//
Update
the
PageRank
R[i]
=
0.15
+
total
//
Trigger
neighbors
to
run
again
if
R[i]
not
converged
then
signal
nbrsOf(i)
to
be
recomputed
R[4]
*
w41
4
+
1
+
3
Signaled vertices are recomputed eventually.
2
17

18. Num-­‐Ver1ces
Be>er
Convergence of Dynamic PageRank
100000000
51%
updated
only
once!
1000000
10000
100
1
0
10
20
30
40
Number
of
Updates
50
60
70
18

19. Adaptive Belief Propagation
Challenge = Boundaries
Many
Updates
Splash
Noisy “Sunset” Image
Few
Updates
Cumulative Vertex Updates
Algorithm identifies and focuses
on hidden sequential structure
Graphical Model

20. 6. Before
Graph-­‐parallel
Abstrac(ons
BeDer
for
Machine
Learning
Messaging
i
Synchronous
7. After
8. After
Shared
State
i
Dynamic
Asynchronous
20

21. Natural Graphs
Graphs derived from natural
phenomena
21

22. Properties of Natural Graphs
Regular Mesh
Natural Graph
Power-Law Degree Distribution
22

23. Power-Law Degree Distribution
“Star Like” Motif
President
Obama
Followers
23

24. Challenges
of
High-­‐Degree
VerMces
SequenMally
process
edges
Touches
a
large
fracMon
of
graph
CPU 1
CPU 2
Provably
Difficult
to
ParMMon
24

25. ment. While fast and easy to implement,
placement cuts most of the edges:
Random
ParMMoning
em 5.1. If vertices random
(hashed)
assigne
are randomly
• GraphLab
resorts
to
parMMoning
on
natural
graphs
nes then the expected fraction of edges cut

|Edges Cut|
E
=1
|E|
1
p
10
Machines
!
90%
of
edges
cut
example if just two machines are used, hal
100
Machines
!
99%
of
edges
cut!
Machine
1
Machine
2
es will be cut requiring order |E| /2 commun
25

26. Program
For
This
Run
on
This
Machine 1
Machine 2
• Split
High-­‐Degree
verMces
• New
Abstrac1on
!
Equivalence
on
Split
Ver(ces
26

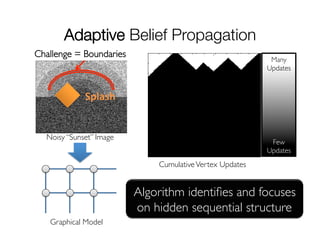
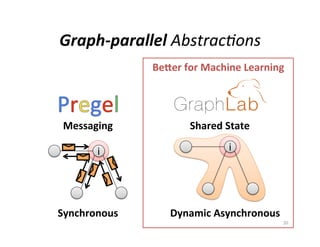
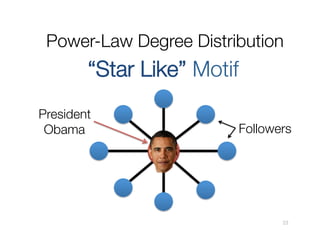
27. A Common Pattern in
Vertex Programs
GraphLab_PageRank(i)
//
Compute
sum
over
neighbors
total
=
0
Gather
Informa1on
foreach(
j
in
neighbors(i)):
About
Neighborhood
total
=
total
+
R[j]
*
wji
//
Update
the
PageRank
Update
Vertex
R[i]
=
total
//
Trigger
neighbors
to
run
again
priority
=
|R[i]
–
oldR[i]|
Signal
Neighbors
&
if
R[i]
not
converged
then
Modify
Edge
Data
signal
neighbors(i)
with
priority
27

28. GAS Decomposition
Machine
1
Machine
2
Master
Gather
Apply
Sca>er
Y’
Y’
Y’
Y’
Σ1
Σ
Σ2
+
+
+
Mirror
Y
Σ3
Σ4
Mirror
Machine
3
Mirror
Machine
4
28

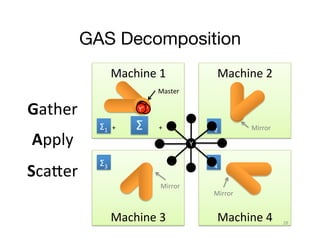
29. Minimizing Communication in
PowerGraph
Y
Communication is linear in "
the number of machines "
each vertex spans
A vertex-cut minimizes "
machines each vertex spans
Percolation theory suggests that power law
graphs have good vertex cuts. [Albert et al. 2000]
29

30. Machine Learning and Data-Mining
Toolkits
Graph
AnalyMcs
Graphical
Models
Computer
Vision
Clustering
Topic
Modeling
CollaboraMve
Filtering
GraphLab2
System
MPI/TCP-­‐IP
PThreads
HDFS
EC2
HPC
Nodes
http://graphlab.org
Apache 2 License

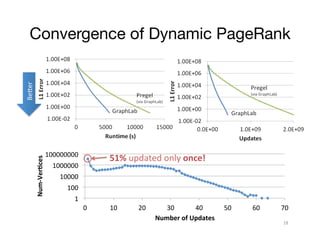
31. PageRank on Twitter Follower Graph
Natural Graph with 40M Users, 1.4 Billion Links
Run1me
Per
Itera1on
0
50
100
150
200
Hadoop
GraphLab
Twister
Piccolo
Order of magnitude
by exploiting
properties of Natural
Graphs
PowerGraph
Hadoop results from [Kang et al. '11]
Twister (in-memory MapReduce) [Ekanayake et al. ‘10]
31

32. GraphLab2 is Scalable
Yahoo Altavista Web Graph (2002):
One of the largest publicly available web graphs
1.4 Billion Webpages, 6.6 Billion Links
7 Seconds per Iter.
1B links Nodes
processed per second
64 HPC
1024 Cores (2048
30 lines of user code
HT)
32

33. Topic Modeling
English language Wikipedia
– 2.6M Documents, 8.3M Words, 500M Tokens
– Computationally intensive algorithm
Million
Tokens
Per
Second
0
Smola
et
al.
PowerGraph
20
40
60
80
100
120
140
160
100 Yahoo! Machines
Specifically engineered for this task
64 cc2.8xlarge EC2 Nodes
200 lines of code & 4 human hours
33

34. Triangle Counting on Twitter
40M Users, 1.4 Billion Links
Counted: 34.8 Billion Triangles
Hadoop
[WWW’11]
1536 Machines
423 Minutes
64 Machines
15 Seconds
1000 x Faster
34
S.
Suri
and
S.
Vassilvitskii,
“CounMng
triangles
and
the
curse
of
the
last
reducer,”
WWW’11

35. 7. After
8. After
By exploiting common patterns in graph data and computation:
New ways to represent
real-world graphs
New ways execute
graph algorithms
Machine 1
Machine 2
Orders of magnitude improvements
over existing systems

36. 7. After
8. After
Possibility
Scalability
Usability

37. Exciting Time to Work in ML
J Unique opportunities to change the world!!
With ML, I will
cure cancer!!!
With ML I will
find true love.
Why won’t
ML read
my mind???
L Building scalable learning system requires experts …

38. But…
Even
basics
of
scalable
ML
can
be
challenging
ML key to any
new service we
want to build
6
months
from
prototype
to
producMon
State-­‐of-­‐art
ML
algorithms
trapped
in
research
papers
Goal of GraphLab 3:
Make large-scale machine learning accessible to all! J

39. Adding a Python Layer
Python
API
Graph
AnalyMcs
Graphical
Models
Computer
Vision
Clustering
Topic
Modeling
CollaboraMve
Filtering
GraphLab2
System
MPI/TCP-­‐IP
PThreads
EC2
HPC
Nodes
HDFS

40. Learning ML with
GraphLab Notebook
https://beta.graphlab.com/examples!

41. Prototype to Production
with Python GraphLab:
Easily install prototype locally
Deploy to the cluster in one step

42. Learn:
GraphLab
Notebook
Prototype:
pip install graphlab
è
local prototyping
Production:
Same code scales
to EC2 cluster

43. GraphLab Toolkits
Highly scalable, state-of-the-art
machine learning straight from python
Graph
Analytics
Graphical
Models
Computer
Vision
Clustering
Topic
Modeling
Collaborative
Filtering

44. Machine Learning on Graphs
partners@graphlab.com
NIPS Workshop on Big Learning: biglearn.org
Lake Tahoe, December 9th
Joseph Gonzalez
Co-Founder, GraphLab Inc.
joseph@graphlab.com