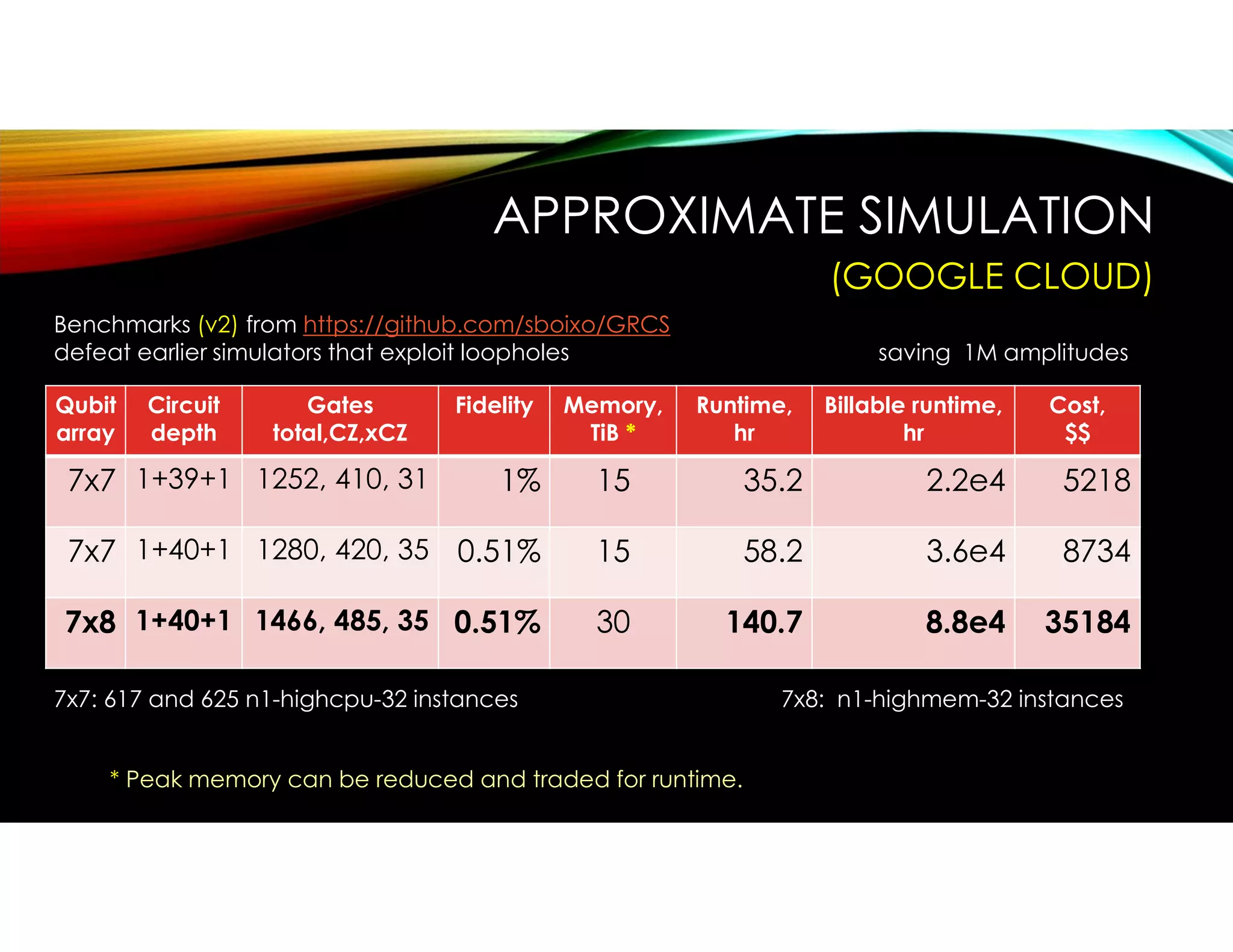
The document discusses the limitations and challenges of quantum computing, emphasizing that while quantum computers may offer computational advantages in specific areas, they do not universally outperform classical computers. It highlights issues such as error accumulation, hardware construction difficulties, and the lack of viable applications, suggesting that practical benefits are more akin to a 'treasure hunt' than a 'gold mine.' The necessity for improved simulation methods and ongoing advancements in classical computing further complicate the prospects of quantum computing achieving a significant competitive edge.

1. QUANTUM COMPUTING:
A TREASURE HUNT
NOT A GOLD MINE
Igor L. Markov
U. Michigan

2. WHY NQI?
Q. Computing
Computational
advantage
•Simulating QM
•Non-quantum
Q. Comms
Secure comms
via QKD
Entanglement
networks
Q. Sensing and
metrology
Atomic clocks
and ultra-
precise sensors

3. ERROR-FREE QUANTUM ALGORITHMS
• No new decision powers (proof by simulation)
• No NP-complete problems solved exactly in poly time
• No asymptotic speed-up for sorting, etc
• Hence, no universal speed-up
• No speedup from single gates expected
• Main promise is in accelerators
• Surprisingly few good applications
• Surprisingly difficult to build hardware

4. NOISE AND ERROR CORRECTION
• Entangled states globalize noise & errors:
local faults have global effects
• No error masking by gates
• Errors accumulate multiplicatively:
• 500 gates with 0.995 fidelity
 0.995500 ~ 0.082 circuit fidelity
• Error correction by duplication and majority not available
• Quantum error correction has much greater overhead

5. BEATING CONVENTIONAL COMPUTERS?

6. BEATING CONVENTIONAL COMPUTERS?
• Strengths of conventional digital computers
• Tiny devices & cheap materials
• Fast interconnect compatible with devices
• Scalable & accurate manufacturing
• Reliable, low-power operation
• Memory hierarchies & cheap ECC
• High-bandwidth I/O
• Verification & test
• Abstraction hierarchy
• Programmability, universality
• Large market & investment; clouds
• Numerous algorithms, some optimal
• Additional efficiencies by orders of magnitude

7. QC: GOLD RUSH OR A TREASURE HUNT?

8. VERIFY CORRECTNESS
DEMONSTRATE AN END-TO-END ADVANTAGE
OVER HIGHLY OPTIMIZED CLASSICAL SYSTEMS

9. DILEMMA FOR NISQ APPS
1. Known computational problems + inputs relevant to applications
• Asymptotically optimal algorithms
• Good heuristics exploit problem structure
• Big data  need big memory and wide I/O
• Ongoing improvements in algorithms and HW
2. Emerging and made-up problems + contrived inputs
• What quantum computers do best, may be useless
• Baseline for conventional computing unknown & likely to improve
• Recent leaps in massively parallel simulation, HW improvements

12. • Input: description of a quantum circuit
• Defines the probability distribution
of measurement outcomes
• Output: samples from the distribution
• Some error allowed (approximation)
• Hardness results for certain circuits
(under mild assumptions)
• Worst-case and average-case results
• Exact sampling on classical computer
• Approximate sampling
• “Imminent availability” on QCs
CIRCUIT SAMPLING PROBLEMS

13. FROM AMPLITUDES TO SAMPLES
• A quantum computer: one amplitude at a time <x | U y>
• How many amplitudes does a simulator need to produce on n qubits?
• One is not enough
• 2n are way too many
• Basic rejection sampling
• Pick M values of y uniformly at random
• r = <x | U y>, then p(y) = r r*
• Discard all y with p(y) > M/2n
• Accept each y with probability p(y) 2n / M
• For n=49 and statistical error 10-4, need M = 41
• Frugal rejection sampling: M’ =10 (arxiv:1807.10749)
• Verification
• Let QC pick y at random
• Compute r=<x | U y>
• Check if p(y) = r r* is heavy
• OR estimate cross-entropy

14. THE NEED FOR FAST CIRCUIT SIMULATION
• To validate QC
• To evaluate architectures and error correction
• To debug and improve QCs
• To set a performance baseline for QC claims
• To price QC

15. STEP ONE
Fast full-memory Schrödinger simulation on a laptop
arxiv:1807.10749

16. NEXT TARGET

18. 5x9 qubits
642 gates, depth 26
Saving 100000 amplitudes
One Xeon server with 96 threads (2.0GHz)
20 min, 17.4 GiB peak RAM, $0.24
STEP TWO

19. NISQ CIRCUITS
Leaky faucets
• Qubits decay
• Quantum gates err
• Errors accumulate without QECC
Unfair competition for common simulators
• Simulated states are stable
• Simulated gates are exact

20. APPROXIMATE SIMULATION OF NISQ CIRCUITS
• Quantum computers lose
information with every gate
a) verify answer & repeat
b) each answer is a vote
• Simulators can stay just above
that data-loss rate…
while using reasonable
memory and runtime

21. Qubit
array
Circuit
depth
Gates
total,CZ,xCZ
Fidelity Memory,
TiB *
Runtime,
hr
Billable runtime,
hr
Cost,
$$
7x7 1+39+1 1252, 410, 31 1% 15 35.2 2.2e4 5218
7x7 1+40+1 1280, 420, 35 0.51% 15 58.2 3.6e4 8734
7x8 1+40+1 1466, 485, 35 0.51% 30 140.7 8.8e4 35184
* Peak memory can be reduced and traded for runtime.
APPROXIMATE SIMULATION
(GOOGLE CLOUD)
Benchmarks (v2) from https://github.com/sboixo/GRCS
defeat earlier simulators that exploit loopholes
7x7: 617 and 625 n1-highcpu-32 instances 7x8: n1-highmem-32 instances
saving 1M amplitudes

22. REACTION FROM GOOGLE
Make the benchmarks harder,
but still feasible on Q computers
• Use q.gates that are
harder to simulate : iSWAP vs CZ
• Apply more gates in parallel
• Reorder gates
to complicate simulation

23. HOW CLOSE IS QUANTUM SUPREMACY?

24. QC AND ML?
• Need to reliably show “strong” quantum supremacy
• Processing large amounts of data on a QC
• “Large” – more than a few hundred floats
• Quantum algorithms with scalable advantage
• Many of the candidates have been “dequantized”
• Simulation of QCs:
• Helps in design
• Indispensable in verification
• Also a performance competitor

25. QC: A TREASURE HUNT NOT A GOLD RUSH