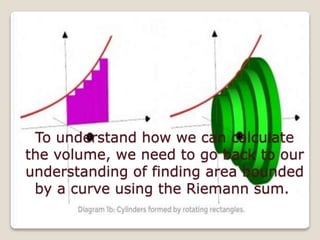
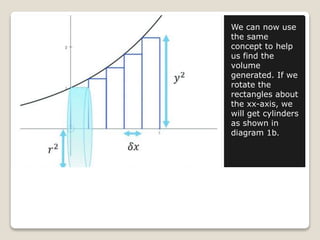
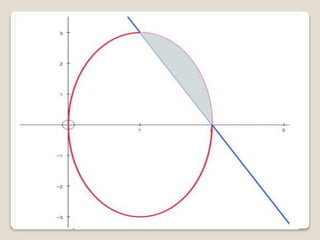
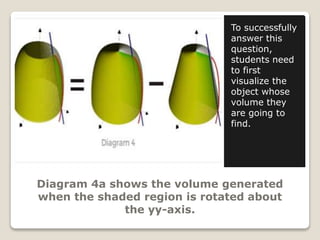
The document discusses how to find the volume generated by rotating an area bounded by a curve, a common challenge in JC math for A-levels. It emphasizes the importance of understanding integration and the visualization of volume, using the concept of Riemann sums to approximate area. Students are advised to approach the problem by visualizing the object and carefully calculating the volume by subtracting the volume generated by a line from that generated by the curve.

1. JC MATH TUITION
A" Levels, applications of integration, H2 math,
integration, Volume

2. HOW TO FIND THE VOLUME
GENERATED BY A CURVE?

3. One of the most problematic topics in A
levels JC math is to find the volume
generated when an area bounded by a
curve is rotated. To do well in this topic,
students not only have to be good at
integration, they must also be able to
imagine and visualize the volume of the
object they are trying to find.

4. To understand how we can calculate
the volume, we need to go back to our
understanding of finding area bounded
by a curve using the Riemann sum.

5.  We can divide the area into
strips of rectangles. It is not
difficult to understand that as
the number of rectangles
increases, the base of each
rectangle, i.e. , δxδx will get
smaller and tend to zero and
the sum of the area of all the
rectangles will be the
approximated area bounded by
the curve. This is called the
Riemann sum, named after the
German mathematician
Bernhard Riemann.

7. We can now use
the same
concept to help
us find the
volume
generated. If we
rotate the
rectangles about
the xx-axis, we
will get cylinders
as shown in
diagram 1b.

11. Diagram 4a shows the volume generated
when the shaded region is rotated about
the yy-axis.
To successfully
answer this
question,
students need
to first
visualize the
object whose
volume they
are going to
find.

12.  Students need to
understand that this
volume cannot be found
in one step. They need
to be able to visualize
that they need to
subtract the volume
generated by the line
(diagram 4c) from the
volume generated by
the curve (diagram 4b)
in order to find the
required volume.

13. CONTACTSUS
 Hope you finds it’s
useful, for more visit
our website.
 Website -
www.jcmath.com.sg
 Tel:
+65 97632567