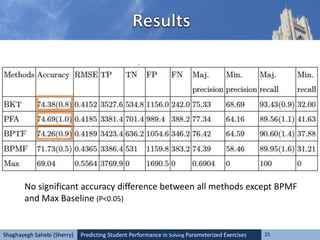
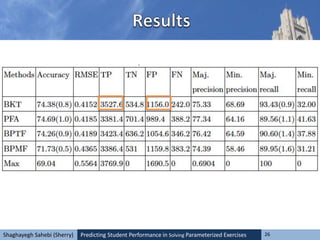
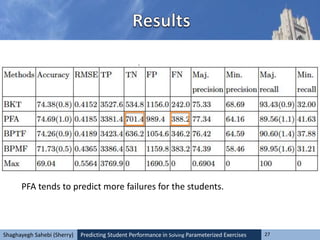
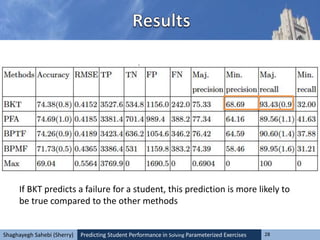
This document explores methods for predicting student performance in solving parameterized exercises, emphasizing the significance of attempt sequences and various modeling approaches like Bayesian methods and collaborative filtering. It suggests that personalized e-learning systems, akin to recommender systems, can enhance the prediction of students' success. Additionally, it discusses the efficacy of different prediction models, noting that time-aware methods outperform time-ignorant ones, and highlights inconsistencies in predicting student success rates across various strategies.

2. Predicting Student Performance in Solving Parameterized Exercises 2Shaghayegh Sahebi (Sherry)
• One question template with multiple
parameter sets
– One template generates many questions
– Each question be repeated multiple times by the
same student
– Makes cheating difficult
– The student can learn by practicing over time

3. Predicting Student Performance in Solving Parameterized Exercises 3Shaghayegh Sahebi (Sherry)

4. Predicting Student Performance in Solving Parameterized Exercises 4Shaghayegh Sahebi (Sherry)
• Unproductive repetitions
– Students who are not good in managing their
learning [Hsiao et. al, 2009]
• How to avoid this?
– Personalized e-learning system
– Predict the success of students’ future attempts
the same way as recommender systems
– Predicting students’ performance (PSP)

5. Predicting Student Performance in Solving Parameterized Exercises 5Shaghayegh Sahebi (Sherry)
• In static questions, the student solves a
problem once
– No attempt sequence on each question
– Time-ignorant methods work well
• Collaborative filtering approaches
• Assumption in parameterized questions: the
student can learn by practicing over time
– Attempt sequence for each student on each
question

6. Predicting Student Performance in Solving Parameterized Exercises 6Shaghayegh Sahebi (Sherry)
• To study the
– recommender systems approaches
– effect of attempt sequence
in PSP for parameterized questions
• Approaches:
– Bayesian Knowledge Tracing (BKT)
– Performance Factor Analysis (PFA)
– Bayesian Probabilistic Matrix Factorization (BPMF)
– Bayesian Probabilistic Tensor Factorization (BPTF)
– Max baseline

7. Predicting Student Performance in Solving Parameterized Exercises 7Shaghayegh Sahebi (Sherry)
• Markov Model with two states
• Models attempt sequence explicitly
K K K
Q Q Q
Initial
knowledge
Learning
P(T)
P(G),
P(S)

8. Predicting Student Performance in Solving Parameterized Exercises 8Shaghayegh Sahebi (Sherry)
• Regression model
• No attempt sequencing but implicitly models
attempt history
m(i, j Î KCs
,k Î items,s,f) = bk
+ (gj
si,j
+ rj
fi,j
)
jÎKCs
å

9. Predicting Student Performance in Solving Parameterized Exercises 9Shaghayegh Sahebi (Sherry)
• From collaborative filtering
• No attempt sequence modeling
• We use Bayesian Probabilistic Matrix
Factorization (BPMF) [Xiong et al., 2010]
• Other models were used for static questions
[Thai-Nghe et al., 2011]
1 0 0 0
1 1 0 1
0 0 1 1
0 0 0 1
Students
Questions/ topics
0.9 0
1.5 0.4
0 1.4
0 0.9
Students
KCs
0.8 0.5 0 0.3
0 0 0.5 0.8
KCs
Questions/ topics

10. Predicting Student Performance in Solving Parameterized Exercises 10Shaghayegh Sahebi (Sherry)
• Adds attempt sequence modeling to BPMF
• We use Bayesian Probabilistic Tensor
Factorization (BPTF)
• Other models used for static questions
Students
Questions/ topics
…

11. Predicting Student Performance in Solving Parameterized Exercises 11Shaghayegh Sahebi (Sherry)
• Predicting success (majority class) for every
attempt

12. Predicting Student Performance in Solving Parameterized Exercises 12Shaghayegh Sahebi (Sherry)
• From QuizJET system
• Java Programming Questions
• Six semesters
• 166 Students
• 103 questions
• 69.04% success records (majority class)

13. Predicting Student Performance in Solving Parameterized Exercises 13Shaghayegh Sahebi (Sherry)
• Time-aware methods:
– BKT: explicitly
– PFA: counting previous success/failure
– BPTF: student’s performance changes smoothly over time
• Time-ignorant methods:
– Matrix factorization (BPMF)
– Max baseline
• Collaborative filtering approaches:
– Tensor factorization (BPTF)
– Matrix factorization (BPMF)
• Knowledge component: question
• 5-Fold user-stratified cross validation
– 80% of users in train data, rest in test data

14. Predicting Student Performance in Solving Parameterized Exercises 14Shaghayegh Sahebi (Sherry)

15. Predicting Student Performance in Solving Parameterized Exercises 15Shaghayegh Sahebi (Sherry)
64
66
68
70
72
74
76
78
Accuracy

16. Predicting Student Performance in Solving Parameterized Exercises 16Shaghayegh Sahebi (Sherry)
900
950
1000
1050
1100
1150
1200
BKT PFA BPTF
False Positive

17. Predicting Student Performance in Solving Parameterized Exercises 17Shaghayegh Sahebi (Sherry)
0
50
100
150
200
250
300
350
400
450
BKT PFA BPTF
False Negative

18. Predicting Student Performance in Solving Parameterized Exercises 18Shaghayegh Sahebi (Sherry)
0
20
40
60
80
100
120
140
BKT PFA BPTF BPMF
Minority Recall
Majority Precision

19. Predicting Student Performance in Solving Parameterized Exercises 19Shaghayegh Sahebi (Sherry)
0
20
40
60
80
100
120
140
160
180
BKT PFA BPTF BPMF
Majority Recall
Minority Precision

20. Predicting Student Performance in Solving Parameterized Exercises 20Shaghayegh Sahebi (Sherry)
• Attempt sequence is important in PSP for
parameterized questions
• Recommender systems approaches are as
good as the pioneers PSP methods
– if they consider attempt sequence
– Do not need to know the exact Knowledge
Components
– Encourages more research on applying more
recommendation techniques in PSP

21. Predicting Student Performance in Solving Parameterized Exercises 21Shaghayegh Sahebi (Sherry)
• Other collaborative filtering approaches
• Ensemble of approaches
• Effect of knowledge structure (our AIEDCS
paper)
• Personalize students’ experience according to
our results

22. Predicting Student Performance in Solving Parameterized Exercises 22Shaghayegh Sahebi (Sherry)
Thank You!

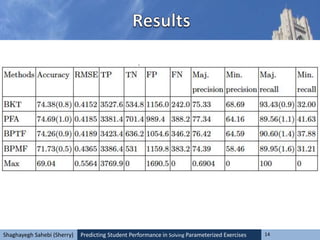
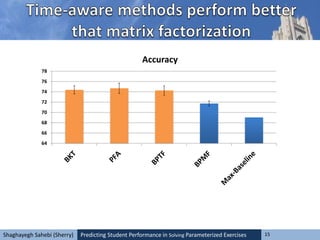
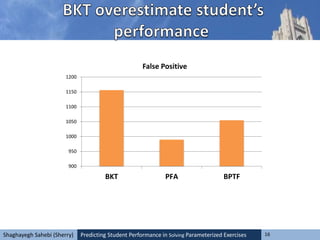
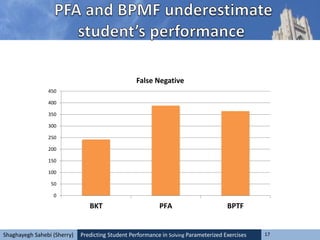
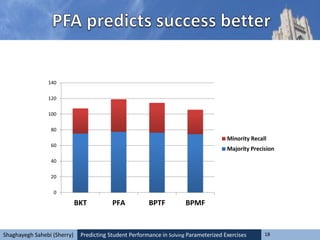
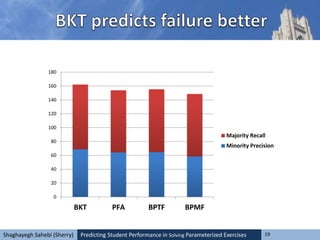
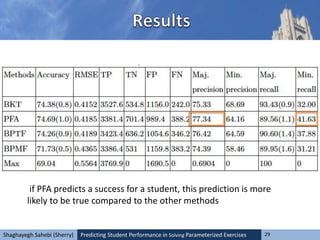
23. Predicting Student Performance in Solving Parameterized Exercises 23Shaghayegh Sahebi (Sherry)
• EM algorithm for BKT and set the initial
parameters as follows: p(L0) = 0:5 , p(G) = 0:2 ,
p(S) = 0:1 , p(T) = 0:3 . For running PFA, we use
• the implementation of logistic regression in
WEKA [3].
• For BPTF and BPMF: Matlab code prepared by
Xiong et. al. We experimented with different
latent space dimensions for BPTF and BPMF (5,
10, 20 and 30) and chose the best one, which has
the latent space dimension of 10

24. Predicting Student Performance in Solving Parameterized Exercises 24Shaghayegh Sahebi (Sherry)
• Predicting the student’s capability to solve a
problem or perform an educational task,
mostly based on her performance in the past
• Predicting success/failure in solving a question
• Questions can be related to topics (Here, each
topic can have multiple questions and each
question is related to one topic)

25. Predicting Student Performance in Solving Parameterized Exercises 25Shaghayegh Sahebi (Sherry)
No significant accuracy difference between all methods except BPMF
and Max Baseline (P<0.05)

26. Predicting Student Performance in Solving Parameterized Exercises 26Shaghayegh Sahebi (Sherry)

27. Predicting Student Performance in Solving Parameterized Exercises 27Shaghayegh Sahebi (Sherry)
PFA tends to predict more failures for the students.

28. Predicting Student Performance in Solving Parameterized Exercises 28Shaghayegh Sahebi (Sherry)
If BKT predicts a failure for a student, this prediction is more likely to
be true compared to the other methods

29. Predicting Student Performance in Solving Parameterized Exercises 29Shaghayegh Sahebi (Sherry)
if PFA predicts a success for a student, this prediction is more
likely to be true compared to the other methods

30. Predicting Student Performance in Solving Parameterized Exercises 30Shaghayegh Sahebi (Sherry)

31. Predicting Student Performance in Solving Parameterized Exercises 31Shaghayegh Sahebi (Sherry)
• Maj. Prec: TP/(TP+FP)
• Min Prec: TN/(TN+FN)
• Maj. Recall: TP/(TP+FN)
• Min Recall: TN/(TN+FP)
• Accuracy: (TP+TN)/all