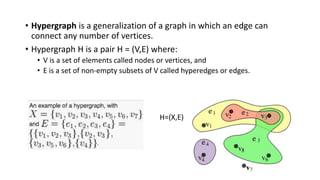
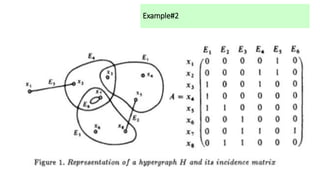
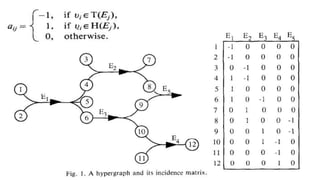
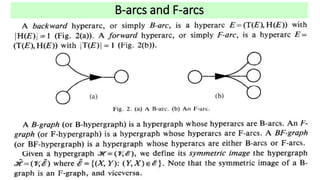
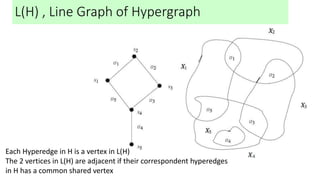
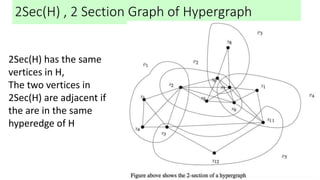
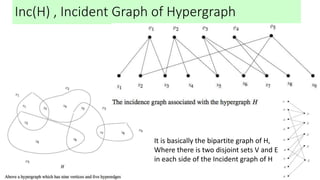
This document introduces hypergraphs, which generalize graphs by allowing edges to connect any number of vertices. It defines hypergraphs and discusses variations such as k-uniform and simple hypergraphs. It also covers representations of undirected and directed hypergraphs, transformations between hypergraph and graph representations, properties like Helly and conformality, and applications in areas like engineering, chemistry, telecommunications, and more.

1. Introduction to
Hypergraphs
Ismael A. Ali
iali1@kent.edu
Semantic Web Meeting | KSU – Dept. of CS | Friday, April 24, 2015

2. Outline
• Hypergraph Definition
• Hypergraph Variations
• Hypergraph Representation
• Hypergraph Types
• Undirected Hypergraphs
• Directed Hypergraph
• Transformations
• Graph representation of Hypergraph
• Hypergraph Properties
• Applications of Hypergraph

3. Hypergraph Definition

4. • Hypergraph is a generalization of a graph in which an edge can
connect any number of vertices.
• Hypergraph H is a pair H = (V,E) where:
• V is a set of elements called nodes or vertices, and
• E is a set of non-empty subsets of V called hyperedges or edges.
H=(X,E)

5. Hypergraph Variations

6. Empty, trivial, uniform, ordered and simple hypergraph
• k-uniform hypergraph: When all hyperedges have the same cardinality; So a 2-uniform
hypergraph is a classic graph, a 3-uniform hypergraph is a collection of unordered triples, and so
on.
• A hypergraph is simple if all edges are distinct
• An r-uniform hypergraph is said to be ordered if the occurrence of nodes in every edge is
numbered from 1 to r.

7. Induced Sub-hypergraph

8. Partial, and regular Hypergraph

9. Examples

10. (Undirected) Hypergraph
Representation

11. (Undirected) Hypergraph Representation

12. Example#2

13. Example#2

14. Hypergraph Types
1. Undirected Hypergraphs
2. Directed Hypergraph

15. 1. Undirected Hypergraphs
…. What mentioned before was undirected
hypergraph

16. 2. Directed Hypergraphs (DH)
DH has 2 models (of visualizing)

17. DH Model#1:
Incidence digraph Dirhypergraph

18. DH Model#2:

20. B-arcs and F-arcs

21. • Transformations
• Graph representation of Hypergraph
1. L(H) , Line Graph of Hypergraph
2. 2Sec(H) , 2 Section Graph of Hypergraph
3. Inc(H) , Incident Graph of Hypergraph

22. L(H) , Line Graph of Hypergraph
Each Hyperedge in H is a vertex in L(H)
The 2 vertices in L(H) are adjacent if their correspondent hyperedges
in H has a common shared vertex

23. 2Sec(H) , 2 Section Graph of Hypergraph
2Sec(H) has the same
vertices in H,
The two vertices in
2Sec(H) are adjacent if
the are in the same
hyperedge of H

24. Inc(H) , Incident Graph of Hypergraph
It is basically the bipartite graph of H,
Where there is two disjoint sets V and E
in each side of the Incident graph of H

25. Hypergraph Properties
1. Helly property
2. Conformality property

26. 1. Helly property

27. 2. Conformality property

28. Applications of Hypergraph

29. List of applications
• Hypergraph Theory and System Modeling for Engineering
• Chemical Hypergraph Theory
• Hypergraph Theory for Telecommunications
• Hypergraph Theory and Parallel Data Structures
• Hypergraphs and Constraint Satisfaction Problems
• Hypergraphs and Database Schemes
• Hypergraphs and Image Processing
• Distributed systems, databases, artificial intelligence
• VLSI design
• Directed hypergraphs can be very useful in many areas of sciences. Indeed
directed hypergraphs are used as models in:
• Formal languages.
• Relational data bases.
• Scheduling.
The application papers are listed
in the last chapter of this book

30. References
Hypergraphs, Volume 45: Combinatorics of
Finite Sets (North-Holland Mathematical Library)
August 18, 1989
Hypergraph Theory: An Introduction (Mathematical
Engineering) April 18, 2013
by Alain Bretto (Author)

31. Thank you.