The document is an overview of a physics textbook, detailing various topics within the field of physics, including the physical world, laws of motion, gravitation, thermodynamics, and the contributions of notable physicists. It explains the relationship between science, physics, engineering, and technology, highlighting their interconnected nature and the role of the scientific method in scientific inquiry. Additionally, it discusses fundamental forces in nature and presents examination questions to reinforce understanding.











![10 PHYSICS
For example : Force = mass × acceleration
= mass ×
1
v–u [LT ]
[M]
t [T]
-
= = [MLT
T–2]
Hence the dimensions of force are 1 in mass 1 in length and (– 2)
in time.
Dimensional Formula :
Unit of a physical quantity expressed in terms of M, L and T is
called dimensional formula. It shows how and which of the
fundamental quantities represent the dimensions.
For example, the dimensional formula of work is [ML2T–2]
Dimensional Equation :
When we equate the dimensional formula with the physical
quantity, we get the dimensional equation.
For example Work=[ML2T–2]
Classification of Physical Quantities (On the basis of dimensions) :
Physical
Quantity
Dimensional
physical quantity
Dimensional
constant
For e.g. c (velocity of light in vaccum)
For e.g. distance, displacement, force, mass, time etc.
For e.g. 0, 1, 2, ....., e, , sin , cos , tan , etc.
q
p q q
For e.g. plane angle, solid angle, strain,
refractive index, dielectric constant, relative density,
specific gravity, poisson's ratio etc.
R(universal gas constant),
stefan's constant), h (Planck's constant),
k (Boltzmann constant), G (universal gravitational constant) etc.
s(
Dimensionless
constant
Dimensional
variable
Dimensionless
variable
Dimensionless
physical quantity
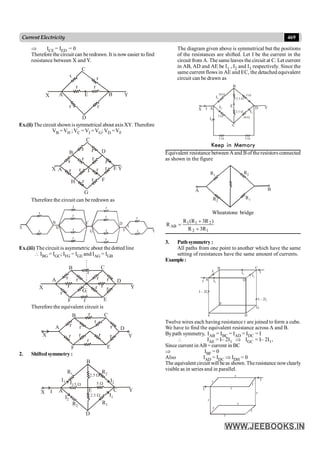
Dimensional Formula of Some Important Physical Quantities :
S.No. Physical quantity Relation with other quantities Dimensional formula
1. Velocity(v)
Length
Time
[M0LT–1]
2. Acceleration (a)
Velocity
Time
[M0LT–2]
3. Momentum (p) Mass × velocity [MLT–1]
4. Force (F) Mass × acceleration [MLT–2]
5. Work Force × displacement [ML2T–2]
6. Power (P) Work
Time
[ML2T–3]
7. Universal gravitational constant
2
1
2
m
m
Fr
G = [M–1L3T–2]
8. Torque F
r ´
=
t [ML2T–2]
9. Surface tension
F
S =
l
[MT–2]
10. Gravitational potential G
W
V
m
= [M0L2T–2]
11. Coefficient of viscosity
dx
dv
A
F
=
h [ML–1T–1]
12. Impulse Force×time(F×t) [MLT–1]](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-14-320.jpg)
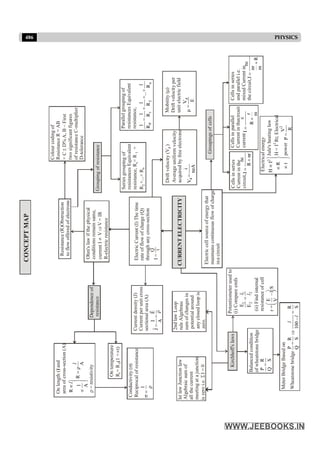
![11
Units and Measurements
13. Strain
Changein length L
Originallength L
D
æ ö
ç ÷
è ø
[M0L0T0]
14. Pressure gradient
Pressure P
Distance
æ ö
ç ÷
è ø
l
[ML–2T–2]
15. Plane angle
Arc s
Radius of circle r
æ ö
ç ÷
è ø
[M0L0T0]
16. Angular velocity
Angle
Time t
q
æ ö
ç ÷
è ø
[M0L0T–1]
17. Radius of gyration
i
Moment of inertia of body I
Total mass of the body m
æ ö
ç ÷
ç ÷
å
è ø
[M0L1T0]
18. Moment of force, moment of couple Force × distance (F × s) [ML2T–2]
19. Angular frequency 2p×frequency(2pn) [M0L0T–1]
20. Pressure
Force
Area
[ML–1T–2]
21. Efficiency
Output work or energy W
Input work or energy Q
æ ö
ç ÷
è ø
[M0L0T0]
22. Angular impulse forque×time (t × t) [ML2T–1]
23. Planck’s constant
Energy E
Frequency
æ ö
ç ÷
n
è ø
[ML2T–1]
24. Heat capacity, Entropy
Heat energy Q
Temperature T
æ ö
ç ÷
è ø
[ML2T–2K–1]
25. Specific heat capacity
Heat energy Q
Mass temperature m T
æ ö
ç ÷
´ ´D
è ø [M0L2T–2K–1]
26. Thermal conductivity, K
Heat energy thickness Q T
KA
Area temperature time t x
´ D
æ ö
= -
ç ÷
´ ´ D
è ø
[MLT–3K–1]
27. Thermal Resistance, R
Length
Thermal conductivity × area
[M–1L–2T3K]
28. Bulk modulus (B) or (compressibility)–1
Volume (changein pressure) P
V
Change in volume V
´ D
æ ö
-
ç ÷
D
è ø
[ML–1T–2]
29. Stefan’s constant (s)
4
4 4
Q AtT
(Energy/area)
Time (temperature) E Q/ A.t T
æ ö
= s
ç ÷
ç ÷
´ = = s
è ø
[ML0T–3K–4]
30. Universal gas constant R
Pressure volume PV
Mole temperature nT
´ æ ö
ç ÷
´ è ø
]
mol
K
T
ML
[ 1
1
2
2 -
-
-
31. Voltage, electric potential (V) or
Work W
Charge q
æ ö
ç ÷
è ø
[ 1
3
2
A
T
ML -
- ]
electromotive force (e)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-15-320.jpg)
![12 PHYSICS
32. Capacitance (C)
Charge q
Potentialdifference V
æ ö
ç ÷
è ø
[ 2
4
2
1
A
T
L
M -
- ]
33. Electricfield ( )
E
r Electric force F
Charge q
æ ö
ç ÷
è ø
[ 1
3
A
MLT -
- ]
34. Magnetic field(B)
r
, magnetic induction,
Force
[F I Bsin ]
Current length
= q
´
l [ML0T–2A–1]
magnetic flux density
35. Magnetic flux (fm) f = BAcosq [ML2T–2A–1]
36. Inductance
m
Magneticflux
Current I
f
æ ö
ç ÷
è ø
[ 2
2
2
A
T
ML -
- ]
coefficient of self inductance (L) or
coefficient of mutual inductance (M)
37. Magnetic field strength or
magnetic moment density(I)
Magneticmoment M
Volume V
æ ö
ç ÷
è ø
[M0L–1T0A]
38. Permittivity constant in free space eo
2 2
2 2
(Charge) q
4π electrostaticforce(distance) 4 F r
æ ö
ç ÷
ç ÷
´ p´ ´
è ø
1 3 4 2
M L T A
- -
é ù
ë û
39. Faraday constant (F), charge Avagadro constant × elementry charge ]
mol
TA
L
M
[ 1
0
0 -
40. Mass defect, (Dm) (Sum of masses of nucleons 0 0
[ML T ]
– mass of nucleus)(MP+MN –Mnucleus)
41. Resonant frequency (fr)
r
1
T ]
T
L
M
[ 1
0
0 -
42. Power of lens
-1 1
(Focal length)
f
æ ö
ç ÷
è ø
0 1 0
M L T
-
é ù
ë û
43. Refractive index
Speedof lightin vacuum
Speedof lightin medium
0 0 0
[M L T ]
44. Wave number
2
Wavelength
p 0 1 0
M L T
-
é ù
ë û
45. Binding energy of nucleus Mass defect × (speed of light in vacuum)2 2 2
ML T-
é ù
ë û
46. Conductance (c)
1
Resistance
1 2 2 3
M L A T
- -
é ù
ë û
47. Fluid flow rate
4
(Pressure) (radius)
8 (Viscosity coefficient) (length)
p ´
æ ö
ç ÷
è ø ´
0 3 –1
M L T
é ù
ë û
48. Inductive reactance (Angular frequency× inductance)
2 3 2
ML T A
- -
é ù
ë û
49. Capacitive reactance (Angular frequency × capacitance)–1 2 3 2
ML T A
- -
é ù
ë û
50. Magnetic dipole moment
Torque
or Current area
Magneticfield
´
0 2 0
M L T A
é ù
ë û](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-16-320.jpg)
![13
Units and Measurements
Short cuts / Time saving techniques
1. To find dimensions of a typical physical quantity which is
involved in a number of formulae, try to use that formula
which is easiest for you. For example if you want to find the
dimensional formula of magnetic induction then you can use
the following formulae
q
=
t
=
m
=
q
p
m
= sin
MB
,
qvB
F
,
nI
B
,
r
sin
Idl
4
dB 0
2
0
Out of these the easiest is probably the third one.
2. Ifyou have tofind the dimensional formula of a combination
of physical quantities, then instead of finding the
dimensional formula ofeach, tryto correlate the combination
ofphysical quantities with a standard formula. For example,
if you have to find the dimension of CV2, then try to use
formula
2
CV
2
1
E = where E is energyofa capacitor.
.
3. =
=
e
m
c
1
0
0
velocityof light in vacuum
• Dimensions ofthe following are same
2
2
2
2
LI
t
R
V
c
q
CV
qV
nRT
PV
Work =
´
=
=
=
=
=
=
[ML2T–2]
• Dimensions ofthe following are same
Force = Impulse / time
= q v B = q E
= Thrust
= weight = energygradient [MLT–2]
• The dimension of RC =
R
L
is same as that of time
• Dimensions ofthe following are same
velocity =
0 0
T 1
f
= = ´l
m m e
[M°LT
T–1]
• Dimensions ofthe following are same
Frequency
R k MB 1
L m I LC
= = = = [M°L°T–1]
• Dimensions ofthe following are same
(E) Modulus of elasticity =Y (Young's modulus)
= B (Bulk modulus)
= h (Modulus of rigidity)
= Stress
= Pressure =
ility
Compressib
1
[ML–1T–2]
• Dimensions ofthe following are same
Acceleration, retardation, centripetal acceleration, centrifugal
acceleration, gravitational intensity/strength. [M°LT–2]
• Dimensions ofthe following are same
Water equivalent, thermal capacity, entropy, Boltzmann's
constant. [ML2T–2K–1]
Keep in Memory
The dimensional formula of
• all trigonometricratio is [M0L0T0]
• x in ex is [M0L0T0]
• ex is [M0L0T0]
• x in log x is [M0L0T0]
• log x is [M0L0T0]
Example1.
Find out the unit and dimensions of permittivity of free
space.
Solution :
According to Coulomb’s law
2 2
2
1 3 4 2
0 2 2 2
A T
[q ]
[M L T A ]
4 [F][r ] [MLT ][L ]
- -
-
é ù
ë û
e = = =
p
Its unit =
2 2
2
coulomb (coulomb) coulomb
joule metre volt metre
newton metre
= =
´ ´
´
CV–1m–1
Example2.
Find out the unit and dimensions of coefficient of self or
mutual inductance of.
Solution :
e = ÷
ø
ö
ç
è
æ
dt
d
L
I
or ÷
ø
ö
ç
è
æ
dt
d
M
I
, where e is induced electromotive
force(e.m.f.)
dt W t
L e
d q
æ ö æ ö
= =
ç ÷ ç ÷
è ø è ø
I I
or [L] = ]
A
T
ML
[
]
A
][
AT
[
]
T
][
T
ML
[ 2
2
2
2
2
-
-
-
=
Its unit is volt × sec/amp or ohm × sec or henry.
Example3.
Find out the unit and dimensions of magnetic field intensity .
Solution :
As B = mH, hence
2
r
sin
d
4
1
B
H
q
p
=
m
=
l
I
;
1
2
[A][L]
H [M L T A]
[L ]
-
= = ° °
Its unit is ampere /metre in SI system. In c.g.s. system, the
unit is oersted.
Example4.
Find out the unit and dimensions of magnetic permeability
of free space or medium.
Solution :
According to Biot-Savart’s law
2
0
r
sin
d
4
B
q
p
m
=
l
I
and F = BI l sinq
or 0
2
d sin
F
B
sin 4 r
m q
= =
q p
l
l
I
I
;](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-17-320.jpg)
![14 PHYSICS
2
0 2 2
Fr
or
m m =
l
I
(dimensionally)
Hence [m] or ]
A
MLT
[
]
L
][
A
[
]
L
][
MLT
[
]
[ 2
2
2
2
2
2
0
-
-
-
=
=
m
Its units are
2
2 2 2 2
N m newton joule/ metre volt coulomb
amp amp metre
amp m amp amp
- ´
= = =
´ ´
-
ohm sec henry tesla metre
metre metre amp.
´ ´
= = =
Example5.
The dimensions of physical quantity X in the equation
Force =
X
Density
is given by
(a) [ML4T–2] (b) [M2L–2T–1]
(c) [M2L–2 T–2] (d) [ML–2T–1]
Solution :
(c) Q Force =
X
denisty
X = Force × density
Hence X has dimensions
[MLT–2] 3
[M]
[L ]
= [M2L–2T–2]
Example6.
If force, acceleration and time are taken as fundamental
quantities, then the dimensions of length will be-
(a) [FT2] (b) [F–1A2T–1]
(c) [FA2T] (d) [AT2]
Solution :
(d) x y z
L F A T
=
0 1 0 2 x 2 y z
M L T [MLT ] [LT ] T
- -
=
= x x y 2x 2y z
M L T
+ - - +
x = 0, x + y= 1, – 2x – 2y+z = 0
x =0, y= 1, z = 2
Hence, 2
L AT
=
DIMENSIONAL ANALYSIS AND ITS APPLICATIONS
Principle of Homogeneity:
Only those physical quantities can be added /subtracted/equated
/compared which have the same dimensions.
Uses of Dimensions :
(1) Conversion of one systemof unit intoanother
Example : Convert a pressure of 106 dyne/cm2 in S.I units.
Sol. We know that 1N = 105 dyne Þ 1 dyne = 10–5 N
Also1m = 100 cm Þ 1cm = 10–2 m
Now, the pressure 106 dyne/cm2 in SI unit is
106 2
5
2
2
–
5
6
m
/
N
10
m
10
m
10
N
10
10
cm
cm
dyne
=
´
´
=
´ -
-
(2) Checking the accuracy of various formulae
Example : Check the correctness of the following
equation dimensionally
dv
F = ηA sinθ
dx
where F=force, h =coefficientofviscosity,
,
A = area,
dv
= velocity
dx
gradient w.r.t distance, q = angle of
contact
Sol. L.H.S = force = [MLT–2]
R.H.S=
1
1 1 1 2 2
dv LT
A (sin ) M L T L MLT
dx L
-
- - -
é ù
h q = ´ =
ë û
The equation is dimensionallycorrect.
CAUTION : Please note that the above equation is not correct
numerically. The conclusion is that an equation, if correct
dimensionally, may or may not be numerically correct. Also
remember that if an equation is dimensionallyincorrect, we can
conclude with surety that the equation is incorrect.
(3) Derivationof formula
Example : The air bubble formed by explosion inside water
performed oscillation with time period T which is directly
proportional to Pa db Ec where P is pressure, d is density and E
is the energy due to explosion. Find the values of a, b and c.
Sol. Let us assume that the required expression for time period is
T = K Pa db Ec
where K is a dimensionless constant.
Writing dimensions on both sides,
c
2
2
b
3
a
2
1
1
0
0
]
T
ML
[
]
ML
[
]
T
ML
[
]
T
L
M
[ -
-
-
-
=
]
T
[
]
T
[
]
L
[
]
M
[ 1
c
2
a
2
c
2
b
3
a
c
b
a
=
= -
-
+
-
-
+
+
Equating the powers,
a + b + c = 0 ....(1)
0
c
2
b
3
a =
+
-
- ....(2)
– 2a – 2c = 1 ....(3)
Solving these equations, we get,
a =
6
5
- , b =
2
1
, c =
3
1
.
Limitationsof DimensionalAnalysis:
(1) Noinformation aboutthedimensionlessconstant isobtained
during dimensional analysis
(2) Formula cannot be found if a physical quantityis dependent
on more than three physical quantities.
(3) Formula containing trigonometrical /exponential function
cannot be found.
(4) Ifan equation is dimensionally correct it mayor may not be
absolutely correct.
Example7.
Find the dimensions of a and b in the Van der waal's
equation
æ ö
ç ÷
è ø
2
a
P+ (V - b) = RT
V
where P is pressure and V is volume of gas.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-18-320.jpg)
![15
Units and Measurements
Solution :
Dimensionally
2
a
P [Byprincipleof homogeneity]
V
=
]
T
[ML
a
V
a
T
ML 2
5
2
2
1 -
-
-
=
Þ
=
Þ
AlsodimensionallyV=b [Byprinciple ofhomogeneity]
b= [L3]
Example8.
The formula
2
2
3mg (1 cos )
v
M (1 sin )
- q
=
+ q
l
is obtained as the
solution of a problem. Use dimensions to find whether
this is a reasonable solution (v is a velocity, m and M are
masses, l is a length and g is gravitational acceleration).
Solution :
Dimensions of L.H.S. = [LT–1]2 = [L2T–2]
Dimensions of R.H.S. =
2
2 2
[M][LT ][L]
[L T ]
[M]
-
-
=
Hence formula is reasonable.
Example9.
In the formula; 2 1
2 1
n n
N D
x x
é ù
-
= - ê ú
-
ë û
,
D = diffusion coefficient, n1 and n2 isnumber of molecules
in unit volume along x1 and x2 which represents distances
where N is number of molecules passing through per unit
area per unit time calculate the dimensions of D.
Solution :
By homogeneity theory of dimension
Dimension of (N)
= Dimension of D ×
2 1
2 1
dimension of (n n )
dimension of (x x )
-
-
2
1
L T
= Dimension of D ×
3
L
L
-
Þ Dimensions of 'D' = 3 2
L
L L T
-
´
=
2
L
T
= [L2T–1]
Example10.
Let us consider an equation 2
1
mv mgh
2
= where m is the
mass of the body, v its velocity, g is the acceleration due to
gravity and h is the height. Check whether this equation is
dimensionally correct.
Solution :
The dimensions of LHS are
[M] [L T–1 ]2 = [M] [ L2 T–2] = [M L2 T–2]
The dimensions of RHS are
[M][L T–2] [L] = [M][L2 T–2] = [M L2 T–2]
The dimensions of LHS and RHS are the same and hence
the equation is dimensionallycorrect.
Example11.
A calorie is a unit of heat or energy and it equals about 4.2
J where 1J = 1 kg m2 s–2. Suppose we employ a system of
units in which the unit of mass equals a kg, the unit of
length equals b m, the unit of time isg s. Show that a calorie
has a magnitude 4.2 a–1 b –2 g2 in terms of the new units.
Solution :
1 cal = 4.2 kg m2 s–2.
SI system New system
n1 = 4.2 n2 = ?
M1 = 1 kg M2 = a kg
L1 =1m L2 = b metre
T1 = 1s T2 = g second
Dimensional formula of energyis [ML2T–2]
Comparing with [MaLbTc], we find that
a = 1, b = 2, c = – 2
Now,
a b c
1 1 1
2 1
2 2 2
M L T
n n
M L T
é ù é ù é ù
= ê ú ê ú ê ú
ë û ë û ë û
=
1 2 2
1kg 1m 1s
4.2
kg m s
-
é ù é ù é ù
ê ú ê ú ê ú
a b g
ë û ë û
ë û
= 4.2 a–1 b –2 g2
SIGNIFICANT FIGURES
The number of digits, which are known reliably in our
measurement, and one digit that is uncertain are termed as
significant figures.
Rules to determine the numbers of significant figures:
1. All non-zerodigits are significant. 235.75has fivesignificant
figures.
2. All zeroes between two non-zero digits are significant.
2016.008 has seven significant figures.
3. All zeroes occurring between the decimal point and the non-
zero digits are not significant. provided there is only a zero
to left of the decimal point. 0.00652 has three significant
figures.
4. All zeroes written to the right of a non-zero digit in a number
written without a decimal point are not significant. This rule
does not work if zero is a result of measurement. 54000 has
two significant figures whereas 54000m has five significant
figures.
5. All zeroes occurring to the right of a non-zero digit in a
number written with a decimal point are significant. 32.2000
has six significant figures.
6. When a number is written in the exponential form, the
exponential term does not contribute towards the significant
figures. 2.465 × 105 has four significant figures.
Keep in Memory
1. The significant figures depend upon the least count of the
instrument.
2. The number of significant figure does not depend on the
units chosen.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-19-320.jpg)



![20 PHYSICS
1. Temperature can be expressed as derived quantityin terms
of
(a) length and mass
(b) mass and time
(c) length, mass and time
(d) None of these
2. What is the unit of “a” in Vander Waal’s gas equation?
(a) Atm litre–2 mol2 (b) Atm litre2 per mol
(c) Atm litre–1 mol2 (d) Atm litre2 mol–2
3. Random error can be eliminated by
(a) careful observation
(b) eliminating the cause
(c) measuring the quantitywith more than one instrument
(d) taking large number of observations and then their
mean.
4. Ifeisthecharge, V thepotentialdifference, T thetemperature,
then the units of
eV
T
are the same as that of
(a) Planck’s constant (b) Stefan’s constant
(c) Boltzmann constant (d) gravitational constant
5. If f = x2, then the relative error in f is
(a)
x
x
D
2
(b)
x
x 2
)
(D
(c)
x
x
D
(d) (Dx)2
6. Two quantities A and B have different dimensions which
mathematical operation given below is physically
meaningful?
(a) A/B (b) A+ B
(c) A – B (d) A= B
7. Which of the following systems of units is not based on
units of mass, length and time alone
(a) SI (b) MKS
(b) CGS (d) FPS
8. Unit of latent heat is
(a) J Kg–1 (b) J mol–1
(c) N Kg–1 (d) N mol–1
9. Dyne-sec is the unit of
(a) momentum (b) force
(c) work (d) angular momentum
10. Illuminance of a surface is measured in
(a) Lumen (b) candela
(c) lux (d) luxm–2
11. SI unit of electric polarisation is
(a) Cm–2 (b) coulomb
(c) ampere (d) volt
12. The SI unit of coefficient of mutual inductance of a coil is
(a) henry (b) volt
(c) farad (c) weber
13. Light year is
(a) light emitted by the sun in one year.
(b) time taken by light to travel from sun to earth.
(c) the distance travelled bylight in free space in one year.
(d) time taken by earth to go once around the sun.
14. The SI unit of pressure is
(a) atmosphere (b) bar
(c) pascal (d) mmofHg
15. Electron volt is a unit of
(a) potential difference (b) charge
(c) energy (d) capacity
16. Dimensions of impulse are
(a) ]
T
ML
[ 1
- (b) ]
MLT
[ 2
(c) ]
MT
[ 2
- (d) ]
T
ML
[ 3
1 -
-
17. The S.I. unit of pole strength is
(a) Am2 (b) Am
(c) A m–1 (d) Am–2
18. Which is dimensionless?
(a) Force/acceleration (b) Velocity/acceleration
(c) Volume/area (d) Energy/work
19. Potential is measured in
(a) joule/coulomb (b) watt/coulomb
(c) newton-second (d) None of these
20. Maxwell is the unit of
(a) magnetic susceptibility
(b) intensity of Magnetisation
(c) magneticFlux
(d) magnetic Permeability
21. The mass of the liquid flowing per second per unit area of
cross-section of the tube is proportional to (pressure
difference across the ends)n and (average velocity of the
liquid)m. Which of the following relations between m and n
is correct?
(a) m= n (b) m = – n
(c) m2 = n (d) m = – n2
22. Which of the following is a derived physical quantity?
(a) Mass (b) Velocity
(c) Length (d) Time
23. N kg–1 is the unit of
(a) velocity (b) force
(c) acceleration (d) None of these
24. Which physical quantities have same dimensions?
(a) Moment of couple and work
(b) Force and power
(c) Latent heat and specific heat
(d) Work and power
25. The expression [ML–1 T–2] does not represent
(a) pressure (b) power
(c) stress (d) Young’s modulus](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-24-320.jpg)
![21
Units and Measurements
1. What are the units of magnetic permeability?
(a) Wb A–1 m–1 (b) Wb–1 Am
(c) Wb A m–1 (d) Wb A–1 m
2. The dimensions of pressure gradient are
(a) [ML–2 T–2] (b) [ML–2 T–1]
(c) [ML–1 T–1] (d) [ML–1 T–2]
3. The dimensions of Rydberg’s constant are
(a) [M0 L–1 T] (b) [MLT–1]
(c) [M0 L–1 T0] (d) [ML0 T2]
4. The dimensions of universal gas constant are
(a) [L2 M1 T–2 K–1] (b) [L1 M2 T–2 K–1]
(c) [L1 M1 T–2 K–1] (d) [L2 M2 T–2 K–1]
5. The dimensions of magnetic moment are
(a) [L2 A1] (b) [L2 A–1]
(c) [L2 / A3] (d) [LA2]
6. The dimensions of Wien’s constant are
(a) [ML0 T K] (b) [M0 LT0 K]
(c) [M0 L0 T K] (d) [MLTK]
7. The unit and dimensions ofimpedance in terms of charge Q
are
(a) mho, [ML2 T–2 Q–2] (b) ohm, [ML2 T–1 Q–2]
(c) ohm, [ML2 T–2 Q–1] (d) ohm, [MLT–1 Q–1]
8. If L denotes the inductance of an inductor through which a
current i is flowing, the dimensions of L i2 are
(a) [ML2 T–2]
(b) [MLT–2]
(c) [M2 L2 T–2]
(d) Not expressiblein M, L, T
9. The dimensional formula ofwave number is
(a) [M0 L0 T–1] (b) [M0 L–1 T0]
(c) [M–1 L–1 T0] (d) [M0 L0 T0]
10. The period of a bodyunder S.H.M. is represented by: T = Pa
Db Sc where P is pressure, D is density and S is surface
tension, then values of a, b and c are
(a) 1
,
2
1
,
2
3
- (b) 3
,
2
,
1 -
-
(c)
2
1
,
2
3
,
2
1
-
- (d) 1, 2 1/3
11. The time of oscillation T of a small drop of liquid depends
on radius r, density r and surface tension S. The relation
between them is given by
(a)
3
r
S
T
r
µ (b)
S
r
T
3
r
µ
(c)
r
µ
3
2
r
S
T (d)
S
r
T
3
r
µ
12. Thepotential energyofaparticlevarieswith distance x from
a fixed origin as
B
x
x
A
V
+
= where A and B are constants.
The dimensions ofAB are
(a) 1 5/2 2
[M L T ]
- (b) 1 2 2
[M L T ]
-
(c) 3/ 2 5/2 2
[M L T ]
- (d) 1 7 /2 2
[M L T ]
-
13. Distance travelled by a particle at any instant ‘t’ can be
represented as S =A(t + B) + Ct2. The dimensions of B are
(a) 0 1 1
[M L T ]
- (b) 0 0 1
[M L T ]
(c) 0 1 2
[M L T ]
- - (d) 0 2 2
[M L T ]
-
14. The deBroglie wavelength associated with a particle of mass
m and energy E is h / 2m E . The dimensional formula of
Planck’s constant h is
(a) ]
T
L
M
[ 2
2
2 - (b) ]
T
L
M
[ 1
2 -
(c) ]
LT
M
[ 2
- (d) ]
T
L
M
[ 2
2 -
15. The velocity of a body which falls under gravity varies as ga
hb, where g is acc. due to gravity and h is the height. The
values of a and b are
(a) a = 1, b = 1/2 (b) a = b = 1
(c) a = 1/2, b= 1 (d) a = 1/2; b= 1/2
16. The velocityvofa particle at time t is given by
b
v a t
t c
= +
+
The dimensions of a, b c are respectively
(a) [LT–2], [L], [T] (b) [L2], [T] and [LT2]
(c) [LT2], [LT] and [L] (d) [L], [LT] and [T2]
17. The dimensions of Hubble’s constant are
(a) ]
T
[ 1
- (b) ]
T
L
M
[ 2
0
0 -
(c) ]
MLT
[ 4 (d) 1
[MT ]
-
18. Error in the measurement of radius ofa sphere is 1%. Then
error in the measurement of volumeis
(a) 1% (b) 5%
(c) 3% (d) 8%
19. Subtract 0.2 J from 7.26 J and express the result with correct
number of significant figures.
(a) 7.1J (b) 7.06J
(c) 7.0J (d) 7 J
20. Multiply107.88 by0.610 and express the result with correct
number of significant figures.
(a) 65.8068 (b) 65.807
(c) 65.81 (d) 65.8](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-25-320.jpg)
![22 PHYSICS
21. When 97.52 is divided by2.54, the correct result is
(a) 38.3937 (b) 38.394
(c) 38.39 (d) 38.4
22. Relative density of a metal may be found with the help of
spring balance. In air the spring balancereads (5.00 ± 0.05)
N and in water it reads (4.00 ± 0.05) N. Relative density
would be
(a) (5.00±0.05)N (b) (5.00±11%)
(c) (5.00±0.10) (d) (5.00± 6%)
23. Area of a square is (100 ± 2) m2. Its side is
(a) (10±1)m (b) (10±0.1)m
(c) m
)
2
10
( ± (d) %
2
10 ±
24. Let Q denote the charge on the plate of a capacitor of
capacitance C. The dimensional formula for
C
Q2
is
(a) ]
T
M
L
[ 2
2 (b) ]
LMT
[ 2
(c) ]
MT
L
[ 2
2 - (d) ]
T
M
L
[ 2
2
2
25. IfL and Rdenote inductance and resistance then dimension
of L/R is
(a) ]
T
L
M
[ 0
0
0 (b) ]
T
L
M
[ 0
0
(c) ]
T
L
M
[ 2
0
2 (d) ]
MLT
[ 2
26. The dimensional formula of current densityis
(a) 0 2 1
[M L T Q]
- -
(b) ]
Q
T
L
M
[ 1
1
2
0 -
(c) ]
Q
MLT
[ 1
-
(d) ]
Q
T
ML
[ 2
1
2 -
-
27. The least count ofa stop watch is 0.2 second. The time of20
oscillations of a pendulum is measured to be 25 second.
The percentage error in the measurement of time will be
(a) 8% (b) 1.8%
(c) 0.8% (d) 0.1%
28. The dimensional formula for relative densityis
(a) [M L–3] (b) [M0 L–3]
(c) [M0 L0 T–1] (d) [M0 L0 T0]
29. The solid angle sustended by the total surface area of a
sphere, at the centre is
(a) 4p (b) 2p
(c) p (d) 3p
30. If C and L denote the capacitance and inductance, the
dimensions of LC are
(a) [M0 L0 T–1] (b) [M0 L–1 T0]
(c) [M–1 L–1 T0] (d) [M0 L0 T2]
31. The dimensions of solar constant is
(a) [M0 L0 T0] (b) [MLT–2]
(c) [ML2 T–2] (d) MT–3
32. The dimensions of
hc
e
1 2
o
Î
are
(a) M–1 L–3 T4 A2 (b) ML3 T–4 A–2
(c) M0 L0 T0 A0 (d) M–1 L–3 T2 A
33. The dimensional formula for entropyis
(a) [MLT–2 K1] (b) [ML2 T–2]
(c) [ML2 T–2 K–1] (d) [ML2 T–2 K]
34. Dimensions of specific heat are
(a) [ML2 T–2 K] (b) [ML2 T–2 K–1]
(c) [ML2 T2 K–1] (d) [L2 T–2 K–1]
35. L, C, Rrepresent physical quantities inductance, capacitance
and resistance respectively. The combinations which have
the dimensions of frequency are
(a) 1/RC (b) R/L
(c) LC
/
1 (d) C/L
36. The physical quantity which has the dimensional formula
[M1T–3] is
(a) surface tension (b) solar constant
(c) density (d) compressibility
37. Which of the following is the most accurate?
(a) 200.0m (b) 20 ×101 m
(c) 2 × 102 m (d) data is inadequate
38. The velocity of water waves (v) may depend on their
wavelength l, the density of water r and the acceleration
due to gravity, g. The method of dimensions gives the
relation between these quantities is
(a) v (b) 2
v g
µ l
(c) 2 2
v g
µ l (d) 2 1 2
v g-
µ l
39. The time dependence of a physical quantity p is given by
p = p0 exp. (– a t2), where a is a constant and t is the time.
The constant a
(a) is dimensionless (b) has dimensions T–2
(c) has dimensions T2 (d) has dimensions of p.
40. In the eqn. 2
a
P (V b) constant,
V
æ ö
+ - =
ç ÷
è ø
the unit of a is
(a) dyne × cm5 (b) dyne × cm4
(c) dyne/cm3 (d) dyne × cm2
41. Dimensions of ‘ohm’ are same as (where h is Planck’s
constant and e is charge)
(a)
e
h
(b)
e
h2
(c) 2
e
h
(d) 2
2
e
h
42. The Richardson equation is given by I = AT2e–B/kT. The
dimensional formula for AB2 is same as that for
(a) I T2 (b) kT
(c) I k2 (d) I k2/T
43. The unit of current in C.G..S. system is
(a) 10A (b) 1/10A
(c) 1/100A (d) 1/1000A](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-26-320.jpg)
![23
Units and Measurements
44. Which of the following do not have the same dimensional
formula as the velocity?
Given that m0 = permeabilityof free space, e0 = permittivity
offree space, n = frequency, l = wavelength, P= pressure, r
= density, w = angular frequency, k = wave number,
(a) 0 o
1 m e (b) nl
(c) P/r (d) wk
45. A cubehas numericallyequal volume and surface area. The
volume of such a cube is
(a) 1000unit (b) 200unit
(c) 216unit (d) 300unit
46. A spherical body ofmass m and radius r is allowed tofall in
a medium of viscosity h. The time in which the velocity of
the body increases from zero to 0.63 times the terminal
velocity(v) is called time constant t. Dimensionallytcan be
represented by
(a)
h
p
6
mr2
(b) ÷
÷
ø
ö
ç
ç
è
æ h
p
2
g
r
m
6
(c)
m
6 r v
ph
(d) None of these
47. A quantity is represented by X = Ma Lb Tc. The % error in
measurement of M, L and T are a%, b% and g%
respectively. The % error in X would be
(a) %
)
c
b
a
( g
+
b
+
a (b) %
)
c
b
a
( g
+
b
-
a
(c) %
100
)
c
b
a
( ´
g
-
b
-
a (d) None of these
48. In a Vernier calliper, N divisions of vernier scale coincide
with (N–1) divisions of main scale (in which one division
represents 1 mm). the least count of the instrument in cm.
should be
(a) N (b) N – 1
(c)
N
10
1
(d)
1
N
1
-
49. What is the fractional error in g calculated from
g
/
2
T l
p
= ? Given fraction errors in T and l are ± x and
± y respectively.
.
(a) x+ y (b) x – y
(c) 2x + y (d) 2x – y
50. Conversion of 1 MW power in a New system of units having
basic units of mass, length and time as 10 kg, 1 dm and 1
minute respectively is
(a) 2.16 × 1010 unit (b) 2 × 104 unit
(c) 2.16 × 1012 unit (d) 1.26 × 1012 unit
51. A resistor of 10 k W having tolerance 10% is connected in
series with another resistor of20 k W having tolerance 20%.
The tolerance of the combination will be
(a) 10% (b) 13%
(c) 30% (d) 20%
52. Using mass (M), length(L), time (T) and electric current (A)
as fundamental quantities the dimensions of permittivity
will be
(a) [MLT–1A–1] (b) [MLT–2A–2]
(c) [M–1L–3T+4A2] (d) [M2L–2T–2A2]
53. Thepercentageerrors in the measurement ofmass and speed
are 2% and 3% respectively. The error, in kinetic energy
obtained by measuring mass and speed, will be
(a) 12% (b) 10%
(c) 8 % (d) 2 %
54. The density of a cube is measured by measuring its mass
and length of its sides. If the maximum error in the
measurement ofmass and length are4% and3% respectively,
themaximum error in themeasurement of densitywill be
(a) 7% (b) 9%
(c) 12% (d) 13%
55. The speed of sound in a gas is given by
RT
v
M
g
=
R = universal gas constant,
T = temperature
M = molar mass of gas
The dimensional formula of g is
(a) ]
T
L
M
[ 0
0
0
(b) ]
LT
M
[ 1
0 -
(c) ]
MLT
[ 2
- (d) ]
T
L
M
[ 1
0
0 -
56. Specific gravity has ............ dimensions in mass, ............
dimensions in length and ............ dimensions in time.
(a) 0,0, 0 (b) 0,1, 0
(c) 1,0, 0 (d) 1,1, 3
57. If I is the moment of inertia and w the angular velocity,
,
what is the dimensional formula ofrotational kinetic energy
2
I
2
1
w ?
(a) ]
T
ML
[ 1
2 -
(b) ]
T
L
M
[ 2
1
2 -
-
(c) ]
T
ML
[ 2
2 - (d) ]
T
L
M
[ 2
1
2 -
-
58. Given that r = m2 sin pt , where t represents time. If the unit
of m is N, then the unit of r is
(a) N (b) 2
N
(c) Ns (d) s
N2
59. The dimensional formula of farad is
(a) ]
TQ
L
M
[ 2
1 -
-
(b) 1 2 2 2
[M L T Q ]
- -
(c) ]
TQ
L
M
[ 2
2
1 -
- (d) ]
Q
T
L
M
[ 2
2
1 -
-
60. If time T, acceleration A and force F are regarded as base
units, then the dimensional formula of work is
(a) [FA] (b) ]
FAT
[
(c) ]
FAT
[ 2 (d) ]
T
FA
[ 2](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-27-320.jpg)
![24 PHYSICS
61. Turpentine oil is flowing through a capillary tube of length
l and radius r. The pressure difference between the two
ends of the tube is p. The viscosity of oil is given by :
2 2
p(r x )
4v
-
h =
l
. Here vis velocityof oil at a distance x from
the axis of the tube. From this relation, the dimensional
formula of h is
(a) ]
T
ML
[ 1
1 -
- (b) ]
MLT
[ 1
-
(c) ]
T
ML
[ 2
2 -
(d) ]
T
L
M
[ 0
0
0
62. The dimensional formula of velocity gradient is
(a) ]
T
L
M
[ 1
0
0 -
(b) ]
MLT
[ 1
(c) 0 1
[ML T ]
- (d) ]
LT
M
[ 2
0 -
63. The thrust developed by a rocket-motor is given by
)
P
P
(
A
mv
F 2
1 -
+
= where m is the mass of the gas ejected
per unit time, v is velocity of the gas, A is area of cross-
section of the nozzle, 1
P and 2
P are the pressures of the
exhaust gas and surrounding atmosphere. The formula is
dimensionally
(a) correct
(b) wrong
(c) sometimes wrong, sometimes correct
(d) Data is not adequate
64. IfE, m, J and G represent energy, mass, angular momentum
and gravitational constant respectively, then the
dimensional formula of 2
5
2
G
m
/
EJ is
(a) angle (b) length
(c) mass (d) time
65. In a vernier callipers, ten smallest divisions of the vernier
scale are equal tonine smallest division on the main scale. If
the smallest division on the main scale is half millimeter,
then the vernier constant is
(a) 0.5mm (b) 0.1mm
(c) 0.05mm (d) 0.005mm
66. Avernier calliper has20 divisions on thevernier scale, which
coincide with 19 on the main scale. The least count of the
instrument is 0.1 mm. The main scale divisions are of
(a) 0.5mm (b) 1mm
(c) 2mm (d)
4
1
mm
67. The pitch of the screw gauge is 0.5 mm. Its circular scale
contains 50 divisions. The least count ofthe screw gauge is
(a) 0.001mm (b) 0.01mm
(c) 0.02mm (d) 0.025mm
68. If x = a – b, then the maximum percentage error in the
measurement ofx will be
(a) %
100
b
b
a
a
´
÷
ø
ö
ç
è
æ D
+
D
(b) %
100
b
b
a
a
´
÷
ø
ö
ç
è
æ D
-
D
(c) %
100
b
a
b
b
a
a
´
÷
ø
ö
ç
è
æ
-
D
+
-
D
(d) %
100
b
a
b
b
a
a
´
÷
ø
ö
ç
è
æ
-
D
-
-
D
69. The heat generated in a circuit is given by 2
I
Q = Rt, where
I is current, R is resistance and t is time. If the percentage
errorsin measuring I,Randt are2%,1%and1%respectively,
then themaximum error in measuring heat will be
(a) 2% (b) 3%
(c) 4% (d) 6%
70. The pressure on a square plate is measured by measuring
the force on the plate and length of the sides of the plate by
using the formula 2
F
P =
l
. If the maximum errors in the
measurement of force and length are 4% and 2%
respectively, then the maximum error in the measurement of
pressure is
(a) 1% (b) 2%
(c) 8% (d) 10%
71. In a simple pendulum experiment for the determination of
acceleration due to gravity, time period is measured with an
accuracy of 0.2% while length was measured with an
accuracy of 0.5%. The percentage accuracy in the value of
g so obtained is
(a) 0.25% (b) 0.7%
(c) 0.9% (d) 1.0%
72. The dimensions of a rectangular block measured with
callipershaving least count of0.01 cm are5 mm × 10mm × 5
mm. The maximum percentageerror in the measurement of
the volume of the block is
(a) 5% (b) 10%
(c) 15% (d) 20%
73. Consider the following pairs of quantities
1. Young's modulus; pressure
2. Torque; energy
3. Linear momentum; work
4. Solar day; light year.
In which cases are the dimensions, within a pair, same?
(a) 1 and 3 (b) 1 and 4
(c) 1 and 2 (d) 2 and 4
74. Which one of the following has the same dimension as that
oftime, ifRisresistance, Linductance and C is capacitance?
(a) RC (b) LC
(c)
R
L (d) All of the above
75. The equation of a wave is given by
x
y asin k
v
æ ö
= w -
ç ÷
è ø
, where w is angular velocity and v is
linear velocity. The dimensions of K will be
(a) [T2] (b) [T–1]
(c) [T] (d) [LT]](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-28-320.jpg)
![25
Units and Measurements
76. In the equation X = 3YZ2, X and Z are dimensions of
capacitance and magnetic induction respectively. In MKSQ
system, the dimensional formula for Y is
(a) [M–3 L–2 T–2 Q–4] (b) [M L–2]
(c) [M–3 L–2 Q4 T8] (d) [M–3 L–2 Q4 T4]
77. A force is given by F = at + bt2, where t is time, the
dimensions of a and b are
(a) [M L T–4] and [M L T–1]
(b) [M L T–1] and [M L T0]
(c) [M L T–3] and [M L T–4]
(d) [M L T–3] and [M L T0]
78. The frequency of vibration of a string is given by f =
L
2
n
T
m
, where T is tension in the string, L is the length, n is
number ofharmonics. The dimensional formula for m is
(a) [M0 L T] (b) [M1 L–1 T–1]
(c) [M1 L–1 T0] (d) [M0 L T–1]
79. The dimensions of voltage in terms of mass (M), length (L)
and time (T) and ampere (A) are
(a) [ML2T–2A–2] (b) [ML2T3A–1]
(c) [ML2T–3A1] (d) [ML2T–3A–1]
80. Suppose the kinetic energy of a body oscillating with
amplitude A and at a distance x is given by
2 2
Bx
K
x A
=
+
The dimensions of B are the same as that of
(a) work/time (b) work × distance
(c) work/distance (d) work× time
81. Thedimensions ofmagneticfield in M, L, T and C (coulomb)
are given as
(a) [MLT–1 C–1] (b) [MT2 C–2]
(c) [MT–1 C–1] (d) [MT–2 C–1]
82. Two full turns of the circular scale of a screw gauge cover a
distance of 1mm on its main scale. The total number of
divisions on the circular scale is 50. Further, it is found that
the screw gauge has a zero error of – 0.03 mm. While
measuring the diameter of a thin wire, a student notes the
main scale reading of 3 mm and the number of circulr scale
divisions in line with the main scale as 35. The diameter of
the wire is
(a) 3.32mm (b) 3.73mm
(c) 3.67mm (d) 3.38mm
83. If the dimensions of a physical quantity are given by
Ma Lb Tc, then the physical quantity will be
(a) velocity if a = 1, b = 0, c = – 1
(b) acceleration if a = 1, b = 1, c = – 2
(c) force if a = 0, b = – 1, c = – 2
(d) pressure if a = 1, b = – 1, c = – 2
84. The density ofa material in CGS system ofunits is 4g/cm3.
In a system ofunits in which unit of length is 10 cm and unit
of mass is 100 g, the value of densityof material will be
(a) 0.4 (b) 40
(c) 400 (d) 0.04
85. In an experiment four quantities a, b, c and d are measured
with percentage error 1%, 2%, 3% and 4% respectively.
Quantity P is calculated as follows
P =
3 2
a b
cd
% error in P is
(a) 10% (b) 7%
(c) 4% (d) 14%
86. What is the fractional error in g calculated from
g
/
2
T l
p
= ? Given fractional errors in T and l are ± x
and ± y respectively.
.
(a) x+ y (b) x – y
(c) 2x + y (d) 2x – y
87. The resistance R ofa wire is given bythe relation R = 2
.
r
r
p
l
Percentage error in the measurement ofr, l and r is1%, 2%
and 3% respectively. Then the percentage error in the
measurement ofR is :
(a) 6 (b) 9
(c) 8 (d) 10
88. What are the dimensions of permeability?
(a) [M1L1T1A–2] (b) [M1L1T–2A–2]
(c) [M2L2T1A0] (d) [M1L2T2A–2]
89. The physical quantity having the dimensions
[M–1L–3T3A2] is
(a) resistance (b) resistivity
(c) electrical conductivity (d) electromotive force
90. The time of reverberation of a room Ais one second. What
will be the time (in seconds) of reverberation of a room,
having all the dimensions double of those of room A?
(a) 2 (b) 4
(c)
1
2
(d) 1
91. Which of the following is the unit of molar gas constant?
(a) JK–1 mol–1 (b) Joule
(c) JK–1 (d) J mol–1
92. Densityof liquid is 16.8 gcm–3. Its valuein the International
System of Units is
(a) 3
16.8 kgm- (b) 3
168 kgm-
(c) 3
1680 kgm- (d) 3
16800 kgm-
93. The dimensional formula of couple is
(a) ]
T
ML
[ 2
2 - (b) ]
MLT
[ 2
(c) 1 3
[ML T ]
- - (d) ]
T
ML
[ 2
2 -
-](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-29-320.jpg)

![27
Units and Measurements
10. The mean length ofan object is 5 cm. Which is the following
measurement is most accurate?
(a) 4.9cm (b) 4.805cm
(c) 5.25cm (d) 5.4cm
11. Young's modulus ofsteel is1.9 × 1011 N/m2.When expressed
in CGS units ofdyne/cm2, it will beequal to(1N = 105 dyne,
1 m2 =104 cm2)
(a) 1.9× 1010 (b) 1.9× 1011
(c) 1.9× 1012 (d) 1.9× 1013
12. If momentum (p), area (A) and time (T) are taken to be
fundamental quantities, then energy has the dimensional
formula
(a) [pA–1T1] (b) [p2AT]
(c) [pA–1/2T] (d) [pA1/2T]
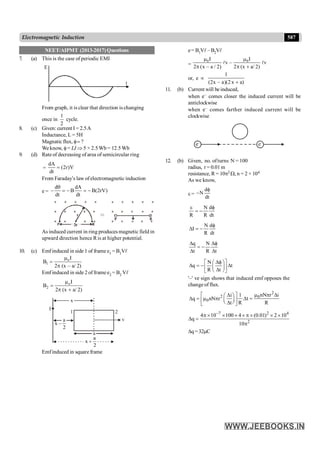
NEET/AIPMT (2013-2017) Questions
13. In an experiment four quantities a, b, c and d are measured
with percentage error 1%, 2%, 3% and 4% respectively.
QuantityP is calculated as follows P =
3 2
a b
cd
% error in P is:
(a) 10% (b) 7% [2013]
(c) 4% (d) 14%
14. The pair of quantities having same dimensions is
(a) Young’s modulus and energy [NEET Kar. 2013]
(b) impulse and surface tension
(c) angular momentum and work
(d) work and torque
15. Ifforce(F),velocity(V)and time(T)aretaken asfundamental
units, then the dimensions of mass are : [2014]
(a) [F V T– 1] (b) [F V T– 2]
(c) [F V– 1 T– 1] (d) [F V– 1 T]
16. If energy (E), velocity (V) and time (T) are chosen as the
fundamental quantities, the dimensional formula of surface
tension will be : [2015]
(a) [EV–1T–2] (b) [EV–2T–2]
(c) [E–2V–1T–3] (d) [EV–2T–1]
17. If dimensions of critical velocity ucof a liquid flowing
through a tube are expressed as x y x
[ r ]
h r , where h, r and
r are the coefficient of viscosity of liquid, density of liquid
and radius of the tube respectively, then the values of x, y
and z are given by : [2015 RS]
(a) –1, –1, 1 (b) –1, –1, –1
(c) 1,1, 1 (d) 1, –1, –1
18. A physical quantityof the dimensions of length that can be
formed out of c, G and
2
0
e
4pe
is [c is velocity of light, G is
universal constant of gravitation and e is charge] [2017]
(a)
1/ 2
2
2
0
e
c G
4
é ù
ê ú
pe
ê ú
ë û
(b)
1/2
2
2
0
1 e
G4
c
é ù
ê ú
pe
ê ú
ë û
(c)
2
0
1 e
G
c 4pe
(d)
1/ 2
2
2
0
1 e
G
4
c
é ù
ê ú
pe
ê ú
ë û](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-31-320.jpg)
![28 PHYSICS
EXERCISE - 1
1. (d) Temperature is one of the basic physical quantities.
2. (b) The vander Waal’s gas equation is
RT
)
b
V
)(
V
a
P
(
2
=
-
+ for one mole.
& =
m
-
÷
÷
ø
ö
ç
ç
è
æ m
+ )
b
V
(
V
a
P
2
mRT for m mole
Dimensionallyin first bracket on L.H.S
m
=
Þ
ú
û
ù
ê
ë
é m
=
2
2
V
]
P
[
]
a
[
V
a
]
P
[
Dimension of
ú
ú
û
ù
ê
ê
ë
é
=
mole
litre
.
atm
]
a
[
2
3. (d)
4. (c) R
T
PV
T
W
T
eV
=
=
=
and
N
R
= Boltzmann constant.
5. (a) 6. (a)
7. (a) SI is based on seven fundamental units.
8. (a)
1
kg
J
kg
J
m
Q
L -
=
=
=
9. (a) As force = change in momentum/time.
force × time= change in momentum
10. (c) Illuminanceis intensityofillumination measured in lux.
11. (a)
2
2
i
Cm
m
C
A
Q
P -
=
=
=
12. (a)
13. (c) 1 light year = speed oflight in vacuum × no. ofseconds
in one year = (3 × 108) × (365 × 24 × 60 × 60) = 9.467 ×
1015 m.
14. (c) 1 pascal = 1 N / m2.
15. (c) Electron volt is a unit of energy &
1eV = 1.6×10–19 joule
16. (a) Impulse = force × time ]
LT
M
[
T
MLT 1
1
2 -
-
=
´
= .
17. (b) Pole strength, .
m
A
m
m
A
2
M
m
2
=
=
=
l
18. (d) Both energy and work have same unit.
energy/work is a pure number.
19. (a) Potential is work done per unit charge.
20. (c) Maxwell is the unit ofmagnetic flux in C.G.S system.
1 Wb(S.I unit) = 108 maxwell
21. (b) Let M = pnvm
m
1
n
2
1
1
2
)
LT
(
)
T
ML
(
T
ML -
-
-
-
-
=
m
n
2
m
n
n
T
L
M -
-
+
-
=
2
m
n
;
1
n -
=
+
-
=
1
1
2
n
2
m -
=
+
-
=
+
-
=
n
m -
=
22. (b)
23. (c) N kg–1 = force/mass = acceleration
24. (a) Moment of couple = force × distance ]
T
L
M
[ 2
2
1 -
=
work = force × distance ]
T
L
M
[ 2
2
1 -
= .
25. (b) ]
T
ML
[
T
T
ML
time
energy
Power 3
2
2
2
-
-
=
=
= .
EXERCISE - 2
1. (a) From Biot Savart’s law
2
0
r
sin
dl
i
4
B
q
p
m
=
2 2 2
1 1
0
4 Br Wb m m
Wb A m
idl sin Am
-
- -
p
m = = =
q
2. (a) Pressure gradient
Pressure difference
distance
= .
[Pressure gradient]
1 2
ML T
L
- -
=
2 2
ML T
- -
é ù
=
ë û
3. (c) From ,
n
1
n
1
R
1
2
2
2
1
÷
÷
ø
ö
ç
ç
è
æ
-
=
l
dimensions of ]
T
L
M
[
L
L
1
R 0
1
0
1 -
-
=
=
=
4. (a)
2 2
PV W ML T
R
T T molK
-
= = =
m m
where m is number of mole of the gas
= [M1L2T–2K–1mol–1]
5. (a) M = current × area =AL2 = [L2 A1]
6. (b) 0 1 0 1
m
b T LK [M L T K ]
= l = =
7. (b)
2 2
1
V W ML T
Impedance
Q Q QT
-
-
= = =
I I
]
Q
T
ML
[ 2
1
2 -
-
= .
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-32-320.jpg)
![29
Units and Measurements
8. (a) Energy stored in an inductor ]
T
ML
[
i
L
2
1 2
2
2 -
=
=
9. (b) Wave number ]
T
L
M
[
L
1
1 0
1
0 -
=
=
l
=
n .
10. (a) T = Pa Db Sc
c
2
b
3
a
2
1
1
0
0
)
MT
(
)
ML
(
)
T
ML
(
T
L
M -
-
-
-
=
c
2
a
2
b
3
a
c
b
a
T
L
M -
-
-
-
+
+
=
Applying principle of homogeneity
a + b + c = 0; – a – 3b = 0; – 2a – 2c = 1
on solving, we get a = – 3/2, b = 1/2, c = 1
11. (b) T
MT
L
ML
S
r
2
3
3
3
=
=
r
-
-
12. (d) x
V
A
;
Vx
x
A
];
L
[
x
B =
=
=
=
2
2
/
5
2
/
1
2
2
T
L
M
L
T
L
M -
-
=
=
]
T
L
M
[
)
L
(
)
T
ML
(
AB 2
2
/
7
1
2
2
/
5 -
-
=
=
13. (b) In S = A(t + B) + Ct2 ; B is added to time t. Therefore,
dimensions of B are those of time.
14. (b) )
T
ML
(
M
L
E
m
2
h 2
2 -
=
l
= ]
T
L
M
[ 1
2 -
=
15. (d) a b
v g h ;
= a
2
b
a
b
a
2
1
0
T
L
L
)
LT
(
]
LT
M
[ -
+
-
-
=
=
2
/
1
a
1
a
2
;
1
b
a =
-
=
-
=
+
2
/
1
b =
16. (a) As c is added to t, c = [T]
1
2
v LT
a [LT ]
t T
-
-
= = = ,
1
b v(t c) LT T [L]
-
= + = ´ =
17. (a) Hubble’s constant,
]
L
[
]
LT
[
ce
tan
dis
velocity
H
1
-
=
=
]
T
[ 1
-
= .
m
/
N
10
70 3
-
´
=
18. (c) ;
r
3
4
V 3
p
=
%
3
%
1
3
100
r
r
3
100
V
V
=
´
=
´
÷
ø
ö
ç
è
æ D
=
´
D
19. (a) Subtraction is correct upto one place of decimal,
corresponding to the least number of decimal places.
7.26–0.2=7.06=7.1J.
20. (d) Number of significant figures in multiplication is three,
corresponding tothe minimum number
107.88× 0.610=65.8068=65.8
21. (d) 4
.
38
393
.
38
54
.
2
52
.
97
=
= (with least number of
significant figures, 3).
22. (d) Relative density =
Weight of body in air
Loss of weight in water
5.00 5.00
5.00 – 4.00 1.00
= =
0.05 0.05
100 100
5.00 1.00
Dr æ ö
´ = + ´
ç ÷
è ø
r
= (0.01 + 0.05) × 100
= 0.06 × 100 = 6%
Relative density = ±
5.00 6%
23. (a) Area = (Length)2
or length 1 2
(Area)
=
1 2
(100 2)
= ±
1 2 1
(100) 2
2
= ± ´
(10 1)m
= ±
24. (c) We know that
C
2
Q2
is energyofcapacitor so it represent
the dimension of energy ]
T
ML
[ 2
2 -
= .
25. (b)
Volt/amp.
sec/amp.
Volt
L/R
´
= = sec. ]
T
L
M
[ 0
0
=
26. (a)
Current Q
Current density
area area t
= =
´
27. (c) 8
.
0
100
25
2
.
0
=
´
28. (d) 29. (a)
30. (d) From
1
2 LC
n =
p
2 0 0 2
2 1 2
1 1
LC T [M L T ]
(2 ) (T )
-
= = = =
p n
31. (d) Solar constant = energy/sec/area
]
MT
[
TL
T
L
M 3
2
2
2
-
-
=
=
32. (c) From
2
2
o r
e
4
1
F
e
p
=
2
o
2
r
F
4
e
p
=
e
(dimensionally)
2 2 2 2
2 1 1
o
e 4 Fr (MLT )L
hc hc ML T [LT ]
-
- -
p
= =
e
]
A
T
L
M
[ 0
0
0
0
= ,
hc
e
o
2
e
is called fine structure constant & has value
137
1
.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-33-320.jpg)
![30 PHYSICS
33. (c)
K
T
ML
T
Q
Entropy
2
2 -
=
= ]
K
T
ML
[ 1
2
2 -
-
=
34. (d)
2 2
2 2 1
Q ML T
s [L T K ]
m MK
-
- -
= = =
q
35. (c)
2 2 2 1 2 4 2
1 1
LC (ML T A ) (M L T A )
- - - -
=
´
=
1
2
1
T
T
-
=
36. (b) Solar constant = energy/area/time
]
T
M
[
T
L
T
L
M 3
1
2
2
2
-
-
=
= .
37. (a)
38. (b) a b c
v k g
= l r
c
2
b
3
a
1
0
)
LT
(
)
ML
(
L
]
LT
M
[ -
-
-
=
c
2
c
b
3
a
b
T
L
M -
+
-
=
1
c
b
3
a
;
0
b =
+
-
=
1
c
2 -
=
- Þ 2
/
1
c =
2
1
a =
1/ 2 0 1/ 2 2
v g or v g
µ l r µ l
39. (b) In p = p0 exp. (– a t2) is dimensionless
]
T
[
T
1
t
1 2
2
2
-
=
=
=
a
40. (b) As P
V
a
2
=
2
a PV
=
3 2 4
2
dyne
(cm ) dyne cm
cm
= = ´
41. (c)
2
3
2
2
1
2
2
A
T
ML
)
AT
(
T
ML
e
h -
-
-
=
= = Resistance (ohm)
42. (c) I = AT2 e–B/kT
Dimensions ofA = I /T2; Dimensions of B = kT
(Q power of exponential is dimensionless)
2 2 2
2
AB (kT) k
T
= =
I
I
43. (a) The C.G.S unit ofcurrent is called biot (Bi) i.e.,
1C (1/10)e.m.u of charge 1
1A Bi
1sec sec 10
= = =
or 1Bi = 10A
44. (d) ]
T
L
[
L
1
T
1
k 1
1 -
-
=
´
=
w
The dimensions of the quantities in a, b, c are of velocity
[LT–1]
45. (c) Volume (L3) = surfacearea (6L2)
L= 6, volume = 63 = 216
46. (d) None of the expressions has the dimensions of time.
47. (a) ;
T
L
M
X c
b
a
=
X a M b L c T
100 100
X M L T
D D D D
æ ö
´ = + + ´
ç ÷
è ø
)%
c
b
a
( g
+
b
+
a
=
48. (c) NVD = (N – 1) MD
MD
N
1
N
VD
1 ÷
ø
ö
ç
è
æ -
=
L.C. = Least count = 1MD – 1VD
MD
N
1
N
1
.
C
.
L ÷
ø
ö
ç
è
æ -
-
=
cm
N
10
1
cm
N
1
.
0
.
D
.
M
N
1
=
=
=
scale
on vernier
parts
of
number
scale
main
on
part
1
of
value
=
whereV.D. = vernier division, M.D. Main scaledivision.
49. (c) From
2
2
T
4
g
;
g
2
T
l
l
p
=
p
=
)
x
2
y
(
T
T
2
g
g
+
=
D
+
D
=
D
l
l
50. (c) We have, n1u1 = n2u2
n2
1
1
2
æ ö
= ç ÷
è ø
u
n
u
2 3
6 1 1 1
2 2 2
10
-
æ ö æ ö æ ö
= ´ ç ÷ ç ÷ ç ÷
è ø è ø è ø
M L T
M L T
3
2
6
1
1 1 1
10
10 60
1 10
kg m s
kg s
m
-
-
æ ö æ ö
æ ö
= ´ ç ÷
ç ÷ ç ÷
è ø
è ø è ø
´
( ) ( )
2 3
6 1
10 10 60
10
æ ö
= ´ ç ÷
è ø
( )3
7
10 60
= ´ = 2.16 × 1012 units.
51. (c) Effective resistance
S
R (10k 10%) (20k 20%)
= W ± + W ±
Tolerance of the combination = 30 30
W ±
( k %)
52. (c) Force, F
2
2
1
0 r
q
q
4
1
pe
=
2
2
1
0
Fr
4
q
.
q
p
=
e
Þ](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-34-320.jpg)
![31
Units and Measurements
So dimension of e0
]
A
T
L
M
[
]
L
][
MLT
[
]
AT
[ 2
4
3
1
2
2
2
-
-
-
=
=
53. (c) Percentage error in mass %
2
100
m
m
=
÷
ø
ö
ç
è
æ
´
D
and
percentage error in speed %
3
100
v
v
=
÷
ø
ö
ç
è
æ
´
D
.
2
1
E mv
2
=
E m V
100 100 2 100
E m V
D D D
´ = ´ + ´
= 2% + 2 × 3% = 8%.
54. (d) Density =
Mass
Volume
3
L
M
=
r ,
L
L
3
M
M D
+
D
=
r
r
D
% error in density= % error in Mass + 3 (% error
in length)
= 4 + 3(3) = 13%
55. (a) Ratio of specific heat,
p
v
C
C
g =
56. (a) Specific gravity is the ratio of density of substance
and densityofwater at 4°C. The ratioof likequantities
is dimensionless.
57. (c) DimensionallyK.E = Work
58. (b) Trigonometric ratio are a number and hence
demensionless
59. (b) 1 2 2 2
Q Q
[C] [M L T Q ]
V W
2
- -
é ù
é ù
= = =
ê ú
ê ú
ë û ê ú
ë û
60. (c) ]
LT
[
]
A
[ 2
-
= or ]
AT
[
]
L
[ 2
=
[Work] = [Force ×Distance] = ]
FAT
[
]
FL
[ 2
=
61. (a) h is the coefficient of viscosity.
.
62. (a) Velocity gradient is velocity per unit distance.
63. (a) Use principle of homogeneity.
64. (a) ]
T
L
M
[
]
T
L
M
][
M
[
]
T
ML
][
T
ML
[ 0
0
0
2
2
3
1
5
2
1
2
2
2
=
-
-
-
-
= angle.
65. (c) 10VD= 9MD, 1VD =
9
MD
10
Vernier constant = 1 MD – 1VD
=
9 1 1 1
1 MD MD
10 10 10 2
æ ö
- = = ´
ç ÷
è ø
=0.05mm
66. (c)
0.1 19
1 MSD
10 20
æ ö
= -
ç ÷
è ø
Þ
1 1
1MSD
100 20
= ´
Þ 1 MSD =
1
10 2
5
´ =
67. (b) Least count
0.5
0.01mm
50
= =
68. (c) Maximum absolute error is b
a D
+
D . Therefore the
percentage error =
absolute error
100
actual value
´
69. (d) 100
t
t
100
R
R
100
I
I
2
100
Q
Q
´
D
+
´
D
+
´
D
=
´
D
2 2% 1% 1%
= ´ + + = 6%.
70. (c)
P F
100 100 2 100
P F
D D D
´ = ´ + ´ =
l
l
4% + 2 × 2%
=8%
71. (c)
2
T
g
,
g
2
T
l
l
µ
p
=
100
g
g
´
D
= 0.5% + 2 × 0.2% = 0.9%
72. (a) % error = 100
5
.
0
01
.
0
100
0
.
1
01
.
0
100
5
.
0
01
.
0
´
+
´
+
´
= 2 + 1 + 2 = 4 + 1 = 5
73. (c)
74. (b) 2 2 2 1 2 4 2
[ LC] ML T A .M L T A T
- - - -
= =
75. (c) The quantity (
v
wx
– wk) has dimension of angle and
hence wk is dimensionless being angle.
76. (d)
1 2 4 2
3 2 4 4
2 2 4 2
[X] M L T A
[Y] M L Q T
[Z ] M T A
- -
- -
- -
= = =
Q
A
T
æ ö
=
ç ÷
è ø
Q
77. (c) [at] = [F] amd [bt2] = [F]
Þ [a] = MLT–3 and [b] = MLT–4
78. (c) Clearly,
2
2 2
n T
m
4f L
= ;
2
2 2
MLT
[m]
T .L
-
-
=
79. (d)
2 2
2 1 3
W ML T
[V] ML A T
Q AT
-
- -
é ù
= = =
ê ú
ë û
80. (b) From 2 2 2
Bx Bx B
K
x
x A x
= = =
+
B = K × x = K.E. × distance = work × distance](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-35-320.jpg)
![32 PHYSICS
81. (c) We know that F = q v B
2
1 1
1
F MLT
B MT C
qv C LT
-
- -
-
= = =
´
82. (d) Least count of screw gauge =
0.5
mm 0.01mm
50
=
Reading = [Main scale reading
+ circular scale reading × L.C] – (zeroerror)
=[3 +35×0.01]–(–0.03)=3.38mm
83. (d) Pressure = [ ]
–2
–1 –2
2
MLT
ML T
L
=
Þ a = 1, b = – 1, c = – 2.
84. (b) In CGS system, 3
g
4
cm
d =
The unit of mass is 100g and unit of length is 10 cm, so
density = 3
100g
4
100
10
cm
10
æ ö
ç ÷
è ø
æ ö
ç ÷
è ø
= 3 3
4
(100g)
100
(10cm)
1
10
æ ö
ç ÷
è ø
æ ö
ç ÷
è ø
3
3
4 100g
(10) ·
100 (10cm)
= ´ = 40 unit
85. (d) P =
3 2
a b
cd
,
P
P
D
× 100% =
a
3
a
D
× 100% +
b
2
b
D
×
100%+
c
c
D
× 100%+
d
d
D
×100%.
= 3 × 1% + 2 × 2% + 3% + 4% = 14%
86. (c) From
2
2
T
4
g
;
g
2
T
l
l
p
=
p
=
)
x
2
y
(
T
T
2
g
g
+
=
D
+
D
=
D
l
l
87. (b) Given = 2
R ,
r
r
=
p
l
then
R
100
R
D
´
=
r
100 100 2 100
r
Dr D D
´ + ´ + ´
r
l
l
= 1% + 2% + 2 × 3% = 9%
88. (b) The magnetic field at a point near a long straight
conductor is given by
B =
0 2
.
4
I
r
m
p
Þ 0
m =
4
2
rB
I
p
[m0] =
[ ][ ]
[ ]
r B
I
=
-2 -1
L.MT A
I
F
B
qv
æ ö
=
ç ÷
è ø
Q
= MLT–2A–2
89. (c) Resistivity,
m
ne2t
r =
3 –3 –2
[ML T A ]
r =
So, electrical conductivity
1
s =
r
–1 –3 3 2
[M L T A ]
s =
90. (a) Reverberation time,
t =
forward backward
d d
V V
æ ö æ ö
+
ç ÷ ç ÷
è ø è ø
when dimensions double then, d¢ = 2d
d d 2d 2d d d
t 2
V V V V V V
¢ ¢ æ ö
¢ = + = + = +
ç ÷
è ø
Þ t¢ = 2t
d d
t
V V
æ ö
+ =
ç ÷
è ø
Q
91. (a)
1
1
mol
K
J
K
mol
J
nT
PV
R -
-
=
=
= .
92. (d) 16.8 gcm–3 =16800Kgm–3.
93. (a) Dimensionallycouple = Torque =Work
94. (a) The mean value ofrefractiveindex,
1.34 1.38 1.32 1.36
1.35
4
+ + +
m = =
and
| (1.35 1.34) | | (1.35 1.38) | | (1.35 1.32) | | (1.35 1.36) |
4
- + - + - + -
Dm =
= 0.02
Thus 100
Dm
´
m
=
0.02
100 1.48
1.35
´ =
95. (b) Least count =
0.1
10
= 0.01 cm
d1
= 0.5 + 8 × 0.01 + 0.03 = 0.61 cm
d2
= 0.5 + 4 × 0.01 + 0.03 = 0.57 cm
d3
= 0.5 + 6 × 0.01 + 0.03 = 0.59 cm
Mean diameter =
0.61 0.57 0.59
3
+ +
= 0.59 cm
96. (d) As,
2
2
g 4
T
= p
l
So,
g T
100 100 2 100
g T
D D D
´ = ´ + ´
l
l
0.1 1
100 2 100
20 90
= ´ + ´ ´ = 2.72 ; 3%
97. (c) 98. (b)
99. (b) 100. (a)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-36-320.jpg)
![33
Units and Measurements
EXERCISE - 3
Exemplar Questions
1. (b) In 0.06900, the twozeroes before six are not siginificant
and two zeroes on right side of9 are significant figures.
Hence, number of significant figures are four (6900).
2. (b) In addition the result will be in least number of places
after decimal andminimum number of significant figure.
The sum of the given numbers can be calculated as
663.821. Thenumber with least decimal places is 227.2
is correct to only one decimal place but in addition of
numbers, the final result should be rounded off to one
decimal place i.e., 664.
3. (c) As we know that in multiplication or division, the final
result should retain as many significant figures as are
there in the original number with the least significant
figures.
Thesignificant figure in given numbers4.237 g and2.5
cm3 are four and two respectivey so, density should
be reported to two significant figures.
3
3
4.237 g
Density 1.6948 1.7 g.cm
2.5 cm
-
= = =
As rounding off the number upto 2 significant
figures, we get density = 1.7.
4. (d) Rounding off2.745 upto 3 significant figures here IVth
digit is 5 and its preceding is even, so no change in 4.
Thus answer would be 2.74. Rounding off 2.735 upto3
significant figures, here IV digit is 5 and its preceding
digit is 3 (odd). So 3 is increased by 1 answer become
would be 2.74.
5. (a) If Dx is error in a physical quantity, then relativeerror is
calculated as
Dx
x
.
Given that,
Length l = (16.2 ± 0.1) cm
Breadth b = (10.1 ± 0.1) cm
Q Dl = 0.1 cm, Db= 0.1 cm
Area (A)= l × b= 16.2×10.1 = 163.62cm2
In significant figure rounding off to three significant
digits, area A = 164 cm2
0.1 0.1
16.2 10.1
D D D
= + = +
A l b
A l b
1.01 1.62 2.63
16.2 10.1 163.62
+
= =
´
So,
2.63 2.63
164
163.62 163.62
D = ´ = ´
A A
= 2.636 cm2
Now rounding off up to one significant figure
DA =3cm2.
So,Area A = A ± DA =(164 ±3) cm2.
6. (c) a. Work = force × distance
= [MLT–2][L] = [ML2T–2]
Torque = F × d = [ML2T–2]
LHS and RHS has same dimensions.
b. Angular momentum (L)
= mvr=[M][LT–1][L]
= [ML2T–1]
Planck's constant h =
n
E
2 2
2 1
1
[ML T ]
[ML T ]
[T ]
-
-
-
= =
1
and
æ ö
= n n =
ç ÷
è ø
E h
T
Q
So, dimensions of h and L are equal.
c. Tension = force = [MLT–2]
Surface tension
2
force [MLT ]
length [L]
-
= =
=[ML0T–2]
d. Impulse= force ×time = [MLT–2][T]
= [MLT–1]
Momentum = mass × velocity
= [M][LT–1] = [MLT–1]
LHS and RHS has same dimensions.
Hence only (c) options of Physical quantities does not
have same dimensions.
7. (a) By applying the Rule of significant figure in
multiplication and addition.
As given that,
A = 2.5ms–1 ± 0.5 ms–1, B = 0.10s ± 0.01 s
x = AB = (2.5)(0.10) = 0.25 m (consider onlysignificant
figure value)
D D D
= +
x A B
x A B
0.5 0.01 0.05 0.025 0.075
2.5 0.10 0.25 0.25
D +
= + = =
x
x
Dx =0.075=0.08m
(rounding off to two significant figures.)
AB =(0.25±0.08)m
8. (d) As given that,
A = 1.0m ±0.2 m, B =2.0m ±0.2m
So, X = (1.0)(2.0)
=
AB = 1.414 m
Rounding off upto two significant digit
X =1.4 m=(r) (Let)
1 1 0.2 0.2
2 2 1.0 2.0
D D D
é ù é ù
= + = +
ê ú ê ú
ë û ë û
x A B
x A B
0.6
2 2.0
=
´
0.6 0.6 1.4
0.212
2 2.0 2 2.0
´
Þ D = = =
´ ´
x
x
Rounding off upto one significant digit
Dx =0.2 m = Dr (Let)
So, correct value of
= + D
AB r r =(1.4 ±0.2)m](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-37-320.jpg)
![34 PHYSICS
9. (a) For the most precise measurement, the unit must be
least and number of digits including zeroes after
decimal must be zero.
Now, take first option,
As here 5.00 mm has the smallest unit and the error in
5.00 mm is least (commonly taken as 0.01 mm if not
specified), hence, 5.00 mm is most precise.
10. (a) Now, checking the errors with each options one by
one,
|Dl1|= |5 –4.9|= 0.1cm
|Dl2|=|5–4.805|= 0.195cm
|Dl3|=|5.25–5|=0.25cm
|Dl4|= |5.4–5|= 0.4cm
Error Dl1 isleast or minimum.
So, 4.9 cm is most precise.
11. (c) It is given that Young's modulus (Y) is,
Y =1.9 ×1011 N/m2
1N = 105 dyne
So, Y = 1.9 × 1011 × 105 dyne/m2
Convert meter tocentimeter
Q 1m=100cm
Y = 1.9 ×1011 × 105 dyne/(100)2 cm2
= 1.9 × 1016 – 4 dyne/cm2
Y = 1.9 × 1012 dyne/cm2
12. (d) Given that fundamental quantities are momentum (p),
area (A) andtime (T).
Let us consider the dimensional formula for
[ ]
a b c
E p A T
µ
]
= a b c
E kp A T
where k is dimensionless constant of proportionality.
Dimensions ofenergy[E] = [ML2T–2] and Dimension
of momentum p= mv = [MLT–1]
Dimension ofArea [A] = [L2]
Dimension ofTime [T] = [T]
Dimension of energy[E] = [K] [p]a[A]b[T]c
Putting all the dimensions, value
ML2T–2 = [MLT–1]a [L2]b [T]c
= MaL2b + aT–a + c
Byprinciple of homogeneity of dimensions,
a = 1, 2b +a = 2 Þ 2b + 1 = 2 Þ
1
2
=
b
2
- + = -
a c
c = –2 + a = –2 + 1 = –1
So, Dimensional formula (ofenergy)
E = [pA1/2T–1]
1/2 1
[ ]
-
=
E pA T
NEET/AIPMT (2013-2017) Questions
13. (d) P =
3 2
a b
cd
,
P
P
D
× 100% =
a
3
a
D
× 100% +
b
2
b
D
×
100%+
c
c
D
× 100% +
d
d
D
×100%.
= 3 × 1% + 2 × 2% + 3% + 4% = 14%
14. (d) Work = Force × displacement
Torque = Force × force arm
= mass × acceleration × length
= [M] × [LT–2] × [L] = [M L2T–2]
15. (d) Force = mass × acceleration
Þ [Mass]
=
force
acceleration
é ù
ê ú
ë û
=
force
velocity / time
é ù
ê ú
ë û
= [F V– 1 T]
16. (b) Let surface tension
s = Ea VbTc
b
–2
2 –2 a C
MLT L
(ML T ) (T)
L T
æ ö
= ç ÷
è ø
Equating the dimension ofLHS and RHS
ML0T–2 = MaL2a + b T–2a – b + c
Þ a = 1, 2a + b = 0, –2a – b + c = –2
Þ a = 1, b = – 2, c = – 2
Hence, the dimensions of surface tension are
[EV–2 T–2]
17. (d) Applying dimensional method :
vc = hxryrz
[M0LT–1]= [ML–1T–1]x [ML–3T0]y [M0LT0]z
Equating powers both sides
x + y= 0; –x = –1 x =1
1 + y = 0 y = –1
–x – 3y + z = 1
–1 – 3(–1) + z = 1
–1 + 3+ z = 1
z = –1
18. (d) Let dimensions of length is related as,
L
z
2
x y
0
e
[c] [G]
4
é ù
= ê ú
pe
ê ú
ë û
2
0
e
4pe
= ML3T–2
L= [LT–1]x [M–1L3T–2]y[ML3T–2]z
[L] = [Lx + 3y + 3z M –y + z T–x – 2y – 2z]
Comparing both sides
–y+ z = 0 Þ y= z ...(i)
x+ 3y+ 3z =1 ...(ii)
–x – 4z = 0 (Q y= z) ...(iii)
From(i),(ii)&(iii)
z = y=
1
,
2
x = –2
Hence, L =
1/2
2
2
0
e
c G
4
-
é ù
×
ê ú
pe
ê ú
ë û](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-38-320.jpg)
![BASIC DEFINITIONS
Mechanics : Branch of physics, which deals with the study of
objects in rest and in motion.
Statics : Studyof objects at rest or in equilibrium.
Kinematics : Studyof motion of objects without considering the
cause of motion.
Dynamics : Study of motion of objects considering the cause of
motion.
Rest : An object is said to be at rest if it does not change its
position with time, with respect to its surrounding (a reference
point which is generallytaken as origin in numerical problems)
Motion : An object is said tobe in motion if it changes its position
with time, with respect to its surroundings.
Rest and motion are relative terms.
Point mass/Point object : An object is said to be a point mass if
during its motion it covers distance much greater than its own
size.
One dimensional motion : An object travels in a straight line. It is
also called rectilinear or linear motion. The position change of
the object with time in one dimension can be described by only
one co-ordinate.
Ex. Astone falling freelyunder gravity.
Two dimensional motion or motion in a plane : For an object
travelling in a plane two coordinates sayX and Y are required to
describe its motion.
Ex. An insect crawling over the floor.
Three dimensional motion : An objecttravels in space.Todescribe
motion of objects in three dimension require all three coordinates
x, yand z.
Ex. Akite flying in the sky.
DISTANCE AND DISPLACEMENT
Distance or Path length : The length of the actual path travelled
by an object during motion in a given interval of time is called
the distance travelled by that object or path length. It is a scalar
quantity.
Displacement : It is the shortest distance between the initial and
final position of an object and is directed from the initial position
to the final position. It is a vector quantity.
Keep in Memory
1. Displacement maybe positive, negative or zero but distance
is always positive.
2. Displacement is not affected by the shift of the coordinate
axes.
3. Displacement of an object is independent of the path
followed by the object but distance depends upon path.
4. Displacement and distance both have same unit as that of
length i.e. metre.
5.
Distance
1
|Displacement|
³
6. For a moving body distance always increases with time
7. For a bodyundergoing one dimensional motion, in the same
direction distance = | displacement |. For all other motion
distance > | displacement |.
SPEED
It is the distance travelled per unit time by an object. It is a scalar
quantity. It cannot be negative.
Uniform speed : An object is said to be moving with a uniform
speed, if it covers equal distances in equal intervals of time,
howsoever small the time intervals maybe.
Non-uniform speed : If an object covers unequal distances in
equal interval of time or equal distances in unequal interval of
time.
Instantaneousspeed : Thespeed ofan object at a particular instant
of time is called the instantaneous speed.
Instantaneous speed, Vinst =
0
lim
D ®
D
=
D
t
s ds
t dt
.
Average speed : It is ratio of the total distance travelled by the
object to the total time taken.
Average speed Vav
x
t
D
=
D
Dimensions : [M0LT-1]; Unit: In SI systems.
VELOCITY
It is the displacement of an object per unit time. It is a vector
quantity. It can be positive negative or zero.
Uniform velocity : An object is said tobemoving with a uniform
velocity, if it covers equal displacements in equal intervals of
time, howsoever small the time intervals maybe.
Non-uniform velocity : If an object covers unequal displacements
in equal interval oftime or equal displacements in unequal interval
of time.
Instantaneous velocity : The velocity of an object at a particular
instant of time is called the instantaneous velocity.
3
Motion in a
Straight Line](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-39-320.jpg)
![36 PHYSICS
Variable or non-uniform acceleration : If the velocity of body
changes in different amounts during same time interval, then the
acceleration of the body is known as variable acceleration.
Acceleration is variable if either its direction or magnitude or
both changes with respect to time. A good example of variable
acceleration is the acceleration in uniform circular motion.
EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
When the motion is uniformlyaccelerated i.e., when acceleration
is constant in magnitude and direction :
(i) v = u + at
(ii) 2
at
2
1
ut
s +
=
(iii) v2 – u2 = 2as
where u = initial velocity; v = final velocity;
a = uniform acceleration and
s = distance travelled in time t,
(iv)
u v
s t
2
+
æ ö
= ç ÷
è ø
(v) Distance travelled in nth second sn = 1)
(2n
2
a
u -
+ ;
sn = distance covered in nth second
Above equations in vector form
,
t
a
2
1
t
u
s
,
t
a
u
v 2
+
=
+
=
)
s
.
a
2
u
.
u
v
.
v
or
(
s
.
a
2
u
v 2
2 r
r
r
r
r
r
r
r
r
r
=
+
=
-
t
)
v
u
(
2
1
s
r
r
r
+
=
When displacement (s) is given as a function of time t [s = f(t)]
then
0
t
s µ Body at rest v = 0 a = 0
1
t
s µ Uniform velocity;
acceleration zero 0
t
v µ a = 0
2
t
s µ Uniform acceleration 1
t
v µ 0
t
a µ
more
or
3
t
s µ Non uniform
acceleration more
or
2
t
v µ more
or
1
t
a µ
We use calculus method (integration and differentiation)
for displacement, velocity, acceleration as a function of time.
We know that ò
=
Þ
= dt
v
s
dt
ds
v ; ò
=
Þ
= dt
a
v
dt
dv
a ;
when a = f(s)
ò
ò =
Þ
= dv
v
ds
a
ds
dv
v
a ,
where s = displacement, v = instantaneous velocity,
a = instantaneous acceleration
Instantaneous velocity,
0
lim
D ®
D
= =
D
r r
r
inst
t
r dr
V
t dt
.
Average Velocity : It is ratio of the total displacement to the total
timetaken.
Average velocity,
D
=
D
r
av
r
v
t
Dimensions : [M0LT–1] ; Unit: In SI system, m/s
Keep in Memory
1. |Average velocity| can be zero but average speed cannot be
zero for a moving object.
2.
|Average velocity|
1
Average speed
£
3. | Instantaneous velocity | = Instantaneous speed.
4. A particle may have constant speed but variable velocity. It
happens when particle travels in curvilinear path.
5. If the body covers first half distance with speed v1 and
next half with speed v2 then
Average speed 1 2
1 2
2
=
+
v v
v
v v
6. If a bodycovers first one-third distance at a speed v1, next
one-third at speed v2 and last one-third at speed v3, then
Average speed 1 2 3
1 2 2 3 1 3
3
=
+ +
v v v
v
v v v v v v
7. If a bodytravels with uniform speed v1 for time t1 and with
uniform speed v2 for time t2, then
Average speed 1 1 2 2
1 2
+
=
+
v t v t
v
t t
ACCELERATION
The rate of change of velocity with respect to time is called
acceleration. It is a vector quantity.
Let velocity changes by v
r
D during some interval of time t
D .
Average acceleration av
a
r
is given by
D
=
D
r
r
av
v
a
t
Instantaneous acceleration a
r
is given by
0
lim
D ®
D
= =
D
r r
r
t
v dv
a
t dt
Its SI unit is meter/sec2 (ms–2).
A body moving with uniform velocity has zero acceleration. It
means that neither its speed nor its direction ofmotion is changing
withtime.
Uniform acceleration : If the velocity of the body changes in
equal amount during same time interval, then the acceleration of
the body is said to be uniform. Acceleration is uniform when
neither its direction nor magnitude changes with respect to time.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-40-320.jpg)

![38 PHYSICS
Solution :
dt
k
x
dx
or
x
k
dt
dx
or
x
k
v =
=
=
Given that when t = 0, x = 0 and when t = t, x = x,
Hence ò
ò =
t
0
x
0
dt
k
x
dx
;
ò
ò =
-
t
0
x
0
½
dt
k
dx
x or [ ]
x
1
1
2 t
0
0
x
k t
1
1
2
- +
é ù
ê ú
=
ê ú
ê ú
- +
ê ú
ë û
or
2
t
k
x
or
t
k
x
2 =
=
Now,
2
t
k
2
t
k
k
v
2
=
ú
û
ù
ê
ë
é
´
=
Thus the velocity varies with time.
Example2.
A particle covers each 1/3 of the total distance with speed
vl, v2 and v3 respectively. Find the average speed of the
particle.
Solution :
Average speed
1 2 3
Total distance travelled s
v
s s s
Total time taken
3v 3v 3v
= =
+ +
Þ
1 2 3
1 2 2 3 3 1
3v v v
v
v v v v v v
=
+ +
Example3.
A cheetah can accelerate from0 to 96 km/h in 2 sec., whereas
a cat requires 6 sec. Compute the average accelerations for
the cheetah and cat.
Solution :
For cheetah | r
a av| = f i
| v v |
t
-
D
r r
=
96km / h 0
2sec
-
=
1000m
96
3600sec
2sec
´
= 15 m/s2
For cat |
r
a av| =
10
96
36
6
´
= 5 m/s2.
Example4.
A particle is moving in east direction with speed 5 m/s.
After 10 sec it starts moving in north direction with same
speed. Find average acceleration.
Solution :
| r
v f| = |
r
v i| = 5 m/s
Acceleration ¹ 0
E
S
N
W
(due to change in direction
of velocityAv. acceleration,
D
r
v =
r
v f –
r
v i =
r
v f + (–
r
v i)
r
a =
f i
v v
t
-
D
r r
=
ˆ ˆ
5j 5i
10
-
Þ
r
a = –
1
2
$
i +
1
2
$
j
|
r
a | =
1
2
1
2
2 2
F
HG I
KJ +
F
HG I
KJ =
1
2
m/s2.
Keep in Memory
1. An object moving under the influence of earth's gravity in
which air resistance and small changes in g are neglected is
called a freely falling body.
2. In the absence of air resistance, the velocity of projection
is equal to the velocity with which the body strikes the
ground.
3. Distance travelled by a freely falling body in 1st second is
always half of the numerical value of g or 4.9 m, irrespective
of height h.
4. For a freely falling body with initial velocityzero
(i) Velocity µ time (v = gt)
(ii) Velocity Distance fallen
µ (v2 = 2gs)
(iii) Distance fallen a (time)2 ÷
ø
ö
ç
è
æ
= 2
gt
2
1
s , where g is the
acceleration due to gravity.
5. If maximum height attained bya body projected vertically
upwards is equal to the magnitude of velocityof projection,
then velocityof projection is 2g ms–1 and time of flight is 4
sec.
6. If maximum height attained bya body projected upward is
equal to magnitude of acceleration due to gravity i.e., 'g',
the time of ascent is 2 sec. and velocity of projection is
2
g .
7. Ratio of maximum heights reached by different bodies
projected with velocities u1, u2, u3 etc. are in the ratio of
3
3
2
2
2
1 u
:
u
:
u etc. and ratio of times of ascent are in ratio of
u1 : u2 : u3 etc.
8. During free fall velocity increases by equal amount every
decend and distance covered during 1st, 2nd, 3rd seconds
offall,are4.9m,14.7m,24.5m.
t = 3
4.9 m
14.7 m
24.5 m
t = 2
t = 1
t = 0
u = 0
9.8 m/s
19.6 m/s
29.4 m/s
9. If a body is projected horizontally from top of a tower, the
time taken by it to reach the ground does not depend on
the velocity of projection, but depends on the height of
tower and is equal to t =
g
h
2
.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-42-320.jpg)


![41
Motionina Straight Line
Example12.
The height of a tower is h metre. A body is thrown from the
top of tower vertically upward with some speed, it takes
t1, second to reach the ground. Another body thrown from
the top of tower with same speed downwards and takes t2
seconds to reach the ground. If third body, released from
same place takes ‘t’ second to reach the ground, then
(a) 1 2
t +t
t =
2
(b)
1
2
t
t =
t
(c)
1 2
2 1 1
= +
t t t
(d) 1 2
t = (t t )
Solution : (d)
Let u be the initial velocity of the body. Then at time t1
2
1
1 t
g
2
1
t
u
h +
-
= ...(1)
and at time t2, h =
2
2
2 t
g
2
1
t
u + ...(2)
From eqs. (1) and (2), we get
2
2
2
2
1
1 t
g
2
1
t
u
t
g
2
1
t
u +
=
+
-
or )
t
t
(
u
)
t
t
(
g
2
1
2
1
2
2
2
1 +
=
-
or )
t
t
(
u
)
t
t
(
)
t
t
(
g
2
1
2
1
2
1
2
1 +
=
-
+
or )
t
t
(
g
2
1
u 2
1 -
= ...(3)
Substituting the value of u in eqn. (2) we get
2
2
2
2
1 t
g
2
1
t
)
t
t
(
g
2
1
h +
-
= or 2
1 t
t
g
2
1
h = ...(4)
For third body,
2
t
g
2
1
h = ...(5)
From eqs. (4) and (5) we get, 1 2
t t t
=
Example13.
A bullet moving with a speed 10 m/s hits the wooden plank
and is stopped when it penetrates the plank 20 cm deep.
Calculate retardation of the bullet.
Solution :
v0 = 10 m/s, v = 0 and s = 20 cm. =
2
0.02m
100
=
Using v2 – v0
2 = 2ax
2 100
0 (10) 2a (0.02) a
2 0.02
-
- = Þ =
´
or a = – 2500 m/s2
Retardation = 2500 m/s2
Example14.
A body covers a distance of 20m in the 7th second and 24m
in the 9th second. How much distance shall it cover in
15th sec?
Solution :
From formula, th
n
S u a(2n –1)
2
1
= +
7
a
S th u (2 7 1)
2
= + ´ - but 7
S th 20m
=
a 13a
20 u 13 20 u
2 2
= + ´ Þ = + ...(1)
also 9
s th 24m
=
17a
24 u
2
= + ...(2)
From eqn. (1)
13a
u 20
2
= - ...(3)
Substitute this value of in eqn. (2)
13a 17a
24 20
2 2
= - +
17a 13a
24 20
2 2
- = -
4a
4
2
= Þ 4 = 2a Þ
2
4
a 2 m /s
2
= =
Substituting this value of a in eqn. (3)
13a
u 20
2
= -
Þ
13 2
u 20 u 20 13
2
´
= - Þ = -
u = 7 m/s
Now, s15th =
a
u (2 15 1)
2
+ ´ -
=
2
7 (29) 7 29 36m
2
+ = + =
Example15.
A train starts from rest and for the first kilometer moves
with constant acceleration, for the next 3 kilometers it has
constant velocity and for another 2 kilometers it moves
with constant retardation to come to rest after 10 min.
Find the maximum velocity and the three time intervals in
the three types of motion.
Solution :
Let the three time intervals be t1 min, t2 min, and t3 min.
respectively.
Let the maximum velocityattained be vm/min.
A B C D
1000m 3000m 2000m
t1 v–t2 t3
For Ato B 1
0 v
1000 t
2
+
æ ö
= ç ÷
è ø Þ 1
vt
2000 = ...........(1)
For B to C 2
vt
3000 = ...........(2)
[Using in both equations disp. = mean vel. × time]
and for C to D 3
v 0
2000 t
2
+
æ ö
= ç ÷
è ø Þ 3
vt
4000 = ...... (3)
Adding eqs. (1), (2) and (3), we get
)
t
t
t
(
v
9000 3
2
1 +
+
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-45-320.jpg)
![42 PHYSICS
3
9000 900 10
v 900 m / min. km 54 km / hr.
10 1/ 60 hr.
-
´
= = = =
Now, from eqs. (1), (2) and (3) we get
1
2000 20 2
t 2 min.
900 9 9
= = = ,
2
3000 10 1
t 3 min.
900 9 3
= = =
and 3
4000 40 4
t 4 min.
900 9 9
= = =
Example16.
A falling stone takes 0.2 seconds to fall past a window
which is 1m high. From howfar above the top of the window
was the stone dropped ?
Solution :
2
1
h gt
2
= ;
2
1
h 1 g(t 0.2)
2
+ = +
2 2 2
1 1 1 1
gt 1 gt g(0.2) g 2 0.2t
2 2 2 2
+ = + + ´ ´
u=0
1m
h
1
1 0.2gt
5
= + ;
4 2
2t t
5 5
= Þ =
1 4 4
h g m
2 25 5
= =
Example17.
From the top of a multi-storeyed building 40m tall, a boy
projects a stone vertically upwards with an initial velocity
of 10 ms–1 such that it eventually falls to the ground. (i)
After how long will the stone strike the ground ? (ii) After
how long will it pass through the point from where it was
projected ? (iii) What will be its velocity when it strikes the
ground ? Take g = 10 ms–2.
Solution :
Using, 2
1
S ut at
2
r r
r
= +
(i) 2
1
40 10t gt
2
- = - or 2
40 10t 5t
- = -
[Q taking g = 10m/s2]
or 2
5t 10t 40 0
- - =
h
v
u
u=10m/s
40m
or
2
10 10 4 5( 40) 10 100 800
t
2 5 10
+ - ´ - + +
= =
´
10 30
4 sec.
10
+
= =
(ii) It will pass from where it was projected after
2 10
t 2 sec.
g
´
= =
(iii) Velocity with which stone strikes the ground
V =10 + g× 2 =30m/s
VARIOUS GRAPHS RELATED TO MOTION
(a) Displacement-time graph - In this graph time is plotted on
x-axis and displacement on y-axis.
(i) For a stationary body (v = 0) the time-displacement
graph is a straight line parallel to time axis.
Displ
Velocity = 0
Time
Body is at rest
(ii) When the velocity of a body is constant then time-
displacement graph will be an oblique straight line.
Greater the slope ÷
ø
ö
ç
è
æ
q
= tan
dt
dx
of the straight line,
higher will be the velocity.
(iii) If the velocity of a body is not constant then the time-
displacement curve is a zig-zag curve.
(iv) For an accelerated motion the slope of time-
displacement curve increases with time while for
decelerated motion it decreases with time.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-46-320.jpg)









![55
Motionina Straight Line
Exemplar Questions
1. Among the four graph shown in the figure there is onlyone
graph for which average velocityover the time interval (O,
T) can vanish for a suitably chosen T. Which one is it?
(a) t
x
(b)
t
x
(c)
x
t
(d)
t
x
2. A lift is coming from 8th floor and isjust about to reach 4th
floor. Taking ground floor as origin and positive direction
upwards for all quantities, which one of the following is
correct?
(a) x < 0, v < 0, a > 0 (b) x > 0, v < 0, a < 0
(c) x > 0, v < 0, a > 0 (d) x > 0, v > 0, a < 0
3. In one dimensional motion, instantaneous speed v satisfies
0
0 v v .
£ <
(a) The displacement in time T must always take non-
negative values
(b) The displacement x in time T satisfies 0 0
– < <
v T x v T
(c) The acceleration is always a non-negative number
(d) The motion has no turning points
4. A vehicle travels half the distance l with speed v1 and the
other half with speed v2, then its average speed is
(a) 1 2
2
+
v v
(b)
1 2
1 2
2 +
+
v v
v v
(c)
1 2
1 2
2
+
v v
v v
(d)
1 2
1 2
( )
+
L v v
v v
5. The displacement of a particle is given byx = (t – 2)2 where
x is in metre and t in second. The distance covered by the
particle in first 4 seconds is
(a) 4m (b) 8m
(c) 12m (d) 16m
6. At a metro station, a girl walks up a stationary escalator in
time t1. If she remains stationary on the escalator, then the
escalator take her up in time t2. The time taken by her to
walk up on the moving escalator will be
(a) 1 2
2
+
t t
(b)
1 2
2 1
-
t t
t t
(c)
1 2
2 1
+
t t
t t
(d) t1 – t2
NEET/AIPMT (2013-2017) Questions
7. Astone falls freely under gravity. It covers distances h1, h2
and h3 in the first 5 seconds, the next 5 seconds and the
next 5 seconds respectively. The relation between h1, h2
and h3 is [2013]
(a) h1 = 2
h
3
= 3
h
5
(b) h2 = 3h1 and h3 = 3h2
(c) h1 = h2 = h3 (d) h1 = 2h2 = 3h3
8. The displacement ‘x’ (in meter) ofa particle of mass ‘m’ (in
kg) moving in one dimension under the action of a force, is
related to time ‘t’ (in sec) by t = 3
x + . The displacement
of the particle when its velocityis zero, will be
[NEET Kar. 2013]
(a) 2m (b) 4m
(c) zero (d) 6m
9. A particle of unit mass undergoes one-dimensional motion
such that its velocity varies according to v(x) = bx–2n
where b and n are constants and x is the position of the
particle. The acceleration ofthe particle as d function of x, is
given by: [2015]
(a) –2nb2x–4n–1 (b) –2b2x–2n+1
(c) –2nb2e–4n+1 (d) –2nb2x–2n–1
10. Ifthe velocityof a particle is v=At + Bt2, whereA and B are
constants, then the distance travelled by it between 1s and
2s is : [2016]
(a)
3
A 4B
2
+ (b) 3A+7B
(c)
3 7
A B
2 3
+ (d)
A B
2 3
+
11. Preeti reached the metrostation and found that the escalator
was not working. She walked up the stationaryescalator in
time t1. On other days, if she remains stationary on the
moving escalator, then the escalator takes her up in time t2.
The time taken by her to walk up on the moving escalator
will be: [2017]
(a) 1 2
2 1
t t
t t
-
(b)
1 2
2 1
t t
t t
+
(c) t1 – t2 (d) 1 2
t t
2
+](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-59-320.jpg)
![56 PHYSICS
EXERCISE - 1
1. (b) 2. (b) 3. (c) 4. (c)
5. (d) 6. (b) 7. (c)
8. (b) 2
)
7
t
(
x
or
)
7
t
(
x +
=
+
=
time
velocity
),
7
t
(
2
dt
dx
µ
+
=
9. (b) a = f t, t
f
dt
dv
a =
= at t = 0, velocity = u
v t
u 0
dv f t dt
=
ò ò , v – u =
2
t
f
2
Þ v = u+
2
t
f
2
NOTE : Do not use v = u + at directly because the
acceleration is not constant.
10. (c) 1 2
dx
v a 2a t
dt
= = + 2
dv
a 2a
dt
= =
11. (d) A B
v tan30º and v tan 60º
= =
A
B
v tan30º 1/ 3 1
v tan 60º 3
3
= = =
12. (a) Let for the first halftime t, the person travels a distance
s1. Hence 1
1 1 1
s
v or s v t
t
= =
For second half time, 2
2 2 2
s
v or s v t
t
= =
Now,
1 2
s s
Total displacement
v
Total time 2t
+
= =
1 2 1 2
v t v t v v
2t 2
+ +
= =
13. (b) When a particle cover half of circle of radius r, then
displacement isAB = 2r
& distance = half ofcircumference of circle = pr
A
B
r
r
pr
14. (d) 2
2
gn
2
1
)
1
n
(
g
2
1
y -
+
=
)
1
n
2
(
2
g
]
n
)
1
n
[(
2
g 2
2
+
=
-
+
= ......(i)
Also, )
1
n
2
(
2
g
h -
= ......(ii)
From (i)and(ii)
y = h + g
15. (a) Differentiate two times and put x = 0.
16. (d) The difference in velocities is increasing with time as
both of them have more constant but different
acceleration.
17. (b) Time taken by the stone to reach the water level
g
h
2
t1 =
Time taken bysound to come to the mouth of the well,
v
h
t2 =
Total time
v
h
g
h
2
t
t 2
1 +
=
+
18. (d) Let the total distance be d. Then for first half distance,
time =
0
v
2
d
, next distance. = v1t and last halfdistance
= v2t
1 2
d
v t v t
2
+ = ;
1 2
d
t
2(v v )
=
+
Now average speed
)
v
v
(
2
d
)
v
v
(
2
d
v
2
d
d
t
2
1
2
1
0 +
+
+
+
=
0 1 2
1 2 0
2v (v v )
(v v ) 2v
+
=
+ +
19. (c) a = bt or bt
dt
dv
= . Integrating, we get
c
2
bt
v
2
+
= , where c is a constant of integration.
At t = 0, v = v0. Thus v0 = c.
Now, o
2
v
2
bt
dt
ds
v +
=
= dt
v
2
bt
ds o
2
÷
÷
ø
ö
ç
ç
è
æ
+
=
Integrating we get, t
v
6
bt
s o
3
+
=
20. (a) 3
kv
dt
dv
-
= or dt
k
v
dv
3
-
=
Integrating we get, c
kt
v
2
1
2
+
-
=
- ...(1)
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-60-320.jpg)
![57
Motionina Straight Line
At t = 0, v = v0 2
o
1
c
2v
- =
Putting in (1)
2 2 2 2
0 0
1 1 1 1
kt or kt
2v 2v 2v 2v
- = - - - = -
or
2
2
0 v
2
1
kt
v
2
1
=
ú
ú
û
ù
ê
ê
ë
é
+ or [ ] 2
2
0
2
0
v
v
kt
v
2
1 =
+
or
kt
v
2
1
v
v
or
kt
v
2
1
v
v
2
0
0
2
0
2
0
2
+
=
+
=
21. (d) )
e
1
1
(
b
a
)
e
1
(
b
a
)
e
1
(
b
a
x 1
b
1
b
-
=
-
=
-
= -
´
-
a (e 1)
b e
-
= b
/
a
3
2
~
b
a
637
.
0
718
.
2
)
718
.
1
(
b
a
718
.
2
)
1
718
.
2
(
b
a
-
=
=
-
=
velocity bt
ae
dt
dx
v -
=
= , v0 = a
accleration ab
a
&
abe
dt
dv
a 0
bt
-
=
-
=
= -
At t = 0, 0
)
1
1
(
b
a
x =
-
= and
At
b
1
t = , b
/
a
3
2
)
e
1
1
(
b
a
)
e
1
(
b
a
x 1
=
-
=
-
= -
At
a
t , x
b
= ¥ =
It cannot go beyond this, so point
a
x
b
> is not reached
by the particle.
At t = 0, x = 0, at
a
t , x
b
= ¥ = , therefore the particle
does not come back to its starting point at ¥
=
t .
22. (c) 2
x t 2t 1
= + +
Hence
dx
v 2t 2
dt
= = + . It increases with time.
23. (b) When a body falls through a height h, it acquires a
velocity gh
2 .
24. (c) Initial relative velocity vA – vB, is reduced to 0 in
distance d¢ (<d) with retardation a.
d
a
2
)
v
v
(
0 2
B
A
2
¢
-
=
-
-
2 2
A B A B
(v v ) (v v )
d d
2a 2a
- -
= >
¢
25. (d)
EXERCISE -2
1. (c) Given that x = At2 – B t3
velocity
2
dx
2At 3Bt
dt
= = -
and acceleration Bt
6
A
2
dt
dx
dt
d
-
=
÷
ø
ö
ç
è
æ
=
For acceleration to be zero 2A – 6Bt = 0.
B
3
A
B
6
A
2
t =
=
2. (a) t
sin
s
dt
x
d
a 2
2
2
w
w
-
=
=
On integrating, t
cos
s
t
cos
s
dt
dx 2
w
w
=
w
w
w
=
Again on integrating, we get
t
sin
s
t
sin
s
x w
=
w
w
w
=
3. (c) 3
dy
v b 2ct 4d t
dt
= = + -
3
0
v b 2c(0) 4d(0) b
= + - =
(Q for initial velocity, t = 0)
Now 2
dv
a 2c 12d t
dt
= = -
2
0
a 2c 12d(0) 2c
= - = , (at t = 0)
4. (d) 1 2
1 2
2 1
1 2 1 2
x x
2v v
1
2 2
x x v v
v v
2v 2v 2v v
+
= =
+
æ ö
+
+ ç ÷
è ø
5. (b) Let u be the initial velocity
1 1 2 1 2
v u a t , v u a (t t )
¢ ¢
= + = + +
and 3 1 2 3
v u a (t t t )
¢ = + + +
Now 1 1
1
u v u (u a t )
v
2 2
¢
+ + +
= = 1
t
a
2
1
u +
=
1 2
2 1 2
v v 1
v u a t a t
2 2
¢ ¢
+
= = + +
2 3
3 1 2 3
v v 1
v u a t a t a t
2 2
¢ ¢
+
= = + + +
So, 1 2 1 2
1
v v a (t t )
2
- = - +
and 2 3 2 3
1
v v a (t t )
2
- = - +
1 2 2 3 1 2 2 3
(v v ) :(v v ) (t t ) :(t t )
- - = + +](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-61-320.jpg)

![59
Motionina Straight Line
16. (b) The stone rises up till its vertical velocity is zero and
again reached the top of the tower with a speed u
(downward). The speed of the stone at the base is 3u.
–
+
v, g, h
u
Hence
2
2 2 4u
(3u) ( u) 2gh or h
g
= - + =
17. (c) Sobysecond equation ofmotion, we get
2
1
S ut at
2
= +
here S = l, u = 0, a = g sinq
2
2 2h 1 2h
t
a sin g
gsin
= = =
q
q
l h
sin
æ ö
q =
ç ÷
è ø
Q
l
h
g
cosq
g
sinq
g
q
18. (a) S = ut + ½at2 here a = g
For first body u1 =0 Þ S1=½g × 9
For second body u2=0 Þ S2= ½g × 4
So difference between them after 3 sec. = S1 – S2
= ½ g×5
If g = 10m/sec2 then S1–S2 = 25 m.
19. (b) Relative speed of each train with respect to each other
be, n = 10 + 15 = 25 m/s
Here distance covered by each train = sum of their
lengths= 50 + 50 = 100 m
Required time .
sec
4
25
100
=
=
20. (d) At highest point of the trajectory velocity becomes
zero and all kinetic energychanges to potential energy
so at highest point, K.E. = 0
21. (b) The distance travel in nth second is
Sn = u + ½ (2n–1)a ....(1)
so distance travel in tth & (t+1)th second are
St = u +½ (2t–1)a ....(2)
St+1= u+½ (2t+1)a ....(3)
As per question,
St+St+1 = 100 = 2(u + at) ....(4)
Now from first equation of motion the velocity, of
particle after time t, ifit moves with an accleration a is
v = u + a t ....(5)
where u is initial velocity
Sofrom eq(4) and (5), we get v = 50cm./sec.
22. (b) Since v2 = u2 + 2as
For first case u1=20m/sec, v1= 0, a1= g = 10, s1= ?
So m
20
10
2
400
s1 =
´
=
For second case (at moon) u2 =20m/sec, v2=0,
?
s
,
sec
/
m
7
.
1
6
g
a 2
2
2 =
=
=
6
/
10
2
400
7
.
1
2
400
s2
´
=
´
= so
6
1
s
s
2
1
=
23. (d) All options are correct :
(i) When two bodies A & B move in opposite
directions then relative velocity between A & B
either VAB or VBA both are greater than VA&VB.
(ii) When twobodiesA& Bmove in parallel direction
then A
AB
B
A
AB V
V
V
V
V <
Þ
-
=
B
BA
A
B
BA V
V
V
V
V <
Þ
-
=
24. (b) From third equation of motion
v2 = u2 – 2gh ( a g)
= -
Q
Given, v = 10 m/sec at h/2. But v = 0, when particle
attainedmaximum height h.
Therefore (10)2 = u2 – 2gh/2
or 100 = 2gh –2gh/2 (Q0 = u2 – 2gh)
Þ h = 10m
25. (b) Since in both case the height of building and down
ward acceleration ‘g’ is same. So both stones reach
simultaneouslyi.e.,
2
2
t
10
2
1
10
gt
2
1
S ´
=
Þ
=
or t 2 sec,
= for both stone.
26. (d) Speed 1
5
v 60
18
= ´ m/s
50
3
= m/s
= = ´ =
1 1
5 100
d 20m, v' 120
18 3
m/s
Let dceleration be a
2
1 1
0 v 2ad
= - ....(1)
or 2
1 1
v 2ad
=
2
1 2
(2v ) 2ad
= ...(2)
(2) divided by (1) gives,
m
80
20
4
d
d
d
4 2
1
2
=
´
=
Þ
=
27. (d) Equation of motion is at
u =
we know that ds
u
dt
= at
dt
ds =
Þ atdt
ds
or =
integrating it we get, ò
=
ò
4
0
s
0 tdt
a
ds
a
8
]
t
[
2
a
s 4
0
2
=
=
28. (d) The onlyforce acting on the ball is the force ofgravity.
The ball will ascend until gravity reduces its velocity
to zero and then it will descend. Find the time it takes
for the ball toreach its maximumheight and then double
the time to cover the round trip.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-63-320.jpg)

![61
Motionina Straight Line
45. (c) 1
(8 1 3 1 1) 0
v 5ms
1
-
´ - ´ ´ -
= =
46. (c) Sincethe initial velocityofjump issame on both planets
So 0 = u2– 2gAhA
0 = u2–2gBhB
or m
18
2
1
9
h
h
g
h
g
B
B
B
A
A
=
´
=
Þ
=
´
47. (d)
q
S
R
P Q
mg
q
sin
m
g
q
cos
mg
Let distance (PR) iscovered by the particle in time ‘t’.
Þ PR = q
=
q
+ sin
gt
2
1
t
.
sin
g
2
1
0 2
2
Further PR =
q
cos
PQ
(Given PQ = constant)
Þ PQ = q
qcos
sin
gt
2
1 2
= q
2
sin
gt
4
1 2
Þ t = 2
q
2
sin
g
PQ
q
µ
2
sin
1
t
So as q increases, q
2
sin first increases and then
decreases. Hence ‘t’ first decreases and then increases.
48. (d) Given x = ae–at + bebt
Velocity, v =
dx
dt
= –aae–at + bbebt = - +
a
e
b e
t
t
a
b
a
b
i.e., goon increasing with time.
49. (b) 2
y t ; v- t';a t°
µ µ µ
50. (c) On differentiating, acceleration = 0.2t )
t
(
f
a =
Þ
51. (d) Use v2 – u2 = 2aS. In both the cases, (u positive or
negative) u2 is positive.
52. (b) Area under a-t graph is change in velocity.
Area
1 1 1
(4 4) 6 4 2 4 2 2
2 2 2
= ´ + ´ + ´ ´ - ´ ´
1
36 2 34 ms-
= - =
As initial velocity is zero therefore, the velocity at 14
second is 1
s
m
34 - .
53. (c) At t = 20s, d = 20 m
54. (a) At six points in the graph the tangents have zero slope
i.e. velocity is zero.
55. (d) Time fall is
1
second.
2
2
1 1 10
h g
2 2 8
æ ö
= =
ç ÷
è ø
=1.25m
56. (b)
3
2
1
av
t
t
t
x
3
x
2
x
v
+
+
+
+
=
1
max
2x
t
v
= , 2
max
2x
t
v
= , 3
max
6x
t
v
=
max
av
6x v
v
10x
=
av
max
v 3
v 5
=
57. (c) Let A
v and B
v are the velocities of two bodies.
In first case, A
v + B
v = 6m/s ........(1)
In second case, A
v – B
v = 4m/s .........(2)
From (1) &(2) we get, A
v = 5 m/s and B
v =1 m/s.
58. (d) BB
v
r
= Relative velocityofballw.r.t. balloon = v
u +
gt
)
v
u
(
0 +
+
-
= of
g
v
u
t
+
=
Total time
g
)
v
u
(
2 +
=
59. (c) 2
2
2
1 )
N
n
(
g
2
1
y
,
gn
2
1
y -
=
=
]
)
N
n
(
n
[
g
2
1
y
y 2
2
2
1 -
-
=
-
Þ
g
1 (2n N)N
2
= - ]
1
y
y
[ 2
1 =
-
Q
Þ
2
N
gN
1
n +
=
60. (b) S1 =
2
1
g
2
2
1
÷
ø
ö
ç
è
æ
, S1 + S2 =
1
2
g(1)2
2
1
g
2
2
3
÷
ø
ö
ç
è
æ
= S1 + S2 + S3
By solving we get
S1 : S2 : S3 = 1 : 3 : 5
61. (b) Distance in last two second
=
2
1
×10× 2 =10m.
Total distance =
2
1
× 10 × (6 + 2) = 40 m.
62. (d) In (a), at the same time particlehas twopositionswhich
is not possible. In (b), particle has two velocities at the
same time. In (c), speed is negative which is not
possible.
63. (a) Velocityat timet is tan 45° = 1.Velocityat time(t = 1) is
tan 60 3
° = . Acceleration is change in velocity in
one second = 3 1
- .
64. (c) Here, the particle B moves upwards. Let the upward
velocity of B be v then
v
tan 60
10
= °](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-65-320.jpg)

![63
Motionina Straight Line
75. (b) v u at
= +
r r r
ˆ ˆ ˆ ˆ
(2 3 ) (0.3 0.2 ) 10
v i j i j
= + + + ´ = ˆ ˆ
5 5
i j
+
| |
v
r
= 2 2
5 5
+ ; | | 5 2
v =
r
76. (a) Q h =
1
2
gt2
h1 =
1
2
g(5)2 = 125
h1 + h2 =
1
2
g(10)2 = 500
Þ h2 = 375
h1 + h2 + h3 =
1
2
g(15)2 = 1125
Þ h3 = 625
h2 = 3h1 , h3 = 5h1
or h1 =
2
h
3
=
3
h
5
77. (a) h =
2
gT
2
1
now for t = T/3 second vertical distance moved is given by
h¢
2
1 T
g
2 3
æ ö
= ç ÷
è ø
Þ h¢
2
1 gT h
2 9 9
= ´ =
position of ball from ground
9
h
h -
=
9
h
8
=
78. (d) x = a + bt2 = 15 + 3t2
v =
dx
dt
= 3 × 2t = 6t
Þ t 3s
v = = 6 × 3 = 18cm/s
79. (a) Motion with constant acceleration is represented by a
quadratic equation of t
Y = (p + qt) (r + pt) = pr + qrt + p2t + pqt2
80. (c) Let the maximum height attained bythe ball be h.
At maximum height , velocityof ball, v = 0
Given, initial velocity, u = 19.6 m/s
Using the equation of motion,
v2 = u2 + 2gh
We get 0= (19.6)2 + 2 (–9.8) ×h
Þ h =
2
(19.6)
2 9.8
´
= 19.6m
81. (a) Here, length of train A, LA = 120 m
length of train B, LB = 130 m
velocity of train A, vA = 20 m/s
velocity of train B, vB = 30 m/s
Train B is running in opposite direction to train B,
velocityof train B relative to train A,
vBA = vB + vA
= (30 + 20) m/s
= 50 m/s
Total distance to be covered by train B
= LA +LB=(120+130)m
=250m
Hence, time required by train B to cross train A
t =
250
50
sec = 5sec
82. (a) Retardation,
2 2 2
0 (25/3)
2 2 8
v u
a
s
- -
= =
´
2
1
25
16
3
a
æ ö
= - ´
ç ÷
è ø
For u = 60 km h–1 =
50
3
ms–1
2
2
0 (50/ 3)
2 [ (25/3) 1/16]
s
-
=
´ - ´
=32m
83. (d) Velocitytime curve will be a straight line as shown:
o
t
v
At the highest point v = 0.
84. (b) Let O be the origin, then
O
Q
N
Car
E
Train P
N
W
S
E
passenger in the train at P observes the car at Q along
the direction PQ; i.e. west north direction.
85. (d) Given : u = 0, t = 5 sec, v= 108 km/hr = 30m/s
By eqn of motion
v = u + at
or 2
v 30
a 6 m / s [ u 0]
t 5
= = = =
Q
2
1
1
S at
2
=
2
1
6 5 75 m
2
= ´ ´ =
Distance travelled in first 5 sec is 75m.
Distance travelled with uniform speed of 30 m/s is S2
395 = S1 + S2 + S3
395 = 75+ S2 +45
S2 =395–120= 275m
Timetaken to travel 275 m =
275
9.2sec
30
=
For retarding motion, we have
02 – 302 = 2 (– a) × 45](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-67-320.jpg)
![64 PHYSICS
We get, a = 10 m/s2
Now by, S = ut +
2
1
at
2
45 = 30t +
2
1
(–10)t
2
45 = 30t – 5t2
Pn solving we get, t = 3 sec
Total time taken = 5 + 9.2 +3 = 17.2 sec.
86. (c) When particle comes to rest,
V = 0 =
dx d
dt dt
= (40 + 12t – t3)
Þ 12 – 3t2 = 0
Þ t2 =
12
4
3
= t = 2 sec
Therefore distance travelled byparticle before coming
to rest,
x = 40+ 12t – t3 = 40 + 12 × 2 – (2)3 = 56m
87. (b) We get acceleration by double differentiation of
displacement.
V=
1 2
0
a t a
dx d
a t
dt dt 2 3
2
æ ö
= + -
ç ÷
è ø
= 1
2
a 2
a t
2 3
-
a =
1
2
2
a 2
d a t
dv 2
2 3
a
dt dt 3
æ ö
-
ç ÷
è ø -
= =
88. (b)
1 1 1
(2 4) 2 1 4 3 4 2m
2 2 2
+ ´ + ´ ´ - ´ ´ =
89. (a) Velocity of boat 1
h
km
8
2
8
8 -
=
+
=
Velocityof water 1
h
km
4 -
=
160
h
3
8
4
8
8
4
8
8
t =
=
+
+
-
= minute
90. (b) Using relative terms
s
/
m
0
u .
rel =
?
t
,
m
9
.
4
S
,
s
m
8
.
9
a 2
=
=
= -
2
t
8
.
9
2
1
t
0
9
.
4 ´
´
+
´
=
Þ 9
.
4
t
9
.
4 2
= Þ t = 1 s
91. (b) From first equation of motion v = u + a t
here u = 40, a = g = – 10, t = 2
so v = 40 – 10 × 2 = 20 m/sec
92. (b) v= [144 × 1000/(60 × 60)] m/sec.
v = u + at
or (144 ×1000)/(60 ×60) =0+ a ×20
2
144 1000
a 2m / sec
60 60 20
´
= =
´ ´
Now
2
1
s u t at
2
= + m
400
)
20
(
2
2
1
0 2
=
´
´
+
=
93. (c) Height of tap = 5m and (g) = 10 m/sec2.
For the first drop, 5 = ut
2
1
2
+ gt
2
1
(0 ) 10
2
= ´ + ´
t t = 5t2 or t2 = 1 or t = 1 sec.
It means that the third drop leaves after one second of
the first drop. Or, each drop leaves after every 0.5 sec.
Distance covered by the second drop in 0.5 sec
2
1 1
(0 0.5) 10
2 2
= + = ´ + ´
ut gt ×(0.5)2
=1.25m.
Therefore, distance of the second drop above the
ground = 5 – 1.25 = 3.75 m.
94. (d) At E, the slope of the curve is negative.
95. (d) Velocity, 2
3 –12 3
= = +
ds
v t t
dt
Acceleration, 6 –12;
= =
dv
a t
dt
For a = 0, we have,
0 = 6 t – 12 or t = 2s. Hence, at t = 2 s the velocitywill be
2 –1
3 2 –12 2 3 9 ms
= ´ ´ + = -
v
96. (a) 4
3
0 (2 4 1)
7
2
5
0 (2 3 1)
2
+ ´ -
= =
+ ´ -
a
D
a
D
97. (b) In one dimensional motion, thebodycan have at a time
one velocity but not two values of velocities.
98. (d) Inuniformmotion theobject moveswithuniformvelocity,
the magnitude of its velocity at different instane i.e., at
t = 0, t =1, sec, t =2sec..... will alwaysbeconstant. Thus
velocity-timegraphfor an objectinuniform motion along
a straight path isa straight lineparallelto timeaxis.
99. (b) 100. (d)
EXERCISE -3
Exemplar Questions
1. (b) Ifwe draw a line parallel to time axis from the point (A)
on graph at t = 0 sec. This line can intersect graph at B.
In graph (b) for one value of displacement there are
twodifferent pointsoftime. so, for onetime, the average
velocity is positive and for other time is equivalent
negative.
As there are opposite velocities in the inteval 0 to T
hence average velocity can vanish in (b). This can be
seen in the figure given below.
t
x
O
A B
T
Here, OA = BT (same displacement) for two different
points of time.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-68-320.jpg)
![65
Motionina Straight Line
2. (a) As the lift is moving downward directions so
displacement isnegative (zero).Wehavetoseewhether
the motion is accelerating or retarding.
Dueto downward motion displacement is negative the
lift reaches 4th floor is about to stop hence, motion is
retarding (–a) downward in nature hence, x < 0; a > 0.
8th floor
x < 0
4th floor
Ground floor
x < 0 O
6th floor
As displacement is in negative direction,
x < 0 velocity will also be negative i.e., v < 0 but net
acceleration is +ve a > 0, that can be shown in the
graph.
3. (b) In one dimensional motion, for the maximum and
minimum displacement we must have the magnitude
and direction of maximum velocity.
As maximum velocityin positive direction is v0, hence
maximum velocity in opposite direction is also –v0.
Maximum displacement in one direction = v0T
Maximum displacement in opposite directions = –v0T.
Hence, 0 0
- < <
v T x v T
4. (c) Time taken totravel first half distance,
1
1 1
/ 2
2
= =
l l
t
v v 1
( / 2)
=
QL l
Time taken to travel second half distance,
2
2
2
=
l
t
v 2
( / 2)
=
QL l
So, total time taken to travel full distance
= t1 + t2
1 2 1 2
1 1
2 2 2
é ù
= + = +
ê ú
ë û
l l l
v v v v
Total time
2 1
1 2
2
é ù
+
= ê ú
ë û
v v
l
v v
So, average speed,
vav. =
Total distance
Total time
=
1 2
av.
1 2
1 2
2
1 1
2
Þ = =
+
é ù
+
ê ú
ë û
v v
l
v
v v
l
v v
1 2
av.
1 2
2
=
+
v v
v
v v
5. (b) As given that, x = (t – 2)2
Now, velocity
2
( 2)
= = -
dx d
v t
dt dt
= 2 (t – 2) m/s
Acceleration, [2( 2)]
= = -
dv d
a t
dt dt
= 2[1–0]=2m/s2 =2ms–2
at t = 0; v0 = 2 (0 – 2) = –4 m/s
t = 2 s; v2 = 2 (2 – 2) = 0 m/s
t = 4 s; v4 = 2 (4 – 2) = 4 m/s
B
D
O A
V
t
4
2
C
–4 m/s
4 m/s
(Time)
v-t graph is shown in diagram.
Distance travelled
= area between time axis of the graph
= area OAC + are ABD
1 1
2 2
= ´ + ´
OA OC AD BD
4 2 1
2 4 8 m
2 2
´
= + ´ ´ =
If displacement occurs
1 1
2 2
= ´ ´ + ´ ´
OA OC AD BD
1 1
2( 4) 2 4 0
2 2
= ´ - + ´ ´ =
6. (c) Let us consider, displacement is L, then
velocity of girl with respect to ground,
1
=
g
L
v
t
Velocity of escalator with respect to ground,
2
=
e
L
v
t
Net velocityof the girl on moving escalator with respect
to ground
1 2
= + = +
g e
L L
v v
t t
Þ vge
1 2
1 2
é ù
+
= ê ú
ë û
t t
L
t t](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-69-320.jpg)






![72 PHYSICS
3. . .
A B B A
=
r r
r r
Dot product of two vectors is commutative.
4. 2
.
A A A
=
r r
5. .( ) . .
A B C A B A C
+ = +
r r r r r
r r
Dot product is distributive.
6. x y z x y z
ˆ ˆ ˆ ˆ ˆ ˆ
A.B (A i A j A k).(B i B j B k)
= + + + +
r r
= (Ax Bx + Ay By + Az Bz)
Vector or Cross Product
The vector product of two vectors is defined as a vector having
magnitude equal to the product of two vectors and sine of the
angle between them. Its direction is perpendicular to the plane
containing the two vectors (direction of the vector is given by
right hand screw rule or right hand thumbrule.
C A B
= ´
u
r ur u
r
= (AB sin q) n̂
The direction of (A B)
´
ur u
r
perpendicular to the plane containing
vectors A
ur
and B
u
r
in the sense of advance of a right handed
screw rotated from A
ur
to B
u
r
is through the smaller angle between
them.
( )
A B C
´ =
ur u
r u
r q
B
A
e.g., ; ;
v r r F L r p
= w´ t = ´ = ´
r r
r
r r r r r r
Properties of Vector or Cross Product
1. ˆ ˆ
ˆ ˆ ˆ ˆ 0
i i j j k k
´ = ´ = ´ =
2. ˆ ˆ ˆ
ˆ ˆ ˆ ˆ ˆ ˆ
; ;
i j k j k i k i j
´ = ´ = ´ =
i
j
k
3. 0
A A
´ =
r r
4. A B B A
´ ¹ ´
r r
r r
(not commutative) [ ]
´ = - ´
r r
r r
Q A B B A
5. ( ) ( ) ( )
A B C A B A C
´ + = ´ + ´
r r r r r
r r
(followsdistributivelaw)
6. ˆ ˆ
ˆ ˆ ˆ ˆ
( ) ( )
x y z x y z
A B A i A j A k B i B j B k
´ = + + ´ + +
r r
x y z
x y z
ˆ ˆ ˆ
i j k
A A A
B B B
=
= (Ay Bz – Az By) î + (Az Bx – A
Ax Bz) ĵ
+ (Ax By – Ay Bx) k̂
7. The cross product of two vectors represents the area of the
parallelogram formed bythem.
k
q
A
B
P Q
R
S
| | ( sin )
A B A B
´ = q
r r
= area ofparallelogram PQRS
= 2 (area of DPQR)
8. A unit vector which is perpendicular to A as well as B is
sin
| |
´ ´
=
q
´
uu
r uu
r r r
uu
r uu
r
A B A B
AB
A B
Keep in Memory
1.
x x y y z z
2 2 2 2 2 2
x y z x y z
A B A B A B A.B
cos
| A || B |
A A A B B B
+ +
q = =
+ + + +
ur u
r
ur u
r
2. tan q =
q
q
=
´
cos
B
A
sin
B
A
B
.
A
|
B
A
|
r
r
r
r
3.
2 2 2 2
.
| A B | | A B| A B
´ + =
r r
r r
4. |
)
A
(
)
B
(
|
2
|
B
–
A
|
|
B
A
|
r
r
r
r
r
r
´
=
´
+
5. If 0
C
B
A =
+
+
r
r
r
, then A
C
C
B
B
A
r
r
r
r
r
r
´
=
´
=
´
6. q
=
´
- 2
cos
B
A
|
B
A
|
|
B
.
A
| 2
2
2
2
r
r
r
r
7. If B
.
A
|
B
A
| =
´ then angle between A and B is
4
p
.
8. If B
||
A then 0
B
A =
´
9. Division by a vector is not defined. Because, it is not
possible to divide by a direction.
10. The sum and product of vectors is independent of
co-ordinate axes system.
CONDITION OF ZERORESULTANT VECTOR AND LAMI'S
THEOREM
If the three vectors acting on a point object at the same time are
represented in magnitude and direction by the three sides of a
triangle taken in order, then their resultant is zero and the three
vectors are said tobe in equilibrium.
i.e. 1 2 3
F F F 0
+ + =
r r r](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-76-320.jpg)
![73
Motion in a Plane
P Q
R
F3 F2
F1
a
b g
Lami's Theorem
It states that if three forces acting at a point are in equilibrium,
then each force is proportional to the sine of the angle between
the other two forces.
3
1 2 F
F F
sin sin sin
= =
a b g
r
r r
F3
F1
F2
a
b
g
or,
3
1 2 F
F F
PQ QR PR
= =
r
r r
Example10.
Calculate the area of a parallelogram formed from the
vectors k̂
3
ĵ
2
î
A +
+
=
r
and k̂
j
3
î
2
B +
-
=
r
, as adjacent
sides.
Solution :
The area of a parallelogram is given by |
B
A
|
r
r
´
Here,
ˆ ˆ ˆ
i j k
A B 1 2 3
2 3 1
´ = +
-
r r
= î [(2 × 1) – (–3 × 3)] + ĵ [(3 × 2) – (1 × 1)]
+ k̂ [(1 × –3)– (2 × 2)]
= 11 î + 5 ĵ – 7 k̂
2 2 2
| A B | (11) (5) ( 7)
´ = + + -
ur u
r
@ 14
Example11.
A particle suffers three displacements 4m in the northward,
2 m in the south-east and 1 m in the south-west directions.
What is the displacement of the particle and the distance
covered by it?
Solution :
Taking a frame of reference with the x-axis in the eastward
and the y-axisin the northward direction
Y
North (N)
X East (E)
West (W)
South (S)
1 2
ˆ ˆ ˆ
s = 4j, s = 2cos 45ºi 2 sin 45º j
-
ur uu
r
3
ˆ ˆ
s = 2 cos 45º i 2 sin 45º j
- -
uu
r
1 2 3
ˆ ˆ ˆ ˆ ˆ
s = s +s +s = 4j+ 2 i 2 j 2 i 2 j
- - -
r ur uu
r uu
r
Displacement ˆ
s (4 2 2)j
= -
r ˆ
= (1.17)j= (1.17)
(northward)
And total distance covered = 4 + 2 + 1 = 7m
Example12.
Prove that vectors ˆ
ˆ ˆ
A= i +2j+3k
r
and ˆ ˆ
B = 2i j
-
r
are
perpendicular to each other.
Solution :
Here, k̂
3
ĵ
2
î
A +
+
=
r
and ĵ
î
2
B -
=
r
Two vectors are perpendicular to each other if, 0
B
.
A =
r
r
Now B
.
A
r
r
= )
k̂
3
ĵ
2
î
( +
+ . )
ĵ
î
2
( - = 0
= 1 × 2+ 2 × (–1) + 3 ×(0) = 2 – 2+ 0 = 0
Since 0
B
.
A =
r
r
, therefore vectors A
r
and B
r
are
perpendicular to each other.
Example13.
Find the angle between the vectors ˆ
ˆ ˆ
A i j 2k
= + -
r
and
ˆ
ˆ ˆ
B i 2 j k
= - + -
r
.
Solution :
Here k̂
2
ĵ
î
A -
+
=
r
, k̂
ĵ
2
î
B -
+
-
=
r
We know that q
= cos
AB
B
.
A
r
r
or
AB
B
.
A
cos
r
r
=
q
Now 2 2 2
2 2 2
A 1 1 ( 2) 6 ,
B ( 1) 2 ( 1) 6
ˆ ˆ ˆ ˆ ˆ ˆ
A.B (i j 2k).( i 2j k) 1 2 3 3
3 3 1
cos or 60
6 2
6 6
= + + - =
= - + + - =
= + - - + - = - + + =
q = = = q = °
´
r r
Example14.
A particleis displaced from a point (3, – 4, 5) toanother point
(–2, 6, – 4) under a force k̂
ĵ
3
î
2 -
+ . Find the work doneby
the force.
Solution :
k̂
ĵ
3
î
2
F -
+
=
r
The displacement of the particle is
s
r = position vector of point (–2, 6, – 4) – position vector of
point (3, – 4, 5)
s
r = k̂
9
ĵ
10
î
5
)
k̂
5
ĵ
4
î
3
(
)
k̂
4
ĵ
6
î
2
( -
+
-
=
+
-
-
-
+
-](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-77-320.jpg)



![77
Motion in a Plane
Solution : (a)
Refer to fig., the boat man should go along OC in order to
cross the river straight (i.e. along OB).
B
C
O A
2km
q
b
n
r
n
º
30
sin
2
1
10
5
OC
CB
sin
b
r
=
=
=
n
n
=
=
q ; q = 30º;
Boat man should go along in a direction inclined at
90º + 30º = 120º to the direction of river flow.
Example18.
A man swims at an angle q = 120º to the direction of water
flow with a speed vmw = 5km/hr relative to water. If the
speed of water vw = 3km/hr, find the speed of the man.
Solution :
r
v mw = r
v m – r
v w
r
v m = r
v mw + r
v w
Þ vm = | r
v mw + r
v w| = v v v v
mw w mw w
2 2
2
+ + . cosq
Þ vm = 5 3 2 5 3 120
2 2
+ + ( )( )cos º
Þ vm = 25 9 15
+ - = 19 m/sec.
Example19.
A gun throws a shell with a muzzle speed of 98 m/sec. When
the elevation is 45º, the range is found to be 900 m. How
much is the range decreased by air resistance?
Solution :
Without air resistance, the expected range
8
.
9
)
98
(
8
.
9
90
sin
)
98
(
g
2
sin
u
R
2
2
2
=
´
=
q
= =980m
Decrease in range = 980 m – 900 m = 80 m
Example20.
A particle is projected with velocity u at an angle q with
the horizontal so that its horizontal range is twice the
greatest height attained. The horizontal range is
(a) u2/g (b) 2 u2/3 g
(c) 4 u2/5 g (d) None of these
Solution : (c)
Greatest height attained
g
2
sin
u
H
2
2
q
= ……(1)
Horizontal range,
g
cos
sin
u
2
g
2
sin
u
R
2
2
q
q
=
q
= ……(2)
[Qsin 2q = 2 sin q cosq]
Given that R = 2 H
g
2
sin
u
2
g
cos
sin
u
2 2
2
2
q
=
q
q
Solving we get tan q = 2 .....(3)
Hence )
5
/
1
(
cos
and
)
5
/
2
(
sin =
q
=
q
From eqn. (2)
g
5
u
4
5
1
5
2
g
u
2
R
2
2
=
´
´
=
Example21.
A body is projected downwards at an angle of 30º to the
horizontal with a velocity of 9.8 m/s from the top of a tower
29.4 m high. How long will it take before striking the
ground?
Solution :
The situation is shown in fig.
30°
u
B
A
–
+
The time taken bythe bodyis equal to the time taken bythe
freelyfalling bodyfrom the height 29.4m with initial velocity
u sin q. This is given by
9.8
usin 4.9 m / s
2
q = =
Applying the formula, s = u t +
2
1
g t2, we have
29.4 = 4.9 t +
2
1
(9.8) t2 or 4.9 t2 + 4.9 t – 29.4 = 0
(because s, u and g are all in downward direction)
t2 + t – 6 = 0or t = 2 or –3
Time taken to reach ground = 2 second
Example22.
Two boys stationed at A and B fire bullets simultaneously
at a bird stationed at C. The bullets are fired from A and B
at angles of 53° and 37° with the vertical. Both the bullets
fire the bird simultaneously. What is the value of vA if
vB = 60 units? (Given : tan 37° = 3/4)
Solution :
The vertical components must be equal.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-81-320.jpg)
![78 PHYSICS
vA cos 53° = vB cos 37°
or vA = vB
cos 37
cos (90 37 )
°
° - °
or vA = 60 cot 37° =
60
tan 37° [QvB = 60 units]
=
60 4
3
´
= 80 units
PROJECTILE ON AN INCLINED PLANE
Let a body is thrown from a plane OA inclined at an angle a with
the horizontal, with a constant velocity u in a direction making an
angle q with the horizontal.
The body returns back on the same plane OA. Hence the net
displacement of the particle in a direction normal to the plane OA
is zero.
a
q
(q-a)
g sin( )
a
g cos( )
a
O
A
B
u a
g
y
uy
x
ux = u cos (q – a ) along the incline, + x-axis)
uy = u sin (q – a ) along the incline, + y-axis)
ax = g sin a along – x-axis, as retardation
ay = g cos a along – y-axis, as retardation
The time of flight of the projectile is given by
2
at
2
1
ut
s +
=
or 2
1
0 u sin( )T g cos T
2
= q - a - a
usin( )
T
gcos( )
2 q - a
=
a
If maximumheight above the inclined plane is H,
2 2
u sin ( )
H
2g
q - a
=
The horizontal range R of the projectile is given by
OB = u cos q t =
2
u sin( )cos
R
gcos
2 q - a q
=
a
The range of the projectile at the inclined plane is given by
OA=
2
2
OB u sin( )cos
R
cos gcos
2 q- a q
= =
a a
Condition for horizontal range R on the inclined plane to be
maximum:
Since
2
2
u
R [2sin( )cos ]
gcos
= q - a q
a
2
2
u
[sin(2 ) sin ]
gcos
= q - a - a
a
{2 sin Acos B = sin(A+B)+sin(A–B)}
R is maximumwhen sin (2q –a) is maximum
i.e., sin (2q – a) =1 or
4 2
p a
q = +
2
max 2
u
R [1 sin ]
gcos
Þ = - a
a
or Rmax(on inclined plane) max
R (on horizontalplane)
1 sin
=
+ a
where Rmax (on horizontal plane)
g
2
u2
= .
Conditionfor time offlightTto bemaximum:
2 u sin( )
T
g cos
q - a
=
a
so T is max when sin (q – a) is maximum
i.e., sin (q –a) = 1 or
2u
T
2 g cos
p
q = + a Þ =
a
Itmeans that ifq1 istheanglefor projectilefor which Tismaximum
and q2 isthe anglefor which Rismaximum, then q1 = 2q2.
Example23.
The slopes of wind screen of two cars are b1 = 30° and
b2 = 15° respectively. At what ratio v1/v2 of the velocities
of the cars will their drivers see the hailstorms bounced by
windscreen of their cars in the vertical direction? Assume
hailstorms falling vertically.
Solution :
From the fig tan
1
v
v
a = and 1
90 2
a = °- b
where v is velocity of hail
1 1
1
v
tan(90 2 ) cot 2
v
° - b = b =
b1
–v1
b1
b1
v
a
Similarly, 2
2
v
cot 2
v
b =
1 2
2 1
v cot 2 cot30
3.
v cot 2 cot 60
b
= = =
b](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-82-320.jpg)





![85
Motion in a Plane
26. The magnitude of the vector product of two vectors is 3
times the scalar product. The angle between vectors is
(a)
4
p
(b)
6
p
(c)
3
p
(d)
2
p
27. IfA= B + C and the magnitudes ofA, B and C are5, 4 and 3
units, the angle between A and C is
(a) cos–1 (3/5) (b) cos–1 (4/5)
(c)
2
p
(d) sin–1 (3/4)
28. A rectangular sheet of material has a width of 3 m and a
length of 4 m. Forces with magnitudes of 3 N and 4N.
respectively, are applied parallel to two edges of the sheet,
as shown in the figure below.
3m
4m
4N
3N
F
q
Athird force F, is applied to the centre of the sheet, along a
line in the plane of the sheet, at an angle q = tan 0.75 with
respect to the horizontal direction. The sheet will be in
translational equilibrium when F has what value?
(a) F = 3 N (b) F= 4N
(c) F = 5 N (d) F= 7N
29. The linear velocityof a rotating body is given by :
v r
= w ´
uu
r uu
r ur
If k̂
3
ĵ
4
r
and
k̂
2
j
ˆ
2
î -
=
+
-
=
w , then the magnitude of
v is
(a) units
29 (b) units
31
(c) units
37 (d) units
41
30. Two forces are such that the sum of their magnitudes is 18 N
and their resultant is 12 N which is perpendicular to the
smaller force. Then the magnitudes of the forces are
(a) 12 N, 6 N (b) 13 N, 5 N
(c) 10 N, 8 N (d) 16N, 2N.
31. For any two vectors A
r
and B
r
, if A . B | A B |
= ´
r r
r r
, the
magnitude of C A B
= +
r r r
is
(a) A+ B (b) AB
2
B
A 2
2
+
+
(c) 2
2
B
A + (d)
2
AB
B
A2
+
+ 2
32. The angles which the vector ˆ ˆ ˆ
A 3i 6j 2k
= + +
r
makes with
the co-ordinate axes are :
(a)
7
1
cos
,
7
4
cos
,
7
3
cos 1
1
1 -
-
-
(b)
7
2
cos
,
7
6
cos
,
7
3
cos 1
1
1 -
-
-
(c)
7
3
cos
,
7
5
cos
,
7
4
cos 1
1
1 -
-
-
(d) None of these
33. The resultant of two forces 3P and 2P is R. If the first force
is doubled then the resultant is also doubled. The angle
between the two forces is
(a) 60º (b) 120º
(c) 70º (d) 180º
34. Let C A B
= +
r r r
(a) | C |
r
is always greater than | A |
r
(b) It is possible to have | C | | A |
<
r r
and | C | | B |
<
r r
(c) C
r
is always equal to A B
+
r r
(d) C
r
is never equal to A B
+
r r
35. At what angle must the two forces (x + y) and (x – y) act so
that the resultant may be 2 2
(x y )
+ ?
(a) 1 2 2 2 2
cos [ (x y )/ 2(x y )]
-
- + -
(b) 1 2 2 2 2
cos [ 2(x y )/(x y )]
-
- - +
(c) 1 2 2 2 2
cos [ (x y ) /(x y )]
-
- + -
(d) 1 2 2 2 2
cos [ (x y )/(x y )]
-
- - +
36. A force of k̂
F
– acts on O, the origin of the coordinate
system. The torque about the point (1, –1) is
X
Y
Z
O
(a) )
j
ˆ
î
(
F - (b) )
ĵ
î
(
F +
-
(c) )
ĵ
î
(
F + (d) )
j
ˆ
î
(
F -
-
37. The component of vector ˆ ˆ
a 2i 3j
= +
r
along the vector
i + j is
(a)
2
5
(b) 2
10
(c) 2
5 (d) 5](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-89-320.jpg)



![89
Motion in a Plane
4. Thecomponent ofa vector ralong X-axiswill havemaximum
value if
(a) r is along positive Y-axis
(b) r is along positive X-axis
(c) r makes an angle of 45° with the X-axis
(d) r is along negative Y-axis
5. The horizontal range of a projectilefired at an angleof 15° is
50 m. Ifit is fired with the same speed at an angle of 45°, its
range will be
(a) 60m (b) 71m
(c) 100m (d) 141m
6. Consider the quantities, pressure, power, energy, impulse,
gravitational potential, electrical charge, temperature, area.
Out of these, the only vector quantities are :
(a) impulse, pressure and area
(b) impulseand area
(c) area and gravitational potential
(d) impulse and pressure
7. In a two dimensional motion, instantaneous speed v0 is a
positive constant. Then, which of the following are
necessarily true?
(a) The average velocity is not zero at any time
(b) Average acceleration must always vanish
(c) Displacements in equal time intervals are equal
(d) Equal path lengths are traversed in equal intervals
8. In a two dimensional motion, instantaneous speed v0 is a
positive constant. Then, which of the following are
necessarily true?
(a) The acceleration ofthe particle is zero
(b) The acceleration of the particle is bounded
(c) The acceleration of the particle is necessarily in the
plane of motion
(d) The particle must be undergoing a uniform circular
motion
NEET/AIPMT (2013-2017) Questions
9. The velocity ofa projectile at the initial pointA is $
( )
2 3
i j
+
$
m/s. It’s velocity (in m/s) at point B is [2013]
(a) $
2 3
i j
- +
$ (b) $
2 3
i j
-
$
(c) $
2 3
i j
+
$ (d) $
2 3
i j
- -
$
10. Vectors ,
A B
r r
and C
r
are such that 0
A B
× =
r r
and 0.
A C
× =
r r
Then the vector parallel to A
r
is [NEET Kar. 2013]
(a) and
B C
r
r
(b) A B
´
r r
(c) B C
+
r
r
(d) B C
´
r
r
11. A particle is moving such that its position coordinate (x, y)
are
(2m,3m) attimet = 0
(6m, 7m) at time t = 2 s and
(13m, 14m) attimet = 5s.
Average velocity vector av
(V )
r
from t = 0 to t = 5s is : [2014]
(a)
1 ˆ ˆ
(13i +14j)
5
(b)
7 ˆ ˆ
(i + j)
3
(c) ˆ ˆ
2(i + j) (d)
11 ˆ ˆ
(i + j)
5
12. A ship A is moving Westwards with a speed of 10 km h–1
and a ship B 100 km South ofA, is moving Northwards with
a speed of 10 km h–1. The time after which the distance
between them becomes shortest, is : [2015]
(a) 5 h (b) 5 2 h
(c) 10 2 h (d) 0 h
13. If vectors ˆ ˆ
A cos ti sin tj
= w + w
r
and
t t
ˆ ˆ
B cos i sin j
2 2
w w
= +
r
are functions of time, then the value of t at which they are
orthogonal to each other is : [2015 RS]
(a) t
2
p
=
w
(b) t
p
=
w
(c) t = 0 (d) t
4
p
=
w
14. The position vector of a particle R
r
as a function of time is
given by:
ˆ ˆ
R 4sin(2 t)i 4cos(2 t)j
= p + p
r
Where R is in meter, t in seconds and î and ĵ denote unit
vectors along x-and y-directions, respectively.
Which one of the following statements is wrong for the
motion of particle? [2015 RS]
(a) Magnitude of acceleration vector is
2
v
R
, where v is
the velocity of particle
(b) Magnitude of thevelocityofparticle is 8 meter/second
(c) path of the particle is a circle ofradius 4 meter.
(d) Acceleration vector is along - R
r
15. A particle moves so that its position vector is given by
ˆ ˆ
r cos tx sin ty
= w + w
r
. Where w is a constant. Which ofthe
following is true ? [2016]
(a) Velocityand acceleration both are perpendicular to r
r
(b) Velocityand acceleration both are parallel to r
r
(c) Velocity is perpendicular to r
r
and acceleration is
directed towards the origin
(d) Velocity is perpendicular to r
r
and acceleration is
directed awayfrom the origin
16. If the magnitude of sum of two vectors is equal to the
magnitude of difference of the two vectors, the angle
between these vectors is : [2016]
(a) 0° (b) 90°
(c) 45° (d) 180°
17. The x and ycoordinates of the particle at anytime are x = 5t
– 2t2 and y = 10t respectively, where x and y are in meters
and t in seconds. The acceleration of the particle at t = 2s is
(a) 5 m/s2 (b) –4 m/s2 [2017]
(c) –8 m/s2 (d) 0](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-93-320.jpg)
![90 PHYSICS
EXERCISE - 1
1. (b) 2.(d)
3. (d) q
=
q
-
q
= 2
2
2
2
2
2
1
tan
g
2
/
)
º
90
(
sin
u
g
2
/
sin
u
H
H
4. (d) 5. (a)
6. (a) In vector addition, the commutative law is obeyed
i.e., A
B
B
A
r
r
r
r
+
=
+
Vector subtraction does not follow commutative law.
7. (d) Since B
.
A
0
C
.
A
r
r
r
r
=
= , itmeans that A
r
isperpendicular
to both B
&
C
r
r
, hence A
r
is parallel to )
C
B
(
r
r
´ or
)
B
C
(
r
r
´ .
8. (a) The unit vector of any vector A
r
is defined as
|
A
|
A
 r
r
=
9. (c) On earth, R = u2 sin 2q/g.
On moon, g' = g/6
R' = u2 sin 2q/g' = 6u2 sin2q/g = 6R.
10. (c)
B
A
2
B
A
R
cos
2
2
2
-
-
=
q 0
B
A
2
R
R 2
2
=
-
=
2
/
p
=
q
11. (c) ]
cos
AB
2
B
A
[
R 2
2
2
q
+
+
=
q
+
+
= cos
R
2
R
R
R 2
2
2
2
2
/
1
cos
or
cos
R
2
R 2
2
-
=
q
q
=
- or 3
/
2p
=
q
12. (c) The dot product should be zero.
13. (c) )
g
/
u
(
2
3
g
º
60
sin
u
R 2
2
º
30 =
=
g
/
u
g
90
sin
u
R 2
2
º
45 =
=
)
2
/
3
(
g
u
g
º
30
cos
u
g
º
120
sin
u
R
2
2
2
º
60 =
=
=
so 30º 60º 45º
R R R
= > or A C B
R R R
= >
14. (a) 2
1
1 mr
F w
= ; 2
2
2 mr
F w
=
since period T is same, so w is same, because
w
p
=
2
T .
Hence ÷
÷
ø
ö
ç
ç
è
æ
=
2
1
2
1
r
r
F
F
15. (a) A parabola
16. (a)
2 2
1
u sin
h
2g
q
=
2 2
2
u sin (90 )
h
2g
-q
= ,
2
u sin 2
R
g
q
=
Range R is same for angle q and (90° – q)
2 2 2 2
1 2
u sin u sin (90 )
h h
2g 2g
q - q
= ´
4 2 2
2
u (sin ) sin (90 )
4g
q ´ -q
= [ sin(90 ) cos ]
- q = q
Q
4 2 2
2
u (sin ) cos
4g
q ´ q
= [ sin 2 2sin cos ]
q = q q
Q
4 2
2
u (sin cos )
4g
q q
=
4 2
2
u (sin 2 )
16g
q
=
2 2 2
2
(u sin 2 ) R
16
16g
q
= =
or, R2 = 16 h1h2 or 1 2
R 4 h h
=
17. (b) Ifthere isnoresistance, bomb will drop ata placeexactly
below the flying aeroplane. But when we take into
account air resistance, bomb will face deceleration in
its velocity. So, it will fall on the earth exactly behind
the aeroplane.
18. (b)
19. (c) From the resultant path of the particle, when it is
projected at angle q with its velocity u is
q
-
q
=
2
2
2
cos
u
gx
2
1
tan
x
y
y
B
D
O
q
A
C
a
n
o
n
Where y denotes the instantaneous height of particle
when it travels an instantaneous horizontal distance x.
herex = D, u = vo
so
2
2 2
0
1 gD
y D tan
2 v cos
= q -
q
20. (d) Max. height =
g
2
)
90
(
sin
v
H
2
2
q
-
= .....(i)
Time of flight,
g
)
90
sin(
v
2
T
q
-
= ...(ii)
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-94-320.jpg)
![91
Motion in a Plane
Horizontal
Vertical
v
q
From (i),
g
H
2
g
cos
v
=
q
,From (ii),
2H 8H
T = 2
g g
=
21. (a) For A: It goes up with velocity u will it reaches its
maximumheight (i.e. velocitybecomeszero) andcomes
back to O and attains velocity u.
Using as
2
u
v 2
2
+
= Þ gh
2
u
v 2
A +
=
O vx
u =
vX
u =
A
v
B
v
C
v
u
u
h
2 2
c x y
v v v
= +
For B, going down with velocity u
Þ gh
2
u
v 2
B +
=
For C, horizontal velocityremains same, i.e. u.Vertical
velocity= gh
2
0 + = gh
2
The resultant C
v = 2
y
2
x v
v + = gh
2
u2
+ .
Hence C
B
A v
v
v =
=
22. (c) Since horizontal component ofthevelocityof thebomb
will be the same as the velocity of the aeroplane,
therefore horizontal displacements remain the same at
anyinstant of time.
23. (a) In uniform circular motion speed is constant. So, no
tangential acceleration.
It hasonlyradial acceleration
R
v
a
2
R = [directedtowards
center]
anditsvelocityisalwaysin tangential direction. Sothese
two areperpendicular toeach other.
24. (d) 2usin ( )
T
gcos
q - a
=
a
25 (d) Velocityand kinetic energyis minimum at the highest
point.
q
= 2
2
cos
v
m
2
1
E
.
K
EXERCISE - 2
1. (b) K.E. isminimum at the highestpoint. So,the horizontal
distanceishalfoftherangeRi.e., 0.5R.
2. (b)
g
30
sin
u
g
2
sin
u
R
2
2
1 =
q
= or 3
g
u
or
g
2
u
5
.
1
2
2
=
=
km
3
g
u
g
90
sin
u
R
2
2
2 =
=
=
3. (b) The bullets are fired at the same initial speed
º
30
sin
º
60
sin
º
30
sin
u
g
2
g
2
º
60
sin
u
H
H
2
2
2
2
2
2
=
´
=
¢
2
2
( 3 / 2) 3
1
(1/ 2)
= =
4. (b)
5. (a) 20
)
k̂
4
j
ˆ
3
).(
k̂
5
î
2
(
F
.
F 2
1 =
+
+
=
r
r
6. (d)
g
2
sin
u
2
g
cos
sin
2
u 2
2
2
q
´
=
q
q
or tan q = 2
7. (a) 2 2
1 3 1
m(u cos ) m u
2 4 2
q = ´
or
4
3
cos 2
=
q or º
30
cos
2
3
cos =
=
q .
8. (c)
9. (d)
g
u
6
or
g
u
R
2
2
=
= ;
q
-
q
= 2
2
2
cos
u
2
x
g
tan
x
y
or ÷
ø
ö
ç
è
æ
-
=
6
1
º
45
cos
2
4
º
45
tan
2
h 2
m
3
4
3
2
2 =
-
=
10. (c) We know that,
g
2
)
sin
u
(
H
y
2
m
q
=
=
g
2
sin
u 2
2
q
=
.
u
u
2
H
H D
=
D
Given %
2
u
u
=
D
H
2 2 4%
H
D
= ´ =
11. (c) As,
2
gt
2
1
t
sin
u
s -
q
=
so 2
t
10
2
1
t
)
2
/
3
(
3
20
40 ´
´
-
´
=
or 5t2 – 30t + 40 = 0 or t2 – 6t + 8 = 0
or t = 2 or 4.
Theminimum timet = 2s.
12. (a) 2
2
5
4
R +
= N
41
=
q
R
5N
4N](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-95-320.jpg)

![93
Motion in a Plane
28. (c) A body is in translational equilibrium when the
components of all external forces cancel.
Forthesheet :Fcos q=4 N, Fsinq =3 N.Themagnitude
of F is found byadding the squares ofthe components:
F2cos2 q+ F2 sin2 q = F2 = 42 + 32 = 25 N2. Therefore F
= 5 N. The F vector points in the proper direction,
since tan q = 0.75 = 3/4.
29. (a)
ˆ ˆ ˆ
i j k
v 1 2 2
0 4 3
= -
-
r
v
r
]
0
4
[
k̂
]
3
0
[
j
ˆ
]
8
6
[
î -
+
+
+
-
=
v
r
k̂
4
j
ˆ
3
î
2 +
+
-
= | v | 29 units
Þ =
uu
r
.
30. (b) Use tan
q
+
q
=
a
cos
P
Q
sin
P
Þ tan 90° ¥
=
q
+
q
=
cos
P
Q
sin
P
Q + P cos q = 0 Þ P cos q = -Q.
R= q
+
+ cos
PQ
2
Q
P 2
2
R = 2
2
2
Q
2
Q
P -
+ or R = 2
2
Q
P - = 12
144 = (P + Q)(P - Q) or P - Q = 144/18 = 8.
P = 13 N and Q = 5 N.
31. (b) | A.B| | A B |
= ´
r r
r r
ABcos ABsin
Þ q = q
1
tanθ =1 cosθ =
2
Þ Þ
Now, 2 2
| A B | A B 2ABcos
+ = + + q
r r
2 2 1
A B 2AB.
2
= + + 2 2
A B 2AB
= + +
32. (b)
ˆ ˆ ˆ
3i bj 2k 3 6 2
ˆ ˆ ˆ
 i j k
7 7 7
9 36 4
+ + + æ ö
= = + +
ç ÷
+ + è ø
. If a, b and g are
angles made by A with coordinate axes, then
7
2
cos
and
7
6
cos
,
7
3
cos =
g
=
b
=
a .
33. (b) Solve two equations : R2 = 9P2 + 4P2 + 12P2 cosq and
4R2 = 36P2 + 4P2 + 24P2 cosq.
34. (b)
35. (a)
2
2 2 2 2
x y (x y) (x y) 2(x y)(x y)cos
æ ö
+ = + + - + + - q
ç ÷
è ø
2 2 2 2 2 2 2 2
x y x y 2xy x y 2xy 2(x y )cos
Þ + = + + + + - + - q
or 2 2 2 2
2(x y ).cos (x y )
- q = - +
2 2
1
2 2
(x y )
cos
2(x y )
-
é ù
- +
Þ q = ê ú
-
ê ú
ë û
36. (c) Torque ˆ ˆ ˆ
r F (i j) ( Fk)
t = ´ = - ´ -
u
r r ur
ˆ ˆ ˆ ˆ
F[ i k j k]
= - ´ + ´ ˆ ˆ ˆ ˆ
F(j i) F(i j)
= + = +
ˆ ˆ ˆ ˆ ˆ ˆ
Since k i j and j k i
é ù
´ = ´ =
ë û
37. (a) Component of a
r
along
a . b
b
| b |
=
r
r
r
r
38. (a) x
u 30cos30º 30 3 /2,
= = , uy = 30 sin 30°,
y
v 30sin30 gt
= °-
0
5
.
1
10
º
30
sin
30
vy =
´
-
=
As vertical velocity = 0,
Angle with horizontal a= 0º
It is a state, when a particle reach to a highest point of
its path.
39. (c) From conservation of linear momentum,
1 2
m m
mv v v
2 2
= +
r r r
q
120 m/s
y
Explode
= 50m/sec
v1
v2
50 m/s
(here we take particle & earth as a system so in this
case external force is zero & linear momentum is
conserved)
Where v
r
is velocity of particle before explosion &
1 2
v ,v
r r
are velocity of its equal pieces.
here ˆ
v 60i
=
r (in x direction),
1
ˆ
v 50j
=
r
(in ydirection)
so 2
ˆ ˆ
v 120i 50 j
= -
r
or 2
| v | 130m/sec
=
r
&
[From conservation of linear momentum]
120
50
tan
-
=
q
40. (b) There is no change in horizontal velocity, hence no
change in momentum in horizontal direction. The
vertical velocity at t = 10sec is
10
)
8
.
9
(
º
60
sin
98
v ´
-
´
= = –13.13 m/sec
sochange in momentum in vertical direction is
= (0.5 98 3/2) [ (0.5 13.13)]
´ ´ - - ´
=42.434+6.56 =48.997»49
41. (b) Maximum possible horizontal range = v2/g
Maximum possible area of the circle
2
2 4
2
v v
g g
æ ö p
= p =
ç ÷
ç ÷
è ø
2
v
Here r
g
é ù
=
ê ú
ê ú
ë û](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-97-320.jpg)


![96 PHYSICS
62. (d) j
ˆ
)
t
sin
a
(
î
)
t
cos
a
(
r w
+
w
=
r
dt
d
dt
)
r
(
d
v =
=
r
}
j
ˆ
)
t
sin
a
(
î
)
t
cos
a
{( w
+
w
ĵ
)
t
cos
a
(
î
)
t
sin
a
( w
w
+
w
w
-
=
]
j
ˆ
)
t
cos
a
(
î
)
t
sin
a
[( w
+
w
-
w
=
r.v 0
=
r r
velocity is perpendicular to the displacement.
63. (b) Since
m
E
2
v
mv
2
1
E 2
=
Þ
=
Now at highest point of flight, the vertical component
of velocity is zero & onlyhorizontal component is non
zero. SoK.E. at highest point is
2
1
E ' m(v cos 45º )
2
=
=E /2
64. (b) Given, u1 = u2 = u, q1 = 60º, q2 = 30º
In Ist case, we know that range
g
)
30
90
sin(
u
g
120
sin
u
g
)
60
(
2
sin
u
R
2
2
2
1
°
+
°
=
°
=
°
=
2 2
u (cos 30 ) 3u
g 2g
°
= =
In IInd case when °
=
q 30
2 , then
g
2
3
u
g
60
sin
u
R
2
2
2 =
°
= Þ R1 = R2
(we get same value of ranges).
65. (a) ˆ ˆ
F = 6ti + 4tj or x y
6t 4t
a ,a
3 3
= =
so 2
t
u = a dt = t
o
x x
ò (u ) = 9m/sec
x t=3
Þ
and
2
2t
t
u = a dt =
y y
o 3
ò sec
/
m
6
)
u
( 3
t
y =
Þ =
(because ux & uy = 0 at t = 0 sec)
66. (b)
2
gt
2
1
s = , s and g are same for both the balls, so time
of fall ‘t’ will also be the same for both of them (s is
vertical height)
67. (c) B
A
sum
vector
P
r
r
r
+
=
=
Q vector differences A B
= = -
r r r
Since P
r
and Q
r
are perpendicular
0
Q
.
P =
r
r
Þ (A B).(A B) 0
+ - =
r r
r r
Þ A
A2 = B2
Þ B
A =
68. (b) Circumferenceofcircleis 2pr = 40m
Total distance travelled in tworevolution is 80m. Initial
velocityu =0, final veloctiyv = 80 m/sec
so from
v2 =u2+2as
Þ (80)2 =02+2×80×a
Þ a = 40m/sec2
69. (b) q
=
´ sin
B
A
|
B
A
|
r
r
q
= cos
B
A
B
.
A
r
r
B
.
A
3
|
B
A
|
r
r
r
r
=
´
Þ AB sin q = Ö3 AB cos q or tan q = Ö3
q = 60º
2 2
| A B| A B 2ABcos60º
+ = + +
r r
AB
B
A 2
2
+
+
=
70. (b) For two vectors to be perpendicular to each other
A B
® ®
× = 0
(2 3 8
i j k
Ù Ù Ù
+ + )· (4 4
j i k
Ù Ù Ù
- +a )= 0
–8 + 12 + 8a = 0 or a = - = -
4
8
1
2
71. (d) 72. (c) 73. (d) 74. (d) 75. (a)
EXERCISE - 3
Exemplar Questions
1. (b) Given, ˆ ˆ
A i j
= +
ˆ ˆ
B i j
= -
As we know that
| || | cos
A B A B
× = q
r r
2 2 2 2
ˆ ˆ ˆ ˆ
( ) ( ) ( 1 1 )( 1 1 )cos
i j i j
+ × - = + + q
( )( ) 2 2 cos
i j i j
+ - = ´ q
where q is the angle between A and B
1 0 0 1
cos 0
2 2
- + -
q = =
q = 90°
2. (d) A scalar quantity does not depend on direction so it
has the same value for observers with different
orientations of the axes.
3. (b) From the diagram, ˆ ˆ
u ai bj
= +
As u is in the first quadrant, so both components a
and b will be positive.
For ˆ ˆ,
v pi qj
= + as it is in positive x-direction and
located downward so x-component p will be positive
and y-component q will be negative.
Hence, a, b and p are positive but q is negative.
4. (b) Let r makes an angle q with positive x-axis component
of r along x-axis.
| | cos
x
r r
= q
maximum maximum
( ) | | (cos )
x
r r
= q
| | cos0 | |
r r
= ° =
( cosq
Q is maximumofq=0°)
q = 0°.
Hence the vector r has maximum value along positive
x-axis.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-100-320.jpg)
![97
Motion in a Plane
5. (c) Consider, projectile is fired at an angle q.
According to question,
q = 15° and R = 50 m
R
X
Y
u
q
Range,
2
sin 2
u
R
g
q
=
2
sin(2 15 )
50m
u
R
g
´ °
= =
2 2 1
50 sin30
2
g u u
´ = ° = ´
50 × g × 2 = u2
2
50 9.8 2 100 9.8 980
u = ´ ´ = ´ =
980
u = = 31.304 m/s 14 5
=
2
( 9.8 m/s )
=
g
Q
Now, 45 ;
q = °
2 2
sin 2 45
u u
R
g g
´ °
= =
2
(14 5) 14 14 5
100 m
9.8
R
g
´ ´
= = =
6. (b) As we know that,
Impulse,
D
æ ö
= D = D = D
ç ÷
è ø
D
p
I F t t p
t
where F is force, Dt is time duration and Dp is change
in momentum.AsDp is a vector quantity, henceimpulse
is also a vector quantity. Sometimes area can also be
treated as vector.
7. (d) As speed is a scalar quantity, hence it will be related
with path length (scalar quantity) only.
Hence, Speed 0
total distance travelled
time taken
v =
So, total distance travelled = Path length
= (speed) × time taken
Hence, path length which is scalar and traversed in
equal intervals.
8. (c) As given that in two dimensional motion the
instanteous speed v0 is positive constant and we know
that acceleration is rate of change of velocity or
instantaneous speed and hence it will also be in the
plane of motion.
NEET/AIPMT (2013-2017) Questions
9. (b) At point B the direction of velocity component of the
projectile along Y - axis reverses.
Hence, B
V
®
= 2i 3j
-
$ $
10. (d) Vector triple product
( ) ( ) ( ) 0
A B C B A C C A B
´ ´ = × - × =
r r r r r r
r r r
Þ || ( )
A B C
´
r r
r
[ 0 and 0]
× = × =
r r r
r
Q A B A C 1.
(a) 2 2
( ) ( )
A B C
+ =
r r
r
2 2
2 .
A B A B C
2
Þ + + =
r r
2 2
3 4 2 . 5
A B
2
Þ + + =
r r
2 . 0
A B
Þ =
r r
or . 0
A B
Þ =
r r
A B
^
r r
Here A2 + B2 = C2. Hence, A B
^
uu
r uu
r
11. (d) av
v
r
=
r (displacement)
t (time taken)
D
D
r
=
ˆ ˆ
(13 2)i (14 3)j
5 0
- + -
-
=
11 ˆ ˆ
(i j)
5
+
12. (a) ( )
A
V 10 –i
=
ur
$
( )
B
V 10 j
=
ur
$
BA
ˆ
V 10 j 10 i 10 2 km / h
= + =
ur
$
DistanceOB = 100 cos 45° = 50 2 km
O
S
100 km
w 10 km/h A
45°
100 km
N(j)
$
BA
V 10 2 km / h
=
B
Time taken to reach the shortest distance between
A and
BA
OB
B
V
= uuuur
50 2
5h
10 2
= =
13. (b) Two vectors are
A
r
= ˆ ˆ
cos ti sin tj
w + w
B
r
=
t t
ˆ ˆ
cos i sin j
2 2
w w
+](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-101-320.jpg)



![101
Lawsof Motion
B
dx
v velocity of block
dt
ù
= = ú
û
Again differentiating we get, 2ap = aB
B
p B
dv
dVp
a and a
dt dt
é ù
= =
ê ú
ë û
ap = acceleration of pulley, aB = acceleration of block
Case 2 Here =
+
+ y
x
h 2
2
constt. On differentiating w.r.t ‘t’
F
x
y
h
q
1 2
[Negative sign with dy/dt shows that with increase in time, y
decreases]
2 2
1 2x dx dy
0
dt dt
2 h x
´
- =
+
Þ cos q (v1 – v2) = 0
2 2
x
cos
h x
é ù
q =
ê ú
ê ú
+
ë û
Q
Case 3 Wedge block system : Thin lines represents thecondition
of wedge block at t = 0 and dotted lines at t = t
ax
c
Ax
Ax A
q
q
B
ay
ax
ay
Ax = acceleration of wedge towards left
ax, ay = acceleration of block as shown
From DABC, y
x x
a
tan
a A
q =
+
Frame of Reference :
Reference frames are co-ordinate systems in which an event is
described.
There are two typesof reference frames
(a) Inertial frame of reference: These are frames of reference
in which Newton’s laws hold good. These frames are at rest
with each other or which are moving with uniform speed
with respect to each other.
All reference frames present on surface of Earth are
supposed to be inertial frame of reference.
(b) Non – inertial frame of reference: Newton’s law do not
hold good in non-inertial reference frame.
All accelerated and rotatory reference frames are non –
inertial frameof reference. Earth isa non-intertial frame.
When the observer is in non-inertial reference framea
pseudo force is applied on the body under observation.
Free Body Diagram (FBD) :
Free body diagram of a mass is a separate diagram of that mass.
All forces acting on the mass are sketched. A FBD is drawn to
visualise the direct forces acting on a body.
Case 1 : Masses M1 and M2 are tied to a string, which goes over
a frictionless pulley
(a) If M2 > M1 and they move with accelerationa
1
M
M2
M g
2
M g
1
T
T
a
a
FBD of M1, FBD of M2
T
M1
1
M g
a
T
M2
M g
2
a
1 1
T M g M a
- = 2 2
M g T M a
- =
where T is the tension in the string. It gives
2 1
1 2
M M
a g
M M
-
=
+
and 1 2
1 2
2M M
T g
M M
=
+
(b) If the pulley begins to move with acceleration f,
downwards
2 1
1 2
( )
M M
a g f
M M
-
= -
+
uu
r uu
r uu
r
and 1 2
1 2
2
( )
M M
T g f
M M
= -
+
ur uu
r uu
r
Case 2 : Three massesM1, M2 and M3 are connected with strings
as shown in the figure and lie on a frictionless surface. They are
pulled with a force F attached to M1.
M3 M2 M1 F
T 1
T1
T2
T2
The forces on M2 and M3 are as follows
2 3
1
1 2 3
M M
T F
M M M
+
=
+ +
and 3
2
1 2 3
M
T F
M M M
=
+ +
;
Acceleration of the system is
1 2 3
F
a
M M M
=
+ +
Case 3 : Two blocks of masses M1 and M2 are suspended
vertically from a rigid support with the help of strings as shown
in the figure. The mass M2 is pulled down with a force F.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-105-320.jpg)

![103
Lawsof Motion
FBD of M2 a
T
M g
2
M gcos
2 b
M
gsin
2
b
M
2
b
Equation of motion for M2
M2g sinb – T = M2a
or T = M2g sin b – M2a ...(2)
Using eqn. (1) and (2) we get,
M1g sin a + M1a = M2g sin b – M2a
Solving we get,
( )
2 1
1 2
sin sin
M M g
a
M M
b - a
=
+
and 1 2
1 2
[sin sin ]
M M g
T
M M
= b + a
+
Case 7 :Aperson/monkey climbing a rope
T
Mg
a
a
(a) A person of mass M climbs up a rope with acceleration a.
The tension in the rope will be M(g+a).
T – Mg = Ma Þ T = M(g + a)
(b) If the person climbs down along the rope with acceleration
a, thetension in the rope will be M(g–a).
a a
Mg
T
Mg – T = Ma Þ T = M(g – a)
(c) When the person climbs up or down with uniform speed,
tension in the string will be Mg.
Case 8 : Abodystarting from rest moves along a smooth inclined
plane of length l, height h and having angle of inclination q.
h
l
q
FBD of body
N=R
mg
mg sinq mg cosq
q
(where N=R is normal reaction applied by plane on the body
of mass m)
For downward motion, along the inclined plane,
q
=
Þ
=
q sin
g
a
ma
sin
mg
Bywork-energytheorem loss in P.E. = gain in K.E.
gh
2
v
mv
2
1
mgh 2
=
Þ
=
Þ
Also, from the figure, h = l sin q. q
=
=
sin
g
2
gh
2
v l
(a) Acceleration down the plane is g sin q.
(b) Its velocity at the bottom of the inclined plane will be
2 2 sin
gh g
= q
l
(c) Time taken to reach the bottom will be
1/ 2
1/ 2
2 1/ 2
2 2 1 1 2
sin sin
sin
sin
2
h h
t
g g
g g
h
æ ö
æ ö
= = = =
ç ÷
ç ÷ ç ÷
q q
q
è ø æ ö
è ø qç ÷
è ø
l
(d) Ifangles ofinclination are q1 and q2 for twoinclined planes
Keeping the length constant then
½
1 2
2 1
sin
sin
t
t
æ ö
q
= ç ÷
q
è ø
Case 9 : Weight of a man in a lift :
(i) When lift is acceleratedupward :In thiscase theman also
movesin upwarddirection with an acceleration a
r
.
N
a a
mg
Then from Newton’ second law
N – mg = ma or N = m(g + a)
or Wapp = m(g + a) (1 / )
o
W a g
= + (as W = mg)
Where Wapp is apparent weight ofthe man in the lift, Wo is
thereal weight, N isthe reaction oflift on theman. It is clear
that N = Wapp
When the lift moves upward and if we measure the weight
of the man byany means (such as spring balance) then we
observe more weight (i.e., Wapp) than the real weight (Wo)
Wapp >Wo
(ii) When lift is accelerated downward : In this case from
Newton’s second law
N
a
mg
mg – N = ma
or N = m(g – a) = Wo(1– a/g)
or W'app= Wo(1– a/g) { }
mg
Wo =
Q
If we measure the weight of man by spring balance, we
observe deficiency because Wapp< Wo.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-107-320.jpg)
![104 PHYSICS
(iii) Whenlift is at rest or movingwithconstantvelocity :From
Newton’s second law N –mg = 0 or N = mg
In this case spring balance gives the true weight of the man.
Case 10 : Three masses M1, M2 and M3 are placed on a smooth
surface in contact with each other as shown in the figure.
A force F pushes them as shown in the figure and the three
masses move with acceleration a,
M3
M2
F2
F1
F2 F1
M1
F
a
M1
F
F1
Þ F – F1 = m1a ...(i)
M2
F2
F1
Þ F1 – F2 = m2a ...(ii)
F2
M3
Þ F2 = M3 a ...(iii)
Adding eqns. (i), (ii) and (iii) we get,
1 2 3
F
a
M M M
=
+ +
Þ 3
2
1 2 3
M F
F
M M M
=
+ +
and 2 3
1
1 2 3
( )
M M F
F
M M M
+
=
+ +
Keep in Memory
1. When a man jumps with load on his head, the apparent
weight of the load and the man is zero.
2. (i) If a person sitting in a train moving with uniform
velocitythrows a coin verticallyup, then coin will fall
back in his hand.
(ii) If the train is uniformlyaccelerated, the coin will fall
behind him.
(iii) Ifthe train is retarded uniformly, then the coin will fall
in front ofhim.
Example1.
A chain of length l is placed on a smooth spherical surface
of radius R with one of its ends fixed at the top of the
sphere. What will be the acceleration a of each element of
the chain when its upper end is released? It is assumed
that the length of chain
R
π
2
æ ö
<ç ÷
è ø
l .
Solution :
Let m be the mass of the chain of length l. Consider an
element of length dlof thechain at an angle q with vertical,
R
q
dl
dq
From figure, dl = R d q ;
Mass of the element,
dm = l
l
d
m
; or dm = q
d
R
.
m
l
Force responsible for acceleration, dF = (dm)g sinq ;
dF = q
q
=
q
÷
ø
ö
ç
è
æ
q d
sin
mgR
)
sin
g
(
d
R
m
l
l
Net force on the chain can be obtained by integrating the
above relation between 0 to a, we have
ò
a a
a
-
=
q
-
=
q
q
=
0 0
]
cos
1
[
R
mg
)
cos
(
R
mg
d
sin
R
mg
F
l
l
l
ú
û
ù
ê
ë
é
-
=
R
cos
1
R
mg l
l
;
Acceleration,
F gR
a 1 cos
m R
æ ö
= = -
ç ÷
è ø
l
l
.
Example2.
A block slides down a smooth inclined plane to the ground
when released at the top, in time t second. Another block
is dropped vertically from the same point, in the absence
of the inclined plane and reaches the ground in t/2 second.
Then find the angle of inclination of the plane with the
vertical.
Solution :
If q is the angle which the inclined plane makes with the
vertical direction, then the acceleration of the block sliding
down the plane of length l will be g cosq.
A
C B
q
l h
Using the formula, 2
at
2
1
ut
s +
= , we have s = l, u = 0, t = t
and a = g cos q.
so 2
2
t
)
cos
g
(
2
1
t
cos
g
2
1
t
0 q
=
q
+
´
=
l ...(i)
Taking vertical downward motion of the block, we get
4
/
gt
2
1
)
2
/
t
(
g
2
1
0
h 2
2
=
+
= ...(ii)
Dividing eqn. (ii) by (i), we get
q
=
cos
4
1
h
l
]
/
h
cos
[ l
Q =
q
or
q
=
q
cos
4
1
cos ; or
4
1
cos2
=
q ; or
2
1
cos =
q
or q = 60º](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-108-320.jpg)
![105
Lawsof Motion
Example3.
A large mass M and a small mass
m hang at the two ends of a string
that passes through a smooth
tube as shown in fig. The mass m
moves around a circular path in
a horizontal plane. The length of
the string from mass m to the top
of the tube is l, and q is the angle
the string makes with the
vertical. What should be the
frequency (n) of rotation of mass
m so that mass
M remains stationary? M
m
l
r
q
T
Solution :
Tension in the string T = Mg.
Centripetal force on the body= mrw2 =mr ( 2pn )2. This is
provided by the component of tension acting horizontally
i.e. T sinq ( = Mg sinq).
mr ( 2pn)2 = Mg sinq = Mgr/l. or
1 Mg
2 m
n =
p l
Example4.
A string of negligible mass going over a clamped pulley of
mass m supports a block of mass M as shown in fig. The
force on the pulley by the clamp is given by
(a) 2 Mg
(b) 2 mg
M
m
(c) 2 2
[ (M m) m ]
+ + g
(d) 2 2
[ (M m) M ]
+ + g
Solution : (c)
Force on the pulley by the clamp = resultant of
T = (M + m)g and mg acting along horizontal and vertical
respectively
F 2 2
[(M m)g] (mg)
= + + 2 2
[ (M m) m ]g
= + +
Example5.
The masses of 10 kg and 20 kg respectively are connected
by a massless spring infig. A force of 200 newton actson the
20 kg mass. At the instant shown, the 10 kg mass has
acceleration 12 m/sec2. What is the acceleration of 20 kg
mass?
10 kg
20 kg
200 newton
Solution :
Force on 10 kg mass = 10 × 12 = 120 N
Themassof10kgwill pullthemassof20kgin thebackward
direction with a force of 120 N.
Net force on mass 20 kg = 200 – 120 = 80 N
Its acceleration
force
a
mass
= 2
s
/
m
4
kg
20
N
80
=
=
Example6.
Two masses each equal to m are lying on X-axis at (–a, 0)
and (+ a, 0) respectively as shownin fig. They are connected
by a light string. A force F is applied at the origin and along
the Y-axis. As a result, the masses move towards each other.
What is the acceleration of each mass? Assume the
instantaneous position of the masses as (– x, 0) and (x, 0)
respectively
m O m
(–a, 0) (a, 0)
–X X
F
Solution :
O
(–x, 0) (x, 0)
F
T T
q
B C
A
From figure F = 2 T cos q or T = F/(2 cos q)
The force responsible for motion of masses on X-axis is T
sin q
q
´
q
=
q
=
sin
cos
2
F
sin
T
a
m
)
x
a
(
x
2
F
OA
OB
2
F
tan
2
F
2
2
-
´
=
´
=
q
=
so,
)
x
a
(
x
m
2
F
a
2
2
-
´
=
Example7.
A block of mass M is pulled along horizontal frictionless
surface by a rope of mass m. Force P is applied at one end
of rope. Find the force which the rope exerts on the block.
Solution :
The situation is shown in fig
M
T O
m
P
Let a be the common acceleration of the system. Here
T = M a for block
P – T = m a for rope
P – M a = m a or P = a (M + m) or
)
m
M
(
P
a
+
=
)
m
M
(
P
M
T
+
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-109-320.jpg)

![107
Lawsof Motion
Example10.
A hammer of mass M strikes a nail of mass m with velocity
of u m/s and drives it ‘s’ meters in to fixed block of wood.
Find the average resistance of wood to the penetration of
nail.
Solution :
Applying the law of conservation of momentum,
m u = (M + m) v0 Þ u
M
m
M
v0 ÷
ø
ö
ç
è
æ
+
=
There acceleration a can be obtained using the formula
(v2 = u2 + 2as).
Here we have 0 – v0
2 = 2as or a = v0
2 /2s
s
2
u
M
m
M
a
2
2
÷
ø
ö
ç
è
æ
+
=
Resistance = (M + m) a
2 2
M u
m M 2 s
æ ö
= ç ÷
ç ÷
+
è ø
Example11.
A ball of mass 0.5 kg is thrown towards a wall so that it
strikes the wall normallywith a speed of 10 ms–1. If the ball
bounces at right angles away from the wall with a speed of
8ms–1, what impulse does the wall exert on the ball ?
Solution :
f
10
8
Approaching wall
u = –10 ms–1
Leaving wall
v = +8 ms–1
Taking the direction of the impulse J as positive and using
J = mv – mu
we have
1 1
J 8 ( 10) 9
2 2
= ´ - - = N-s
Therefore the wall exerts an impulse of9 N-s on the ball.
Example12.
Two particles, each of mass m, collide head on when their
speeds are 2u and u. If they stick together on impact, find
their combined speed in terms of u.
Solution :
2u
Before impact
After impact
m
u
v
2m
m
Using conservation of linear momentum (in the direction of
the velocity 2u) we have
(m) (2u) – mu = 2m × V Þ
1
V u
2
=
The combined mass will travel at speed u/2.
(Note that the momentumofthe second particlebefore impact
is negative because its sense is opposite to that specified
as positive.)
Force vary with time and impulse is area under force versus
time curve
Area=Fext.Dt
t
tf
ti
Fext.
Fav
Fext.
(b)
.
Force constant with time i.e., .
ext
F
r
constant with time (shown
by horizontal line) and it would give same impulse to particle
in time Dt = tf – ti as time varying force described.
It is a vector quantityhaving a magnitude equal to the area under
theforce-timecurve asshown in fig. (a). In thisfigure, it isassumed
that force varieswith time and is non-zeroin time interval Dt = tf–
ti. Fig.(b) shows the time averaged force .
ext
F
r
i.e., it is constant
in time interval Dt, then equation (iii) can be written as
f
i
t
ext. t
I F dt
= ò
r
)
t
t
(
F i
f
.
ext -
=
r
t
F
I .
ext D
=
r
...(iv)
The direction of impulsive vector I is same as the direction of
change in momentum. Impulse I has same dimensions as that of
momentum i.e, [MLT–1]
Rocket propulsion (A case of system of variable mass ) : It is
based on principleofconservation of linearmomentum.
In rocket, the fuel burns and produces gases at high temperature.
These gases are ejected out of the rocket from nozzle at the
backside of rocket and the ejecting gas exerts a forward force on
the rocket which accelerates it.
Let the gas ejects at a rate
dt
dM
r -
= and at constant velocity u
w.r.t. rocket then from the conservation of linear momentum
rt
M
ru
M
ru
dt
dv
0 -
=
= whereM = M0 - rt and M0 is mass of rocket
with fuel and solving this equation, we get ÷
÷
ø
ö
ç
ç
è
æ
-
=
rt
M
M
log
u
v
0
0
e
where v = velocity of rocket w.r.t. ground.
Example9.
Two skaters A and B approach each other at right angles.
Skater A has a mass 30 kg and velocity 1 m/s and skater
B has a mass 20 kg and velocity 2 m/s. They meet and
cling together. Find the final velocity of the couple.
Solution :
Applying principle of conservation of linear momentum,
2
2
2
2
1
1
2
1
2
2
2
1 )
v
m
(
)
v
m
(
v
)
m
m
(
;
p
p
p +
=
+
+
=
( ) ( ) ( )
2 2
30 20 v 30 1 20 2 50
+ = ´ + ´ =
50
v 1 m / s
50
= =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-111-320.jpg)


![110 PHYSICS
Solution :
The situation is shown in fig.
F sinq
F cosq
W cosq
W sinq
F
R
q
W
q
q
f= R
m
Let F be the horizontal force needed to just push the object
up the plane. From figure R = W cos q + F sin q
Now f = mR = m [W cos q + F sin q] ...(1)
Further, F cos q = W sin q + f ...(2)
F cos q = W sin q + m [W cos q + F sin q]
F cos q – m F sin q = W sin q + m W cos q
)
sin
(cos
)
cos
(sin
W
F
q
m
-
q
q
m
+
q
=
CASES OF CIRCULAR MOTIONS
Motion in a Vertical Circle :
Let us consider a particle of mass m attached toa string oflength
R let the particle be rotated about its centre O.
At t = 0 the particle start with velocity u from the point A(lowest
point of vertical circle) and at time t its position is P. Then the
tension at point P is given by
T
P
vP
q
q
O
B
R
A u
mg mg
mg cos q
sin q
R
mv
cos
mg
T
2
P
P =
q
- or
R
mv
cos
mg
T
2
P
P +
q
= ...(1)
So tension at point A(lowest point of vertical circle) is
R
mv
mg
T
2
A
A =
- (Q q = 0º) ...(2)
and tension at point B (highest point of vertical circle) is
R
mv
mg
T
2
B
B =
+ (Q q=180º) ...(3)
Where
2
mv
r
is centripetal force required for the particletomove
in a vertical circle.
Now from law of conservation of energy
mgR
2
mv
2
1
mv
2
1 2
B
2
A =
-
or, 2 2
A B
v v 4gR
- = ...(4)
(change in kinetic energyof particle)
= (change in potential energy of particle)
or
(loss in kinetic energyofthe particle) = (gain in potential energy)
In conservative force system (such as gravity force) the
mechanical energy(i.e., kinetic energy+ potential energy) must
be constant.
Total energy will be constant
Nowfrom eqns.(2) and (3), we get
mg
R
TB
vB B
A
D
mg
R
TA
v = v
A C
B
A
D
)
V
V
(
R
m
mg
2
T
T 2
B
2
A
B
A -
+
=
- )
gR
4
(
R
m
mg
2 +
=
Þ mg
6
T
T B
A =
- ...(5)
or TA =TB + 6mg ...(6)
So it is clear from eqn. (6) that tension in string at lowest point
of vertical circle is greater then the tension at highest point of
vertical circle by 6mg.
Condition to complete a vertical circle :
Ifwe reducethevelocityvA in equation (2), then TA will be reduce
and at some critical velocity vc, TB will be zero, then put TB = 0
and vB = vC in equation (3) and we obtain
C B
v v gR
= = ...(7)
In this condition the necessary centripetal force at point B is
provided by the weight of the particle [see again equation (3)]
then from equation (4), we get
2
4 5
A A
v gR gR v gR
- = Þ = ...(8)
then the tension at the point A will be
mg
6
R
)
gR
5
(
m
mg
TA =
+
= ...(9)
Hence if we rotate a particle in a vertical circle and tension in
string at highest point is zero, then the tension at lowest point of
vertical circle is 6 times of the weight of the particle.
Some Facts of Vertical Motion :
(i) The body will complete the vertical circle if its velocity at
lowest point is equal to or greater then gR
5
(ii) The bodywill oscillate about the lowest point if itsvelocity
at lowest point is less then gR
2 . This will happen when
the velocity at the halfwaymark, i.e.
ú
û
ù
ê
ë
é
=
= mgR
mv
2
1
0
v 2
A
D Q
(iii) The string become slack and fails to describe the circle
when its velocity at lowest point lies between
gR
5
to
gR
2](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-114-320.jpg)




![116 PHYSICS
13. A particle ofmass mmoving eastwardwith a speed vcollides
with another particle of the same mass moving northward
with the same speed v. The two particles coalesce on
collision. The newparticleofmass 2mwill movein thenorth-
external direction with a velocity:
(a) v/2 (b) 2v
(c) 2
/
v (d) None of these
14. A spring is compressed between two toy carts of mass m1
and m2. When the toy carts are released, the springs exert
equal and opposite average forces for the same time on
each toy cart. If v1 and v2 are the velocities of the toy carts
and there is no friction between the toy carts and the ground,
then :
(a) v1/v2 = m1/m2 (b) v1/v2 = m2/m1
(c) v1/v2 = –m2/m1 (d) v1/v2 = –m1/m2
15. Two mass m and 2m are attached with each other by a rope
passing over a frictionless and massless pulley. If the pulley
is accelerated upwards with an acceleration ‘a’, what is the
value of T?
(a)
3
a
g +
(b)
3
a
g -
(c)
3
)
a
g
(
m
4 +
(d)
3
)
a
g
(
m -
16. A rider on a horse back falls forward when the horse
suddenly stops. This is due to
(a) inertia of horse
(b) inertia of rider
(c) large weight of the horse
(d) losing of the balance
17. A ball of mass m is thrown verticallyupwards. What is the
rate at which the momentum of the ball changes?
(a) Zero (b) mg
(c) Infinity (d) Data is not sufficient.
18. A small block is shot into each of the four tracks as shown
below. Each of the tracks rises to the same height. The
speed with which the block enters the track is thesame in all
cases.At the highest point of the track, the normal reaction
ismaximumin
(a)
v
(b)
v
(c)
v
(d) v
19. A weight W rests on a rough horizontal plane. If the angle
of friction be q , the least force that will move the body
along the plane will be
(a) q
cos
W (b) q
cot
W
(c) q
tan
W (d) q
sin
W
20. A particle starts sliding down a frictionless inclined plane.
If n
S is the distance traveled byit from time t = n – 1 sec to
t = n sec, the ratio Sn/Sn+1 is
(a)
1
n
2
1
n
2
+
-
(b)
n
2
1
n
2 +
(c)
1
n
2
n
2
+
(d)
1
n
2
1
n
2
-
+
21. Ablock iskepton a inclinedplaneofinclination qoflength l .
The velocity of particle at the bottom of inclined is (the
coefficient offriction is m )
(a) 2
/
1
)]
sin
cos
(
g
2
[ q
-
q
m
l (b) )
cos
(sin
g
2 q
m
-
q
l
(c) )
cos
(sin
g
2 q
m
+
q
l (d) )
sin
(cos
g
2 q
m
+
q
l
22. A bird is in a wire cage which is hanging from a spring
balance . In the first case, the bird sits in the cage and in the
second case, thebird fliesabout insidethecage. Thereading
in the spring balance is
(a) more in the first case
(b) less in first case
(c) unchanged
(d) zero in second case.
23. In an explosion, a bodybreaks up into twopieces ofunequal
masses. In this
(a) both parts will have numerically equal momentum
(b) lighter part will have more momentum
(c) heavier part will have more momentum
(d) both parts will have equal kinetic energy
24. A block of mass m on a rough horizontal surface is acted
upon by two forces as shown in figure. For equilibrium of
block the coefficient offriction between block and surface is
m
q
F1
F2
(a)
q
+
q
+
cos
F
mg
sin
F
F
2
2
1
(b) q
-
+
q
sin
F
mg
F
cos
F
2
2
1
(c)
q
+
q
+
sin
F
mg
cos
F
F
2
2
1
(d)
1 2
2
F sin F
mg F cos
q -
- q
25. A plate of mass M is placed on a horizontal of frictionless
surface (see figure), and a body of mass m is placed on this
plate. The coefficient of dynamic friction between this body
and the plate is m . If a force 2 m mg is applied to the body
ofmass m along the horizontal, theacceleration of the plate
will be
M
m
2 mg
m
(a) g
M
m
m
(b) g
)
m
M
(
m
+
m
(c) g
M
m
2m
(d) g
)
m
M
(
m
2
+
m
.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-120-320.jpg)


![119
Lawsof Motion
26. Two trolleys of mass m and 3m are connected by a spring.
They were compressed and released at once, they move off
in opposite direction and come to rest after covering a
distance S1, S2 respectively. Assuming the coefficient of
friction to be uniform, ratio of distances S1 : S2 is :
(a) 1: 9 (b) 1: 3
(c) 3: 1 (d) 9: 1
27. A particle of mass 10 kg is moving in a straight line. If its
displacement, x with time t is given by x = (t3 – 2t – 10) m,
then the force acting on it at the end of 4 seconds is
(a) 24N (b) 240N
(c) 300N (d) 1200N
28. When forces F1, F2, F3 are acting on a particle of mass m
such that F2 and F3 are mutually perpendicular, then the
particle remains stationary. If the force F1 is now removed
then the acceleration of the particle is
(a) F1/m (b) F2F3/mF1
(c) (F2 – F3)/m (d) F2/m
29. One end of massless rope, which passes over a massless
and frictionless pulley P is tied to a hook C while the
other end is free. Maximum tension that the rope can
bear is 360 N. With what value of maximum safe
acceleration (in ms–2) can a man of 60 kg moves
downwards on the rope? [Take g = 10 ms–2]
P
C
(a) 16 (b) 6
(c) 4 (d) 8
30. A force k̂
10
ĵ
6
î
8
F -
-
=
r
newton produces an acceleration
of 1 ms–2 in a body. The mass of the body is
(a) 10kg (b) 2
10 kg
(c) 3
10 kg (d) 200kg
31. A uniform chain of length 2 m is kept on a table such that a
length of 60 cm hangs freelyfrom the edge of the table. The
total mass of the chain is 4 kg. What is the work done in
pulling the entire chain on the table ?
(a) 12J (b) 3.6J
(c) 7.2J (d) 1200J
32. A body of mass 1 kg moving with a uniform velocity of
1
ms
1 -
. If the value of g is 2
ms
5 -
, then the force acting on
the frictionless horizontal surface on which the body is
moving is
(a) 5N (b) 1N
(c) 0N (d) 10N
33. A trailer of mass 1000 kg is towed by means of a rope
attached to a car moving at a steady speed along a level
road. The tension in the rope is 400 N. The car starts to
accelerate steadily. Ifthe tension in the rope is now 1650 N,
with what acceleration is the trailer moving ?
(a) 1.75ms–2 (b) 0.75ms–2
(c) 2.5 ms–2 (d) 1.25ms–2
34. Arocket of mass5000 kg is to beprojected verticallyupward.
The gases are exhausted verticallydownwards with velocity
1000 ms–2 with respect tothe rocket. What is the minimum
rate of burning the fuel so as to just lift the rocket upwards
against gravitational attraction ?
(a) 49 kg s–1 (b) 147 kg s–1
(c) 98 kg s–1 (d) 196 kg s–1
35. BlocksAand Bof masses 15 kg and 10 kg, respectively, are
connected bya light cable passing over a frictionless pulley
as shown below. Approximately what is the acceleration
experienced by the system?
(a) 2.0m/s2
(b) 3.3m/s2
(c) 4.9m/s2
A
B
(d) 9.8m/s2
36. A50 kg ice skater, initiallyat rest, throwsa 0.15 kg snowball
with a speed of35 m/s. What is the approximate recoil speed
of the skater?
(a) 0.10m/s (b) 0.20m/s
(c) 0.70m/s (d) 1.4m/s
37. Block A is moving with acceleration A along a frictionless
horizontal surface. When a second block, B is placed on top
of Block Athe acceleration of the combined blocks drops to
1/5 the original value. What is the ratio of the mass ofA to
the mass of B?
(a) 5: 1 (b) 1: 4
(c) 3: 1 (d) 2: 1
38. A force F is used to raise a 4-kg mass M from the ground to
a height of 5 m.
60°
F
M
What is the work done bythe force F? (Note : sin 60° = 0.87;
cos60° = 0.50. Ignore friction andthe weightsofthe pulleys)
(a) 50J (b) 100J
(c) 174J (d) 200J
39. A 5000 kg rocket is set for vertical firing. The exhaust speed
is 800 m/s. Togive an initial upward acceleration of 20 m/s2,
the amount of gas ejected per second to supply the needed
thrust will be (Takeg = 10 m/s2)
(a) 127.5kg/s (b) 137.5kg/s
(c) 155.5kg/s (d) 187.5kg/s](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-123-320.jpg)
![120 PHYSICS
40. A bullet is fired from a gun. The force on the bullet is given
byF = 600 – 2 × 105 t
Where, F is in newtons and t in seconds. The force on the
bullet becomes zero as soon as it leaves the barrel. What is
the average impulse imparted to the bullet?
(a) 1.8 N-s (b) Zero
(c) 9 N-s (d) 0.9 N-s
41. A rifle man, whotogether with his rifle has a mass of100 kg,
stands on a smooth surface and fires 10 shots horizontally.
Each bullet hasa mass10 gand a muzzlevelocityof 800 ms–
1. The velocity which the rifle man attains after firing 10
shots is
(a) 8 1
ms-
(b) 0.8
1
ms-
(c) 0.08 1
ms-
(d) – 0.8 1
ms-
42. A block of mass 4 kg rests on an inclined plane. The
inclination to the plane is gradually increased. It is found
that when the inclination is 3 in 5, the block just begins to
slidedown the plane. The coefficient of friction between the
block and the plane is
(a) 0.4 (b) 0.6
(c) 0.8 (d) 0.75.
43. The minimum velocity(in ms-1)with which a car driver must
traverse a flat curveofradius 150m and coefficient offriction
0.6 to avoid skidding is
(a) 60 (b) 30
(c) 15 (d) 25
44. A body of mass 2 kg is placed on a horizontal surface
having kinetic friction 0.4 and static friction 0.5. If the force
applied on the bodyis 2.5 N, then the frictional force acting
on the body will be [g = 10 ms–2]
(a) 8N (b) 10 N
(c) 20N (d) 2.5N
45. Abag ofsand of mass m is suspended bya rope. A bullet of
mass
20
m
is fired at it with a velocity v and gets embedded
into it. The velocity of the bag finally is
(a)
v
21
20
´ (b)
20v
21
(c)
v
20
(d)
v
21
46. For thearrangement shown in the Figure thetension in the
string is [Given : 1
tan (0.8) 39
-
= ° ]
39°
m = 1 kg
m = 0.8
(a) 6N (b) 6.4N
(c) 0.4N (d) zero.
47. A1kg block anda 0.5 kgblock movetogether on a horizontal
frictionless surface . Each block exerts a force of6 N on the
other. The block move with a uniform acceleration of
a
1 kg 0.5 kg
F
(a) 3 2
ms-
(b) 6 2
ms-
(c) 9 2
ms-
(d) 12 2
ms-
48. A body of mass 32 kg is suspended by a spring balance
from the roof of a vertically operating lift and going
downward from rest. At the instant the lift has covered 20 m
and 50 m, the spring balance showed 30 kg and 36 kg
respectively. Then the velocity of the lift is
(a) decreasing at 20 m, and increasing at 50 m
(b) increasing at 20m and decreasing at 50 m
(c) continuously decreasing at a steady rate throughout
the journey
(d) constantly increasing at constant rate throughout the
journey.
49. An object at rest in space suddenly explodes into three
parts of same mass. The momentum of the two parts are
î
p
2 and ĵ
p . The momentum of the third part
(a) will have a magnitude 3
p
(b) will have a magnitude 5
p
(c) will have a magnitude p
(d) will have a magnitude 2p.
50. A triangular block of mass M with angles 30°, 60°, and 90°
rests with its 30°–90° side on a horizontal table. A cubical
block of mass m rests on the 60°–30° side. The acceleration
which M must have relative to the table to keep m stationary
relativeto the triangularblock assuming frictionless contactis
(a) g (b)
2
g
(c)
3
g (d)
5
g
51. Abodyofmass 1.0 kg is falling with an acceleration of 10 m/
sec2. Its apparent weight will be (g = 10 m/sec2)
(a) 1.0 kg wt (b) 2.0 kg wt
(c) 0.5 kg wt (d) zero
52. In the figure a smooth pulley of negligible weight is
suspended by a spring balance. Weight of 1 kg f and
5 kg f are attached to the opposite ends of a string passing
over the pulley and move with acceleration because of
gravity, During their motion, the spring balance reads a
weight of
(a) 6 kg f
(b) less then 6 kg f
(c) more than 6 kg f
1 kg
5 kg
(d) may be more or less then 6 kg f](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-124-320.jpg)


![123
Lawsof Motion
76. A smooth block is released at rest on a 45° incline and then
slides a distance ‘d’. The time taken to slide is ‘n’ times as
much to slide on rough incline than on a smooth incline.
The coefficient of friction is
(a) k
m = 2
n
1
1- (b) k
m =
2
n
1
1-
(c) s
m =
2
n
1
1- (d) s
m =
2
n
1
1-
77. The upper half of an inclined plane with inclination f is
perfectly smooth while the lower half is rough. A body
starting from rest at the top will again come to rest at the
bottom if the coefficient of friction for the lower half is given
by
(a) 2 cos f (b) 2 sin f
(c) tan f (d) 2 tan f
78. A particle of mass 0.3 kg subject to a force F = – kx with k =
15 N/m . What will be its initial acceleration ifit is released
from a point 20 cm awayfrom the origin ?
(a) 15 m/s2 (b) 3 m/s2
(c) 10 m/s2 (d) 5 m/s2
79. A block is kept on a frictionless inclined surface with angle
ofinclination ‘a ’ . The incline isgiven an acceleration ‘a’ to
keep the block stationary. Then a is equal to
a
(a) g cosec a (b) g / tan a
(c) g tan a (d) g
80. Consider a car moving on a straight road with a speed of100
m/s . The distance at which car can be stopped is [µk = 0.5]
(a) 1000 m (b) 800 m
(c) 400 m (d) 100 m
81. A round uniform bodyof radius R, mass M and moment of
inertia I rolls down (without slipping) an inclined plane
making an angle qwith the horizontal. Then its acceleration
is
(a)
2
gsin
1 MR / I
q
,
(b)
2
gsin
1 I / MR
q
∗
(c)
2
gsin
1 MR / I
q
∗
(d)
2
gsin
1 I/ MR
q
,
82. A block of mass m is placed on a smooth wedge of
inclination q. The whole system is accelerated horizontally
so that the block does not slip on the wedge. The force
exerted by the wedge on the block (g is acceleration due to
gravity) will be
(a) mg/cos q (b) mg cos q
(c) mg sin q (d) mg
83. The coefficient of static friction, ms, between block A of
mass 2 kg and the table as shown in the figure is 0.2. What
would be the maximum mass value of block B so that the
two blocks do not move? The string and the pulley are
assumed to be smooth and massless. (g = 10 m/s2)
A
B
2 kg
(a) 0.4kg (b) 2.0kg
(c) 4.0kg (d) 0.2kg
84. A body under the action of a force
ˆ ˆ ˆ
F = 6 i –8 j+10k,
r
acquires an acceleration of 1 m/s2. The
mass of this body must be
(a) 10kg (b) 20kg
(c) 10 2 kg (d) 2 10 kg
85. Aconveyor belt is moving at a constant speed of 2m/s. Abox
is gently dropped on it. The coefficient of friction between
them is µ= 0.5. Thedistance that theboxwill moverelativeto
belt before coming to rest on it taking g = 10 ms–2, is
(a) 1.2m (b) 0.6m
(c) zero (d) 0.4m
86. A person of mass 60 kg is inside a lift of mass 940 kg and
presses the button on control panel. The lift starts moving
upwards with an acceleration 1.0 m/s2. If g = 10 ms–2, the
tension in the supporting cable is
(a) 8600N (b) 9680N
(c) 11000N (d) 1200N
87. The upper half of an inclined plane of inclination q is
perfectlysmooth while lower half is rough. Ablock
starting from rest at the top of the plane will again come to
rest at the bottom, if the coefficient of friction between the
block and lower half of the plane is given by
(a) m =
2
tan q
(b) m = 2 tan q
(c) m = tan q (d) m =
1
tan q
88. A bridge is in the from of a semi-circle of radius 40m. The
greatest speed with which a motor cycle can cross the bridge
without leaving the ground at the highest point is
(g = 10 m s–2) (frictional force isnegligiblysmall)
(a) 40 m s–1 (b) 20 m s–1
(c) 30 m s–1 (d) 15 m s–1](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-127-320.jpg)

![125
Lawsof Motion
Exemplar Questions
1. A ball is travelling with uniform translatory motion. This
means that
(a) it is at rest
(b) the path can be a straight line or circular and the ball
travels with uniform speed
(c) all parts of the ball have the same velocity(magnitude
and direction) and the velocity is constant
(d) the centre of the ball moves with constant velocityand
the ball spins about its centre uniformly
2. Ametre scale is moving with uniform velocity. This implies
(a) the force acting on the scale is zero, but a torque about
the centre of mass can act on the scale
(b) the force acting on the scale is zero and the torque
acting about centre of mass of the scale is also zero
(c) the total force acting on it need not be zero but the
torque on it is zero
(d) neither the force nor the torque need to be zero
3. A cricket ball of mass 150 g has an initial velocity
1
ˆ ˆ
(3 4 )ms
u i j -
= +
r
and a final velocity 1
ˆ ˆ
(3 4 )ms
v i j -
= - +
r
,
after beinghit. The changein momentum (final momentum-
initial momentum) is (in kgms–1)
(a) zero (b) ˆ ˆ
(0.45 0.6 )
i j
- +
(c) ˆ ˆ
(0.9 1.2 )
j j
- + (d) ˆ ˆ ˆ
5( )
i j i
- +
4. In the previous problem(3), the magnitude ofthemomentum
transferred during the hit is
(a) zero (b) 0.75 kg-m s–1
(c) 1.5 kg-m s–1 (d) 1.4 kg-m s–1
5. Conservation of momentum in a collision between particles
can be understood from
(a) Conservation of energy
(b) Newton's first law only
(c) Newton's second law only
(d) both Newton's second and third law
6. A hockey player is moving northward and suddenly turns
westward with the same speed to avoid an opponent. The
force that acts on the player is
(a) frictional force along westward
(b) muscle force along southward
(c) frictional force along sotuh-west
(d) muscle force along south-west
7. A body of mass 2 kg travels according to the law
2 3
( )
x t pt qt rt
= + + where, q = 4 ms–2, p = 3 ms–1 and r= 5
ms–3. The force acting on the body at t = 2s is
(a) 136N (b) 134N
(c) 158N (d) 68N
8. A body with mass 5 kg is acted upon by a force
ˆ ˆ
( 3 4 ) N
F i j
= - +
r
. If its initial velocity at t = 0 is
1
ˆ ˆ
(6 12 ) ms
v i j -
= - , the time at which it will just have a
velocity along the y-axis is
(a) never (b) 10 s
(c) 2 s (d) 15 s
9. A car of mass m starts from rest and acquires a velocity
along east, ˆ ( 0)
v vi v
= >
r
in two seconds. Assuming the
car moves with uniform acceleration, the force exerted on
the car is
(a)
2
mv
eastward and is exerted by the car engine
(b)
2
mv
eastward and is due to the friction on the tyres
exerted by the road
(c) more than
2
mv
eastward exerted due to the engine and
overcomes the friction of the road
(d)
2
mv
exerted by the engine
NEET/AIPMT (2013-2017) Questions
10. Three blocks with masses m, 2 m and 3 m are connected by
strings as shown in the figure. After an upward force F is
applied on block m, the masses move upward at constant
speed v. What is the net force on the block of mass 2m?
(g is the acceleration due to gravity) [2013]
(a) 2mg
(b) 3mg
(c) 6mg
(d) zero
11. A car is moving in a circular horizontal track of radius 10 m
with a constant speed of 10 m/s. A bob is suspended from
the roof of the car by a light wire of length 1.0 m. The angle
made bythe wire with the vertical is [NEET Kar. 2013]
(a) 0° (b)
3
p
(c)
6
p
(d)
4
p
12. A balloon with mass ‘m’ is descending down with an
acceleration ‘a’ (where a < g). How much mass should be
removed from it so that it starts moving up with an
acceleration ‘a’? [2014]
(a)
2ma
g a
+ (b)
2ma
g a
-
(c)
ma
g a
+
(d)
ma
g a
-](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-129-320.jpg)
![126 PHYSICS
13. Theforce‘F’ acting on a particle ofmass ‘m’ is indicated by
the force-timegraph shown below.Thechange in momentum
of the particle over the time interval from zero to 8 s is :
[2014]
6
3
0
–3
4 6 8
F(N)
t(s)
2
(a) 24 Ns (b) 20 Ns
(c) 12 Ns (d) 6 Ns
14. A system consists ofthree masses m1, m2 and m3 connected
by a string passing over a pulley P. The mass m1 hangs
freely and m2 and m3 are on a rough horizontal table (the
coefficient of friction = m). The pulleyis frictionless and of
negligible mass. The downward acceleration of mass m1 is :
(Assume m1 = m2 = m3 = m) [2014]
(a)
g(1 – g )
g
m
(b)
2g
3
m
P
m1
m2 m3
(c)
g(1 – 2 )
3
m
(d)
g(1 – 2 )
2
m
15. Three blocks A, B and C of masses 4 kg, 2 kg and 1 kg
respectively, are in contact on a frictionless surface, as
shown. If a force of 14 N is applied on the 4 kg block then
the contact force between A and B is [2015]
A B C
(a) 6N (b) 8N
(c) 18N (d) 2N
16. A block A of mass m1 rests on a horizontal table. A light
string connected to it passes over a frictionless pulley at
the edge of table and from its other end another block B of
mass m2 is suspended. The coefficient of kinetic friction
between the block and the table is µk. When the block A is
sliding on the table, the tension in the string is [2015]
(a)
2 1
1 2
(m – k m )g
(m m )
m
+ (b)
1 2 k
1 2
m m (1 )g
(m m )
+ m
+
(c)
1 2 k
1 2
m m (1 – )g
(m m )
m
+ (d)
2 k 1
1 2
(m m )g
(m m )
+ m
+
17. Two stones of masses m and 2 m are whirled in horizontal
circles, the heavier one in radius
r
2
and the lighter one in
radius r. The tangential speed of lighter stone is n times that
of the value of heavier stone when they experience same
centripetal forces. The value of n is : [2015 RS]
(a) 3 (b) 4
(c) 1 (d) 2
18. A plank with a box on it at one end is graduallyraised about
the other end.As the angle of inclination with the horizontal
reaches 30º the box starts to slip and slides 4.0 m down the
plank in 4.0s. The coefficients of static and kinetic friction
between the box and the plank will be, respectively :
[2015 RS]
mg
q
(a) 0.6 and 0.5 (b) 0.5 and 0.6
(c) 0.4 and 0.3 (d) 0.6 and 0.6
19. What is the minimum velocitywith which a bodyof mass m
must enter a vertical loop ofradius R sothat it can complete
the loop ? [2016]
(a) gR (b) 2gR
(c) 3gR (d) 5gR
20. One end of string of length l is connected to a particle of
mass 'm' and the other end is connected to a small peg on a
smooth horizontal table. If the particle moves in circle with
speed 'v' the net force on the particle (directed towards
centre) will be (T represents the tension in thestring) : [2017]
(a)
2
mv
T
l
+ (b) T –
2
mv
l
(c) Zero (d) T
21. Two blocks A and B of masses 3 m and m respectively are
connected bya massless and inextensible string. The whole
system is suspended by a massless spring as shown in
figure. The magnitudes of acceleration of A and B
immediatelyafter the string is cut, are respectively: [2017]
(a)
g
,g
3
A
B
3m
m
(b) g, g
(c)
g g
,
3 3
(d)
g
g,
3](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-130-320.jpg)
![127
Lawsof Motion
EXERCISE - 1
1. (c) 2. (b) 3. (d) 4. (a) 5. (c)
6. (a) 7. (a)
8. (d) Let n be the mass per unit length of rope. Therefore,
mass of rope = nL.
Acceleration in the rope due to force F will be
a= F/nL.
Mass of rope of length (L – l) will be n (L – l).
Therefore, tension in the rope oflength (L – l), is equal
to pulling force on it
= n (L – l) a = n (L – l) × F/nL = F (1 – l/L)
9. (a) Impulse = change in momentum = 1
2 v
m
v
m
r
r
-
10. (a) Let a be the acceleration of mass m2 in the downward
direction. Then
T – m2 (g/2) = m1 a ....(i)
and m2 g – T = m2 a ....(ii)
Adding eqs. (1) and (2), we get
(m1 + m2) a = m2g – m2 (g/2) = m2 g/2
)
m
m
(
2
g
m
a
2
1
2
+
=
11. (a) Let acceleration of a
lift = and
let reaction at spring balance = R
R
mg
Applying Newton’s law
R– mg = ma ( )
a
g
m
R +
=
Þ
thus net weight increases,
So reading of spring balance increases.
12. (b) See fig.
ma
mN
N
mg
If a = acceleration ofthe cart, then N = ma
mN = mg or m ma = mg or a = g/m
13. (c) p1 = mv northwards, p2 = mv eastwards
N
E
S
W
m
m
v
v
Let p = momentum after collision. Then,
2
1 p
p
p
r
r
r
+
= or 2
2
)
mv
(
)
mv
(
p +
=
r
2
mv
v
m
2 =
¢ or
2
v
v =
¢ m/sec
14. (c) Applying law of conservation of linear momentum
m1v1 + m2v2 = 0,
1
2
2
1
v
v
m
m
-
= or
1
2
2
1
m
m
v
v
-
=
15. (c) The equations of motion are
2 mg – T = 2ma
T– mg = ma Þ T= 4ma &a = g/3 soT =4mg/3
If pulley is accelerated upwards with an accleration a,
then tension in string is
)
a
g
(
3
m
4
T +
=
16. (b) Inertia is resistance to change.
17. (b) The time rate of change ofmomentum is force.
18. (a) At the highest point of the track,
2
mv '
N mg
r
+ =
mg
N
where r is the radius of curvature at that point and v¢ is
the speed of the block at that point.
Now
2
mv '
N mg
r
= -
N will be maximum when r is minimum (v¢ is thesame
for all cases). Of the given tracks, (a) has the smallest
radius of curvature at the highest point.
19. (c) f W
=m
f W tan
= q [ q
=
m tan ]
20. (a) )
1
n
2
(
2
a
Sn -
=
)
1
n
2
(
2
a
S 1
n +
=
+
1
n
2
1
n
2
S
S
1
n
n
+
-
=
+
21. (b) From the F.B.D.
N = mg cos q
F = ma = mg sin q – N
m
)
cos
(sin
g
a q
m
-
q
=
Þ
x
q
sin
g q
g
N
m
q
N
m m
mg
cos
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-131-320.jpg)
![128 PHYSICS
Now using, as
2
u
v 2
2
=
-
or, l
)
cos
(sin
g
2
v2
q
m
-
q
´
=
( l = length ofincline)
or, v = )
cos
(sin
g
2 q
m
-
q
l
22. (a) Based on Newton’s third law of motion.
23. (a) If m1, m2 are masses and u1, u2 are velocity then by
conservation of momentum m1u1 + m2u2 = 0 or
1 1 2 2
| m u | | m u |
=
24. (a) Here, on resolving force F2 and applying the concept
ofequilibrium
F1
F2sin q
F2
cos q
mg
N
f
m
q
+
= cos
F
mg
N 2 , and f = µN
]
cos
F
mg
[
f 2 q
+
m
= …(i)
Also q
+
= sin
F
F
f 2
1 …(ii)
From (i)and(ii)
]
cos
F
mg
[ 2 q
+
m = F1 + F2 sin q
Þ
q
+
q
+
=
m
cos
F
mg
sin
F
F
2
2
1
25. (a) The frictional force acting on M is µmg
Acceleration =
M
mg
m
EXERCISE - 2
1. (b) Here u = 10 ms–1, v = –2 ms–1,
t = 4 s, a = ?
Using 2
s
/
m
3
4
10
2
t
u
v
a -
=
-
-
=
-
=
Force, F =ma = 10×(–3) = –30 N
2. (b) 2 T cos 60º = mg
or T = mg = 2×10 = 20 N.
3. (c) If k is the spring factor, then P.E. of the spring
compressedbydistance x ÷
ø
ö
ç
è
æ
= 2
kx
2
1
will equal to gain
in P.E. of the dart ( = mgh) i.e. mgh
kx
2
1 2
=
200
g
16
)
4
(
k
2
1 2
´
´
= ....(i)
and h
g
16
)
6
(
k
2
1 2
´
´
= ...(ii)
On solving, (i) and (ii), weget h = 450 cm = 4.5m.
4. (d) Herem = 0.5 kg ; u = – 10 m/s ;
t = 1/50 s ; v = + 15 ms–1
Force = m (v– u)/t = 0.5 (10 + 15) × 50 = 625 N
5. (b) As, (1/2)m v2 = Fs
So 4
F
)
30
(
m
2
1 2
´
= and s
F
)
60
(
m
2
1 2
´
=
s/4 = (60)2 / (30)2 = 4 or s = 4 × 4 = 16 m.
6. (c) Acceleration, 2
v u 0 6
a 2 ms
t 3
-
- -
= = = -
Force= m×a =4×2= 8N
7. (a)
taken
time
momentum
in
change
required
Force =
=
3
(50 10 30) 400 (5 0)
10 N
60
-
´ ´ ´ - ´
=
8. (a) Changein momentum = Force × time =Area which the
force-time curve encloses with time axis.
9. (b) 20cm
10cm
32N(F )
2
20N(F )
1
l1 l2
L
F F
It is clear F2 > F1, so rod moves in right direction with
an acceleration a, whereas a is given by
(F2–F1)=mL×a................(i)
where m is mass of rod per unit length.
Now consider the motion of length l1 from first end,
then
F– F1=ml1a..................(ii)
Dividing eq (ii) by(i), we get
L
l
F
F
F
F 1
1
2
1
=
-
-
or 1
1
1
2 F
L
l
)
F
F
(
F +
´
-
=
here l1 = 10 cm., L= 30 cm., F1 = 20 N, F2 = 32N
so F = 24 N
10. (b) Change in momentum = F × t
= 10 × 10 = 100 Ns or 100 kg. m/s
11. (d) See fig.
1 kg
1 kg
T
T
T
From figure, 1 g – T = 1 a ...(i)
and T = 1 a ....(ii)
From eqs. (i) and (ii), we get
1g – 1a = 1a or 2a = g
a = (g/2) = (10/2) = 5 m/s2
So, T =ma = 1 ×5 = 5 N
12. (b) R= mg –ma = 0.5 × 10 – 0.5 × 2= 5 – 1= 4 N
13. (c) Seefig. Let Fbetheforce between theblocksand a their
common acceleration. Then for 2 kgblock,](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-132-320.jpg)


![131
Lawsof Motion
42. (d)
5
3
sin =
q
q
5
3
4
tan
4
3
=
q Þ
3
tan 0.75
4
m = q = =
43. (b) The condition to avoid skidding, v = rg
m
= 10
150
6
.
0 ´
´ = 30 m/s.
44. (d) Limitingfriction = 0.5 2 10 10N
´ ´ =
The applied force is lessthan force offriction, therefore
the force of friction is equal to the applied force.
45. (d) Applying law of conservation of momentum
Momentum of bullet = Momentum of sand-bullet
system
m m 21
v m V mV
20 20 20
æ ö
= + =
ç ÷
è ø
46. (d) Here 8
.
0
tan =
q
where q is angle of repose
°
=
=
q -
39
)
8
.
0
(
tan 1
The given angle of inclination is equal to the angle of
repose. So the 1 kg block has no tendency to move.
=
q
sin
mg force of friction
Þ T = 0
47. (d) For 0.5 kg block, 6 = 0.5 a
48. (b) While moving down, when the lift is accelerating the
weight will beless and when the lift is decelerating the
weight will be more.
49. (b) Total momentum = j
ˆ
p
î
p
2 +
Magnitude of total momentum
= p
5
p
5
p
)
p
2
( 2
2
2
=
=
+
This must be equal to the momentum ofthe third part.
50. (c)
90°
30°
M
mg sin 30°
ma cos 30°
30° 60°
ma (pseudo force)
a
°
=
° 30
sin
mg
30
cos
ma
3
g
a =
51. (d) Apparent weight when mass is falling down is given
by W ' m(g a)
= -
W ' 1 (10 10) 0
= ´ - =
52. (b) Reading of spring balance
2T =
1 2
1 2
4m m 4 5 1 10
m m 6 3
´ ´
= =
+
kgf
53. (a) a = 2v (given)
Þ
dv
v 2v
ds
=
or dv 2ds
=
v
0.1
0
0.1
dv 2[s] 0.2
= =
ò
v 0.1 0.2
- =
Þ 1
v 0.3ms-
=
54. (c) IfW is themaximum weight, then
W = 2T cos 60°
or W= T = 20N
55. (c) The acceleration of both the blocks =
15 5
3x x
=
Force on
5
B 2x 10 N
x
= ´ =
56. (b) The maximum acceleration that can be given is a
a
10
g
10
g
30 +
=
Þ 2
ms
20
g
2
a -
=
=
We know that
2
at
2
1
ut
s +
=
20
10
2
a
s
2
t
´
=
= = 1 s
57. (a) Let the air resistance be F. Then
mg F ma
+ = Þ ]
g
a
[
m
F -
=
Here
2
ms
12
5
.
2
30
a -
=
=
58. (c) N
30
1
.
0
)
20
0
(
15
.
0
t
)
u
v
(
m
F =
-
=
-
=
59. (c) Considering the two masses and the rope a system,
then
Initial net force = [ ]
25 (15 5) g 5g
- + =
Final net force = ( )
25 5 15 g 15 g
+ - =
é ù
ë û
Þ (acceleration)final = 3 (acceleration)initial
60. (d)
mg sin q
mg cos q
F cos q
q
F sin
F
mg
q
N
From figure q
+
q
= sin
F
cos
mg
N](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-135-320.jpg)



![135
Lawsof Motion
Presultant = 2 2
12 16
+
= 144 256
+ = 20
m3v3 = 20 (momentum ofthird part)
or, m3 =
20
4
= 5 kg
90. (b) Mg – T = Ma
T – mg = ma
m
mg mg
T
T
M
On solving, we get
a =
(M m)g
M m
-
+
and T =
2Mmg
M m
+
91. (c) Let velocity of bullet be v. If velocity of gun is V, then
mv + MV = 0
Þ V =
mv
M
-
As spring compresses by d, so
2 2
1 1
kd MV
2 2
=
or
2
2
1 1 mv
kd M
2 2 M
æ ö
= ç ÷
è ø
Þ v =
d
kM
m
92. (b) Here, l2 = 2l1
As for a spring, force constant
1
k
l
µ
1 2
1 2 1 2
1 1 1
, ,
k k k
l l l l
µ µ µ
+
1 1 2
1
k l l
k l
+
= and
2 1 2
2
k l l
k l
+
=
or
2
1
1
1
l
k k
l
é ù
+
= ê ú
ë û
and
1
2
2
1
l
k k
l
é ù
+
= ê ú
ë û
1 [1 2] 3
k k k
= + = [using (i)]
2
3
1
1
2
2
k k k
é ù
= =
+
ê ú
ë û
[using (i)]
93. (a) R = mg cos q –
2
mV
r
V
car
R
O
mg
q mg cos q
Over bridge
q
When q decreases, cosq increases i.e. R increases
94. (c) Impulse experienced by the body
= change in momentum = MV– (–MV) = 2MV.
95. (a) The force of friction on the chain lying on the table
should be equal to the weight of the hanging chain.
Let
r = mass per unit length of the chain
µ = coefficient of friction
l = length of the total chain
x = length of hanging chain
Now, µ(l – x) rg = xrg or µ(l – x) = x
or µl = (µ + 1)x or x = µl/(µ+ 1)
0.25 0.25
0.2
(0.25 1) 1.25
l l
x l
= = =
+
0.2 20%
x
l
= =
96. (a) Masses of the pieces are 1, 1, 3 kg. Hence
2 2 2
(1 21) (1 21) (3 )
V
´ + ´ = ´
That is, 7 2
V = m/s
97. (c)
2
1 1 2
2
2 1 2
K p m
K m p
= ´ [Q p = mv Þ
2
=
2
p
K
m
]
Hence,
1 1
2 2
1 1
4 2
p M
p M
= = =
98. (d) Work done in moving an object against gravitational
force depends only on the initial and final position of
the object, not upon the path taken. But gravitational
force on the bodyalong the inclined plane is not same
as that along the vertical and it varies with angle of
inclination.
99. (b) On a rainy day, the roads are wet. Wetting of roads
lowers the coefficient of friction between the types
and the road. Therefore, grip on a road of car reduces
and thus chances of skidding increases.
100. (a) The force acting on the body of mass M are its weight
Mg acting vertically downward and air resistance F
acting vertically upward.
Acceration of the body ,
M
F
g
a -
=
Now M > m, therefore, the bodywith larger mass will
have great acceleration and it will reach the ground
first.
EXERCISE - 3
Exemplar Questions
1. (c) In a uniform translatory motion if all the parts of the
body moves with (same velocity in same straight line,
so the velocity is constant.
A
v
v
v
The situation is shown in (figure) where a body A is in
unfirom translatory motion.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-139-320.jpg)
![136 PHYSICS
2. (b) According to question we have to apply Newton's
second law of motion, in terms of force and change in
momentum.
We know that
dp
F
dt
=
As given that the meter scale is moving with uniform
velocity, hence
Force (F) = m × 0 = 0
No change in its velocityi.e., acceleration of it zero by
Newton's second law.
Hence, net or resultant force must act on body is zero.
,
r F
t = ´
r
r r so,
As all part ofthe scale is moving with uniform velocity
and total force is zero, hence, torque will also be zero.
3. (c) As given that,
Mass of the ball = 150 g = 0.15 kg
ˆ ˆ
(3 4 ) m/s
u i j
= +
r
ˆ ˆ
(3 4 ) m/s
v i j
= - +
r
(Dp) Change in momentum
= Final momentum – Initial momentum
mv mu
= -
r r
ˆ ˆ ˆ ˆ
( ) (0.15)[ (3 4 ) (3 4 )]
m v u i j i j
= - = - + - +
r r
ˆ ˆ
(0.15)[ 6 8 ]
i j
= - -
ˆ ˆ
[0.15 6 0.15 8 ]
i j
= - ´ + ´
ˆ ˆ
[0.9 1.20 ]
i j
= - +
ˆ ˆ
[0.9 1.2 ]
p i j
D = - +
Hence verifies option (c).
4. (c) From previous solution
ˆ ˆ ˆ ˆ
(0.9 1.2 ) 0.9 1.2
p i j i j
D = - + = - -
Magnitude of
2 2
| | ( 0.9) ( 1.2)
p
D = - + -
0.81 1.44
= +
2.25 1.5
= = kg-m s–1
Verifies the option (c).
5. (d) By Newton's second law :
ext
dp
F
dt
=
r
As ext
F
r
in law of conservation of momentum is zero.
If 0, 0
ext
F dp p
= = Þ = constant
Hence, momentum of a system will remain conserve if
external force on the system is zero.
In case of collision between particle equal and opposite
forces will act on individual particle by Newton's third
law.
So, 12 21
F F
= -
r r
( 0)
ext
F =
r
Q
Total force on the system will be zero.
12 21
dp dp
dt dt
= -
r r
or 12 21
dp dp
= -
r r
12 21
( 0)
dp dp
Þ + =
r r
So prove the law of conservation of momentum and
verifies the option (d).
6. (c) Consider the adjacent diagram.
A
B
B O
E
S
N
P2
P2
P1
–
( )
W
P1
The force on player is due to rate of change of
momentum. The direction offorce acting on player will
be the same as the direction of change in momentum.
Let OA = P1 i.e., Initial momentumof player northward
AB = P2 i.e., Final momentum of player towards west.
Clearly, OB =OA +OB
Changein momentum
= P2 – P1
= AB – OA = AB + (–OA)
= Clearlyresultant AR will be along south-west.
So, it will be also the direction of force on player.
7. (a) As given that, mass = 2 kg
p = 3 m/s, q = 4 m/s2, r = 5 m/s3
As given equation is
2 3
( )
x t pt qt rt
= + +
2
( )
2 3
ds t
v p qt rt
dt
= = + +
2
2
( )
0 2 6
dv d x t
a q rt
dt dt
= = = + +
2
2
( 2)
( )
2 12
t
d x t
q r
dt =
é ù
= +
ê ú
ë û
2 12
q r
= +
=2 ×4 +12 ×5
= 8 + 60 = 68 m/s2
Force acting on body ( ) =
F ma
r
= 2 × 68= 136 N.
8. (b) As given that mass = m = 5 kg
Acting force = ˆ ˆ
( 3 4 ) N
F i j
= - +
r](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-140-320.jpg)

![138 PHYSICS
m1
m2
mk
m g
2
a
m g
1
mk
T
a
a = 2 k 1
1 2
m g – m g
m m
m
+
m2g – T = (m2)
2 k 1
1 2
m g – m g
m m
æ ö
m
ç ÷
+
è ø
solving we get tension in the string
T = 1 2 k
1 2
m m g (1 )g
m m
+ m
+
17. (d) According to question, two stones experience same
centripetal force
i.e. 1 2
C C
F F
=
or,
2 2
1 2
mv 2mv
r (r / 2)
= or, 2 2
1 2
V 4V
=
So, V1 = 2V2 i.e., n = 2
18. (a) Coefficient of static friction,
ms = tan 30°=
1
3
= 0.577@ 0.6
S = ut +
2
1
at
2
4 =
1
2
a(4)2 Þ a =
1
2
= 0.5
[Q s = 4m and t = 4s given]
a = gsinq – mk(g) cosq
Þ mk =
0.9
3
= 0.5
19. (d) To complete the loop a bodymust enter a vertical loop
ofradius R with the minimum velocity v= 5gR .
20. (d) Net force on particle in uniform circular motion is cen-
tripetal force
2
mv
l
æ ö
ç ÷
ç ÷
è ø
which is provided by tension in
string so the net force will be equal to tension i.e., T.
21. (a) m
mg
Before cutting the string
kx=T +3mg ...(i)
T = mg ...(ii)
Þ kx=4mg
After cutting the string T = 0
A
4mg 3mg
a
3m
-
=
4mg
A
g
a
3
=
and B
mg
a g
m
= =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-142-320.jpg)
![WORK
Work Done by a Constant Force
Work done (W) by a force F
ur
in displacing a body through a
displacement x is given by
W = F.x
r r
= Fx cos q
F
x
Body
F cos q
q
Fsinq
Where q istheanglebetween theappliedforce F
r
and displacement
x
r
.
The S.I. unit ofwork isjoule, CGS unit is erg and itsdimensions
are[ML2T–2].
1 joule = 107 erg
(a) When q = 0° then W = Fx
(b) When q is between 0 and p/2 then
W = Fx cos q = positive
(c) When q = p/2 then W = Fx cos 90° = 0 (zero)
Work done bycentripetal force is zero as in this case angle
q =90°
(d) When q is between / 2 and
p p then
W = Fx cos q = negative
Work Done by a Variable Force
When the force is an arbitrary function of position, we need the
techniques of calculus toevaluate the work done byit. The figure
shows Fx as function of the position x. We begin by replacing
the actual variation of the force by a series of small steps.
The area under each segment of the curveis approximatelyequal
tothe area ofa rectangle. The height ofthe rectangle is a constant
valueof force, and its width is a small displacement Dx. Thus, the
step involves an amount of work DWn = Fn Dxn. The total work
done is approximately given by the sum of the areas of the
rectangles.
i.e., W » n
F
å Dxn.
As the size of the steps is reduced, the tops of the rectangle more
closelytrace the actual curve shown in figure. Ifthe limit Dx ®0,
which is equivalent to letting the number ofsteps tend to infinity,
the discrete sum is replaced by a continuous integral.
0
lim
n
n n x
x
W F x F dx
D ®
= D =
å ò
Thus, the work done bya force Fx from an initial point A tofinal
point B is
n
A
x
A B x
x
W F dx
® = ò
The work done bya variable force in displacing a particle from x1
to x2
ò
=
2
1
x
x
Fdx
W = area under force displacement graph
CAUTION : When we find work, we should be cautious about
the question, work done bywhich force? Let us take an example
to understand this point. Suppose you are moving a body up
without acceleration.
Work done by applied force
app app
app
W F x F x
·
= =
uu
r uu
r
Work done by gravitational force x
mg
Fapplied
g
grav
W F x mgx
= = -
uuu
r uu
r uu
r
6
Work, Energy
and Power](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-143-320.jpg)

![142 PHYSICS
Then byrearranging equation (i), (iii) & (iv), we get
÷
÷
ø
ö
ç
ç
è
æ
´
÷
÷
ø
ö
ç
ç
è
æ
=
=
1
2
2
1
2
2
1
1
2
1
u
u
x
x
a
/
u
a
/
u
t
t
÷
÷
ø
ö
ç
ç
è
æ
=
´
=
Þ
2
2
1
1
1
2
2
2
2
2
1
1
2
1
u
M
u
M
u
u
)
u
M
(½
)
u
M
(½
t
t
(a) If
2
1
2
1
2
1
M
M
t
t
u
u =
Þ
=
(b) If
2
1
2
1
2
1
u
u
t
t
M
M =
Þ
=
(c) If M1u1 = M2u2 Þ t1 = t2
and
2
1 1 1 2 1 2
2
2 1 2 1
2 2
x (M u ) M x M
x M x M
(M u )
= ´ Þ =
(d) Consider two vehicles of masses M1 & M2
respectively.
Iftheyare moving with same velocities, then the ratio
of their stopping distances bythe application of same
retarding force is given by
2
1
2
1
M
M
x
x
= and let M2 > M1 then x1 < x2
Þ lighter mass will cover less distance then the
heavier mass
And the ratio of their retarding times are as follows :
2
1
2
1
M
M
t
t
= i.e
2
1
2
1
t
t
x
x
=
8. If kinetic energy of a body is doubled, then its momentum
becomes 2 times,
2
k k
p
E p E
2m
= Þ µ
9. If two bodies of masses m1 and m2 have equal kinetic
energies, then their velocities are inversely proportional
to the square root of the respective masses. i.e.
2 2
1 1 2 2
1 1
m v m v then
2 2
=
1
2
2
1
m
m
v
v
=
10. (a) The spring constant of a spring is inversely
proportional to the no. of turns i.e.
1
K
n
µ
or kn = const.
(b) Greater the no. of turns in a spring, greater will be the
work done i.e. W µ n
(c) The greater is the elasticity of the spring, the greater
is the spring constant.
11. Spring constant : The spring constant of a spring is
inversely proportional to length i.e.,
l
1
K µ or
Kl = constant.
(a) If a spring is divided into n equal parts, the spring
constant of each part = nK.
(b) If spring of spring constant K1, K2, K3 .......... are
connected in series, then effective force constant
......
K
1
K
1
K
1
K
1
3
2
1
eff
+
+
+
=
(c) If spring of spring constant K1, K2, K3........... are
connected in parallel, then effective spring constant
Keff = K1 + K2 + K3 +.............
POWER
Power of the body is defined as the time rate of doing work by
the body.
The average power Pav over the time interval Dt is defined by
av
W
P
t
D
=
D
...(i)
And the instantaneous power P is defined by
0
t
W dW
P Lim
t dt
d ®
D
= =
D
...(ii)
Power is a scalar quantity
The S.I. unit of power is joule per second
1 joule/sec = 1watt
The dimensions of power are [ML2T–3]
( . ) . .
dW d dS
P F S F F v
dt dt dt
= = = =
r
r
r r r r
(force is constant over a small time interval)
So instantaneous power (or instantaneous rate of working) of a
man depends not only on the force applied to body, but also on
the instantaneous velocity of the body.
Example1.
A metre stick of mass 600 mg, is pivoted at one end and
displaced through an angle of 60º. The increase in its
potential energy is (g = 10 ms–2)
(a) 1.5 J (b) 15 J
(c) 150 J (d) 0.15 J
Solution : (a)
G
M
O
h
60º
x
l/2
l
/
2
G´
A´
A
TheC.G. of stick rises from G toG´.
Increase in P.E. = mgh
= mg (l/2 –x) = (1 cos60º)
2
mg
-
l
J
5
.
1
2
1
1
2
1
x
10
x
6
.
0
=
ú
û
ù
ê
ë
é
-
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-146-320.jpg)






![150 PHYSICS
7. Amotor of 100 H.P. moves a load with a uniform speed of72
km/hr. The forward thrust applied by the engine on the car
is
(a) 1111N (b) 3550N
(c) 2222N (d) 3730N
8. Two bodies A and B having masses in the ratio of 3 : 1
possess the same kinetic energy. The ratio of linear
momentum of B toAis
(a) 1: 3 (b) 3: 1
(c) 1: 3 (d) 3 :1
9. When a U238 nucleus, originallyat rest, decays byemitting
an a-particle, saywith speed of vm/sec, the recoil speed of
the residual nucleus is (in m/sec.)
(a) – 4 v/234 (b) – 4 v/238
(c) 4v/238 (d) – v/4
10. Calculate the K.E and P.E. of the ball half way up, when a
ball of mass 0.1 kg is thrown vertically upwards with an
initial speed of 20 ms–1.
(a) 10 J, 20 J (b) 10 J, 10 J
(c) 15 J, 8 J (d) 8 J, 16 J
11. A spring of force constant 800 N/m has an extension of 5
cm. The work done in extending it from 5 cm to 15 cm is
(a) 16J (b) 8 J
(c) 32J (d) 24J.
12. Ifthe linear momentumisincreased by5%, the kineticenergy
will increase by
(a) 50% (b) 100%
(c) 125% (d) 10%
13. A cord is usedtolower verticallya block ofmass M, through
a distance d at a constant downward acceleration of g/8.
Then the work done by the cord on the block is
(a) Mg d/8 (b) 3 Mg d/8
(c) Mg d (d) – 7 mg d/8
14. Aforce F (5i 3j 2k)N
= + +
r r r
r
is appliedover a particlewhich
displaces it from its origin to the point r (2i j)m.
= -
r r
r
The
work done on the particle in joule is
(a) +10 (b) +7
(c) –7 (d) +13
15. A spring ofspring constant 5 × 103 N/m is stretched initially
by 5 cm from the unstretched position. Then the work
required to stretch it further by another 5 cm is
(a) 18.75J (b) 25.00J
(c) 6.25J (d) 12.50J
16. Two solid rubber balls A and B having masses 200 &
400 gm respectively are moving in opposite direction with
velocity of A equal to 0.3 m/sec. After collision the two
balls come to rest when the velocity of B is
(a) 0.15m/sec (b) 1.5m/sec
(c) –0.15m/sec (d) None of these
17. A bomb of mass 9 kg explodes into the pieces of masses
3 kg and 6 kg. The velocity of mass 3 kg is 16 m/s. The
kinetic energy of mass 6 kg in joule is
(a) 96 (b) 384
(c) 192 (d) 768
18. A long string is stretched by 2 cm and the potential energy
isV. If the spring is stretched by10 cm, its potential energy
will be
(a) V/25 (b) V/5
(c) 5V (d) 25V
19. When the kinetic energy of a body is increased to three
times, then the momentum increases
(a) 6 times (b) 1.732times
(c) 2 times (d) 2 times
20. Twobodies of masses 2 m and m have their KE in the ratio
8 : 1. What isthe ratio oftheir momenta ?
(a) 8: 1 (b) 4: 1
(c) 2: 1 (d) 1: 1
21. A body of mass 5 kg initially at rest explodes into 3
fragments with mass ratio3: 1 :1. Twoof fragments each of
mass ‘m’ are found tomove with a speed 60m/s in mutually
perpendicular directions. The velocityofthird fragment is
(a) 60 2 (b) 20 3
(c) 10 2 (d) 20 2
22. A machine, which is 75% efficient, uses 12 J of energy in
lifting up a 1 kg mass through a certain distance. The mass
is then allowed to fall through that distance. The velocity
at the end of its fall is (in m/s)
(a) 24 (b) 12
(c) 18 (d) 9
23. A body accelerates uniformly from rest to a velocity of 1
ms–1 in 15 seconds. The kinetic energyof the body will be
9
2
J when 't' is equal to [Take mass of body as 1 kg]
(a) 4s (b) 8s
(c) 10s (d) 12s
24. A machine gun fires a bullet of mass 40 g with a velocity
1200 ms–1. Theman holding it can exert a maximum forceof
144 N on the gun. Howmany bullets can he fire per second
at the most?
(a) 2 (b) 4
(c) 1 (d) 3
25. A crane is used to lift 1000 kg of coal from a mine 100 m
deep. The time taken bythe crane is 1 hour. The efficiency
of the crane is 80%. If g = 10 ms–2, then the power of the
crane is
(a) 104 W (b) 105 W
(c) W
8
36
104
´
(d) W
8
36
105
´
26. In figure, a carriagePis pulled up fromAto B. The relevant
coefficient of friction is 0.40. The work done will be
(a) 10kJ
(b) 23kJ
(c) 25kJ
P 50 kg
50
30 m
B
A
q
C
m
(d) 28kJ](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-154-320.jpg)
![151
Work, Energy and Power
27. A neutron with velocity v strikes a stationary deuterium
atom, its K.E. changes by a factor of
(a)
16
15
(b)
2
1
(c)
1
2
(d) None of these
28. A bodymoves a distance of10 m along a straight line under
the action of a force of 5 newtons. If the work done is 25
joules, the angle which the force makes with the direction
of motion of body is
(a) 0º (b) 30º
(c) 60º (d) 90º
29. A sphere of mass 8m collides elastically(in one dimension)
with a block ofmass 2m. If the initial energyof sphere is E.
What is the final energy of sphere?
(a) 0.8E (b) 0.36E
(c) 0.08E (d) 0.64E
30. Johnny and his sister Jane race up a hill. Johnny weighs
twice as much as jane and takes twice as long as jane to
reach the top . Compared to Jane
(a) Johnnydid more work and delivered more power.
(b) Johnnydid more work and delivered the same amount
of power.
(c) Johnny did more work and delivered less power
(d) Johnnydid less work and johnnydelivered less power.
31. A bodyof mass m moving with velocityv makes a head on
elastic collision with another body of mass 2m which in
initially at rest. The loss of kinetic energy of the colliding
body (mass m ) is
(a)
2
1
ofits initial kinetic energy
(b)
9
1 ofits initial kinetic energy
(c)
9
8
ofits initial kinetic energy
(d)
1
4
ofits initial kinetic energy
32. In the non-relativistic regime, ifthe momentum, is increase
by 100% , the percentage increase in kinetic energy is
(a) 100 (b) 200
(c) 300 (d) 400
33. A body is dropped from a height of 20m and rebounds to a
height 10m. The loss of energy is
(a) 10% (b) 45%
(c) 50% (d) 75%
34. A moving body with a mass m1 and velocity u strikes a
stationarybodyofmass m2. The masses m1 and m2 should
be in the ratio m1/m2 so as to decrease the velocity of the
first body to 2u/3 and giving a velocityofu to m2 assuming
a perfectly elastic impact. Then the ratio m1/m2 is
(a) 5 (b) 5
/
1
(c) 25
/
1 (d) 25.
35. A body of mass m is suspended from a massless spring of
natural length l. It stretches the spring through a vertical
distance y. The potential energy of the stretched spring is
(a) )
y
(
mg +
l (b) )
y
(
mg
2
1
+
l
(c) mgy
2
1
(d) mgy
36. Figure here shows the frictional force versus displacement
for a particle in motion. The loss of kinetic energy in
travelling over s = 0 to 20 m will be
15
10
5
0
0 5 10 20
x(m)
f(N)
(a) 250J (b) 200J
(c) 150J (d) 10J
37. Ten litreof water per second is lifted from a well through 10
m and delivered with a velocity of 10 ms–1. If
g = 10 ms–2 , then the power of the motor is
(a) 1 kW (b) 1.5kW
(c) 2 kW (d) 2.5kW
38. A nucleus ruptures into twonuclear parts which have their
velocity ratio equal to 1
:
2 . The ratio of their respective
nuclear sizes (nuclear radii )is
(a) 1: 2 (b) 2
:
1
(c) 1 : 21/3 (d) 1: 8
39. The rest energyofan electron is 0.511 MeV. The electron is
accelerated from rest to a velocity 0.5 c. The change in its
energywill be
(a) 0.026MeV (b) 0.051MeV
(c) 0.08MeV (d) 0.105MeV
40. A one-ton car moves with a constant velocity of
15 ms–1 on a rough horizontal road. The total resistance to
the motion of the car is 12% of the weight of the car. The
power required to keep the car moving with the same
constant velocity of 15ms–1 is
[Take g = 10 ms–2]
(a) 9 kW (b) 18kW
(c) 24kW (d) 36kW
41. Hail storms are observed to strike the surface of the frozen
lake at 300 with the vertical and rebound at 600 with the
vertical. Assume contact to be smooth, the coefficient of
restitution is
(a)
1
e
3
= (b)
1
e
3
=
(c) e 3
= (d) e = 3](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-155-320.jpg)
![152 PHYSICS
42. Abodystarts from rest and acquires a velocityV in time T.
Thework done on the bodyin time t will be proportional to
(a)
V
t
T
(b)
2
2
V
t
T
(c)
2
2
V
t
T
(d)
2
2
2
V
t
T
43. Aball isallowedtofall froma height of10 m. Ifthere is 40%
loss of energydue to impact, then after one impact ball will
go up to
(a) 10m (b) 8m
(c) 4m (d) 6m
44. The potential energy of a conservative system is given by
U = ay2 – by, where yrepresents the position of the particle
and a as well as bare constants. What is the force acting on
the system ?
(a) – ay (b) – by
(c) 2ay – b (d) b – 2ay
45. An automobile engine ofmass M accelerates and a constant
power p is applied bythe engine. The instantaneous speed
of the engine will be
(a) 1/ 2
[Pt / M] (b) 1/ 2
[2Pt / M]
(c) 1/ 2
[Pt / 2M] (d) 1/ 2
[Pt / 4M]
46. A bullet fired into a fixed target loses half of its velocity
after penetrating 3 cm. How much further it will penetrate
before coming to rest assuming that it faces constant
resistance to motion ?
(a) 2.0cm (b) 3.0cm
(c) 1.0cm (d) 1.5cm
47. A bomb of mass 16kg at rest explodes into two pieces of
masses 4 kg and 12 kg. The velolcity of the 12 kg mass is
4ms–1. The kinetic energy of the other mass is
(a) 144J (b) 288J
(c) 192J (d) 96J
48. Given that a force F̂ acts on a bodyfor time t, and displaces
the body by d̂ . In which of the following cases, the speed
of the body must not increase?
(a) F > d (b) F < d
(c) ˆ
F̂ d
= (d) ˆ
F̂ d
^
49. A body is attached to the lower end of a vertical helical
spring and it isgraduallyloweredto its equilibrium position.
This stretches the spring by a length x. If the same body
attached to the same spring is allowed to fall suddenly,
what would be the maximum stretching in this case?
(a) x (b) 2x
(c) 3x (d) x/2
50. A bag of mass M hangs by a long thread and a bullet (mass
m) comes horizontally with velocity V and gets caught in
the bag. Then for the combined (bag + bullet) system
(a)
mvM
momentum
M m
=
+
(b)
2
mV
kinetic energy
2
=
(c)
mV(M m)
momentum
M
+
=
(d)
2 2
m v
kinetic energy
2(M m)
=
+
51. Aparticle, initiallyat rest on a frictionless horizontal surface,
is acted upon by a horizontal force which is constant in
magnitude and direction. A graph is plotted of the work
done on the particle W, against the speed of the particle v.
Ifthere are no other horizontal forces acting on the particle,
the graph would look like
(a)
W
v
(b)
W
v
(c)
W
v
(d)
W
v
52. A particle of mass m moving eastward with a speed v
collides with another particle of the same mass moving
northwards with the same speed. If two particles coalesce
on collision, the new particle of mass 2 m will move in the
north-east direction with a velocity
(a) v / 2 (b) v 2
(c) v / 2 (d) None of these
53. A small block ofmass m is kept on a rough inclined surface
of inclination q fixed in an elevator. The elevator goes up
with a uniform velocity v and the block does not slide on
the wedge. The work done by the force of friction on the
block in time t as seen by the observer on the inclined p
lane will be
(a) zero (b) mgvt cos2q
(c) mgvt sin2 q (d) mgvt sin 2q
54. A nucleus moving with a velocity v
r
emits an a-particle.
Let the velocities ofthea-particle andtheremainingnucleus
be 1
v
r
and 2
v
r
and their masses be m1 and m2.
(a) v
r
, 1
v
r
and 2
v
r
must be parallel to each other
(b) None of the two of v
r
, 1
v
r
and 2
v
r
should be parallel to
each other
(c) 1 1 2 2
m v m v
+
r r
must be parallel to 1 2
(m m )v
+
r
.
(d) None of these
55. A shell is fired from a cannon with a velocityV at an angle
q with the horizontal direction. At the highest point in its
path, it explodes into two pieces of equal masses. One of
the pieces retraces its path to the cannon. The speed of the
other piece immediatelyafter the explosion is
(a) 3 V cos q (b) 2 V cos q
(c)
3
Vcos
2
q (d) V cos q](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-156-320.jpg)




![158 PHYSICS
17. Which ofthe diagrams in figure correctly shows the change
in kinetic energy of an iron sphere falling freely in a lake
having sufficient depth to impart it a terminal velocity?
(a)
KE
Depth
t
O
(b)
KE
Depth
t
O
(c)
KE
Depth
t
O
(d)
KE
Depth
t
O
18. A cricket ball of mass 150 g moving with a speed of 126 km/
h hits at the middle of the bat, held firmlyat its position by
the batsman. The ball moves straight back to the bowler
after hitting the bat. Assuming that collision between ball
and bat is completelyelastic and the two remain in contact
for 0.001s, the force that the batsman had to apply to hold
the bat firmly at its place would be
(a) 10.5N (b) 21N
(c) 1.05× 104 N (d) 2.1 × 104 N
NEET/AIPMT (2013-2017) Questions
19. A uniform force of ˆ ˆ
(3 )
i j
+ newton acts on a particle of
mass 2 kg. The particle is displaced from position $
(2 )
i k
$ +
meter to position $ $
(4 3 )
i j k
$ + - meter. The work done by
the force on the particle is [2013]
(a) 6 J (b) 13J
(c) 15J (d) 9 J
20. An explosion breaks a rock into three parts in a horizontal
plane. Two of them go off at right angles to each other. The
first part of mass 1 kg moves with a speed of 12 ms–1 and
the second part of mass 2 kg moves with speed 8 ms–1. If
the third part flies off with speed 4 ms–1 then its mass is
(a) 5 kg (b) 7 kg [2013]
(c) 17kg (d) 3 kg
21. A person holding a rifle (mass of person and rifle together
is 100 kg) stands on a smooth surface and fires 10 shots
horizontally, in 5 s. Each bullet has a mass of 10 g with a
muzzle velocityof 800 ms–1. The final velocityacquired by
the person and the average force exerted on the person are
[NEET Kar. 2013]
(a) –1.6 ms–1; 8 N (b) –0.08 ms–1;16N
(c) – 0.8 ms–1; 8 N (d) –1.6 ms–1; 16 N
22. Aparticlewith total energyE ismoving in apotentialenergy
region U(x). Motion ofthe particle is restricted tothe region
when [NEET Kar. 2013]
(a) U(x)> E (b) U(x)< E
(c) U(x)= O (d) U(x) £E
23. One coolie takes 1 minute to raise a suitcase through a
height of 2 m but the second coolie takes 30 s to raise the
same suitcase tothe same height. The powers of twocoolies
are in the ratio of [NEET Kar. 2013]
(a) 1: 2 (b) 1: 3
(c) 2: 1 (d) 3: 1
24. A bodyof mass (4m) is lying in x-yplane at rest. It suddenly
explodes into three pieces. Two pieces, each of mass (m)
move perpendicular to each other with equal speeds (v).
The total kinetic energy generated due to explosion is :
(a) mv2 (b)
2
3
mv
2
[2014]
(c) 2 mv2 (d) 4 mv2
25. A particle of mass m is driven bya machine that delivers a
constant power of k watts. If theparticle starts from rest the
force on the particle at time t is [2015]
(a) –1/2
mk t (b) –1/2
2mk t
(c)
–1/2
1
mk t
2
(d)
–1/2
mk
t
2
26. Two similar springs Pand Q have spring constants KP and
KQ, such that KP > KQ. They are stretched, first by the
same amount (case a,) then by the same force (case b). The
work done by the springs WP and WQ are related as, in
case (a) and case (b), respectively [2015]
(a) WP = WQ ; WP = WQ
(b) WP > WQ ; WQ > WP
(c) WP < WQ ; WQ < WP
(d) WP = WQ ; WP > WQ
27. A blockof mass 10 kg, moving in x direction with a constant
speed of 10ms–1, is subject toa retarding forceF =0.1 × J/m
during its travel from x = 20 m to 30 m. Its final KE will be:
(a) 450J (b) 275J [2015]
(c) 250J (d) 475J
28. The heart ofman pumps 5 litresofbloodthrough the arteries
per minute at a pressure of150 mm ofmercury. If the density
of mercury be 13.6 ×103 kg/m3 and g = 10m/s2 then the
power of heart in watt is : [2015 RS]
(a) 2.35 (b) 3.0
(c) 1.50 (d) 1.70](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-162-320.jpg)
![159
Work, Energy and Power
29. A ball isthrown verticallydownwards from a height of 20 m
with an initial velocity v0. It collides with the ground loses
50 percent of its energy in collision and rebounds to the
same height. The initial velocityv0 is : [2015 RS]
(Take g = 10 ms–2)
(a) 20 ms–1 (b) 28 ms–1
(c) 10 ms–1 (d) 14 ms–1
30. On a frictionless surfacea block of mass M moving at speed
v collides elastically with another block of same mass M
which is initiallyat rest.After collision thefirst block moves
at an angle q to its initial direction and has a speed
v
3
. The
second block's speed after the collision is : [2015 RS]
(a)
3
v
4
(b)
3
v
2
(c)
3
v
2
(d)
2 2
v
3
31. Two particles A and B, move with constant velocities 1
v
r
and 2
v
r
. At the initial moment their position vectors are 1
r
r
and 2
r
r
respectively. The condition for particlesAand Bfor
their collision is: [2015 RS]
(a) 1 1 2 2
r .v r .v
=
r r
r r
(b) 1 1 2 2
r v r v
´ = ´
r r
r r
(c) 1 2 1 2
r r v v
- = -
r r r r
(d) 1 2 2 1
1 2 2 1
r r v v
| r r | | v v |
- -
=
- -
r r r r
r r r r
32. A body of mass 1 kg begins to move under the action of a
time dependent force 2
ˆ ˆ
F (2ti 3t j)
= +
r
N, where î and ĵ are
unit vectors alogn x and y axis. What power will be
developed by the force at the time t? [2016]
(a) (2t2 + 3t3)W (b) (2t2 + 4t4)W
(c) (2t3 + 3t4) W (d) (2t3 + 3t5)W
33. Aparticle of mass10 gmovesalong acircleofradius 6.4cm
with a constant tangential acceleration. What is the
magnitude of this acceleration if the kinetic energy of the
particle becomes equal to 8 × 10–4 J by the end of the
second revolution after thebeginning ofthe motion ? [2016]
(a) 0.1m/s2 (b) 0.15 m/s2
(c) 0.18 m/s2 (d) 0.2m/s2
34. Consider a drop ofrain water having mass 1 g falling from a
height of 1 km. It hits the ground with a speed of 50 m/s.
Take 'g' constant with a value 10 m/s2.
The work done by the (i) gravitational force and the (ii)
resistive force of air is [2017]
(a) (i)1.25J (ii) –8.25J
(b) (i)100J (ii) 8.75J
(c) (i) 10J (ii) – 8.75 J
(d) (i) – 10 J (ii) –8.25J](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-163-320.jpg)


![162 PHYSICS
24. (d) Let n be the number of bullets that the man can fire in
one second.
change in momentum per second mv
n ´
= = F
[ m= mass of bullet, v = velocity] (Q F is the force)
1200
40
1000
144
mv
F
n
´
´
=
=
= 3
25. (d) Power supplied =
t
mgh
Power used by crane =
80
100
t
mgh
´
W
8
36
10
80
100
3600
100
10
1000 5
´
=
´
´
´
=
26. (b) Work done against gravity
Wg = 50 × 10 × 30 = 15 kJ
Work done against friction
Wf mgcos s
= m q´ =
4
0.4 50 10 50 8 kJ
5
´ ´ ´ ´ =
Total work done kJ
23
kJ
8
kJ
15
W
W f
g =
+
=
+
=
27. (d) Let mass of neutron = m
then mass of deuterium = 2m
[Q it has double nuclides thus has neutron].
Let initial velocityofneutron = v and final velocities
of neutron and deuterium are v1and v2 respectively.
m 2m
v=0
m 2m
v
1
v
® 2
v
®
neutron deuterium
Applying conservation of momentum
2
1 mv
2
mv
)
0
(
m
2
mv +
=
+
)
i
.(
..........
v
2
v
v 2
1 +
=
Þ
applying conservation of energy
2 2 2
1 2
1 1 1
mv mv 2m.v
2 2 2
= +
2 2 2
1 2
v v 2v ......(ii)
Þ = +
from (i)and (ii), 2
2
2
2
2
v
2
)
v
2
v
(
v +
-
=
2
2
2
2
2
2
2
v
2
v
v
4
v
4
v
v +
-
+
=
Þ
0
v
v
4
v
6 2
2
2 =
-
3
v
v
&
3
v
2
v 1
2 -
=
=
Þ
now fractional change in kinetic energy
i f
i
K K
K
-
=
2
2
1
2
mv
2
1
mv
2
1
mv
2
1
-
=
2
2
2
v
v
8
9
9
v
-
= =
28. (c) W = F s cos q, ,
2
1
10
5
25
s
F
W
cos =
´
=
=
q q = 60º.
29. (b) For elastic collision in one dimension
1
v =
2
1
2
2
m
m
u
m
2
+
+
)
m
m
(
u
)
m
m
(
2
1
1
2
1
+
-
As mass 2m, is at rest, So 2
u = 0
Þ 1
v =
m
2
m
8
u
)
m
2
m
8
(
+
-
= u
5
3
Final energy of sphere = f
.)
E
.
K
(
=
2
5
u
3
)
m
8
(
2
1
÷
ø
ö
ç
è
æ
=
2
2
5
3
u
)
m
8
(
2
1
÷
ø
ö
ç
è
æ
´
= E
25
9
=0.36E
30. (b) The work is done against gravity so it is equal to the
change in potential energy. W= Ep = mgh
For a fixed height, workisproportional toweight lifted.
Since Johnnyweighs twice as much as Jane he works
twice as hard to get up the hill.
Power is work done per unit time. For Johnny this is
W/Dt. Jane did half the work in half the time, (1/2 W)/
(1/2 Dt) = W/Dt which is the same power delivered by
Johnny.
31. (c) Fraction of energytransferred =
9
8
)
2
1
(
2
4
2
=
+
´
32. (c)
m
2
p
E
2
= Þ
2
2
2
1
2
1
p
p
E
E
= Þ 4
E
E 1
2 ´
=
1
1
2 E
3
E
E =
-
33. (c) Since the new height gained is half, therefore there is
50% loss of energy.
34. (a) u
m
3
u
2
m
u
m 2
1
1 +
= (By condition of linear
momentum)
Þ 1 2
1
m u m v
3
= ......(i)
Also
|
u
u
|
|
v
v
|
e
1
2
2
1
-
-
=
Þ
2u
v u
3
- = Þ
5
v u
3
= ......(ii)
From (i) and (ii), u
m
3
5
u
m
3
1
2
1 = Þ 5
m
m
2
1
=
35. (c) At Equilibrium , ky= mg Þ
y
mg
k =
mgy
2
1
y
y
mg
2
1
U 2
=
÷
÷
ø
ö
ç
ç
è
æ
=
36. (a) Loss in K.E =Area under the curve](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-166-320.jpg)
![163
Work, Energy and Power
37. (b) In this case, P =
t
mv
2
1
mgh 2
+
Þ
ú
ú
û
ù
ê
ê
ë
é
+
=
2
v
gh
t
m
P
2
Þ W
2
10
10
10
10
1
10
P ú
û
ù
ê
ë
é ´
+
´
= =1500W
38. (c) Byconservation of linear momentum,
1 2
2 1
m v
m v
=
or
2
1
r
3
4
r
3
4
3
2
x
3
x 1
=
p
r
p
r
Þ 3
/
1
2
1
2
1
r
r
=
39. (c)
2 2 2
0 0
2 2
2 2
m m
mc c c
v (0.5c)
1 1
c c
= =
- -
2
0
2
0
2
0
c
m
15
.
1
c
75
.
0
m
c
25
.
0
1
m
=
=
-
=
Change in energy = 1.15 m0c2 – m0c2
= 0.15 × 9.1 × 10–31 × (3× 108)2
= 12.285 × 10–15 J
MeV
10
6
.
1
10
285
.
12
13
15
-
-
´
´
=
=0.07678MeV
40. (b)
12
F 1000 10 N 1200 N
100
= ´ ´ =
P= Fv= 1200 N × 15 ms–1 = 18 kW.
41. (b) Components of velocity before and after collision
parallel to the plane are equal, So
vsin 60° = u sin 30°.......(1)
Componentsofvelocitynormal tothe plane are related
to each other
v cos 60° = e u (cos 30°) ........(2)
Þ cot 60° = e cot 30° Þ
cos60
e
cot30
°
=
°
Þ
3
3
1
e = Þ .
3
1
e =
42. (d) Work done on the body is gain in the kinetic energy.
Acceleration of the body is a = V/T.
Velocityacquired in time t is v = at
V
t
T
=
K.E. acquired µ v2. That is work done
2 2
2
V t
T
µ
43. (d) Kinetic energyof ball when reaching the ground
= mgh = mg× 10
Kinetic energyafter the impact
60
mg 10 6mg
100
= ´ ´ =
If the ball rises to a height h, then mgh = 6 mg.
Hence, h = 6 m.
44. (d)
dU
F b 2ay
dy
= - = -
45. (b) Fv = P . or
dv
M v P
dt
=
That is
P
vdv dt
M
=
ò ò
Hence 1/ 2
v [2Pt / M]
=
46. (c)
cm
3
u
2
u 0
v =
x
Case I :
3
.
a
.
2
u
2
u 2
2
=
-
÷
ø
ö
ç
è
æ
or –
4
u
3 2
= 2. a. 3 Þ a = –
8
u2
Case II :
2
2
u
0 ÷
ø
ö
ç
è
æ
- = 2. a. x or –
4
u2
= 2.
÷
÷
ø
ö
ç
ç
è
æ
-
8
u2
× x
Þ x=1cm
Alternative method : Let K be the initial energy and F
be the resistive force. Then according towork-energy
theorem,
W = DK
i.e.,
2
2
1 1 v
3F mv m
2 2 2
æ ö
= - ç ÷
è ø
2
1 1
3F mv 1
2 4
æ ö
= -
ç ÷
è ø
2
3 1
3F mv
4 2
æ ö
= ç ÷
è ø
...(1)
and
2
2
1 v 1
Fx m m(0)
2 2 2
æ ö
= -
ç ÷
è ø
i.e.,
2
1 1
mv Fx
4 2
æ ö
=
ç ÷
è ø
...(2)
Comparing eqns. (1) and (2)
F=Fx
or x=1cm](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-167-320.jpg)
![164 PHYSICS
47. (b) Let the velocity and mass of 4 kg piece be v1 and m1
and that of 12 kg piece be v2 and m2.
Applying conservation of linear momentum
m2v2 = m1v1
1
1 ms
12
4
4
12
v -
=
´
=
Þ
J
288
144
4
2
1
v
m
2
1
.
E
.
K 2
1
1
1 =
´
´
=
=
48. (d) Velocitywill increase when forceis along the direction
ofdisplacement i.e. d̂
F̂ = .
49. (b) When body is lowered gradually, its weight acts at
C.G. of the spring. When same bodyis allowed to fall
freely, the same weight acts at lower end of the spring.
In the latter case, original length (L) ofspring is double.
As DL µ L, therefore, DL becomes twice in second
casei.e. 2x.
50. (d) If V is velocity of combination (bag + bullet), then
from principle ofconservation of linear momentum
m v
(m M)V m v or V
(m M)
+ = =
+
2 2
2
1 m v
K.E. (m M)V
2 2(m M)
= + =
+
51. (c) Workdone W = [ML2 T–2]
It shows that 1 2 2
W (LT ) i.e. W v .
-
µ µ
graph between W & v is a parabola.
Alternatively:
According to work energy theorem
2
2
2
mv
2
1
mu
2
1
mv
2
1
W =
-
= (Q u = 0)
Þ W µ v2
52. (c) Applyingprinciple ofconservation of linear momentum
2 2
(2m)V (mv) (mv) mv 2
= + =
v 2 v
V
2 2
= =
53. (a) Since block does not slide on wedge so displacement
is zero & hence work done by force is zero.
f
m
gsinq
q
u
mg
54. (c) If mass of nucleus is m, mass of a particle is m1 &
mass of remaining nucleus is m2, then from the lawof
conservation of momentum.
nucleus
remaining
of
momentum
2
2
particle
of
momentum
1
1
nucleus
of
momentum
initial
v
m
v
m
v
m
r
r
r
+
=
a
55. (a) Let M be the mass of shell. Applying law of
conservation of linear momentum
MV cosq =
MV M
cos v
2 2
æ ö
- q +
ç ÷
è ø
ie, MV cos q +
M
2
Vcosq =
M
2
v
or v = 3 Vcosq .
56. (d) As bob B is of same material and same mass as the
bob A, therefore, on elastic collision, their velocities
are exchanged. BobAcomes to rest and B moves with
the velocity of A.
57. (c) As velocities are exchanged on perfectly elastic
collision, therefore masses of two objects must be
equal.
.
m
m
or
1
m
m
b
a
b
a
=
=
58. (c) a kx
= -
dv
kx
dt
Þ = -
Also
dv
dx
dt
or
v
dt
dx
=
=
v x
2
v 0
1
vdv
kx v dv kxdx
dx
= - Þ = -
ò ò
( )
2
2 2
2 1
kx
v v
2
- = - ( )
2
2 2
2 1
1 1 kx
m v v m
2 2 2
æ ö
-
Þ - = ç ÷
è ø
2
K x
D a
59. (c)
2
i 1 1
1
K m u ,
2
=
1
2
1
2
1
1
2
1
1
f u
m
m
m
m
v
,
v
m
2
1
K
+
-
=
=
Fractional loss
2
1
1
2
1
1
2
1
1
i
f
i
u
m
2
1
v
m
2
1
u
m
2
1
K
K
K
-
=
-
( )
( )2
2
1
2
2
1
2
1
2
1
m
m
m
m
1
u
v
1
+
-
-
=
-
=
( )2
2
1
2
1
m
m
m
m
4
+
=
m
m2 = ; nm
m1 =
( )2
i
f
n
1
n
4
K
K
1
+
=
-
Energytransfer is maximum when 0
Kf =
( )2
4n
1
1 n
=
+
2
4n 1 n 2n
Þ = + + Þ 0
n
2
1
n2
=
-
+
( ) 0
1
n 2
=
- 1
n = ie. m
m2 = , m
m1 =
Transfer will be maximumwhen both masses are equal
and one is at rest.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-168-320.jpg)
![165
Work, Energy and Power
60. (c) s
/
m
10
4
10
0
4
14
10
Vc =
+
´
+
´
= ; since spring force is
internal force.
61. (a) For inelastic collision, linear momentum is conserved
Þ 1
mv = 2
mv
2 Þ
2
v
v 1
2 =
Lossin K.E. = Gain in P.E.
= mgh
2
v
)
m
2
(
2
1
mv
2
1 2
2
2
1 =
-
Þ 4 mgh =
2
1
mv –
2
mv2
1 =
2
mv2
1
=
2
mv2
Þ h =
g
8
v2
62. (d) P F v
= ´ Þ P = F a t P t
µ
63. (c) g
h
2
tAB =
1
BC CB
2
2h
t t 2
g
2e h 2h
2 2e
g g
+ =
= =
h
h
A
B
h
1
2
D
C
g
h
2
e
2
t
t 2
DB
BD =
+
Total time taken by the body in coming to rest
.........
g
h
2
e
2
g
h
2
e
2
g
h
2 2
+
+
+
=
2
2h 2h
2e [1 e e .........]
g g
= + + + +
=
e
1
1
g
h
2
e
2
g
h
2
-
´
+
2h 1 e 1 e
t
g 1 e 1 e
+ +
é ù æ ö
= = ç ÷
ê ú
- -
ë û è ø
64. (d) Initially, mg
k
3 = or
3
mg
k =
New force constant of longer part
2
mg
3
mg
2
3
k
2
3
'
k =
´
=
=
Finally, mg
y
'
k =
cm
2
2
mg
mg
'
k
mg
y =
´
=
=
65. (d) kg
8
kg
8
.
0
10
m =
´
=
height ofiron chain = 5m
mgh 8 10 5
P W 40W
t 10
´ ´
= = =
66. (c) Bylaw of conservation ofmomentum,
Mu = MV + mv ....(i)
Also e = MV
Mv
Mu
|
u
u
|
|
v
v
|
2
1
2
1
-
=
Þ
-
-
....(ii)
From (i) and (ii), 2Mu = (M + m)v
Þ
2uM 2u
v v
m
M m
1
M
= Þ =
+
+
67. (d) Centripetal force =
R
mv2
R
aS
2
R
K
2
R
2
mv
2
1 2
=
=
÷
ø
ö
ç
è
æ
=
68. (a) As the block is at rest at P.
q
m
=
q cos
mg
sin
mg
dx
dy
slope
tan =
=
q
=
m
L
x
L
2
x
dx
d 2
=
÷
÷
ø
ö
ç
ç
è
æ
=
mg
mg cosq
mg sinq
q
N P
x
y
8
.
0
L
x
=
Þ x = 0.8× 10 = 8m
69. (d) Work done by centripetal force is zero.
70. (a)
dU
F
dx
= -
71. (c) Thechangein momentum in the ball after the collision
with surface is m(0–v) = –mv
Since n balls impinge elastically each second on the
surface, then rate ofchange of momentum of ball per
second is
mvn (consider magnitudeonly)
Now According to Newton’s second law
rate of change ofmomentum per second ofball = force
experienced by surface.
72. (d)
h=1.5m
The mass of water is m = 1 × 103 kg
The increase in potential energy of water is
= mgh =(1 × 103) (10)(1.5) = 15 kJ](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-169-320.jpg)

![167
Work, Energy and Power
85. (b) From law of conservation of momentum, before
collision and after collision linear momentum (p) will
be same.
or initial momentum = final momentum.
2
p
E
2m
=
According to question,
2
1 1 2
2
2 1 2
E p 2m
E 2m p
= ´
1
2
2
1
m
m
E
E
=
Þ [p1 = p2]
86. (b) 2
2
kx
2
1
mv
2
1
= Þ mv2 = kx2 or 0.5 × (1.5)2 = 50×x2
x=0.15m
87. (a) Clearly v1 = 2 ms–1, v2 = 0
m1 = m (say), m2 =2m
v1' = ?, v'2 = ?
e =
1 2
2 1
v ' v '
v v
-
- ....(i)
Byconservation of momentum,
2m= mv1' + 2mv2' ...(ii)
From (i), 0.5 =
2 1
v ' v '
2
-
v2' = 1 + v1'
From (ii), 2 = v1'+ 2 + 2 v1'
Þ v1 = 0 and v2 = 1 ms–1
88. (b) Power exerted by a force is given by
P= F.v
When the body is just above the earth’s surface, its
velocityis greatest.At this instant, gravitational force
is also maximum. Hence, the power exerted by the
gravitational force is greatest at the instant just before
the body hits the earth.
89. (a) As the two masses stick together after collision, hence
it is inelastic collision. Therefore, only momentum is
conserved.
2v
3m
v x
m
ˆ ˆ
mvi 3m(2v)j (4m)v
r
+ =
v 6
ˆ ˆ
v i vj
4 4
= +
r
=
v 3
ˆ ˆ
i vj
4 2
+
90. (b) For equilibrium
0
dU
dr
= Þ 3 2
2
0
A B
r r
-
+ =
r =
2A
B
for stable equilibrium
2
2
d U
dr
should be positive for the value of r.
here
2
2 4 3
6 2
d U A B
dr r r
= - is +ve value for
2A
r
B
= So
91. (d) Given : F
r
= 3i j
+
$ $
1
r
u
r
= $
( )
2i k
+
$ , 2
r
uu
r
= ( )
4i 3j k
+ -
r
$ $
r
r
= 2 1
r r
-
uu
r u
r
= ( )
4i 3j k
+ -
r
$ $ – $
( )
2i k
+
$
or r
r
= 2i 3j
+
$ $ – $
2k
So work done by the given force w = f.r
r r
= ( ) $
( )
3i j . 2i 3j 2k
+ + -
$ $ $ $ = 6 + 3 = 9J
92. (a)
4m
/sec
m
3
2 kg m2
Presultant
1 kg
x
y
8 m/sec
12 m/sec
m1
Presultant = 2 2
12 16
+
= 144 256
+ = 20
m3v3 = 20 (momentum ofthird part)
or, m3 =
20
4
= 5 kg
93. (c) p 2mK
=
p' 2m[K 3K]
= + = 2p
p 100 2p p
100 100%
p p
D ´ -
= ´ =
94. (c) Let m and v be the mass and the velocity of the body.
Then initial K.E. ,
Ki =
2
1
2
mv
Now, mass =
2
m
velocity = 2v](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-171-320.jpg)

![169
Work, Energy and Power
10. (b) As we know that,
W.D.
2 2
1 1
0
x x
x x
F dx ma dx
= × = ×
ò ò
uu
r uu
r
r r
As given that,
m = 0.5 kg, a = 5 m–1/2 s–1,
work done (W) = ?
3/2
v ax
=
We also know that,
Acceleration,
3/ 2 3/2
0 ( )
dv dv d
a v ax ax
dt dx dx
= = × =
3/ 2 1/2 2 2
3 3
2 2
ax a x a x
= ´ ´ ´ =
Now, Force =
2 2
0
3
2
ma m a x
=
From(i),
Work done
2
0
x
x
Fdx
=
=
= ò
2 2 2
0
3
2
ma x dx
é ù
= ê ú
ë û
ò
2
3
2
0
3
2 3
x
ma
æ ö
= ´ç ÷
ç ÷
è ø
2
1
8
2
ma
= ´
1
(0.5) (25) 8 50 J
2
= ´ ´ ´ =
11. (b) As given that power = constant
As we know that power (P)
dW F dx F dx
P
dt dt dt
×
= = =
uu
r
r
As the body is moving unidirectionally.
Hence, cos 0
F dx Fdx Fdx
× = ° =
constant
Fdx
P
dt
= = ( P =
Q constant by question)
Now, by dimensional formula
0
F v
× =
[F] [v] = constant
[MLT–2] [LT–1] = constant
[ML2T–3] = constant
3
2 T
L
M
=
(As mass of body constant)
2 3 3/ 2
L T L T
µ Þ µ Þ Displacement 3/2
( )
d t
µ
Verifies the graph (b).
12. (d) The speed of earth around the sun can never be zero
or negative, so the kinetic energy of earth cannot be
zero and negative.
So, option (b) and (c) represents wrongly the variation
in kinetic energy of earth.
A B
SUN
When the earth is closest to the sun, speed of the
earth is maximum, hence, KE is maximum. When the
earth isfarthest from the sun speed isminimum hence,
KEisminimum.
So, K.E. of earth increases (B to A) and then decrease,
variation is correctly represented by option (d).
13. (c) When a pendulum oscillates in air,due toair resistance
the force of friction acts between bob of pendulum
and air, so it will lose energy continuously in
overcoming. Therefore, total mechanical energy(KE
+ PE) of the pendulum decreases continuously with
time and finallybecomes zero.
Sum of KE and PE can never be negative. So, option
(a) and (d) are incorrect. Hence option (c) is verifies.
14. (a) As given that, mass (m) = 5 kg,
n = 300 revolution
Radius (R) =1 m
t = 60 sec
2
(300 2 )rad / 60s
n
t
p
æ ö
w = = ´ ´p
ç ÷
è ø
600
rad/s = 10 rad/s
60
´p
= p
linear speed (v) = wR = (10p× 1)
v = 10pm/s
KE
2
1
2
mv
=
2
1
5 (10 )
2
= ´ ´ p
2 1
100 5
2
= p ´ ´
2
250 J
= p
So, verifies the option (a).
15. (b) P.E. is maximum when drop start falling at
t = 0 as it fall is P.E. decrease gradually to zero. So, it
rejects the graph (a), (c) and (d).
K.E. at t = 0 is zero as drop falls with zero velocity, its
velocity increases (gradually), hence, first KE also
increases. After sometime speed (velocity) is constant
this is called terminal velocity, so, KE also become
constant. It happens when it falls
3
4
æ ö
ç ÷
è ø
height or
remains at
4
4
æ ö
ç ÷
è ø
from ground, then PE decreases
continuously as the drop is falling continuously.
Thevariation in PE and KE is best represented by(b).](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-173-320.jpg)







![179
System of Particles andRotationalMotion
(5)Annular disc (a) Perpendicular to plane
passing through centre
M
2
[ 2 2
1 2
R R
+ ]
2 2
1 2
R R
2
+
of mass
(b) Diameter in the plane
2 2
1 2
M[R R ]
4
+ 2 2
1 2
R R
4
+
(6) Hollowcylinder (a)Geometrical axis
2 2
1 2
R R
M
2
é ù
+
ê ú
ê ú
ë û
2 2
1 2
R R
2
+
(b) Perpendicular to length
passing through centre
2 2
2
1 2
(R R )
L
M
12 4
é ù
+
+
ê ú
ê ú
ë û
2 2
2
1 2
R R
L
12 4
+
+
of mass
(7) Solid sphere (a)Along the diameter
2
5
MR2
2
5
R
(b) Along the tangent
7
5
MR2
7
5
R
Ic
R1
R2 C
M
Ic
R1
R2
C
M
I
M
cm
L
R1
R2
M
cm
L
R1
R2
I
Ic
M
cm
R
Ic
M
cm
R
Id](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-183-320.jpg)
![182 PHYSICS
TORQUE, ANGULAR MOMENTUM AND ANGULAR
IMPULSE
Torque :
The moment of force is called torque. It is defined as the product
of force and the perpendicular distance of the force from the
axis of rotation.
O X
Y
q
q
r
F
i.e., r F
t = ´
r
r r
or, sin
rF
t = q
where q is the angle between r
r
and F
r
.
Its S.I. unit is (N-m). The dimensions of torque [ML2T–2] are
the same as that of energy but it is not energy.
Note : If the line of action of a force passes through axis of
rotation then no torque will be formed.
Angular Momentum:
The angular momentum ofa particle about an arbitrrypoint 'O' is
themoment of linear momentum taken about that point.
r
p
O X
Y
q
q
It is given as L r p
= ´
r r r
or, sin
L rp
= q
where q is the angle between r
r
and F
r
.
Angular Impulse :
2
1
2 1
t
t
J dt L L
= t = -
ò (= Change in angular momentum)
CONSERVATION OF ANGULAR MOMENTUM
From equation
dt
L
d
ext =
t
r
.
If constant
L
0
ext =
Þ
=
t
r
...(i)
This is called law of conservation of angular momentum.
According to this “if resultant external torque ext
t
r
acting on
the system is zero then total angular momentum of the system is
constant.
The magnitude of angular momentum for a system is given by
i
i
i
n
1
i
v
)
r
m
(
|
L
|
=
å
= w
å
=
=
)
r
m
( 2
i
i
n
1
i
[Q v = rw]
Þ w
=
w
´
å
=
=
I
)
I
(
|
L
| i
n
1
i
...(ii)
Where Ii is the moment ofinertia of the ith particle ofthat system
and I is total moment of inertia of the system
n
3
2
1
i
n
1
i
I
..........
..........
I
I
I
I
I +
+
+
+
=
å
=
=
or 2
n
n
2
2
2
2
1
1 r
m
..........
..........
r
m
r
m
I +
+
+
= ...(iii)
So if a system undergoes a redistribution of its mass, then its
moment of inertia changes but since noexternal torque is applied
on the system so total angular momentum is constant before and
after the distribution of mass, even if moment of inertia of the
system is changed.
Initial Final
L L
=
uu
r uu
r
...(iv)
or, I1w1 = I2w2 ...(v)
where L initial denote the state previous to the redistribution of
mass and final denote the state after the redistribution of mass in
that system.
Acomparisonof useful relationsin rotational andtranslational
or linear motion :
Rotational motion about Linear motion
a fixed axis
Angular velocity
d
dt
q
w = Linear velocity
dx
v
dt
=
Angular acceleration
d
dt
w
a = Linear acceleration
dv
a
dt
=
Resultant torque t = Ia Resultant force F = ma
Equations of rotational Equations of linear motion
motion
0
2
0 0
2 2
0 0
t
constant then t ½ t
2 ( )
w =w + a
ì
ï
ï
a = q -q = w + a
í
ï
w =w + a q -q
ï
î
2
2 2
v u at
1
a constant then s ut at
2
v u 2as
ì = +
ï
ï
= = +
í
ï
ï - =
î
where (s = x – x0)
Work
o
W d
q
q
= t q
ò
r
r
work
o
x
x
W Fdx
= ò
r r
Kinetic energy Ek = ½ Iw2 Kinetic energy Ek=½ mv2
Power P = tw Power P = Fv
rr
Angular momentum L = Iw
rr
Linear momentum p= mv
Torque
dL
dt
t = Force
dp
F
dt
=
Work EnergyTheoreminRotational Motion:
According to this theorem “the work done by external forces in
rotating a rigid body about a fixed axis is equal to the change
in rotational kinetic energy of the body.”](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-186-320.jpg)









![193
System of Particles andRotationalMotion
32. A composite disc is to be made using equal masses of
aluminiumandiron sothat it has ashigh a moment ofinertia
as possible. This is possible when
(a) thesurfaces ofthediscare madeofiron with aluminium
inside
(b) the whole ofaluminium is kept in the core and the iron
at the outer rim of the disc
(c) the whole of the iron is kept in the core and the
aluminium at the outer rim of the disc
(d) the whole disc is made with thin alternate sheets of
iron and aluminium
33. A ball rolls without slipping. The radius of gyration of the
ball about an axis passing through its centre of mass is K. If
radius of the ball be R, then the fraction of total energy
associated with its rotational energywill be
(a) 2
2
2
R
K
R
+
(b) 2
2
2
R
R
K +
(c) 2
2
R
K
(d) 2
2
2
R
K
K
+
34. When a bucket containing water is rotated fast in a vertical
circle of radius R, the water in the bucket doesn't spill
provided
(a) thebucket is whirled with a maximum speedof 2gR
(b) the bucket is whirled around with a minimum speed of
]
gR
)
2
/
1
[(
(c) the bucket is having a rpm of )
R
/(
g
900 2
p
(d) the bucket is having a rpm of )
R
/(
g
3600 2
p
35. A coin placed on a gramophone record rotating at
33 rpm flies off the record, if it is placed at a distance of
more than 16 cm from the axis of rotation. If the record is
revolving at 66 rpm, the coin will fly off if it is placed at a
distance not less than
(a) 1cm (b) 2cm
(c) 3cm (d) 4cm
36. Two fly wheels A and B are mounted side by side with
frictionless bearings on a common shaft. Their moments of
inertia about the shaft are 5.0 kg m2 and 20.0 kg m2
respectively. Wheel Ais madeto rotate at 10 revolution per
second. Wheel B, initially stationary, is now coupled to A
with the help of a clutch. The rotation speed of the wheels
will become
(a) 2 5 rps (b) 0.5rps
(c) 2 rps (d) None of these
37. A wheel is rolling straight on ground without slipping. If
the axis of the wheel has speed v, the instantenous velocity
of a point P on the rim, defined by angle q, relative to the
ground will be
(a) ÷
ø
ö
ç
è
æ
q
2
1
cos
v
(b) ÷
ø
ö
ç
è
æ
q
2
1
cos
v
2
q
P
(c) )
sin
1
(
v q
+
(d) )
cos
1
(
v q
+
38. Acertain bicycle can go up a gentle incline with constant
speed when the frictional force of ground pushing the rear
wheel is F2 = 4 N. With what forceF1 must the chain pull on
the sprocket wheel if R1=5 cm and R2 = 30 cm?
Road
Chain F1
R2
R1
F = 4N
2
Horizontal
(a) 4N (b) 24N
(c) 140N (d)
4
35
N
39. Auniform rod of length l is free torotate in a vertical plane
about a fixed horizontal axis through O. The rod begins
rotating from rest from its unstable equilibrium position.
When it has turned through an angle q, its angular velocity
w is given as
q
O
(a) q
sin
g
6
l
(b)
2
sin
g
6 q
l
(c)
2
cos
g
6 q
l
(d) q
cos
g
6
l
40. A sphere of mass 2000 g and radius 5 cm is rotating at the
rate of 300 rpm .Then the torque required to stop it in 2p
revolutions, is
(a) 1.6 × 102 dyne cm (b) 1.6 × 103 dyne cm
(c) 2.5 × 104 dyne cm (d) 2.5 × 105 dyne cm
41. Five masses are placed in a plane as shown in figure. The
coordinates of the centre of mass are nearest to
y
2 3 kg
5 kg
2 kg
1 kg
4 kg
1
0
0 2
x
1
(a) 1.2,1.4 (b) 1.3,1.1
(c) 1.1,1.3 (d) 1.0,1.0](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-197-320.jpg)



![197
System of Particles andRotationalMotion
Exemplar Questions
1. For which ofthe following does the centre ofmass lie outside
the body?
(a) A pencil (b) A shotput
(c) A dice (d) A bangle
2. Which of the following points is the likely position of the
centre of mass of the system shown in figure?
A
B
C
D
Hollow sphere
Air
R/2
R/2
Sand
(a) A (b) B
(c) C (d) D
3. A particle of mass m is moving in yz-plane with a uniform
velocity v with its trajectory running parallel to +ve y-axis
and intersecting z-axis at z = a in figure. The change in its
angular momentum about the origin as it bounces elastically
from a wall at y = constant is
(a) ˆ
mva x
e
v
z
a
y
(b) ˆ
2mva x
e
(c) ˆ
ymv x
e
(d) ˆ
2ymv x
e
4. When a disc rotates with uniform angular velocity, which of
the following is not true?
(a) The sense of rotation remains same
(b) The orientation of the axis of rotation remains same
(c) The speed of rotation is non-zero and remains same
(d) The angular acceleration is non-zero and remains same
5. A uniform square plate has a small piece Q of an irregular
shape removed and glued to the centre of the plate leaving
a hole behind in figure. The moment of inertia about the z-
axis is then,
Q
P
y
x
Q
P
y
x
hole
(a) increased
(b) decreased
(c) the same
(d) changed in unpredicted manner
6. In problem-5, the CM of the plate is now in the following
quadrant of x-y plane.
(a) I (b) II
(c) III (d) IV
7. The density of a non-uniform rod of length 1 m is given by
r(x) = a (1 + bx2) where, a and b are constants and
0 1.
x
£ £ The centre of mass of the rod will be at
(a)
3(2 )
4(3 )
b
b
+
+
(b)
4(2 )
3(3 )
b
b
+
+
(c)
3(3 )
4(2 )
b
b
+
+
(d)
4(3 )
3(2 )
b
b
+
+
8. A merry-go-round, made of a ring-like platform ofradius R
and mass M, is revolving with angular speed w.Aperson of
mass M is standing on it. At one instant, the person jumps
off the round, radially awayfrom the centre ofthe round (as
seen from the round). The speed ofthe round of afterwards
is
(a) 2w (b) w
(c)
2
w
(d) 0
NEET/AIPMT (2013-2017) Questions
9. A small object of uniform densityrolls up a curved surface
with an initial velocity ‘n’.Itreachesuptoamaximum height
of
2
3
4g
n
with respect to the initial position. The object is a
(a) solid sphere (b) hollow sphere [2013]
(c) disc (d) ring
10. A rod PQ of mass M and length L is hinged at end P. The
rod is kept horizontal bya massless string tied topoint Q as
shown in figure. When string is cut, the initial angular
acceleration of the rod is [2013]
(a) g /L (b) 2g/L
(c)
2
3
g
L
(d)
3
2
g
L](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-201-320.jpg)
![198 PHYSICS
11. Twodiscs are rotating about their axes, normal to the discs
and passing through the centres of the discs. Disc D1 has
2 kg mass and 0.2 m radius and initial angular velocityof 50
rads–1.DiscD2 has4kgmass,0.1mradiusandinitialangular
velocityof 200 rad s–1. The twodiscs are brought in contact
faceto face, with their axes of rotation coincident. The final
angular velocity (in rad s–1) of the system is
(a) 40 (b) 60 [NEET Kar. 2013]
(c) 100 (d) 120
12. The ratioof radii ofgyration of a circular ring and a circular
disc, of the same mass and radius, about an axis passing
through their centres and perpendicular to their planes are
(a) 2 :1 (b) 1: 2 [NEET Kar. 2013]
(c) 3: 2 (d) 2: 1
13. The ratio of the accelerations for a solid sphere (mass ‘m’
and radius ‘R’) rolling down an incline ofangle‘q’ without
slipping and slipping down the incline without rolling is :
(a) 5: 7 (b) 2: 3 [2014]
(c) 2: 5 (d) 7: 5
14. A solid cylinder of mass 50 kg and radius 0.5 m
is free to rotate about the horizontal axis.A massless string
is wound round the cylinder with one end attached to it
and other hanging freely. Tension in the string required to
produce an angular acceleration of 2 revolutions s– 2 is :
(a) 25N (b) 50N [2014]
(c) 78.5N (d) 157N
15. Threeidentical spherical shells, each ofmass m and radius
r are placed as shown in figure. Consider an axis XX' which
is touching to two shells and passing through diameter of
third shell. Moment of inertia of the system consisting of
these three spherical shells about XX' axis is [2015]
(a) 3mr2
(b) 2
16
mr
5
X
X¢
(c) 4mr2
(d)
2
11
mr
5
16. A rod of weight W is supported bytwo parallel knife edges
A and B and is in equilibrium in a horizontal position. The
knives are at a distance d from each other. The centre of
mass ofthe rod is at distance x fromA. The normal reaction
on A is [2015]
(a)
Wd
x
(b)
W(d – x)
x
(c)
W(d – x)
d
(d)
Wx
d
17. A mass m moves in a circle on a smooth horizontal plane
with velocity v0 at a radius R0. The mass is attached to
string which passes through a smooth hole in the plane as
shown.
v0
m
The tension in the string is increased graduallyand finally
m moves in a circle of radius 0
R
2
. The final value of the
kineticenergy is [2015]
(a)
2
0
1
mv
4
(b) 2
0
2mv
(c)
2
0
1
mv
2
(d) 2
0
mv
18. A force ˆ ˆ ˆ
F i 3j 6k
= a + +
r
is acting at a point
ˆ ˆ ˆ
r 2i 6j 12k
= - -
r
. The value of a for which angular
momentum about origin is conserved is : [2015 RS]
(a) 2 (b) zero
(c) 1 (d) –1
19. Point masses m1 and m2 are placed at the opposite ends of
a rigid rod oflength L, and negligible mass. The rod is to be
set rotating about an axis perpendicular to it. The position
of point P on this rod through which the axis should pass
sothat the work required to set the rod rotating with angular
velocity w0 is minimum, is given by: [2015 RS]
m1 m2
w0
P
x (L–x)
(a)
1
2
m
x L
m
= (b)
2
1
m
x L
m
=
(c)
2
1 2
m L
x
m m
=
+ (d)
1
1 2
m L
x
m m
=
+
20. An automobile moves on a road with a speed of 54 km h-1.
The radius of its wheels is 0.45 m and themoment ofinertia
of the wheel about its axis of rotation is 3 kg m2. If the
vehicle is brought to rest in 15s, the magnitude of average
torque transmitted byits brakes to the wheel is : [2015 RS]
(a) 8.58 kg m2 s-2 (b) 10.86 kg m2 s-2
(c) 2.86 kg m2 s-2 (d) 6.66 kg m2 s-2](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-202-320.jpg)
![199
System of Particles andRotationalMotion
21. A disk and a sphere of same radius but different massesroll
off on two inclined planes of the same altitude and length.
Which one of the two objects gets to the bottom of the
plane first ?
(a) Disk [2016]
(b) Sphere
(c) Both reach at the same time
(d) Depends on their masses
22. A uniform circular disc of radius 50 cm at rest is free toturn
about an axis which is perpendicular to its plane and passes
through its centre. It is subjected toa torque which produces
a constant angular acceleration of 2.0 rad s–2. Its net
acceleration in ms–2 at the end of2.0s is approximately:
(a) 8.0 (b) 7.0 [2016]
(c) 6.0 (d) 3.0
23. FromadiscofradiusRandmassM,acircular holeofdiameter
R, whose rim passes through the centre is cut. What is the
moment of inertia of the remaining part of the disc about a
perpendicular axis, passing through the centre ? [2016]
(a) 15 MR2/32 (b) 13 MR2/32
(c) 11 MR2/32 (d) 9 MR2/32
24. Which of the following statements are correct ? [2017]
(A) Centre of mass of a body always coincides with the
centre of gravity of the body
(B) Centre ofmass ofa bodyis the point at which the total
gravitational torque on the body is zero
(C) A couple on a body produce both translational and
rotation motion in a body
(D) Mechanical advantage greater than one means that
small effort can be used to lift a large load
(a) (A) and (B) (b) (B) and(C)
(c) (C) and(D) (d) (B) and (D)
25. Two discs of same moment of inertia rotating about their
regular axis passing through centre and perpendicular to
the plane of disc with angular velocities w1 and w2 . They
are brought into contact face to face coinciding the axis of
rotation. The expression for loss of energy during this
process is:- [2017]
(a)
2
1 2
1
I( )
4
w - w (b) 2
1 2
I( )
w - w
(c)
2
1 2
1
( )
8
w - w (d) 2
1 2
1
I( )
2
w + w
26. A rope is wound around a hollow cylinder ofmass 3 kg and
radius 40 cm. What is the angular acceleration of the
cylinder if the rope is pulled with a force of 30 N ? [2017]
(a) 0.25 rad/s2 (b) 25 rad/s2
(c) 5 m/s2 (d) 25 m/s2](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-203-320.jpg)
![200 PHYSICS
EXERCISE - 1
1. (a) 2. (b) 3. (c) 4. (c)
5. (b) 6. (d) 7. (b)
8. (d) The pull of earth changes onlywhen the body moves
sothat g changes. It is an exceptional case and should
not be considered unless otherwise mentioned.
9. (b) Ifwe applya torqueon a body, then angular momentum
of the body changes according to the relation
dL
τ
dt
=
r
r
Þ if t
r
= 0 then, L = constant
10. (b) Angular momentum L
r
is defined as L r m(v)
= ´
r r r
so L
r
is, an axial vector.
.
11. (c) The boy does not exert a torque to rotating table by
jumping, so angular momentum is conserved i.e.,
dL
0 L
dt
= Þ
r
r
= constant
12. (b) Since no external torque act on gymnast, so angular
momentum (L=Iω)isconserved.After pullingher arms
& legs, the angular velocity increases but moment of
inertia of gymnast, decreases in, such a way that
angular momentum remains constant.
13. (a)
14. (b) Angularmomentum willremainthesamesinceexternal
torque is zero.
15. (a)
2 2
B A
1
I MR I MR
2
= =
A B
I I
<
16. (a) Angular momentum ( )
r linear momentum
= ´
r
17. (b) We know that ext
dL
τ
dt
=
ifangular momentum is conserved, it means change in
angular momentum = 0
0
dL
,
or = , ext
dL
0 τ 0
dt
= Þ =
Thus total external torque = 0.
18. (a) Analogue of mass in rotational motion is moment of
inertia. It plays the same role as mass plays in
translational motion.
19. (a) Basic equation of moment of inertia is given
by 2
i
i
n
1
i
r
m
I
=
S
=
i
m
i
r
where i
m is the mass of th
i particle at a distance of
i
r from axis ofrotation.
Thus it does not depend on angular velocity.
20. (d) Initially centre of gravity is at the centre. When sand
is poured it will fall and again after a limit, centre of
gravitywill rise.
21. (d) Here, the centre of mass of the system remains
unchanged. in the horizontal direction. When the mass
m moved forward by a distance L cos q, let the mass
(m + M) moves by a distance x in the backward
direction. hence
(M + m) x – m L cos q = 0
x = (m L cos q)/(m + M)
22. (b) Acceleration of solid sphere is more than that of
hollow sphere, it rolls faster, and reaches the bottom
oftheinclined planeearlier.
Hence, solid sphere and hollow sphere can be
distinguished by rolling them simultaneously on an
inclined plane.
23. (d) Applying the law of conservation of momentum
m v= M V ...(1)
Byconservation of angular momentum
2
M L
m v(L / 2) ω
12
æ ö
= ç ÷
ç ÷
è ø
...(2)
As the collision is elastic, we have
2 2 2
1 1 1
m v M V Ι ω
2 2 2
= + ...(3)
Substituting the values, we get m = M/4
24. (b) a is propotional to w
Let a= kw (Qk is a constant)
dω
kω
dt
= [also
dθ dθ
ω dt
dt ω
= Þ = ]
ωdω
kω
dθ
= Þ dw= kdq
Now
ω/ 2
ω
dω k dθ
=
ò ò
0 θ
1
ω/2 0
ω ω
dω k dθ kθ kθ
2 2
= Þ - = Þ - =
ò ò
(Qq1 = 2pn)
θ = 1
θ or 2pn1 = 2pn
n1 = n
25. (b) Sorawegg islikea spherical shell &hard bioled egg is
like solid sphere. Let 1
I , 2
I be M. I. of raw egg and
boiled egg respectively.
Given that angular momentum L, is same
I1w1= I2w2 Þ w2>w1 QI1>I2
Nowfrom first equation ofangular motion (wf=wi+at)
here a is retarding decceleration for both cases &
wf = 0 for both case.
So 1 1 1
2 2 2
t (raw egg) ω / α t
1
t (hard egg) ω / α t
= Þ <
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-204-320.jpg)

![202 PHYSICS
11. (b) Moment of inertia (M.I) ofcircular ring I1 = mr2
moment of inertia (M.I) of circular disc I2 = ½mr2
1
2
I
I
2
1
=
Þ
12. (a) Tension provides the necessary centripetal force for
the rest of rod.
13. (d) Centrifugal force is observed when the observer is in
a frameundergoing circular motion.
14. (d)
2
1
mR
2
I =
2
M t R
µ µ
For disc X,
2
X
1
Ι (m)(R)
2
= =
2 2
1
(πr t).(R)
2
for discY, 2 2
Y
1
Ι [π(4R) .t / 4][4R]
2
=
Þ X
3
Y
Ι 1
Ι (4)
= Þ Y X
I 64 I
=
15. (a)
1
Angular momentum
Angular frequency
µ
Kinetic energy
µ
Þ
K.E.
L
ω
=
r
1 1 2
2 1 2
L K.E ω
4
L ω K.E
æ ö
= ´ =
ç ÷
è ø Þ 2
L
L
4
=
16. (a) When q = 0°, the net force is directed vertically
upwards.
17. (a) Let velocity at A
v
A = and velocity at B
v
B =
A
T
r
B
B
v
A
v
Applying conservation of energy at A & B
2
B
2
A mv
2
1
gmr
2
mv
2
1
=
+ [Q (P.E)A = mg (2r)]
)
i
(
..........
gr
4
v
v 2
A
2
B +
=
Nowas it is moving in circular path it has centripetal
force.
At point A
r
mv
mg
T
2
A
=
+
Þ
0
T
velocity
minimum
for ³
2
2
A
A
mv
or mg v gr
r
³ Þ ³ gr
vA ³
Þ
18. (a) A couple consists of two equal and opposite forces
whose lines of action are parallel and laterally
separated by same distance. Therefore, net force (or
resultant) of a couple is null vector, hence no
translatory motion will be produced and only
rotational motion will be produced.
19. (b) Angular momentum of mass mmoving with a constant
velocity about origin is
line parallel
to x-axis
v
m
O
y
x
L = momentum × perpendicular distance of line of
action ofmomentum from origin
L= mv × y
In the given condition mvy is a constant. Therefore
angular momentum is constant.
20. (c) Since the spheres are smooth, there will benotransfer
of angular momentum from the sphereA tosphere B.
The sphereAonlytransfers its linear velocityv to the
sphere B and will continue to rotate with the same
angular speed w.
21. (c)
2
)
ŷ
x̂
(
n̂
+
-
= –a cos45 x
o
–a sin45 y
o
45o
a
2
ˆ ˆ
v 4 (x y)
ˆ
a n
r 4 2
- +
= = ´
u
r
22. (b) Since v is changing (decreasing), L is not conserved
in magnitude. Sinceit isgiven that a particle isconfined
to rotate in a circular path, it can not have spiral path.
Since the particle has two accelerations ac and at
thereforethenet acceleration is not towards thecentre.
L ac
at
v
The direction of L remains same even when the
speed decreases.
23. (a) Themoment ofinertia (I) ofcircular ring whose axis of
rotation is passing through its center, 2
1
1 R
m
I =
Also, 2
2
2 )
nR
(
m
I =
Since both rings have same density,
1
1
2
2
A
R
2
m
A
)
nR
(
2
m
´
p
=
´
p
Þ](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-206-320.jpg)


![205
System of Particles andRotationalMotion
43. (a) So couple about the C.M must be zero for rotational
equilibrium, It means that
6
L
x
x
4
W
3
2
L
4
W
=
Þ
´
=
´
C.M
x
L/2
L/2
W
4
3W
4
boy man
and the distance of man from other end is
2
L
– x
3
L
6
L
2
L
=
-
=
44. (b,c)
45. (b) Position of C.M w.r. toA
A B C
1 0 1 AB 1 AC AB AC
1 1 1 3
´ + ´ + ´ +
= =
+ +
46. (b) Use theorem of parallel axes.
47. (a) Angular momentum
2
2 2
I MR .
5 T
p
= w =
2
4 MR
5T
p
=
48. (d)
2 1
2 1
t t
w -w
a =
-
1
2 1200
40
60
p´
w = = p ; 2
2 4500
150
60
p´
w = = p
2
110
rad /sec
10
p
a =
Now, radian 180
p = °
180
1 rad degree
=
p
2
11 180
degree/sec
p´
a =
p
= 1980 degree/sec2
49. (b) 2 2 2
I 2 5 (0.2) 2 2 (0.4) 1kg m
= ´ ´ + ´ ´ = ´
50. (b) E = 1500= 1/2× 1.2w2
2 3000
2500
1.2
w = =
50rad / sec
w =
50
t 2sec
25
w
= = =
a
51. (c) Velocity of P (NP) (NM MP)
= w = + w
r(r sin ) v(1 sin )
= + q w = + q
52. (d) Velocity at the bottom and top of the circle is 5gr
and gr . Therefore (1/2)M(5gr) = MgH and
(1/2) M (gr) = Mgh.
53. (a) Acceleration of a bodyrolling down an inclined plane
is given by , 2
2
gsin
a
K
1
R
q
=
+
In case of a solid sphere , we have
2 2
2 2 2 2
K [(I / M)] I (2 /5)MR 2
5
R R MR MR
= = = =
Substituting
2
2
K 2
5
R
= in equation (1) we get
5
a gsin
7
= q
54. (c) The velocity of the top point of the wheel is twice that
of centre of mass. And the speed of centre of mass is
same for both the wheels.
1
a
2
a
1
1 R
v w
=
1
R 2
2 R
v w
=
2
R
55. (c) 1
2
1
2
1
2
1
2
1
1 R
R
R
R
v
a w
=
w
=
=
2
2
2
2
2
2 R
R
v
a w
=
=
Taking particle masses equal
2
1
2
1
2
1
2
1
R
R
a
a
ma
ma
F
F
=
=
=
Alternative method : The force experienced by any
particle is onlyalong radial direction or the centripetal
force.
Force experienced bythe particle, F = mw2R
1 1
2 2
F R
F R
=
56. (d) t × Dt = L0 {Q since Lf = 0}
Þ t × Dt = Iw
or t× 60 = 2 × 2 × 60p/60
( f 60rpm
=
Q
60
2 f 2
60
ö
w = p = p´ ÷
ø
m
N
15
-
p
=
t
57. (c) m1d = m2 d2
2
1
2
m
d
m
d =
Þ
58. (d)
y1 y¢
1
Circular disc (1)
4
MR
I
2
1
y =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-209-320.jpg)





![NEWTON'S UNIVERSAL LAW OF GRAVITATION
Gravitational force is an attractive force between any two point
masses M1 and M2 separated by any distance r.
It is given by F = G 1 2
2
æ ö
ç ÷
è ø
M M
r
where G is the universal gravitational constant.
Its value, G = 6.67 × 10–11 Nm2 kg–2
Dimensions of G are [M–1 L3 T–2]
(a) The gravitational force is the central force and follows
inversesquare law. It acts along the linejoining theparticles.
(b) Since the work done by the gravitational force is
independent of the path followed and hence it is a
conservative force.
(c) It is the weakest force in nature. It is 1038 times smaller
than nuclear force and 1036 timessmaller than electricforce.
Strongest force being nuclear force (for small range)
followed by electric force.
(d) Gravitation is independent of the presence of other bodies
around it.
ACCELERATION DUE TO GRAVITY (g)
The force of attraction exerted by earth on a body of mass m is
the force of gravity.
So the force of gravityfrom Newton’s gravitational law is
2
= e
GM m
F
r
……(i)
where Me =mass of earth
r=distance of the body from the centre of earth.
The force of gravity can be written as F = mg ……(ii)
where g is called the acceleration due togravity.
From the expression (i) and (ii), we get
2
= e
GM
g
r
……(iii)
If body is located at the surface of earth i.e., r = Re (radius of
earth) then
3
2 2
(4 / 3 ) 4
3
p r
= = = pr
e e
e
e e
GM G R
g GR
R R
……(iv)
where r is the density of earth.
This is the relation between universal gravitational constant
'G' and acceleration due to gravity 'g'.
Change in the Value of Acceleration due to Gravity (g)
(i) Due to rotation or latitude of earth : Let us consider a
particle P at rest on the surface of earth at a latitude f.
( ) 2 2
cos
f = - w f
e
g g R
f
r
R g¢
w
At poles f= 90º, so g(f) = g ...(v)
At equator f = 0º so g(f) = g –w2Re ...(vi)
(ii) Due to shape of earth : The shape of the earth is not
perfectlyspherical. It is flattened at poles. The polar radius
is 21 km less than the equatorial radius. Hence acceleration
due to gravity at poles is greater than at the equator.
gp = 9.83 ms–2 = value of g at poles
ge = 9.78 ms–2 = values of g at equator
i.e. gp > ge
(iii) At a depth 'd' below the earth surface : The acceleration
due to gravity at the surface of earth.
G
R
3
4
R
GM
g e
2
e
e
ú
û
ù
ê
ë
é
r
p
÷
ø
ö
ç
è
æ
=
= (from eqn. iv) ...(vii)
d
R-d
O R
P
Earth
Surface of earth
8 Gravitation](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-215-320.jpg)
![212 PHYSICS
If a body is taken at a depth d belowthe earth surface, then
the body is attracted by inner core of mass M' of earth
radius (Re– d). Then acceleration due to gravityat point P
is
3
e
2 2
e e
G (4 /3) (R d)
GM
g
(R d) (R d)
é ù
p - r
¢ ë û
¢ = =
- -
( )
( )
r
-
p
= )
d
R
(
3
/
4
G e ...(viii)
From eqns. (vii) and (viii) we have
1
æ ö æ ö
-
¢ = = -
ç ÷ ç ÷
è ø è ø
e
e e
R d d
g g g
R R
...(ix)
The value of acceleration due to gravity at the centre of the
earth is zero.
(iv) At a height 'h' above the earth surface : The acceleration
due to gravity at the surface of earth from expression (iv)
is defined as
2
e
e
R
GM
g =
At a height h above the earth surface, the acceleration due
to gravity is
2
e
2
e
e
r
GM
)
h
R
(
GM
g =
+
=
¢ ...(x)
Þ
2
e
e
R
h
R
g
g
-
÷
÷
ø
ö
ç
ç
è
æ +
=
¢
Þ [from eqs.(ix) &(x)]
If h << Re
e
2
1
R
æ ö
» -
¢ ç ÷
è ø
h
g g ...(xi)
Keep in Memory
1. The value of the acceleration due to gravity on the moon
is about one sixth of that on the earth and on the sun is
about 27 times that on the earth.
E
s E M
g
g 27g and g
6
æ ö
= =
ç ÷
è ø
2. The value of g is minimum on the mercury, among all
planets.
3. For h<<R, the rate of decrease of the acceleration due to
gravitywith height istwice as compared tothat with depth.
4. The value of g increases with the increase in latitude. Its
value at latitude q is given by : gq= g – Rw2 cos2q.
5. Rotation of the earth about its own axis is responsible for
decrease in the value of g with latitude.
6. Theweight ofthebodyvaries along with the valueof g (i.e.
W = mg)
7. Inertial mass and gravitational mass-
(a) Inertial mass (Mi) defined byNewton's law of motion
Mi = F/a =
External force applied on the body
Acceleration produced in it
i 1 2
i 2 1
(M ) a
(M ) a
=
(ff applied force on (Mi)1 and (Mi)2 is same.)
(b) Gravitational mass Mg defined by Newton's law of
gravitation
Mg = gravity
to
due
on
Accelerati
body
of
Weight
g
W
g
Fg
=
=
8. If two spheres ofsame material, mass and radiusare put in
contact, the gravitational attraction between them isdirectly
proportional to the fourth power of the radius.
4
2
R
3
4
G
4
1
F ÷
ø
ö
ç
è
æ
ps
=
A
R
R
B
m 2R
¬ ® m
This system maybe considered to be made up of two mass
each separated by 2R distance.
9. If the earth stops rotating about its axis, the value of g at
the equator will increase by about 0.35%, but that at the
poles will remain unchanged.
If the earth starts rotating at the angular speed of about 17
times the present value, there will be weightlessness on
equator, but g at the poles will remain unchanged. In such a
case, the duration of the daywill be about 84 min.
10. If the radius of planet decreases by n%, keeping the mass
unchanged, the acceleration due to gravity on its surface
increases by 2n%. i.e.,
R
R
2
g
g D
-
=
D
11. If the mass of the planet increases by m% keeping the
radius constant, the acceleration due to gravity on its
surfaceincreases bym% i.e.,
g M
g M
D D
= where R= constant.
12. Ifthe densityof planet decreases by r % keeping the radius
constant, the acceleration due to gravitydecreases by r%.
13. If the radius of the planet decreases by r% keeping the
densityconstant, the acceleration due to gravitydecreases
by r%.
Example1.
What will be the acceleration due to gravity on the surface
of the moon with its radius as 1/4th the radius of the earth
and its mass as 1/80th the mass of earth?
Solution :
2
e
e
R
GM
g = and 2
m
m
R
GM
'
g = ;
5
1
1
4
80
1
R
R
M
M
g
'
g
2
2
m
e
e
m
=
÷
ø
ö
ç
è
æ
´
=
÷
÷
ø
ö
ç
ç
è
æ
= ; 5
/
g
'
g =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-216-320.jpg)
![213
Gravitation
Example2.
A mass M splits into two parts m and (M–m), which are
then separated by a certain distance. What will be the
ratio m/M which maximizes the gravitational force
between the two parts?
Solution :
2
x
)
m
M
(
Gm
F
-
= ;For maxima,
2
1
M
m
or
0
)
m
2
M
(
x
G
dm
dF
2
=
=
-
=
Example3.
Identical point masses each equal to m are placed at
x = 0, x = 1, x = 2, x = 4, ... The total gravitational force
on mass m at x = 0 due to all other masses is
(a) infinite (b) (4/3)Gm2
(c) (4/3GM2) (d) zero
Solution : (c)
o m m m
x=4
x=2
x=1
x=0
....
4
Gm
2
Gm
1
Gm
F
2
2
2
2
2
2
0 +
+
+
=
ú
û
ù
ê
ë
é
+
+
+
= ...
4
1
2
1
1
1
Gm
F
2
2
2
2
0
It is a G.P. with common ratio1/4.
ú
û
ù
ê
ë
é
-
=
4
/
1
1
1
Gm
F 2
0
3
Gm
4
F
2
0 =
Example4.
Four identical point masses each equal to m are placed
at the corners of a square of side a. The force on a point
mass m’ placed at the point of intersection of the two
diagonals is
(a) (4Gmm¢)/a2 (b) (2Gmm¢)/a2
(c) (Gmm¢)/a2 (d) zero
Solution : (d)
The forces acting on the mass m¢ placed at the point of
intersection of diagonals are balanced by each other as
shown in figure. Therefore net force is zero.
m m
m
m
m¢
F
F
F
F
Example5.
A tunnel is dug along the diameter of the earth. Determine
the force on a particle of mass m placed in the tunnel at a
distance x from the centre.
Solution :
Force on a mass m placed at a distance x from the centre is
equal to the force of gravity due to a mass of spherical
volume of earth of radius x.
m
R
x
Center of earth
2
3
x
m
d
3
x
4
G
F
÷
÷
ø
ö
ç
ç
è
æ p
=
where d = density of earth = 3
R
4
M
3
p
;
x
.
R
GMm
F
3
= [M is total mass of earth]
Example6.
If the radius of the earth were to shrink by two per cent,
its mass remaining the same, the acceleration due to
gravity on the earth’s surface would
(a) decrease by 2% (b) increase by 2%
(c) increase by 4% (d) decrease by 4%
Solution : (c)
As 2
R
GM
g = ; So, if R decreases then g increases.
Taking logarithm of both the sides;
log g = log G + log M – 2 log R
Differentiating it, we get
g
dg
= 0 + 0 –
R
dR
2
;
g
dg
100
4
100
2
2 =
÷
ø
ö
ç
è
æ -
-
=
% increase in 100
g
dg
g ´
= = %
4
100
100
4
=
´
Example7.
An apple of mass 0.25 kg falls from a tree. What is the
acceleration of the apple towards the earth? Also calculate
the acceleration of the earth towards the apple.
Given : Mass of earth = 5.983 × 1024 kg,
Radius of earth = 6.378 × 106 metre,
G = 6.67 × 10–11 Nm2kg–2.
Solution :
Mass of apple, m = 0.25 kg,
Mass of earth, M = 5.983 × 1024 kg,
Radius of earth, R= 6.378 × 106 metre
Gravitational constant, G = 6.67 × 10–11 Nm2kg–2
Let F be the gravitational force of attraction between the
apple and earth.
Then, 2
GmM
F
R
=
Let a be the acceleration of apple towards the earth.
2 2
F GmM GM
a
m mR R
= = =
Þ
11 24
2 2
6 2
6.67 10 5.983 10
a ms 9.810ms
(6.378 10 )
-
- -
´ ´ ´
= =
´](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-217-320.jpg)
![214 PHYSICS
Let a¢ be the acceleration of the earth towards the apple.
2
11
2
6 2
25 2
F Gm
a
M R
6.67 10 0.25
ms
(6.378 10 )
4.099 10 ms .
-
-
- -
= =
¢
´ ´
=
´
= ´
Example8.
The acceleration due to gravity at the moon’s surface is
1.67 ms–2. Iftheradius ofthemoon is 1.74× 106 m, calculate
the mass of the moon. Use the known value of G.
Solution :
2
GM
g
R
= or
2
gR
M
G
=
This relation is true not only for earth but for any heavenly
body which is assumed to be spherical.
Here,
2 6
g 1.67ms , R 1.74 10 m
-
= = ´ and
11 2 2
G 6.67 10 Nm kg
- -
= ´
Mass of moon,
6 2
22
11
1.67 (1.74 10 )
M kg 7.58 10 kg
6.67 10-
´ ´
= = ´
´
GRAVITATIONAL FIELD
(or Gravitational Field Intensity)
The region or space around a body in which its gravitational
influence is experienced by other bodies is the gravitational
field of that body.
The gravitational field strength Eg, produced by a mass M at
any point P is defined as the force exerted on the unit mass
placed at that point P. Then
2 2
æ ö
= = =
ç ÷
è ø
g
F G Mm GM
E m
m r r
...(i)
where m= test mass
r=distance between M and m
(i) The direction of Eg always points towards the mass
producing it.
(ii) The gravitational field can be represented bygravitational
lines of force.
(iii) The S.I unit of Eg is newton/kg. Its dimensions are
[M0LT–2].
Gravitational intensity (Eg) for spherical shell
r
|E |=0
g
Radius of
spherical shell
|E |
g
O
R
2
r
GM
|
Eg
| =
(i) |Eg|= 0 at points inside the spherical shell (i.e. r < R)
(ii) 2
| |
-
=
g
GM
E
R
at the surface of shell (i.e. r = R)
(iii) 2
| |
-
=
g
GM
E
r
for outside the spherical shell (r >R).
It is clear that as r increases, Eg decreases.
Gravitational intensity for solid sphere :
R
r
|E |
g
Solid
sphere
Eg
(i) 3
.
| |= -
g
GM r
E
R
for points inside the solid sphere (r<R)
(ii) At the surface of solid sphere (r = R) 2
| |= -
g
GM
E
R
(iii) Outside the solid sphere
2
| |= -
g
GM
E
r
(r > R)
GRAVITATIONAL POTENTIAL
Gravitational potential at any point is the work done by
gravitational force in carrying a body of unit mass from infinity
to that point in gravitational influence of source.
i.e., A
o
W GM
V
m r
-
= =
where r is the distance of point from source mass M.
The S.I. unit of V is joule/kg. Its dimensions are [M0L2T–2]. It is
a scalar quantity.
Gravitational potential at the earth surface is
-
= = -
e
A e
e
GM
V gR
R
Gravitational potential due to a uniform ring at a point on its
axis
2 2
= -
+
g
GM
V
a r
a
O r P
q
Gravitational potential due to a uniform thin spherical shell
O
Vg
r
R
GM
-](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-218-320.jpg)

![216 PHYSICS
1 Kg 1 Kg
1 Kg
1 Kg
1m
1m
1m 1m
2
m
2
m
When one mass is removed, then
P.E. = U2 = ú
û
ù
ê
ë
é ´
´
+
´
´
-
2
1
1
G
1
1
1
G
.
2
G
2
1
2
2
U2
ú
ú
û
ù
ê
ê
ë
é +
-
= ;
Work done =
ú
ú
û
ù
ê
ê
ë
é -
-
+
2
1
2
2
2
2
4
G =
ú
ú
û
ù
ê
ê
ë
é +
2
1
2
2
G
[Q Work done = change in P.E. = –U2–[–U1] = U1–U2]
Example10.
A solid sphere of uniform density and mass M has a radius
of 4m. Its centre is at the origin of coordinate system. Two
spheres of radii 1m are taken out so that their centres are
at P(0, –2, 0) and Q(0, 2, 0) respectively. This leaves two
spherical cavities. What is the gravitational field at the
centre of each cavity?
O
P Q
R
z
y
Solution :
If the cavities are not made, then the intensityat the point
P (or Q), due to whole sphere
32
GM
2
64
GM
x
.
R
GM
I 3
=
´
=
= where P Q R
I I I I
= + +
r r r r
Q
P
R I
I
I
I
r
r
r
r
-
-
= ……(i)
Where IR is the intensity of gravitational field at a point,
distance x from O due toremainder sphere (exclude cavity)
Mass of big sphere
3
d
)
4
(
4
M
3
´
p
=
Mass of small sphere P or Q,
3
4π (1)
3
´
=
d
m
M
m
64
=
At P, Ip = 0, ÷
ø
ö
ç
è
æ
=
=
64
M
.
4
G
r
Gm
I 2
2
Q
IR =
GM GM
32 1024
- [From eq (i)]
R
31GM
I
1024
=
Example11.
Find the gravitational potential energy of a system of four
particles, each having mass m, placed at the vertices of a
square of side l. Also obtain the gravitational potential at
the centre of the square.
Solution :
The system has four pairs with distance l and two diagonal
pairs with distance 2 l .
m
l
2l
m
m m
2 2 2 2
Gm Gm 2Gm 1 Gm
U 4 2 2 5.41
2 2
æ ö
= - - = - + = -
ç ÷
è ø
l l l
l
The gravitational potential at the centre of the square is
( )
r 2 / 2
= l
V = Algebraic sum of potential due to each particle
Þ
4 2Gm
V = -
l
Example12.
The radius of earth is R. Find the work done in raising a
body of mass m from the surface of earth to a height R/2.
Solution :
Ifa bodyofmass m is placed at a distance x from the centre
of earth, the gravitational force of attraction F between the
body and the earth is
2
x
m
GM
F =
Small amount of work done in raising a body through a
small distance dx is given by
dx
x
m
GM
dx
F
dW 2
=
=
Total work done in raising the body from the surface of
earth to a height R/2 is given by
W =
R R/2
2
R
GM m
dx
x
+
ò
=
3 R/2 3 R/2
2
R
R
1
GMm x dx GMm
x
- æ ö
= - ç ÷
è ø
ò
=
2 1
GMm
3R R
é ù
- -
ê ú
ë û
=
2
M m gR m
3R 3R
G
=
=
1
mg R
3
[ GM = gR2]](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-220-320.jpg)
![217
Gravitation
SATELLITES
A satellite is any body revolving around a large body under
the gravitational influence of the latter.
The period of motion T of an artificial satellite of earth at a
distance h above the surface of the earth is given by,
p
3
2
( + )
= 2 e
e
R h
T
gR
where, Re = radius of the earth
where, g = acceleration dueto gravityon thesurface ofthe earth.
If Re > > h, then e
R
T 2
g
= p ; Re = 6.4 × 106 m ;
g = 9.8 ms–2
i.e. T 84.58 minutes 5075sec
»
;
Assuming Re + h = r, the distance of the satellite from the centre
of the earth, 3 / 2
T (r)
µ
Orbital velocity (v0 )
Let a satellite ofmass m revolve around the earth in circular orbit
of radius r with speed v0. The gravitational pull between satellite
and earth provides the necessary centripetal force.
Centripetal force required for the motion =
2
0
mv
r
Gravitational force =
GMm
r²
2
0
2
mv GMm
r r
= or
2
0
GM
v
r
=
or 0 =
GM
v
r
..........(1)
or 0 =
+
g
v R
R h
[Q 2
GM
g
R
= and r = (R + h)]
Orbital velocity,
e
R
= =
e
e
GM
Vo gR
(i) Valueof orbital velocitydoes not depend on the mass of the
satellite.
(ii) Around the earth the value of orbital velocity is
7.92 km/sec.
(iii) Greater is the height of the satellite, smaller is the orbital
velocity.
(iv) The direction of orbital velocity is along the tangent to the
path.
(v) The work done by the satellite in a complete orbit is zero.
Angularmomentum (L):For satellite motion, angular momentum
will be given by
GM
L mvr mr
r
= = i.e., L = [m2GMr]1/2
Angular momentum of a satellite depends on both, the mass of
orbiting and central body. It also depends on the radius of the
orbit.
Energy of a satellite
Total energy of satellite revolving in an orbit of radius r around
the earth can be calculated as follows :
(i) The gravitational potential energy of a satellite of mass m
is –
=
g
GMm
U
r
, where r is the radius of the orbit.
(ii) Kinetic energy of the satellite is
2
0
1
2 2
= =
k
GMm
E mv
r
(iii) So, total energy of the satellite
2
= + = -
g k
GMm
E U E
r
The negative sign shows that satellite cannot leave the
orbit itself. It requires an energyequal to
2
GMm
R
, which is
called BindingEnergy (B.E.) ofsatellite.
(iv) Total energy of a satellite at a height equal to the radius of
the earth
1
– –
2( ) 4 4
= = =
+
GMm GMm
mgR
R R R
GEO-STATIONARY SATELLITE
A satelite which appears to be stationary for a person on the
surface of the earth is called geostationary satellite.
It is also known as parking satellite or synchronous satellite.
(i) The orbit ofthesatellitemust becircular and in theequatorial
plane of the earth.
(ii) The angular velocity of the satellite must be in the same
direction as the angular velocityof rotation ofthe earth i.e.,
from west to east.
(iii) The period ofrevolution ofthe satellite must be equal tothe
period of rotation of earth about its axis.
i.e. 24 hours = 24 × 60 × 60 = 86400 sec.
2 4 ²
T r³
GM
p
= or
1 1
2 2 2
3 3
2 2 2
GMT GM R T
r
4 R 4
æ ö æ ö
= = ´
ç ÷ ç ÷
p p
è ø è ø
=
1
3
6 2 (86400)²
9.8 (6.38 10 )
4 ²
é ù
´ ´ ´
ê ú
p
ë û
=42237 ×103 m = 42,237 km.»42000km.
h= r –R= 42000–6400= 35600km.
(a) Height of geostationary satellite from the surface of
the earth is nearly35600 km.
(b) The orbital velocity of this satellite is nearly
3.08km/sec.
(c) The relative velocity of geostationary satellite with
respect to earth is zero.
This type of satellite is used for communication
purposes. The orbit of a geostationary satellite is called
‘ParkingOrbit’.
Polar Satellite :
Polar satellites travel around the earth in an orbit that travels
around the earth over the poles. The earth rotates on its axis as
the satellite goes around the earth. Thus over a period of many
orbits it looks down on every part of the earth.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-221-320.jpg)
![218 PHYSICS
Different orbital shapes correspondingtodifferent velocitiesof
a satellite :
[1] When v< v0
(i) Thepath is spiral. The satellite finallyfalls on the earth
(ii) Kinetic energy is less then potential energy
(iii) Total energy is negative
[2] When v= v0
(i) The path is circular
(ii) Eccentricityis zero
(iii) Kinetic energy is less than potential energy
(iv) Total energy is negative
[3] When v0 < v< ve
(i) The path is elliptical
(ii) Eccentricity< 1
(iii) Kinetic energy is less than potential energy
(iv) Total energy is negative
[4] When v = ve
(i) The path is a parabola
(ii) Eccentricity= 1
(iii) Kinetic energy is equal to potential energy
(iv) Total energy is zero
[5] When v > ve
(i) The path is a hyperbola
(ii) Eccentricity> 1
(iii) Kinetic energy is greater than potential energy
(iv) Total energy is positive
If the orbit of a satellite is elliptical
(1) The energy
GMm
E
2a
= - = const. with ‘a’as semi-major axis;
(2) KE will bemaximum when the satelliteisclosestto thecentral
body(at perigee) and minimum when it is farthest from the
central body (at apogee) [as for a given orbit L = const.,
i.e., mvr = const., i.e., vµ 1/r]
(3) PE = (E – KE) will be minimum when KE = max, i.e., the
satellite is closest to the central body (at perigee) and
maximum when KE = min, i.e., the satellite is farthest from
the central body (at apogee).
ESCAPE SPEED (Ve)
It is the minimum speed with which a body should be projected
from the surface of a planet so as to reach at infinity i.e., beyond
the gravitational field of the planet.
If a bodyof mass m is projected with speed v from the surface of
a planet of mass M and radius R, then
as 2
1
2
=
K mv and
GMm
U
R
= - , ES = 2
1
2
mv –
GMm
R
Now if v' is the speed of body at ¥, then
2 2
1 1
( ) 0 ( )
2 2
¥ = + =
¢ ¢
E m v m v [as U 0
¥ = ]
So by conservation of energy
2 2
1 1
( )
2 2
= - = ¢
GMm
mv m v
R
i.e.
2 2
1
( )
2 2
1
= + ¢
GMm
mv m v
R
sov will be minimum when v¢ ® 0,
i.e. min
2
2
= = =
e
GM
v v gR
R 2
GM
as g
R
é ù
=
ê ú
ë û
• The value of escape velocitydoes not depend upon the mass
of the projected body, instead it depends on the mass and
radius of the planet from which it is being projected.
• The value of escape velocity does not depend on the angle
and direction of projection.
• The value of escape velocityfrom the surface of the earth is
11.2 km/sec.
• The minimum energyneeded for escape is = GMm/R.
• If the velocity of a satellite orbiting near the surface of the
earth is increased by 41.4%, then it will escape away from
the gravitational field of the earth.
• Ifa bodyfalls freelyfrom infinite distance, then it will reach
the surface ofearth with a velocityof 11.2 km/sec.
Relationbetweenorbital velocity(V0) andescape speed(Ve)
0
2 2
= =
e
V gR V
Keep in Memory
1. The escape velocity on moon is low
6
æ ö
=
ç ÷
è ø
E
m
g
as g hence
there is no atmosphere on moon.
2. If the orbital radius of the earth around the sun be one
fourth of the present value, then the duration of the year
will be one eighth of the present value.
3. The satellites revolve around the earth in a plane that
coincides with the great circle around the earth.
KEPLER'S LAWS OF PLANETARY MOTION
1. The law of orbits : Each planet revolves about the sun in
an elliptical orbit with the sun at one of the foci of the
ellipse.
ea
ea
P
x
Perihelion Aphelion
Sun
S¢
y
a a
S
a = Semi-major axis
A planet ofmass m moving in an elliptical orbit around the
sun. The sun of mass M, is at one focus S¢ of the ellipse.
The other focus is S, which is located in empty space. Each
focus is at distance ‘ea’ from the ellipse’s centre, with ‘e’
being the eccentricity of the ellipse and ‘a’ semimajor axis
of the ellipse, the perihelion (nearest to the sun) distance
rmin., and the aphelion (farthest from the sun) distance rmax.
are also shown.
rmax = a + e a = (1 + e) a
rmin = a – e a = (1 – e) a](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-222-320.jpg)







![227
Gravitation
49. A diametrical tunnel is dug across the Earth. A ball is
dropped into the tunnel from one side. The velocity of the
ball when it reaches the centre of the Earth is .... (Given :
gravitational potential at the centre of Earth =
R
GM
2
3
– )
(a) R (b) gR
(c) gR
5
.
2 (d) gR
1
.
7
50. A man of mass m starts falling towards a planet of mass M
and radius R.As he reaches near to the surface, he realizes
that he will pass through a small hole in the planet. As he
enters the hole, he seesthat the planet is reallymade of two
pieces a spherical shell ofnegligible thickness ofmass 2M/
3 and a point mass M/3 at the centre. Change in the force of
gravity experienced by the man is
(a) 2
2 GMm
3 R
(b) 0
(c) 2
1 GMm
3 R
(d) 2
4 GMm
3 R
51. In a region ofonlygravitational field ofmass 'M' a particle
is shifted from AtoB via three different paths in the figure.
The work done in different paths are W1, W2, W3
respectively then
M
B
A
3
2
1
C
(a) W1 = W2 = W3 (b) W1 > W2 > W3
(c) W1 = W2 > W3 (d) W1 < W2 < W3
52. Four similar particles of mass m are orbiting in a circle of
radiusr in thesameangular direction becauseoftheir mutual
gravitational attractiveforce. Velocityofa particle isgiven by
m
m
m
m r
(a)
1/ 2
GM 1 2 2
r 4
é ù
æ ö
+
ê ú
ç ÷
è ø
ê ú
ë û
(b) 3
GM
r
(c) ( )
GM
1 2 2
r
+ (d)
1/ 2
1 GM 1 2
2 r 2
é ù
æ ö
+
ê ú
ç ÷
è ø
ê ú
ë û
53. The percentage change in the acceleration of the earth
towards the sun from a total eclipse of the sun to the point
where the moon is on a side of earth directly opposite to
the sun is
(a)
s 2
m 1
M r
100
M r
´ (b)
2
s 2
m 1
M r
100
M r
æ ö
´
ç ÷
è ø
(c)
2
1 m
2 s
r M
2 100
r M
æ ö
´
ç ÷
è ø
(d)
2
s
1
2 m
M
r
100
r M
æ ö
´
ç ÷
è ø
54. A satellite is revolving round the earth in an orbit of radius
r with time period T. If the satellite is revolving round the
earth in an orbit ofradius r + Dr (Dr << r) with time periodT
+ D T then,
(a)
T 3 r
T 2 r
D D
= (b)
T 2 r
T 3 r
D D
=
(c)
T r
T r
D D
= (d)
T r
T r
D D
= -
55. A cavity of radius R/2 is made inside a solid sphere of
radius R. The centre ofthe cavity is located at a distance R/
2 from the centre of the sphere. The gravitational force on a
particle of mass ‘m’ at a distance R/2 from the centre of the
sphere on the line joining both the centres of sphere and
cavity is – (opposite to the centre of gravity)
[Here g = GM/R², where M is the mass of the sphere]
(a)
mg
2
(b)
3mg
8
(c)
mg
16
(d) None of these
56. A spherical uniform planet is rotating about its axis. The
velocityof a point on its equator is V. Due to the rotation of
planet about its axis the acceleration due to gravity g at
equator is 1/2 ofg at poles. The escape velocityof a particle
on the pole of planet in terms of V is
(a) Ve=2V (b) Ve=V
(c) Ve=V/2 (d) e
V 3V
=
57. The escape velocity from a planet is ve. A tunnel is dug
along a diameter of the planet and a small bodyis dropped
into it at the surface. When the body reaches the centre of
the planet, its speed will be
(a) ve (b) e
v / 2
(c) ve/2 (d) zero](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-231-320.jpg)

![230 PHYSICS
4. Satellites orbitting the earth have finite life and sometimes
debris of satellites fall to the earth. This is because
(a) the solar cells and batteries in satellites run out
(b) the laws of gravitation predict a trajectory spiralling
inwards
(c) of viscous forces causing the speed of satellite and
hence height to gradually decrease
(d) of collisions with other satellites
5. Both the earth and the moon are subject to the gravitational
force of the sun. As observed from the sun, the orbit of the
moon
(a) will be elliptical
(b) will not be strictly elliptical because the total
gravitational force on it is not central
(c) is not elliptical but will necessarily be a closed curve
(d) deviates considerably from being elliptical due to
influence of planets other than the earth
6. In our solar system, the inter-planetary region has chunks
ofmatter (much smaller in size compared toplanets) called
asteroids. They
(a) will not move around the sun, since they have very
small masses compared to the sun
(b) will move in an irregular way because of their small
masses and will drift away into outer space
(c) will move around the sun in closed orbits but not obey
Kepler's laws
(d) will move in orbits likeplanets and obeyKepler's laws
7. Choose the wrong option.
(a) Inertial mass is a measure of difficulty of accelerating
a bodyby an external force whereas the gravitational
mass is relevant in determining the gravitational force
on it byan external mass
(b) That thegravitational mass andinertial mass areequal
is an experimental result
(c) That the acceleration due togravityon the earth is the
samefor all bodies isduetotheequalityofgravitational
mass and inertial mass
(d) Gravitational mass of a particlelikeproton can depend
on the presence of neighbouring heavy objects but
the inertial mass cannot
8. Particles ofmasses 2M, mandM arerespectivelyat pointsA,
B and C with
1
( )
2
AB BC m
= × is much-much smaller than
M and at time t = 0, theyare all at rest as given in figure.
At subsequent times before any collision takes place.
r
A B C
M
m
2M
(a) m will remain at rest
(b) m will move towards M
(c) m will move towards2M
(d) m will have oscillatorymotion
NEET/AIPMT (2013-2017) Questions
9. Abody of mass ‘m’is taken from the earth’s surface to the
height equal to twice the radius (R) ofthe earth. The change
in potential energy of body will be [2013]
(a)
2
3
mgR (b) 3mgR
(c)
1
3
mgR (d) mg2R
10. Infinite number ofbodies, each of mass 2 kg are situated on
x-axisat distances1m,2m, 4m, 8m, .....respectively, from the
origin. The resulting gravitational potential due to this
system at the origin will be [2013]
(a)
8
3
- G (b)
4
3
- G
(c) – 4 G (d) –G
11. The radius of a planet is twice the radius of earth. Both
have almost equal average mass-densities. If VP and VE are
escape velocities of the planet and the earth, respectively,
then [NEET Kar. 2013]
(a) VE = 1.5VP (b) VP = 1.5VE
(c) VP = 2VE (d) VE = 3VP
12. A particle of mass ‘m’ is kept at rest at a height 3R from the
surface ofearth, where ‘R’ is radius of earth and ‘M’ is mass
of earth. The minimum speed with which it should be
projected, sothat it does not return back, is (g is acceleration
due to gravity on the surface of earth) [NEET Kar. 2013]
(a)
1
2
GM
R
æ ö
ç ÷
è ø
(b)
1
2
2
GM
R
æ ö
ç ÷
è ø
(c)
1
2
4
gR
æ ö
ç ÷
è ø
(d)
1
2
2
4
g
æ ö
ç ÷
è ø
13. Dependence of intensity of gravitational field (E) of earth
with distance(r) from centreofearth is correctlyrepresented
by: [2014]
(a)
E
O R
r
(b)
E
O
R r
(c)
E
O
R
r (d)
E
O
R r
14. A black hole is an object whose gravitational field is so
strong that even light cannot escape from it. To what
approximate radius would earth (mass = 5.98 × 1024 kg)
have to be compressed to be a black hole? [2014]
(a) 10– 9 m (b) 10– 6 m
(c) 10– 2 m (d) 100m](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-234-320.jpg)
![231
Gravitation
15. Twospherical bodies of mass M and 5 M and radii R and 2
Rreleased in free spacewith initial separation between their
centres equal to 12 R. If they attract each other due to
gravitational force only, then the distance covered by the
smaller bodybefore collision is [2015]
(a) 4.5R (b) 7.5R
(c) 1.5R (d) 2.5R
16. Kepler's third law states that square of period of revolution
(T)of a planet aroundthe sun, is proportional tothird power
of average distance r between sun and planet i.e. T2 = Kr3
here K is constant. If the masses of sun and planet are M
and m respectively then as per Newton's law ofgravitation
force of attraction between them is F = 2
GMm ,
r
here G is
gravitational constant. The relation between G and K is
described as [2015]
(a) GMK= 4p2 (b) K=G
(c) K =
1
G
(d) GK=4p2
17. A remote - sensing satellite of earth revolves in a circular
orbit at a height of0.25 × 106 m above the surface of earth.
If earth's radius is 6.38 × 106 m and g = 9.8 ms–2, then the
orbital speed of the satellite is: [2015 RS]
(a) 8.56 km s–1 (b) 9.13 km s–1
(c) 6.67 km s–1 (d) 7.76 km s–1
18. A satellite S ismovingin an elliptical orbit around theearth.
Themass ofthe satellite is verysmall compared to themass
of the earth. Then, [2015 RS]
(a) the total mechanical energy of S varies periodically
withtime.
(b) the linear momentum of S remains constant in
magnitude.
(c) the acceleration of S is always directed towards the
centre of the earth.
(d) the angular momentum of S about the centre of the
earth changes in direction, but its magnitude remains
constant.
19. The ratio of escape velocity at earth (ve) to the escape
velocityat a planet (vp) whoseradius and mean densityare
twice as that of earth is :
(a) 1: 2 (b) 1 : 2 2 [2016]
(c) 1: 4 (d) 1: 2
20. At what height from the surface of earth the gravitational
potential andthe value ofg are –5.4× 107 J kg–1 and 6.0 ms–2
respectively ?
Take the radius of earth as 6400 km : [2016]
(a) 2600km (b) 1600km
(c) 1400km (d) 2000km
21. Two astronauts are floating in gravitation free space after
having lost contact with their spaceship. The two will
(a) move towards each other. [2017]
(b) move away from each other.
(c) become stationary
(d) keep floating at the same distance between them.
22. The acceleration due to gravity at a height 1 km above the
earth is the same as at a depth d below the surface of earth.
Then [2017]
(a) d = 1 km (b) d =
3
km
2
(c) d = 2 km (d) d =
1
km
2](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-235-320.jpg)


![234 PHYSICS
9. (c) 2 3
T R
µ
Þ
3
2
1
2
2
1
R
R
T
T
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
Þ
2
/
3
2
/
3
2
1
2
1
4
1
R
R
T
T
÷
ø
ö
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
Þ 8
)
4
(
T
T 2
/
3
1
2
=
=
Þ 2 1
T 8 T 8 5 40
= ´ = ´ = hours
10. (b) At poles, the effect of rotation is zero and also the
distance from the centre of earth is least.
11. (c) 2 3
T R
µ (According to Kepler’s law)
2 13 3 2 12 3
1 2
T (10 ) and T (10 )
µ µ
2
3
1 1
2
2
2
T T
(10) or 10 10
T
T
= = .
12. (c) According to Kepler’s law of period T2 µ R3
2 3 3
1 1
2 3 3
2 2
(6 )
8
(3 )
T R R
T R R
= = =
2
2
24 24
8
T
´
=
2
2
24 24
8
T
´
= = 72=36 ×2
2 6 2
T =
13. (b) Since escape velocity( )
e e
v 2gR
= is independent
of angle of projection, so it will not change.
14. (c) Given that l2 = 1.02 l1
We know that T 2π or T
g
æ ö
= µ
ç ÷
è ø
l
l
2 2 1
1 1 1
T (1.02 )
101
T
æ ö
= = =
ç ÷
è ø
l l
l l
Thus time period increases by 1%.
15. (b) We know that e 0
v 2 v
= , where v0 is orbital
velocity.
K.E. in the orbit,
2
0
1
E M v
2
=
K.E. to escape
2 2
e 0
1 1
E M v M (2 v )
2 2
= =
2
0
1
M v 2 2E
2
= ´ =
16. (c)
1/ 2
3
2π (R h)
T
R g
é ù
+
= ê ú
ê ú
ë û
Here (R + h) changes from R to 4 R. Hence period of
revolution changes from T to (43)1/2 T = 8 T.
17. (b) h
2h
g g 1
R
æ ö
= -
ç ÷
è ø
x
x
g g 1
R
æ ö
= -
ç ÷
è ø
Given that, h x
g g
=
x= 2h
18. (d) 2
2
)
x
R
(
GmM
)
x
R
(
mv
+
=
+ also 2
R
GM
g =
2 2
2 2
mv GM R
m
(R x) R (R x)
æ ö
= ç ÷
è ø
+ +
2
2
2
)
x
R
(
R
mg
)
x
R
(
mv
+
=
+
x
R
gR
v
2
2
+
=
Þ
2
/
1
2
x
R
gR
v
÷
÷
ø
ö
ç
ç
è
æ
+
=
19. (c) 2
2
)
x
R
(
GmM
x
R
mv
+
=
+
x = height ofsatellite from earth surface
m = mass of satellite
2 GM GM
v or v
(R x) R x
Þ = =
+ +
2 (R x) 2 (R x)
T
v GM
R x
p + p +
= =
+
which is independent of mass of satellite
20. (c) 2
n
MR
KR
F w
=
= - )
1
n
(
2
KR +
-
=
w
Þ
or 2
)
1
n
(
R
'
K
+
-
=
w [where K' = K1/2, a constant]
2
)
1
n
(
R
T
2
+
-
a
p
(n 1)
2
T R
+
a
21. (d) According to Newton gravitational force
mg
R
m
GM
2
e
e
= & g
m
)
h
R
(
m
GM
2
e
e ¢
=
+
Þ g'
2
e
2
e
2
e )
h
R
(
gR
)
R
/
h
1
(
1
g
+
=
+
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-238-320.jpg)
![235
Gravitation
where Me is mass ofearth, G is gravitational constant,
Re is radius & earth, h is height of satellite above the
surfaceof earth, g is value at the surface of earth, g' is
value at height h above the surface of earth.
so g
m
)
h
R
(
mgR
)
h
R
(
mv
2
e
2
e
e
2
¢
=
+
=
+ h
R
gR
v
e
2
e
+
=
Þ
h
Re
+Re
O
Earth
earth
surface
satellite
orbit
v
22. (c)
23. (d) Both decreases but variation are different.
24. (b) There is no gravitational field in the shell.
25. (c) Thegravitational field duetothe ring at a distance r
3
is given by
2
2
/
3
2
2
r
8
Gm
3
E
]
)
r
3
(
r
[
)
r
3
(
Gm
E =
Þ
+
=
Attractive force = 2
r
8
GmM
3
26. (a) For uniform gravitational field
Eg =
r
V
-
2
ms
10
1
20
2 -
=
-
-
=
Now, W = mgh =
1
5 4 2J
10
´ ´ =
27. (b)
2
0
2
2
e
1 mv
2
1
E
,
mv
2
1
E =
=
0
e
2
0
e
2
1
v
2
v
2
v
v
E
E
=
=
÷
÷
ø
ö
ç
ç
è
æ
=
Q
28. (d) g R
µ r
29. (c)
30. (b) As buoyant force involves ‘g’ in it.
31. (d) Work done = Uf – Ui
mgR
3
2
R
GmM
3
2
R
Gmm
R
R
2
GMm
=
=
÷
ø
ö
ç
è
æ
-
-
+
-
=
32. (b) 33. (a)
34. (d) The gravitational force due to the whole sphere at A
point is
e o
1 2
GM m
F
(2R)
= , where m0 is the assumed rest mass at
point A.
In the second case, when we made a cavity of radius
(R/2), then gravitational force at point Ais
2
o
e
2
)
2
/
R
R
(
m
GM
F
+
= F2/F1= 1/9
35. (b)
R
2
R0 0
GMm 1 1
P.E. dr GMm
R R
r
é ù
= = - -
ê ú
ë û
ò
TheK.E. acquired bythe bodyat the surface
2
1
m v
2
=
2
0
1 1 1
mv GMm
2 R R
é ù
= - -
ê ú
ë û
0
1 1
v 2G M
R R
æ ö
= -
ç ÷
è ø
36. (c) Applying the properties of ellipse, we have
1 2
1 2 1 2
r r
2 1 1
R r r r r
+
= + =
R
Instant position
of satellite
major axis
r2
r1
Sun
1 2
1 2
2r r
R
r r
=
+
37. (a)
GM
v
r
æ ö
= ç ÷
è ø
where r is radius of the orbit of the
satellite.
herer =Re + h = e
e e
R 3
R R
2 2
+ =
So, 0
e
2GM 2
v v
3R 3
= = ,
where v0 is the orbital velocity of the satellite, which
is moving in circular orbit of radius, r = Re
38. (d) 2 2
1 1 2 2 1 1 2 2
v r v r or r ω r ω
= =
(QL=mrv= constant)
or 2 2
min max
r ω r ω¢
=
2 2
min max
ω (r / r )ω
¢
=
39. (c) Distance between the surface of the spherical bodies
= 12R – R– 2R = 9R
Force Mass
µ
Acceleration Mass
µ
Distance Acceleration
µ
Þ 1
2
a M 1
a 5M 5
= = Þ 1
2
2
1
S
5
S
5
1
S
S
=
Þ
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-239-320.jpg)
![236 PHYSICS
S1 + S2 = 9
Þ 6S1 = 9Þ 5
.
1
6
9
S1 =
=
S2 = 1.5×5 = 7.5
Note: Maximum distance will be travelled bysmaller
bodies due to the greater acceleration caused by the
same gravitational force
40. (c) 2
2
)
R
99
.
0
(
GM
'
g
;
R
GM
g =
=
2
2
g' R
g' g
g 0.99R
æ ö
= Þ >
ç ÷
è ø
41. (b) Acceleration due to gravity at lattitude’ l ’ is given by
l
w
-
=
l
2
2
e
e cos
R
g
g
At equator, l = 90° Þ l
cos = cos 90° = 0
or l
g = e
g = g (as given in question)
At 30°,
2
2
2
30 R
4
3
g
30
cos
R
g
g w
-
=
w
-
=
or, 2
30 R
4
3
g
g w
=
-
42. (b) The orbital speed of satellite is independent of mass
of satellite, so ball will behave as a satellite & will
continue to move with same speed in original orbit.
43. (a) The total momentum will be zero and hence velocity
will be zero just after collisiion. The pull of earth will
makeit fall down.
44. (d) Weight of liquid displaced = mg.
45. (a) The force of attraction between sphere and shaded
position
2
x
l
÷
ø
ö
ç
è
æ
=
dx
m
GM
dF
x
r l
m
M
r + l
2 2
2 1
2
1
1
2 1
1
( )
+ +
+
+ - +
-
+
+
-
= =
é ù
= = ê ú
- +
ë û
é ù
é ù
= - = - =
ë û ê ú +
ë û
ò ò
ò
r l r l
r r
r l
r l
r r
r l
r l
r
r
GMm GMm
F dx dx
lx l x
GMm GMm x
x dx
l l
GMm GMm GMm
x
l l x r r l
46. (a)
2 4 3
1 since
2
æ ö æ ö
= - = = +
ç ÷ ç ÷
è ø è ø
h g R
g g h R
h R h
Force on the satellite = mg
9
4
mgh =
N
889
10
200
9
4
»
´
´
=
47. (c)
2
R
1
g µ so we will not get a straight line.
AlsoF = 0 at a point where Force due to Earth = Force
due to mars
48. (c) Applying conservation of energy principle, we get
r
GMm
R
GMm
v
mk
2
1 2
e
2
-
=
-
r
GMm
R
GMm
R
GM
2
mk
2
1 2
-
=
-
Þ
R
k
R
1
r
1
r
1
R
1
R
k 2
2
-
=
Þ
-
=
-
Þ
2
2
k
1
R
r
)
k
1
(
R
1
r
1
-
=
Þ
-
=
Þ
49. (b) Loss in potential energy= Gain in kineticenergy
2
mv
2
1
R
GMm
2
3
R
GMm
=
÷
ø
ö
ç
è
æ
-
-
-
gR
R
GM
v
mv
2
1
R
2
GMm 2
=
=
Þ
=
Þ
50. (a) Change in force of gravity
=
2 2
M
G m
GMm 3
R R
- (onlydue tomass M/3 due toshell
gravitational field is zero(inside the shell))
= 2
2GMm
3R
51. (a)
52. (a) Centripetal force = net gravitational force
2
0
1
mv
2Fcos45 F
r
= ° + =
2 2
2 2
2GM 1 Gm
2
( 2r) 4r
+
r
V0
F F
F1
2r
45°
2 2
0
2
mv Gm
[2 2 1]
r 4r
= +
1/2
GM(2 2 1
4r
æ ö
+
Þ ç ÷
è ø](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-240-320.jpg)
![237
Gravitation
53. (c) During total eclipse :
Total attraction due to sun and moon,
s e m e
1 2 2
1 2
GM M GM M
F
r r
= +
When moon goes on the opposite side of earth.
Effective force of attraction,
s e m e
2 2 2
1 2
GM M GM M
F
r r
= -
Change in force,
m e
1 2 2
2
2GM M
F F F
r
D = - =
Change in acceleration ofearth
Da =
m
2
e 2
2GM
F
M r
D
=
Average force on earth, Fav =
av s
2
e 1
F GM
M r
=
%age change in acceleration
=
2
m 1
2
av s
2
2GM r
a
100 100
a GM
r
D
´ = ´ ´
2
1 m
2 s
r M
2 100
r M
æ ö
= ´
ç ÷
è ø
54. (a) Since, 3
2
kr
T =
Differentiating the above equation
Þ
T r
2 3
T r
D D
= Þ
T 3 r
T 2 r
D D
=
55. (b) Gravitational field at mass m due to full solid sphere
1 0
0 0
r R 1
E ........
3 6 4 G
r r é ù
= = e =
ê ú
e e p
ë û
r
r
Gravitational field at mass m due to cavity(–r)
3 3
2 2 2
0 0
( ) (R / 2) r a
E ........ using E
3 R 3 r
é ù
-r r
= =
ê ú
e e
ê ú
ë û
r
r
=
3
2
0
0
( )R R
24
24 R
-r -r
- = -
e
e
R
m
R/2
CM
Net gravitational field
1 2
0 0
R R
E E E
6 24
r r
= + = -
e e
r r r
0
R
8
r
=
e
Net force on m
0
m R
F mE
8
r
® = =
e
r
Here, 0
3
M 1
&
4 G
(4 /3) R
r = e =
p
p
then
3mg
F
8
=
56. (a) V= wR
2
0
g g R
= - w [g = at equator, g0 = at poles]
2
0
0
g
g R
2
= - w ;
2 0
g
R
2
w = ;
2 0
g R
V
2
=
2
e 0
V 2g R 4V 2V
= = =
57. (b)
2
e
1 GMm
mv
2 R
= ; e
GMm
v 2gR
R
= =
In tunnel bodywill perform SHM at centre
Vmax = Aw (see chapter on SHM)
=
e
v
R2
gR
2 R / g 2
p
= =
p
58. (b) 2
1
g
R
µ
R decreasing g increase hence, curve b represents
correct variation.
59. (a) Here,
2GM
v
R
= and
2GM
kv
R R
=
+
.
Solving
1
k
2
=
60. (b) Potential energy of particle at the centre of square
GMm
4
a
2
æ ö
ç ÷
= - ç ÷
ç ÷
è ø
2 2
GMm 1 8 2 GM
4 mv 0 v
a 2 a
2
æ ö
ç ÷
- + = Þ =
ç ÷
è ø
61. (b) T2 a r3, where r = mean radius =
2
r
r 2
1 +
62. (d) ÷
ø
ö
ç
è
æ
-
-
+
-
=
-
=
D
R
GMm
h
nR
GMm
U
U
U i
f
mgR
1
n
n
R
GMm
.
1
n
n
+
=
+
=
63. (c)
GM
)
h
R
(
2
T
3
+
p
=
GM
)
R
01
.
1
(
2
T
,
GM
R
2
T
3
2
3
1 p
=
p
=
%
5
.
1
100
T
T
T
1
1
2
=
´
-
64. (b) Electronic charge does not depend on acceleration
due to gravity as it is a universal constant.
So, electronic charge on earth
= electronic charge on moon
Required ratio = 1.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-241-320.jpg)

![239
Gravitation
6. (d) Asteroids are also being acted upon by central
gravitational forces, hence Asteroid will move in
circular orbits like planets and obey Kepler's laws.
7. (d) Gravitational mass of proton is equivalent to its inertial
mass and is independent of presence of neighbouring
heavy objects so verifies the option (d).
8. (c) Force of Gravitation,
2
g
GMm
F
r
=
Let AB = r
So, force on B due to A
2
(2 )
( )
BA
G Mm
F
AB
= = towards BA.
2
(2 )
2 g
G Mm
F
r
= =
and force on B due to C
2
( )
BC
GMm
F
BC
= = towards BC
As, (BC) = 2AB
2 2 2
4
(2 ) 4( ) 4
g
BC
F
GMm GMm GMm
F
AB AB r
Þ = = = =
As FBA > FBC,
hence, m will move towards (BA) i.e., (2M).
NEET/AIPMT (2013-2017) Questions
9. (a) Initial P
.E.,Ui =
GMm
R
-
,
Final P.E., Uf =
GMm
3R
-
[QR' = R+ 2R= 3R]
Change in potential energy,
DU=
GMm
3R
-
+
GMm
R
=
GMm
R
1
1
3
æ ö
-
ç ÷
è ø
=
2
3
GMm
R
=
2
3
mgR
GMm
mgR
R
æ ö
=
ç ÷
è ø
Q
ALTERNATE:DU=
mgh
h
1
R
+
By placing the value of h = 2R we get
DU=
2
3
mgR.
10. (c)
m
Gravitational potential V=
Gm
r
-
V0 = –
G 2
1
´
–
G 2
2
´
–
G 2
4
´
–
G 2
8
´
– 2G
1 1 1
1 ....
2 4 8
é ù
+ + + + ¥
ê ú
ë û
= – 2G ×
1
1
1
2
-
= – 2G ×
1
1
2
= – 4 G.
.
11. (c) Escape velocity,
8
3
e
V R GP
= p
Þ Ve µ R Þ 2
P P
E E
V R
V R
= =
Þ VP = 2VE.
12. (b) As we know, the minimum speed with which a bodyis
projected so that it does not return back is called
escape speed.
2 2 2
4
= = =
+
e
GM GM GM
V
r R h R
1
2
( 3 )
2
æ ö
= =
ç ÷
è ø
Q
GM
h R
R
13. (b) First when (r < R) E µ r and then when r > R
2
1
E
r
µ .
Hence graph (b) correctly dipicts.
14. (c) From question,
Escape velocity
=
2GM
R
= c = speed of light
Þ R=
2
2GM
c
=
11 24
8 2
2 6.6 10 5.98 10
m
(3 10 )
-
´ ´ ´ ´
´
= 10– 2 m
15. (b)
12R–3R=9R
12R
M
R 2R
5M
Before collision
M
5M
R 2R
At the time of collision
Let the distance moved by spherical body of mass M
is x1 and by spherical body of mass 5m is x2
As their C.M. will remain stationary
So, (M) (x1) = (5M)(x2)or, x1 =5x2
and for tauching x1 + x2 = 9R
So, x1 =7.5R
16. (a) As we know, orbital speed, orb
GM
V
r
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-243-320.jpg)


![242 PHYSICS
Its S.I. Unit is Nm-2
Stress is a tensor as its value changes when direction changes.
Types of Stress :
Longitudinal stress or tensile stress, volumetric stress and
tangential stress are the types of stress.
Strain :
It is defined as the ratio of the change in shape or size to the
original shape or size of the body.
=
Change in dimension
Strain
Original dimension
Strain has no units or dimensions.
Types of Strain :
Longitudinal strain : It is defined as the ratio of the change in
length to the original length.
Longitudinal strain =
Dl
l
Volume strain : It is the ratio of the change in volume to the
original volume.
Volume strain =
DV
V
Shearing strain : It is the angular deformation produced in a
body.
Shearing strain (q) =
Dx
h
HOOKE’S LAW
It is the fundamental law of elasticity given byRobert Hooke in
1679. It states that “the stress is directly proportional to strain
provided the strain is small “.
i.e. Stress µ strain constant
Þ = =
stress
E
strain
This proportionality constant is called modulus of elasticity
(name given byThomasYoung) or coefficient of elasticity (E).
Since stress has same dimensions as that of pressure and strain
is dimensionless. So the dimensions of E is same as, that of
stress or pressure i.e. [ML–1T–2]
The modulus of elasticity depends on the material and on the
nature of deformation. There are three type of deformations and
therefore three types of modulus of elasticity.
(i) Young’s modulus (Y) : It measuresthe resistance ofa solid
to elongation.
(ii) Shear modulus )
(h or modulus of rigidity : It measures
the resistance to motion of the plane of a solid sliding part
on each other.
(iii) Bulk modulus (B) : It measure the resistance that solid or
liquid offer to their volume change.
The stress under which the system breaks is called breaking
stress.
(i) Young's modulus (Y) : Let us consider a long bar (shown
in fig.) of cross-sectional area A and length lo, which is
clamped at one end. When we apply external force Fl
longitudinally along the bar, internal forces in bar resist
distortion, but bar attains equilibrium in which its length is
greater and in which external force is exactlybalanced by
internal forces. The bar is said to be stressed in this
condition.
l0
Fl
Fixed
Dl
Now if the solid bar obey the Hooke’ law, the Young's
modulus, Y is defined as
Tensile stress
= =
D
l
l l
/
/
F A
Y
Tensile strain
Where Dl is change in the length of bar, when we
apply Fl.
(ii) Shear modulus (h) : Shear modulus or modulus of
rigidityh is
h = =
D
/
/
t
F A
Shearing stress
Shearing strain x h
Ft
h
Dx
q
Fixed face
(a) As we see, there is no change in volume under
this deformation, but shape changes.
(b ) q
»
q
=
D
tan
h
x
(see the figure), where q is shear
angle.
(iii) Bulk modulus (B) : The Bulk modulus B is defined
as
-D
= = =
D D
/
/ /
n
F A
Volume stress P
B
Volume stain V V V V
Fn
V
V– V
D
Negative sign comes to make B positive, because with the
increase of pressure, the volume of body decreases or vice
versa.
The reciprocal of the Bulk modulus is called
compressibility of material
i.e., Compressibility = 1/B.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-246-320.jpg)





![248 PHYSICS
15. A and B are two wires. The radius of A is twice that of B.
They are stretched by the same load. Then the stress on B
is
(a) equal to that on A (b) four times that on A
(c) two times that on A (d) half that on A
16. Hooke's law defines
(a) stress
(b) strain
(c) modulus of elasticity
(d) elasticlimit
17. In case of steel wire (or a metal wire), the limit is reached
when
(a) the wire just break
(b) the load is more than the weight of wire
(c) elongation is inversely proportional to the tension
(d) None of these
18. A steel ring of radius r and cross sectional area A is fitted
onto a wooden disc of radius R (R > r). If the Young’s
modulus of steel is Y, then the force with which the steel
ring is expanded is
(a) AY(R/r) (b) AY(R – r)/r
(c) (Y/A)[(R– r)/r] (d) Yr/A R
19. Which of the following relation is true ?
(a) 3 (1 )
Y K
= - s (b)
9 Y
K
Y
h
=
+ h
(c) (6 )
K Y
s = + h (d)
05.Y - h
s =
h
20. For a constant hydraulic stress on an object, the fractional
change in the object volume
V
V
D
æ ö
ç ÷
è ø
and its bulk modulus
(B) are related as
(a)
V
B
V
D
µ (b)
1
V
V B
D
µ
(c)
2
V
B
V
D
µ (d)
2
V
B
V
-
D
µ
21. The diagram shown below represents the applied forces
per unit area with the corresponding change X (per unit
length) produced in a thin wire of uniform cross section in
the curve shown. Theregion inwhich the wirebehaveslikea
liquidis
(a) ab
(b) bc
(c) cd
F
O X
a
b
c
d
(d) Oa
22. A steel wire is suspended vertically from a rigid support.
When loaded with a weight in air, it extends byla and when
theweight is immersed completelyin water, the extension is
reduced to lw. Then the relative density of material of the
weight is
(a) w
a / l
l (b)
w
a
a
l
l
l
-
(c) )
/( w
a
w l
l
l - (d) a
w / l
l
23. When an elastic material with Young’s modulus Y is
subjected to stretching stress S, elastic energy stored per
unit volumeof the material is
(a) YS/ 2 (b) S2Y/ 2
(c) S2 /2Y (d) S/ 2Y
24. The ratio of shearing stress to the corresponding
shearing strain is called
(a) bulk modulus (b) Young's modulus
(c) modulus of rigidity (d) None of these
25. The Young’s modulus of a perfectly rigid body is
(a) unity
(b) zero
(c) infinity
(d) some finite non-zero constant
1. Two wires of same material and length but cross-sections
in the ratio 1 : 2 are used to suspend the same loads. The
extensions in them will be in the ratio
(a) 1: 2 (b) 2: 1
(c) 4: 1 (d) 1: 4
2. Abodyof mass 10 kg is attached to a wire ofradius 3cm. It’s
breakingstressis4.8× 107 Nm–2, thearea ofcross-section of
thewireis10–6 m2.Whatisthemaximumangularvelocitywith
which it can be rotated in the horizontal circle?
(a) 1 rad sec–1 (b) 2 rad sec–1
(c) 4 rad sec–1 (d) 8 rad sec–1
3. The Young’s modulus of brass and steel are respectively
1010 N/m2. and2 × 1010 N/m2.Abrass wire and a steel wire
of the same length are extended by 1 mm under the same
force, the radii of brass and steel wires are RB and RS
respectively. Then
(a) B
S R
2
R = (b) 2
/
R
R B
S =
(c) B
S R
4
R = (d) 4
/
R
R B
S =
4. A steel wire of length 20 cm and uniform cross-section
1 mm2 is tied rigidly at both the ends. The temperature of
the wire is altered from 40ºC to 20ºC. Coefficient of linear
expansion for steel a = 1.1 × 10–5/ºC and Y for steel is
2.0 × 1011 N/m2. The change in tension of the wire is
(a) 2.2 × 106 newton (b) 16 newton
(c) 8 newton (d) 44 newton](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-252-320.jpg)



![252 PHYSICS
Exemplar Questions
1. Modulus of rigidityof ideal liquids is
(a) infinity
(b) zero
(c) unity
(d) some finite small non-zero constant value
2. The maximum load a wire can withstand without breaking,
when its length is reduced to half of its original length, will
(a) be double (b) be half
(c) be four times (d) remain same
3. The temperature of a wire is doubled. TheYoung's modulus
of elasticity
(a) will also double (b) will become four times
(c) will remain same (d) will decrease
4. A spring is stretched byapplying a load to its free end. The
strain produced in the spring is
(a) volumetric
(b) shear
(c) longitudinal and shear
(d) longitudinal
5. A rigid bar of mass M is supported symmetrically bythree
wires each of length l. Those at each end are of copper and
themiddle one is ofiron. The ratiooftheir diameters, ifeach
is to have the same tension, is equal to
(a) Ycopper / Yiron (b)
iron
copper
Y
Y
(c)
2
iron
2
copper
Y
Y
(d)
iron
copper
Y
Y
6. A mild steel wire of length 2L and cross-sectional area A is
stretched, well within elastic limit, horizontallybetween two
pillars (figure ). Amass m is suspended from the mid-point
ofthe wire. Strain in the wire is
m
x
2L
(a)
2
2
2
x
L
(b)
x
L
(c)
2
x
L
(d)
2
2
x
L
7. A rectangular frame is to be suspended symmetrically by
two strings ofequal length on two supports (figure). It can
be done in one of the following three ways;
(a) (b) (c)
The tension in the strings will be
(a) the same in all cases (b) least in (a)
(c) least in (b) (d) least in (c)
8. Consider two cylindrical rods of identical dimensions, one
of rubber and the other of steel. Both the rods are fixed
rigidlyat one end to the roof. A mass M is attached to each
of the free ends at the centre of the rods.
(a) Both the rods will elongate but there shall be no
perceptible change in shape
(b) The steel rod will elongate and change shape but the
rubber rod will onlyelongate
(c) The steel rod will elongate without any perceptible
change in shape, but the rubber rod will elongate and
the shape of the bottom edge will change to an ellipse
(d) The steel rod will elongate, without any perceptible
changein shape, but the rubber rod will elongate with
the shape of the bottom edge tapered to a tip at the
centre
NEET/AIPMT (2013-2017) Questions
9. The following four wires are made of the same material.
Which of these will have the largest extension when the
same tension is applied ? [2013]
(a) Length = 100 cm, diameter = 1mm
(b) Length = 200 cm, diameter = 2 mm
(c) Length = 300 cm, diameter = 3 mm
(d) Length = 50cm, diameter = 0.5mm](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-256-320.jpg)
![253
Mechanical Properties of Solids
10. If the ratio of diameters, lengths and Young’s modulus of
steel and copper wires shown in the figure are p, q and s
respectively, then the corresponding ratio of increase in
their lengths would be [NEET Kar. 2013]
(a)
7
(5 )
q
sp
(b) 2
5
(7 )
q
sp
Steel
2m
Copper
5m
(c) 2
7
(5 )
q
sp
(d)
2
(5 )
q
sp
11. Copper of fixed volume ‘V; is drawn into wire of length ‘l’.
When this wire is subjected to a constant force ‘F’, the
extension produced in the wire is ‘Dl’. Which of the
following graphs is a straight line? [2014]
(a) Dl versus
1
l
(b) Dl versus l2
(c) Dl versus 2
1
l
(d) Dl versus l
12. The approximate depth of an ocean is 2700 m. The
compressibilityof water is 45.4 × 10–11 Pa–1 and densityof
water is 103 kg/m3.What fractional compression of water
will be obtained at the bottom of the ocean ? [2015]
(a) 1.0 × 10–2 (b) 1.2 × 10–2
(c) 1.4 × 10–2 (d) 0.8 × 10–2
13. The Young's modulus of steel is twice that of brass. Two
wires of same length and of same area of cross section, one
of steel and another of brass are suspended from the same
roof. If we want the lower ends of the wires to be at the
same level, then the weights added to the steel and brass
wires must be in the ratio of : [2015 RS]
(a) 2 :1 (b) 4 : 1
(c) 1 :1 (d) 1 : 2
14. Thebulkmodulus ofa sphericalobject is'B'. Ifit is subjected
to uniform pressure 'p', the fractional decrease in radius is
(a)
B
3p
(b)
3p
B
[2017]
(c)
p
3B
(d)
p
B](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-257-320.jpg)
![254 PHYSICS
EXERCISE - 1
1. (c) 2. (b) 3. (d) 4. (a) 5. (d)
6. (c) 7. (a)
8. (c) Couple per unit angle of twist,
l
2
r
C
4
h
p
=
Couple t =
l
2
r
C
4
q
h
p
=
q
Here h, l, C & t are same. So, r4q = constant
÷
÷
ø
ö
ç
ç
è
æ
=
q
q
4
1
4
2
2
1
r
r
9. (a)
strain
stress
)
90
tan( =
q
-
10. (c) If l isthe original length ofwire, then changein length
offirst wire, )
( 1
1 l
l
l -
=
D
change in length of second wire, )
( 2
2 l
l
l -
=
D
Now,
2
2
1
1
A
T
A
T
Y
l
l
l
l
D
´
=
D
´
=
or
2
2
1
1 T
T
l
l D
=
D
or
l
l
l
l -
=
- 2
2
1
1 T
T
or T1 l 2 – T1 l = T2 l 1 – l T2 or
1
2
2
1
1
2
T
T
T
T
-
-
=
l
l
l
11. (c) F F mg
Y
A YA YA
= Þ D = =
D
l l l
l
l
12. (d) The elasticity of a material depends upon the
temperature of the material. Hammering & annealing
reduces elastic property of a substance.
13. (b) The ratio of stress to strain is always constant. If
stress is increased, strain will also increase so that
their ratio remains constant.
14. (c)
1
FL
l l
YA A
= Þ µ
15. (b) Stress = 2
Force 1
Stress
Area πr
µ
2
2
(2) 4
B A
B A
A B
S r
S S
S r
æ ö
= = Þ =
ç ÷
è ø
16. (c)
17. (d) According to Hooke's Law, within the elastic limits
stress is directly proportional to strain.
18. (b) Let T be the tension in the ring, then
)
r
R
(
A
r
T
)
r
R
(
2
.
A
r
2
.
T
Y
-
=
-
p
p
=
r
)
r
R
(
A
Y
T
-
=
19. (d)
0.5
2 (1 )
Y
Y
- h
= h + s Þ s =
h
20. (b)
1
/
p V
B
V V B V
D D
= Þ µ
D
[Dp = constant]
21. (b) The wire starts behaving like a liquid at point b. It
behaves like a viscous liquid in the region bc of the
graph.
22. (b) Let V be the volume of the load and r its relative
density
So,
a
a A
L
g
V
A
L
F
Y
l
l
r
=
= .....(1)
When the load is immersed in the liquid, then
w
w A
L
)
g
1
V
g
V
(
A
L
F
Y
l
l
´
´
-
r
=
¢
= ....(2)
(Q Now net weight = weight – upthrust)
From eqs. (1) and (2), we get
w
a
)
1
(
l
l
-
r
=
r
or
)
( w
a
a
l
l
l
-
=
r
23. (c) Energy stored per unit volume
= strain
stress
2
1
´
´
= )
modulus
s
'
Young
/
stress
(
stress
2
1
´
´
= )
modulus
s
'
Young
/(
)
stress
(
2
1 2
´ =
Y
2
S2
24. (c)
25. (c) For a perfectly rigid body strain produced is zero for
the given force applied, so
Y = stress/strain = ¥
EXERCISE - 2
1. (b) Let W newton be the load suspended. Then
1
1
1
1
A
L
W
)
L
/
(
)
A
/
W
(
Y
l
l
=
= ...(1)
and
2
2
2
2
A
L
W
)
L
/
(
)
A
/
W
(
Y
l
l
=
= ....(2)
Dividing equation (1) byequation (2), we get
÷
ø
ö
ç
è
æ
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
÷
÷
ø
ö
ç
ç
è
æ
=
1
2
A
A
1
1
2
1
2
1
2
l
l
l
l
1
2
2
1 =
l
l
or l1 : l2 = 2 : 1
2. (c) Given that F/A = 4.8 × 107 Nm–2
F = 4.8 ×107 ×Aor
2
7 6
mv
4.8 10 10 48
r
-
= ´ ´ =
or 48
r
r
m 2
2
=
w
or
r
m
48
2
=
w
sec
/
rad
4
16
3
.
0
10
48
=
=
÷
ø
ö
ç
è
æ
´
=
w
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-258-320.jpg)
![255
Mechanical Properties of Solids
3. (b) We know that Y= F L/pr2 l or r2 = F L/(Yp l)
)
Y
/(
L
F
R B
2
B l
p
= and )
Y
/(
L
F
R S
2
S l
p
=
or 2
10
10
2
Y
Y
R
R
10
10
B
S
2
S
2
B
=
´
=
=
or 2
S
2
B R
2
R = or S
B R
2
R =
2
/
R
R B
S =
4. (d) F =YAat = (2.0 × 1011) (10–6) (1.1 × 10–5) (20)
= 44 newton
5. (d)
6. (d) Elastic energy = x
F
2
1
´
´
F=200 N, x=1 mm=10–3 m
J
1
.
0
10
1
200
2
1
E 3
=
´
´
´
= -
7. (a) U/ volume =
2
strain
Y
2
1
´ = 3600 J m–3
[Strain = 0.06 × 10–2]
8. (b)
2
l
F Y A F r
L
= ´ ´ Þ µ (Y, l and and Lare constant)
Ifdiameter is madefour times then force required will
be 16 times, i.e., 16 × 103 N
9. (b)
2
8
.
0
100
1
r
´
=
q
=
f
l
= 0.004 radian
10. (d) Q Both wires are same materials so both will have
sameYoung’s modulus, and let it beY.
( )
ΔL/L
A.
F
strain
stress
Y =
= , force
applied
F =
A area of cross-section of wire
=
Now, 2
1 Y
Y =
( )( ) ( )( )
2
2
1
1 L
A
FL
L
A
FL
D
=
D
Þ
Since load and length are same for both
2
2
2
1
2
1 L
r
L
r D
=
D
Þ , 4
r
r
L
L
2
1
2
2
1
=
÷
÷
ø
ö
ç
ç
è
æ
=
÷
÷
ø
ö
ç
ç
è
æ
D
D
1 2
L : L 4:1
D D =
11. (d) 2 (1 )
Y = h + s
2.4 2 (1 ) 1.2 1 0.2
h = h + s Þ = + s Þ s =
12. (b) Bulk modulus
V
PV
)
V
/
V
(
P
B
D
-
=
D
-
= ....(1)
and T
.
V
.
3
T
V
V a
=
D
g
=
D or
.
T
.
3
1
V
V
a
=
D
-
...(2)
From eqs. (1) and (2), )
T
.
3
/(
P
B a
= or
B
3
P
T
a
=
13. (a)
P
V
/
V
B
1
K
D
=
= . Here, P = 100 atm,
K = 4 ×10–5 andV =100cm3.
Hence, DV=0.4cm3
14. (a)
I
=
d
Y
3
W 3
l
, where W= load, l= length of beam and I is
geometrical moment ofinertia for rectangular beam,
3
bd
Ι
12
= where b = breadth and d = depth
For square beam b = d
4
1
b
Ι
12
=
For a beam of circular cross-section,
4
2
πr
Ι
4
æ ö
=ç ÷
è ø
4
3
4
3
1
b
Y
W
4
b
Y
3
12
W l
l
=
´
=
d (for sq. cross section)
and
)
r
(
Y
3
W
4
)
4
/
r
(
Y
3
W
4
3
4
3
2
p
=
p
=
d
l
l
(forcircular cross-section)
Now
p
=
p
p
=
p
=
d
d 3
)
r
(
r
3
b
r
3
2
2
4
4
4
2
1
( 2 2
b π r
=
Q i.e., theyhave same cross-sectional area)
15. (d)
Weight of load Weight of puller
Compressive stress
area
+
=
5
6
20A d 10 5 10
1.6 10
area
´ ´ + ´
Þ = ´
Where d is the density.
3 5
6
20A 2.5 10 10 5 10
1.6 10
A
´ ´ ´ + ´
= ´
ie, 5× 105 = 1.1× 106A or A= 0.45m2
16. (a)
l
l 2
r
C
,
2
)
r
r
(
C
4
2
4
1
4
2
1
ph
=
-
ph
=
Initial volume= Final volume
r
p
=
r
-
p l
l 2
2
1
2
2 r
]
r
r
[
)
r
r
)(
r
r
(
r
r
r
r 1
2
1
2
2
2
1
2
2
2
-
+
=
Þ
-
=
Þ
)
98
.
7
02
.
8
)(
98
.
7
02
.
8
(
r2
-
+
=
Þ
cm
8
.
0
r
cm
64
.
0
04
.
0
16
r2
=
Þ
=
´
=
Þ
4
4
4
4
4
1
4
2
2
1
]
8
.
0
[
]
98
.
7
[
]
02
.
8
[
r
r
r
C
C -
=
-
=
17. (a) Weights without and with liquid proportional to rb
and rb – rl.
18. (b)
19. (c) d
For a beam, the depression at the centre is given by,
3
f L
4Ybd
æ ö
d = ç ÷
è ø
[f, L, b, d are constants for a particular beam]
i.e.
1
Y
d µ](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-259-320.jpg)

![257
Mechanical Properties of Solids
34. (b) The atoms when brought from infinity are attracted
due to interatomic electrostatic force of attraction. At
point B, the potential energyis minimum and force of
attraction is maximum. But if we bring atoms closer
than x = B, forceof repulsion between two nuclei starts
and P.E. increases.
x
B
C
P.E.
A
35. (c)
F
x
Fcom Fext
From the figure, it is clear that
Fcom < Fext.
36. (d)
4
. Constant
2
r
r C
L
ph q
= q = =
4 4
0 0
( ) ( / 2) ( ')
2 2( / 2)
r r
l l
ph q -q ph q -q
Þ =
l/2
l
q0
q
q¢ = 0
0 0
0
( ) 8
2 16 9
q- q q
Þ = Þ q = q
37. (a)
6
3
10 100
34
3
3 10 10
S
L m
dg
= = = =
´ ´
38. (b)
r 6mm 30
r 0.18
1m
q ´ °
q = f Þ f = = = °
l
l
39. (a) F YA YA
D
= = aDq
l
l
= 2 × 1011 × (1 × 10–6) × 1.1 × 10–5 × (10) = 22 N
40. (a) 2
mg
Y
( / 4) d x
=
p
l
.........(1)
max
dY m d x
2
Y m d x
D D D D
æ ö
= + + +
ç ÷
è ø
l
l
m = 20.0 kg Þ Dm= 0.1 kg
l = 125cm Þ Dl = 1 cm.
d =0.050 cm. Þ Dd = 0.001 cm
x= 0.100 cm. Þ Dx=0.001cm.
max
0.1kg 1cm
dY 20.0kg 125cm 100% 6.3%
0.001cm 0.001cm
Y 2
0.05cm 0.100cm
æ ö
+
ç ÷
æ ö
= ´ =
ç ÷ ç ÷
è ø
+ ´ +
ç ÷
è ø
41. (d) Given, 1
2
,
l
a
l
= 1
2
r
b
r
= , 1
2
Y
c
Y
=
Brass
T
T
2g
Steel
T
2g
Let Young’s modulus of steel beY1, and that of brass
be Y2
1 1
1
1 1
F l
Y
A l
=
D …(i)
and
2 2
2
2 2
F l
Y
A l
=
D …(ii)
Dividing equation (i) byequation (ii), we get
1 1 2 1 2
2 2 1 2 1
Y F A l l
Y F A l l
D
=
D …(iii)
Force on steel wire from free bodydiagram
1 (2 ) Newton
T F g
= =
Force on brass wire from free bodydiagram
2 1 2 4 Newton
F T T g g
= = + =
Now putting the value of F1, F2 in equation (iii), we
get
2
1 2 1 2 2
2 2
2 2 1 1
1
2 1 1
. . .
4 2
Y r l l l
g
a
Y g l l l
r b
æ ö é ù æ ö æ ö
æ ö p D D
æ ö
= =
ç ÷ ê ú ç ÷
ç ÷ ç ÷ ç ÷
è ø
è ø D D
è ø è ø
p
è ø ë û
42. (d) If side of the cube is L then
3
3
dV dL
V L
V L
= Þ =
% change in volume = 3 × (% change in length)
= 3 × 1% = 3%
Bulk strain 0.03
V
V
D
=
43. (b)
2
2
4 9.8
19.6 10
2 10
F
K
x -
´
= = = ´
´
Work done =
2 2
1
19.6 10 (0.05) 2.45
2
J
´ ´ =
44. (d) F =
YA
L
× l
So, extension, lµ
L
A
µ 2
L
D
[Q F and Y are
constant]
l1 µ 2
100
1
µ 100 and l2 µ 2
200
2
µ 50
l3µ 2
300
3
µ
100
3
and l4 µ
50
1
4
µ 200
The ratio of
2
L
D
is maximum for case (d).
Hence, option (d) is correct.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-261-320.jpg)
![258 PHYSICS
45. (a) Percentage elongation in the wire
F
AY
=
l
4
2 11
6.28 10 (1) 1
1000
(0.01) 2 10
´ ´
= =
p ´ ´
46. (a) Work done 2
1 1
Stress Strain (Strain)
2 2
Y
= ´ ´ = ´ ´
Since, elasticity of steel is more than copper, hence
more work has to be done in order to stretch the steel.
47. (b) Stress is defined as internal force (restoring force) per
unit area of a body. Also, rubber is less elastic than
steel, because restoring force is less for rubber than
steel.
48. (d) 49. (d) 50. (a)
EXERCISE - 3
Exemplar Questions
1. (b) As liquid is ideal so no. frictional force exists hence,
tangential forces are zero so there is no stress
developed.
2. (d) As we know that,
Breaking stress =
Breaking force
Area of cross-section
..(i)
When length of the wire changes (or byreducing half)
area of cross-section remains same.
Hence, breaking force will be same because breaking
stress does not depend on length.
3. (d) Aswe knowthat, length of awirewhen thetemperature
increased
0 (1 )
t
L L T
= + aD
where DT is change in the temperature.
L0 is original length,
a is coefficient oflinear expansion and
Lt is length at temperature T.
Now, 0 0
t
L L L L T
D = - = aD
Now, Young's modulus (Y)
Stress
Strain
=
0 0
0
1
FL FL
A L AL T T
= = µ
´D aD D
As,
1
Y
T
µ
D
So, if temperature increass DT increases, hence
Young's modulus of elasticity (Y) decreases.
4. (c) When a spring is stretched by applying a load to its
free end. Clearly the length and shape of the spring
changes. So strain produced when change in length
corresponds to longitudinal strain andchange in shape
corresponds to shearing strain.
5. (b) As we know that,
The Young's modulus
Stress /
Strain /
F A F L
Y
L L A L
= = = ´
D D
2 2
4
( / 2)
F L FL
L
D D L
= ´ =
D
p p D
2 4 4
FL FL
D D
LY LY
= Þ =
pD pD
If F and
L
L
D
are constants.
So,
1
D
Y
µ
Hence, we can find ratio as
copper iron
iron copper
D Y
D Y
=
6. (a) Consider the given diagram
m
90°–q
90°–q
q q
x
O
B
A C
L L
So, change in length
0 0
( ) ( )
L A B AC CB
D = + - +
= 2BO – 2AC
= 2 [BO – AC] ( AO = BO, AC = CB)
2 2 1/ 2
2[( ) ]
x L L
= + -
1/ 2
2
2
2 1 1
x
L
L
é ù
æ ö
ê ú
= + -
ç ÷
ç ÷
ê ú
è ø
ë û
2 2
2
1
2 1 1
2
x x
L L
L
L
é ù
D » + - =
ê ú
ë û
[ ]
x L
<<
Q
2 2
2
/
Strain =
2 2 2
L x L x
L L L
D
= =
7. (c) Let us consider the free body diagram of the
rectangular frame
Tsinq Tsinq
T
Tcosq
Tcosq
q
q
m
mg
Net forces acting on frame will be zero.
So, Balancing vertical forces
2T sinq – mg = 0 [T is tension in the string]
2T sinq = mg ...(i)
Total horizontal force
cos cos 0
T T
= q - q =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-262-320.jpg)
![259
Mechanical Properties of Solids
Nowfrom Eq. (i),
2sin
mg
T =
q
max
min
2sin
mg
T =
q
As mg is constant then
1
sin
T µ
q
min min
sin 0 0
q = Þ q =
No option matches with q = 0°
min
max
2sin
mg
T =
q
(since, sinqmax = 1)
max
sin 1 90
q = Þ q = °
So tension is all three cases are different rejects option
(a)
For minimum tension q must be 90° i.e. sin q = 1
Hence, tension is the least for the case (b).
8. (d) A mass M is attached at the centre or midpoint of rod
of rubber and steel. As the mass is attached to both
the rods, both rod will be elongated as shown in
figuresbut due todifferent elasticproperties ofmaterial
rubber changes shape also.
M M
(Steel)
(Rubber)
As the Young's modulus of rigidity for steel, is larger
than rubber, so strain
L
L
D
for rubber is larger than
steel for same stress.
NEET/AIPMT (2013-2017) Questions
9. (d) F =
YA
L
× l! So, extension, lµ
L
A
µ 2
L
D
[Q F and Y are constant]
l1 µ 2
100
1
µ 100 and l2 µ 2
200
2
µ 50
l3µ 2
300
3
µ
100
3
and l4 µ
50
1
4
µ 200
The ratio of
2
L
D
is maximum for case (d).
Hence, option (d) is correct.
10. (c) From formula,
Increase in length 2
4
FL FL
L
AY D Y
D = =
p
2
S S C C S
C C S S C
L F D Y L
L F D Y L
æ ö
D
= ç ÷
D è ø
=
2
7 1 1
5
q
p s
æ ö æ ö
´ç ÷ ç ÷
è ø
è ø
= 2
7
(5 )
q
sp
11. (b) As Y=
F
F
A
AY
Þ D =
D
l
l
l
l
But V = Al soA=
V
l
Therefore Dl =
2
2
F
VY
µ
l
l
Hence graph of Dl versus l2 will give a straight line.
12. (b) Compressibilityof water,
K = 45.4 × 10–11 Pa–1
densityof water P = 103 kg/m3
depth of ocean, h = 2700 m
We have to find
V
?
V
D
=
As we know, compressibility,
K=
1 ( V / V)
(P gh)
B P
D
= = r
So, (DV/V)= Krgh
= 45.4 × 10–11 × 103 ×10 ×2700 = 1.2258× 10–2
13. (a) Young's modulusY =
W
.
A
l
l
D
1 2
1 2
W W
Y Y
= [Q A, l, Dl same for both brass and steel]
Brass
A, ,
l Dl
Steel
l, A, Dl
Y2 Y1
1 1
2 2
W Y
2
W Y
= = [Ysteel/Ybrass = 2 given]
14. (c) Bulk modulus is given by
B =
P
V
V
D
æ ö
ç ÷
è ø
or
V P
V B
D
=
R P
3
R B
D
= (here,
R
R
D
= fractional decreases in radius)
R P
R 3B
D
Þ =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-263-320.jpg)
![260 PHYSICS
FLUIDS
Fluid is something that can flow. All liquids and gases are fluids.
The force exerted normally at a unit area of the surface of a fluid
is called fluid pressure.
i.e., P =
F
a
Its S.I. unit is Nm–2 or Pascal. Its dimensions are [ML–1T–2].
PASCAL'S LAW AND ITS APPLICATIONS
Pascal's law : Pressure in a fluid in equilibrium is the same
everywhere, if the effect of gravity is neglected.
Another form of Pascal's law : The excess pressure, applied
anywhere in a mass of confined incompressible fluid is
transmitted by the fluid in all directions without being
diminished in magnitude.
Applications of Pascal's Law
Hydraulic lift : Its working is based on Pascal's law. Apiston of
small cross-sectional area (a) exerts a force (f) on the liquid.
Applied force = f
F = pA
f = pa
Area = a
Area = A
The pressure is transmitted undiminished to the larger cylinder
of cross-sectional area A.
= =
f F
P
a A
Þ =
A
F f
a
Hydraulic brakes also work on pascal's law.
ATMOSPHERIC, HYDROSTATIC AND GUAGE PRESSURE
Atmospheric pressure : The atmosphere exerts pressure on the
earth's surface. The atmospheric pressure at sea level is given by
P0 = 1.01 × 105 Pa
Hydrostatic pressure : The hydrostatic pressure at a depth h
below the surface of a fluid is given by
P = hrg
where r is the density of the fluid, g acceleration due to gravity
and h is the depth of the liquid column.
Gauge pressure : The pressure at anypoint in a fluid is equal to
the sum of the atmospheric pressure acting on its surface and the
hydrostatic pressure due to the weight of the fluid above that
point which is at a depth h below the surface of the fluid.
The gauge pressure is given by
P = P0 + hrg
or, P – P0 = hrg
BUOYANCY AND ARCHIMEDES' PRINCIPLE
Buoyancy
If a body is partiallyor wholly immersed in a fluid, it experiences
an upward force due tothe fluid surrounding it. The phenomenon
of force exerted by fluid on the body called buoyancy and the
force is called buoyant force or upthrust.
A bodyexperiences buoyant force whether it floats or sinks, under
its own weight or due to other forces applied on it.
Archimedes' Principle
When any body is immersed (totally or partially) in a liquid it
appears to lose part of its weight and the apparent loss of weight
is equal to the weight of liquid displaced.
Let a bodyof weight W is immersed in a fluid and W' is upthrust
on it then
(i) if W > W', then body will sink.
(ii) if W = W', then the bodyfloats with whole or some part of
its volume inside the fluid.
Let V be the volume of a body of density d and V' be the
volume of liquid of density r displaced. If the body floats
then Vd = V¢r
V
'
V
d
=
r
gives the fraction of the volume inside the liquid
in which the body floats.
Also, body immersed in a fluid experiences an upward buoyant
force equivalent to the weight of the fluid displaced by it.
The proof of this principle is very simple. Imagine a body of
arbitrary shape completely immersed in a liquid of density r as
10
Mechanical
Properties of Fluids](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-264-320.jpg)
![261
Mechanical Properties of Fluids
shown in the figure (a). Abody is being acted upon by the forces
from all directions. Let us consider a vertical element of height h
and cross-sectional area dA (as shown in the figure (b)).
h2
dA
h
h1 F1
F2
(a) (b)
The force acting on the upper surface of the element is F1
(downward) and that on the lower surface is F2 (upward). Since
F2 > F1, therefore, the net upward force acting on the element is
dF = F2 – F1
It can be easily seen from the figure (b), that
1 1
F ( gh )dA
= r and 2 2
F ( gh )dA
= r so dF g(h)dA
= r
Also, h2 – h1 = h and d (dA) = dV
The net upward force is F gdV Vg
= r = r
ò
Hence, for the entire body, the buoyant force is the weight of the
volume of the fluid displaced.
The buoyant force acts through the centre of gravity of the
displaced fluid.
Keep in Memory
1. The pressure is perpendicular to the surface of the fluid.
2. The upthrust on a body immersed in a liquid does not
depend on the mass, density or shape of the body. It only
depends on the volume of the body.
3. The weight of the plastic bag full of air is same as that of
the empty bag because the upthrust is equal to the weight
of the air enclosed.
4. The cross-section of the water stream from a top decreases
as it goes down in accordance with the equation of
continuity.
5. We cannot sip a drink with a straw on the moon, because
there is no atmosphere on the moon.
6. The line joining the centre of gravity and centre of
buoyancy is called central line.
7. Metacenter - is a point where the vertical line passing
through the centre of buoyancy intersects the central line.
8. The floating body is in stable equilibrium when the
metacenter is above the centre of gravity(centre of gravity
is below the centre of buoyancy).
9. The floating bodyis in the unstable equilibrium when the
metacenter lies below thecentre ofgravity(centre of gravity
is above the centre of buoyancy).
10. The floating bodyis in the neutral equilibriumwhen centre
of gravity coincides with the metacenter (centre of gravity
coincides with the centre of buoyancy).
11. The wooden rod cannot float vertically in a pond of water
because centre of gravity lies above the metacenter.
12. (i) If a body just floats in a liquid (density of the body is
equal to the densityof liquid) then the bodysinks if it
is pushed downwards.
(ii) If two bodies have equal upthrust when just immersed
in a liquid, both will have the same volume.
(iii) If a person floats on his back on the surface of water,
the apparent weight of person is zero.
13. The hydrometer can be used to measure density of the
liquid or fluid.
Relative Density (or Specific Gravity)
Liquids may be treated as incompressible. Hence their density
may be assumed to be constant throughout.
Relative density =
Weight of substance in air
Weight of equal volume of water
=
Weight of substance in air
Loss of weight in water
4º
=
Density of substance
Density of water at C
Density in SI system = 1000 × density in the cgs system.
(i) The density of liquid of bulk modulus B at a depth h is
given by 0 1
h
gh
B
r
æ ö
r = r +
ç ÷
è ø
where 0
r is the density of
liquid on its surface and r is the average densityof liquid.
(ii) The density of liquid changes with pressure as
0 1
h
P
P P
B
D
æ ö
= +
ç ÷
è ø
where =
DP change in pressure and B = bulk modulus of
liquid.
(iii) If two liquids of masses m1, m2 and densities r1, r2 are
mixed together, then the density of the mixture is given by
1 2
1 2
1 2
m m
m m
+
r =
+
r r
And if m1 = m2 but different densities are mixed together,
then the density of the mixture is harmonic mean of the
densities.
i.e.,
2
1
2
1
2
r
+
r
r
r
=
r or ú
û
ù
ê
ë
é
r
+
r
=
r
1
2
1
1
1
2
1
(iv) If two drops of same volume but different densities are
mixed together, then the density of the mixture is the
arithmetic mean of the densities.
i.e.,
2
2
1 r
+
r
=
r (as
1 0 2 0
0 0
V V
V V
r + r
r =
+
)
SURFACE TENSION
It is defined as the force per unit length acting at right angles
on either side of an imaginary line drawn on the free surface of
the liquid.
i.e., =
l
F
S
The surface tension is also defined as the work required to
increase unit area of that liquid film.
Its SI unit is N/m or J/m2 and dimensions are [ML0T–2].](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-265-320.jpg)


![264 PHYSICS
From eqns. (1) and (2), V = V1
Hence, no change in the level of water.
Example3.
Two substances of densities r1 and r2 are mixed in equal
volume and the relative density of mixture is 4. When they
are mixed in equal masses, the relative density of the
mixture is 3. Determine the values of r1 and r2 .
Solution :
When the substances are mixed in equal volumes, then
4
V
2
V
V 2
1 ´
=
r
+
r ... (1)
When the two substances are mixed in equal masses, then
3
m
2
m
m
2
1
=
r
+
r
...(2)
From eq. (1), 8
2
1 =
r
+
r ... (3)
From eqn. (2)
3
2
or
3
2
1
1
2
1
2
1
2
1
=
r
r
r
+
r
=
r
+
r
or 12
or
3
2
8
2
1
2
1
=
r
r
=
r
r
. ...(4)
Now
2
/
1
2
1
2
2
1
2
1 ]
4
)
[( r
r
-
r
+
r
=
r
-
r
4
]
48
64
[ 2
/
1
=
-
= ...(5)
Solving eqns. (3) and (5), we get 6
1 =
r and 2
ρ 2
= ]
Example4.
A sealed tank containing a liquid of density r moves with
a horizontal acceleration a, as shown in fig. Find the
difference in pressure between the points A and B.
C A
B
h
a
l
Solution :
Since points A and C are in the same horizontal line but
separated by distance l and liquid tank is moving
horizontallywith acceleration a, hence
PC – PA = lra or PC = PA + lra
Points B and C are vertically separated by h
PB – PC = h r g
or PB – (PA + l r a) = h r g
or PB – PA = h r g + l ra
Example5.
Calculate the excess pressure within a bubble of air of
radius 0.1 mm in water. If the bubble had been formed 10 cm
below the water surface when the atmospheric pressure
was 1.013 × 105 Pa, then what would have been the total
pressure inside the bubble?
Solution :
Excess pressure within air bubble
=
2T
r
=
3
3
2 73 10
0.1 10
-
-
´ ´
´
= 1460 Pa
The pressure at a depth d, in liquid P = hdg. Therefore, the
total pressure inside the air bubble is
Pin = Patm + hdg +
2T
r
or Pin = 1.013× 105 + 10 ×10–2 × 103 × 9.8 + 1460
= 101300 + 980 + 1460
=103740 =1.037 ×105 Pa.
Example6.
A capillary of the shape as shown is dipped in a liquid.
Contact angle between the liquid and the capillary is 0°
and effect of liquid inside the meniscus is to be neglected. T
is the surface tension of the liquid, r isradius of the meniscus,
g is acceleration due to gravity and r is density of the
liquid then determine the height h in equilibrium.
h
Solution :
As weight ofliquidin capillaryisbalancedbysurfacetension,
then 2
1
T 2 r r h g
´ p = p r (for a tube ofuniform radius r)
1
2T
h
r g
=
r
r
h1
But weight ofliquid in tapered tube ismore than uniform tube
of radius r, then in order to balance h < h1.
2T
h
r g
<
r
r
Example7.
A hydraulic automobile lift is designed to lift car with a
maximum mass of 3000 kg. The area of cross-section of the
piston carrying the load is 425 cm2. What maximumpressure
would the smaller piston have to bear ?
Solution :
Here mass ofcar = 3000 kg.
Area of cross section of larger piston
= 425cm2 = 425 ×10–4 m2.
The maximum pressure that the smaller piston would
have to bear
= 4
Weight of car 3000 9.8
Area of cross-section 425 10-
´
=
´
5 2
6.92 10 Nm-
= ´](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-268-320.jpg)


![267
Mechanical Properties of Fluids
VELOCITY OF EFFLUX AND TORRICELLI'S THEOREM
(i) Torricelli's theorem : For liquid filled in a tank upto a
height H having a hole O at a depth h from free level of
liquid through which the liquid is coming out, velocity of
efflux of liquid v = 2gh .
(ii) Time taken by the liquid in falling from hole to ground
level
2( )
-
=
H h
t
g
H
h
Free
surface
(iii) The horizontal range covered by the liquid
x = horizontal velocity (v) ×time (t)
2( )
2
-
= ´
H h
gh
g
2 ( )
= -
h H h .
For maximum horizontalrange, differentiating both sidew.r.t.
h and we get h = H/2, the range is maximum.
Keep in Memory
1. The cross-section of the water stream from a top decreases
as it goes down in accordance with the equation of
continuity.
2. When a hale blows over a roof, the force on the roof is
upwards.
3. Sudden fall in atmospheric pressure predicts possibility of
a storm.
4. Venturimeter is a device used for the measurement of the
rate of flow of incompressible fluid through a tube. Its
working is based on Bernoulli’s principle.
Example8.
The vessel of area of cross-section A has liquid to a height
H. There is a hole at the bottom of vessel having area of
cross-section a. Find the time taken to decrease the level
from H1 to H2.
Solution :
The average velocity of efflux, 1 2
2g H 2g H
v
2
+
=
Let t be the time taken to empty the tank from level H1 to
H2.
Then, ]
H
H
[
A
t
a
2
H
g
2
H
g
2
2
1
2
1
-
=
´
´
+
or t
( ) ( )
( )( )ú
ú
û
ù
ê
ê
ë
é
-
+
-
´
-
´
÷
÷
ø
ö
ç
ç
è
æ
´
=
2
1
2
1
2
1
2
1
H
H
H
H
H
H
H
H
g
2
a
A
( )
2
1 H
H
g
2
a
A
-
´
÷
÷
ø
ö
ç
ç
è
æ
´
=
( )
1 2
A 2
H H
a g
æ ö
= ´ ´ -
ç ÷
è ø
Example9.
In a test experiment on a model aeroplane in a wind tunnel,
the flow speeds on the upper and lower surfaces of the
wing are 70 m/s and 63 m/s respectively. What is the lift on
the wing if its area is 2.5 m2 ? Take the density of air to be
1.3 kg m–3.
Solution :
Let v1 be the speed and P1 be the pressure on the upper
surface of the wing, and corresponding values on the lower
surface be v2 and P2 respectively.
v1 = 70 m/s, v2 = 63 m/s, A= 2.5 m2,
P =1.3 kg m–3.
According to Bernoulli’s theorem
2 2
1 1 2 2
1 1
P v P v
2 2
+ r = + r
2 2
2 1 1 2
1
P P (v v )
2
- = r - =
2 2
2 1
1
P P 3 (70 63 )
2
- = ´ ´ -
Force (lift) on the wing = 2 1
A (P P )
-
=
2 2
1
2.5 1.3 (70 63 )
2
´ ´ ´ -
=
1
2.5 1.3 133 7
2
´ ´ ´ ´
3
1.5 10 N
= ´
Example10.
In Millikan’s oil drop experiment, what is the terminal
speed of an uncharged drop of radius 2.0 × 10–5 m and
density 1.2 × 103 kg m–3. Take the viscosity of air at the
temperature of the experiment to be 1.8 × 10–5 Pa s. How
much is the viscous force on the drop at that speed ? Neglect
buoyancy of the drop due to air.
Solution :
Here, r = 2.0 × 10–5 m, r = 1.2 × 103 kg m–3,
h = 1.8 × 10–5 Pa s.
From formula, terminal velocity
2
2 r ( ) g
V
9
r - s
=
h
Þ
5 2 3
5
2 (2 10 ) (1.2 10 0) 9.8
V
9 1.8 10
-
-
´ ´ ´ - ´
=
´ ´
2 1
5.8 10 ms
- -
= ´
Now viscous force on the drop
F= 6phrv
Þ 5 5 2
22
F 6 (1.8 10 ) (2 10 ) 5.8 10
7
- - -
= ´ ´ ´ ´ ´ ´ ´
= 3.93 × 10–19 N](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-271-320.jpg)






![274 PHYSICS
Exemplar Questions
1. A tall cylinder is filled with viscous oil. A round pebble is
dropped from the top with zero initial velocity. From the plot
shown in figure, indicatethe one that represents the velocity
(v) of the pebble as a function of time (t) .
v
t
(a)
v
t
(b)
v
t
(c)
v
t
(d)
2. Which of the following diagrams does not represent a
streamline flow?
(b)
(a)
(d)
(c)
3. Along a streamline,
(a) the velocityof a fluid particle remains constant
(b) the velocity of all fluid particles crossing a given
position is constant
(c) the velocity of all fluid particles at a given instant is
constant
(d) the speed of a fluid particle remains constant
4. An ideal fluid flows through a pipe of circular cross-section
made of two sections with diameters 2.5 cm and 3.75 cm.
The ratio of the velocities in the two pipes is
(a) 9: 4 (b) 3: 2 (c) 3 : 2 (d) 2 : 3
5. The angle of contact at the interface of water-glass is 0°,
ethyl alcohol-glass is 0°, mercury-glass is 140° and
methyliodide-glass is 30°.Aglass capillaryis put in a trough
containing one of these four liquids. It is observed that the
meniscus is convex. The liquid in the trough is
(a) water (b) ethylalcohol
(c) mercury (d) methyliodide
NEET/AIPMT (2013-2017) Questions
6. The wetability ofa surface by a liquid depends primarilyon
(a) surface tension [2013]
(b) density
(c) angle of contact between the surface and the liquid
(d) viscosity
7. A fluid is in streamline flow across a horizontal pipe of
variable area ofcross section. For this which of the following
statements is correct? [NEET Kar. 2013]
(a) The velocity is minimum at the narrowest part of the
pipe and the pressure is minimum at the widest part of
the pipe
(b) The velocity is maximum at the narrowest part of the
pipe and pressure is maximum at the widest part of the
pipe
(c) Velocity and pressure both are maximum at the
narrowest part of the pipe
(d) Velocityand pressure both are maximum at the widest
part of the pipe
49. Statement 1 : Falling raindrops acquire a terminal velocity.
Statement 2 : A constant force in the direction of motion
and a velocity dependent force opposite to the direction of
motion, always result in the acquisition of terminal velocity.
50. Statement 1 : Thebuoyant force on a submerged rigid object
can be considered to be acting at the centre of mass of the
object.
Statement 2 : For a rigid body a force field distributed
uniformlythrough its volume can be considered tobe acting
at the centre of mass of the body.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-278-320.jpg)
![275
Mechanical Properties of Fluids
8. A certain number ofspherical drops of a liquid of radius ‘r’
coalesce to form a single drop ofradius ‘R’ and volume ‘V’.
If ‘T’ is the surface tension of the liquid, then : [2014]
(a) energy =
1 1
4VT
r R
æ ö
-
ç ÷
è ø
is released
(b) energy =
1 1
3VT
r R
æ ö
+
ç ÷
è ø
is absorbed
(c) energy =
1 1
3VT
r R
æ ö
-
ç ÷
è ø
is released
(d) energy is neither released nor absorbed
9. A wind with speed 40 m/s blows parallel to the roof of a
house. The area of the roof is 250 m2. Assuming that the
pressure inside the house is atmospheric pressure, the force
exerted by the wind on the roof and the direction of the
forcewill be (rair = 1.2 kg/m3) [2015]
(a) 4.8 × 105 N, upwards
(b) 2.4 × 105 N, upwards
(c) 2.4 × 105 N, downwards
(d) 4.8 × 105 N, downwards
10. The cylindrical tube ofa spray pump has radius, R, one end
ofwhich has n fine holes, each ofradius r. Ifthe speed of the
liquid in the tube is V, the speed of the ejection of the liquid
through the holes is : [2015 RS]
(a)
2
2
VR
nr
(b)
2
3 2
VR
n r
(c)
2
V R
nr
(d)
2
2 2
VR
n r
11. Water rises to a height 'h' in a capillarytube. If the length of
capaillarytube above the surface of water is made less than
'h' then : [2015 RS]
(a) water rises upto the top of capillary tube and stays
there without overflowing
(b) water rises upto a point a little below the top and stays
there
(c) water does not rise at all.
(d) Water rises uptothe tip of capillarytube and then starts
overflowing like fountain.
12. Two non-mixing liquids of densities r and nr(n > 1) are put
in a container. Theheight ofeach liquid is h.Asolid cylinder
oflength Land densityd is put in thiscontainer. Thecylinder
floats with its axis vertical and length pL(p < 1) in the denser
liquid. The density d is equal to : [2016]
(a) {1 + (n + 1)p}r (b) {2 + (n + 1)p}r
(c) {2 + (n – 1)p}r (d) {1 + (n – 1)p}r
13. A U tube with both ends open tothe atmosphere, is partially
filledwith water.Oil,whichisimmisciblewithwater,ispoured
intoone side until it stands at a distance of10 mm above the
water level on the other side. Meanwhile the water rises by
65 mm from its original level (see diagram). The densityof
the oil is [2017]
A
Oil
B C
Water
Initial water level
Final water level
10 mm
Pa
Pa
F
E
D
65 mm
65 mm
(a) 425 kg m–3 (b) 800 kg m–3
(c) 928 kg m–3 (d) 650 kg m–3](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-279-320.jpg)



![279
Mechanical Properties of Fluids
3. (b) In streamline flow, the speed of liquid of each particle
at a point in a particular cross-section is constant,
between two cross-section of a tube of flow because
AV = constant (law of continuity).
4. (a) As given that,
Diameter at 1st section (d1) = 2.5.
Diameter at 2nd section (d2) = 3.75.
According to equation of continuity,
for cross-sections A1 and A2.
A1v1 = A2v2
2
2
1 2 2 2
2
2 1 1
1
( )
( )
v A r r
v A r
r
æ ö
p
= = = ç ÷
p è ø
2
2
2
2
2
1
1
2
2
d
d
d
d
æ ö
ç ÷ æ ö
è ø
= = ç ÷
è ø
æ ö
ç ÷
è ø
2 1
2 1
,
2 2
d d
r r
é ù
= =
ê ú
ë û
Q
2
3.75 9
2.5 4
æ ö
= =
ç ÷
è ø
1 2
: 9 : 4
v v
=
5. (c) We observed that meniscus of liquid is convex shape
as shown in figure which is possible if only, the angle
of contact is obtuse. Hence, the combination will be of
case of mercury-glass (140°). Hence verifies the option
(c).
140°
convex
mercury
NEET/AIPMT (2013-2017) Questions
6. (c) Wetability of a surface by a liquid primarily depends
on angle of contact between the surface and liquid.
If angle of contact is acute liquids wet the solid and
vice-versa.
7. (b) According to Bernoulli’s theorem,
2
1
2
P v
+ r = constant and Av
v = constant
IfA isminimum,v ismaximum,Pisminimum.
8. (c) As surface area decreases so energy is released.
Energy released = 4pR2T[n1/3 – 1]
where R = n1/3r
=
3 1 1
4 R T
r R
é ù
p -
ê ú
ë û
=
1 1
3VT
r R
é ù
-
ê ú
ë û
9. (b) According to Bernoulli’s theorem,
1 2
2 0
P v P 0
+ r = +
So,DP =
1
2
rv2
F = DPA =
1
2
rv2A P0
P
=
1
2
×1.2×40 ×40×250
= 2.4 × 105 N (upwards)
10. (a) Inflow rate of volume of the liquid = Outflow rate of
volume of the liquid
pR2V = npr2(v) Þ v=
2 2
2 2
R V VR
n r nr
p
=
p
11. (a) Water rises upto the top of capillary tube and stays
there without overflowing.
12. (d) As we know,
Pressure P = Vdg
r
d
(1 – p)L
nr pL
Here, LA d g = (pL)A(nr)g + (1 – p)LAr g
Þ d = (1 – p)r + pn r = [1 + (n – 1)p]r
13. (c) Here, oil oil water water
h g h g
´r ´ = ´r ´
r0g × 140 × 10–3 = rwg × 130 × 10–3
roil =
3 3
130
10 928kg / m
140
´ » [Q rw= 1 kgm–3]](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-283-320.jpg)


![282 PHYSICS
Isothermal and adiabatic elasticities:
(i) Isothermal elasticity, .
P
V
dV
dP
Eiso =
÷
ø
ö
ç
è
æ
-
º
(since PV = RT = constant,
V
P
dV
dP
-
= )
(ii) Adiabatic elasticity,
P
V
dV
dP
Eadia g
=
÷
ø
ö
ç
è
æ
-
= ; where
v
p
C
C
=
g
(iii) iso
adia E
E g
=
Expansionof Gases
There are two coefficients of expansion of gases.
(a) Pressure coefficient of expansion of gas (gP)
0
0
-
g = t
P
P P
P t
where P0 = Pressure at 0°C, Pt = Pressure at t°C
(b) Volume coefficient of expansion of gas (gv)
0
0
-
g = t
v
V V
V t
where V0 = Volume at 0°C, Vt =Volume at t°C
HEAT
Heat is the form of energy which is transferred from one body to
another body due to temperature difference between two bodies.
Thermal energyof a bodyis the sum of kinetic energy of random
motion of the molecules/atoms and the potential energy due to
the interatomic forces.
Calorimeter is an instrument used to measure the heat.
The SIunitofheat isjouleand itsdimensionsare[ML2 T–2]. Other
units of heat are :
(i) Calorie: It is the amount of heat required to raise the
temperatureof1gofwater from14.5ºCto15.5ºC.
1 calorie= 4.2joule. Calorieis theunit ofheat in CGSsystem.
(ii) Kilocalorie,1Kcal= 1000cal
(iii) British Thermal Unit (BTU): It is the fps unit of heat
= 252 cal = amount of heat required to raise the temperature
of1 lb ofwater through 1ºF (from 63°F to 64ºF).
SPECIFIC HEAT CAPACITY
It is the amount of heat required to raise the temperature of unit
mass of substance through 1 degree.
Specific heat capacity, =
´ D
Q
c
m t
Its SI unit is J kg–1K–1
CGS unit cal g–1°C–1
It dimensions are [M0L2T–2q–1]
For gases : During the isothermal process
Dt = 0 Þ c = ¥ (infinite)
Thermal Stress
If a rod fixed at two ends is heated or cooled, then stress are
produced in the rod.
Thermal stress = T
Y D
a
´
0
T strain
æ ö
D
= aD =
ç ÷
è ø
l
l
Effectof Temperature on PendulumClock
A Pendulum clock consists of a metal bar attached with a bob at
oneend and fixed at the other end. Let pendulum clock read correct
time when its length is l0. The time period
t0 = l0
g
2π
Suppose that the temperatureis raised byDT, then newtime period
is
g
t 2
= p
l
=
Þ
l
l
0 0
t
t .....(i)
We have = + aD
l l0(1 t)
Þ = + aD
l
l0
(1 t) .....(ii)
From equations (i) and (ii),
= + aD
0
1
2
t
(1 t)
t
= + aD
1
2
1 t (since a is verysmall)
Þ - = aD
0
t 1
1
t 2
t
-
Þ = aD
0
0
t t 1
t 2
t
so, fractional change in time
D
= aD
0
t 1
t 2
T
Loss of time per day = aD ´
1
2
T 86400 second .
(Q no. of seconds in one day = 86400 sec.)
When temperature increases (during summer), the length of the
pendulum increases due to which the time period increases and
the clock loses time. On the other hand, when temperature
decreases (during winter season), the length decreases and the
time period decrease, the clock in this case, gains time.
Error in scale reading :
As the temperature changes, the length ofthe metal scale changes
so is the difference in graduation
a m
R R (1 T)
= + aD
where Ra = actual reading, Rm = measured reading](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-286-320.jpg)
![283
Thermal Properties of Matter
and during the adiabatic process
Q = 0 Þ c = 0 (zero)
Specific heat of gas : The specificheat ofa gas varies from zeroto
infinity. It may have any positive or negative value.
Following of two specific heats of gas are more significant.
(a) Molar specific heat at constant volume (CV) : It is the
amount of heat required to raise the temperature of
1 mole of a gas through 1K or 1°C at constant volume.
1 Q
T
æ ö
= ç ÷
è ø
V
d
C
n d
(b) Molar specific heat at constant pressure (CP) : It is the
amount of heat required toraise the temperature of1 mole of
a gas through 1K or 1°C at constant pressure.
1
C
æ ö
= ç ÷
è ø
P
dQ
n dT
Mayer’s relation : CP – CV = R
[where R is a gas constant. (R = 8.314 Jmol–1K–1)]
Why CP is greater thanCV ?
When heat is supplied to a gas at constant volume entirely used
to raise its temperature. When a gas is heated at constant pressure,
some work is done in expansion of gas which is in addition to
raise its temperature and hence CP > CV.
THERMAL CAPACITY OR HEAT CAPACITY
It is the amount of heat required to raise the temperature of
substance through 1ºC or 1K.
Thermal capacity = mass × specific heat.
Thisis the relationbetween sp. heat capacity and heat capacity.
Its SI unit is JK–1 CGS unit cal/°C. Its dimensions are [ML2T–
2q–1]
Water Equivalent
It is the mass of water in gram which would require the same
amount of heat to raise its temperature through 1ºC as the body
when heated through the same temperature. It is measured in
gram. Hence
Water equivalent of a body = mass of the body × specific heat
Principle of Heat (or Calorimetry)
When two bodies at different temperatures are placed in contact
with each other then heat will flow from the body at higher
temperature to the bodyat lower temperature until both reach toa
common temperature.
i.e. Heat lost by hot body = heat gained by cold body.
It follows the law of conservation of energy.
LATENT HEAT
It is defined as the amount of heat absorbed or given out by a
body during the change of state while its temperature remaining
constant.
It is of two types :
(i) Latent heat of fusion : It is the quantityof heat required to
change unit mass ofthe solid intoliquid at its melting point.
Latent heat of fusion of ice is 80 cal/g.
(ii) Latentheat ofvaporisation:Itisthequantityofheatrequired
to convert unit mass of liquid into vapour at its boiling
point.
Latent heat of vaporisation of water is 536 cal/g.
Latent heat increases the intermolecular potential energy of the
molecules while kinetic energyremains constant.
Different Processes of Phase Change or State Change
(i) Sublimation : It is the process of conversion of solids to
gaseous state on heating. On cooling the vapours get
converted back into solids.
(ii) Condensation : It is the process of conversion of gases/
vapours toliquid state on cooling. On heating, these liquids
are converted into vapours/gases.
(iii) Boiling : It is the process of conversion of liquid to gaseous
state on heating. It is a cooling process.
(iv) Melting : It is the process in which solid gets converted
intoliquid on heating.
(v) Evaporation : Conversion of liquid intogaseous state at all
temperatures is called evaporation. It is a phenomenon that
occurs at the surface of the liquid.
Melting and boiling occur at definite temperature called melting
point and boiling point respectively. The liquid boils at a
temperature, at which its vapour pressure is equal to the
atmospheric pressure.
Howevaporationisdifferentfromboiling?
Evaporation is a slow process occurring at all the temperature at
the surface ofliquid while boiling is a fast process involving whole
ofthe liquid heated toa particular temperature called boiling point
ofthe liquid.
Keep in Memory
1. The heat capacity or thermal capacitydepends on nature of
the substance (specific heat capacity) and mass of quantity
of matter of the body.
2. In case of melting and boiling, the temperature does not
change, only intermolecular potential energyof the system
changes.
3. System are in thermal equilibrium when their temperature
are same or average kinetic energyper molecule is same.
4. Internal energyis the sum of all energies in a system which
includes energy of translational, rotational as well as
vibrational motion of the molecules.
5. The molar specific heat capacity depends on the molecular
weight of the substance.
6. Thetemperature, volume or pressure ofa system mayremain
constant when it absorbs heat.
7. When we press two block of ice together such that after
releasing the pressure two block join this phenomenon is
called regelation.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-287-320.jpg)

![285
Thermal Properties of Matter
Example5.
From what height must a block of ice be dropped into a
well of water so that 5% of it may melt? Given : both ice
and water are at 0°C, L = 80 cal g–1, J = 4.2 J cal–1 and
g = 980 cm s–2.
Solution :
Let m be the mass of ice. Let h be the height from which
block of ice is dropped. Work done,
W = mgh = m× 980 × h erg
Mass of ice to be melted =
5
m
100
´
Heat required,
5
Q
100
= × m × 80 cal or Q = 4 m cal
[Q L = 80 cal g–1] [Q W= JQ]
Now, m × 980 ×h = J× 4m
7
4.2 10 4m
h
m 980
´ ´
=
´
cm= 1714.3m
[Q J = 4.2 × 107 erg cal–1]
SATURATED AND UNSATURATED AIR
The air is said tobe saturatedwhen the maximum possibleamount
of water vapours are present in it. The pressure of the water
vapours in the saturated air is called saturation vapour pressure.
Ifthe air contains vapours less than the maximum possible amount
possible in the air, then it (air) is said to be unsaturated.
Vapour Pressure
A vapour differs from a gas in that the former can be liqufied by
pressure alone, wheras the latter cannot be liqufied unless it is
first cooled.
If a liquid is kept in a closed vessel, the space above the liquid
becomes saturated with vapour. The pressure exerted by this
vapour is called saturated vapour pressure. Its value depends
only on temperature. It is independent of any external pressure.
Humidity
The humidity shows the presence of water vapours in the
atmosphere. The amount ofwater vapours present per unit volume
oftheair is called absolute humidity.
Relative humidity (RH) is defined as the ratio of the mass of
water vapour (m) actually present in the given volume of air to
the mass of water vapour (M) required to saturate the same
volume at the same temperature. Normally RH is expressed in
percentage
i.e., % 100%
= ´
RH
M
m
RH is also defined as the ratio of actual pressure (p) of water
vapour to the saturated vapour pressure (P) of the water at the
same temperature
i.e., % ×100%
=
p
RH
P
Also,
RH =
Saturated vapour pressure of water at dew point
Saturated vapour pressure of water at room temperature
DewPoint :
It is the temperature at which the amount of water vapours
actuallypresent in a certain volume of the air which is sufficient
to saturate that volume of air.
At the dew point the actual vapour pressure becomes the
saturated vapour pressure.
It means that vapour pressure at room temperature = saturated
vapour pressure(S.V.P) at dew point
If room teperature = dewpoint
then Relative humidity(R.H.) = 100%
Keep in Memory
1. Hygrometry is the branch of thermal physics that deals
with the measurement ofamount of water vapours present
in the atmosphere.
2. Hygrometer is an instrument used todetermine dew point
and relative humidity.
3. Relative humidityis low when the air is dry.
4. Saturated vapours do not obey (except Dalton’s law) gas
laws, while unsaturated vapours obey them. The S.V.P.
varies linearlywith temperature (keeping volume constant)
and equal to one atmospheric pressure at boiling
point.(shown in fig.(a)) S.V.P. constant at constant
temperature on increasing or decreasing volume fig. (b).
V = constant
T
Boiling point
1 atm
(S.V.P.)
(a)
P
T = constant
V
(S.V.P.)
(b)
P
5. At 0ºC, the saturation vapour pessure is 4.6 mm of Hg.
Therefore, water vapours are always present around the
ice. It increases with the increase in temperature.
6. The relative humidity is 100% when thetemperatureofthe
atmosphere is equal to the dew point.
7. Cryogenics is the study of low temperature.
8. As RH is expressed in percentage, hence the maximum
value of RH maybe 100%.
9. The saturation vapour pressure of water at 100ºC is 760
mm ofHg at sea level.
10. As the temperature rises, the absolute humidity may
increase and the relative humiditymayremain constant or
may even decrease.
11. Ifthe relative humidityis high then at the same temperatue
one feels hotter.
12. If the air is absolutley dry, the dew point is not observed.
13. The relative humidity decreases with the increase in
temperature.
14. Ifwater is sprinkled in the room, both relative humidityas
well as the dew point increase.
15. Dew appears on the leaves of the trees etc. due to the
condensation of saturated vapours.
16. Themist or fog is thesmall droplets of water formed due to
the condensation of water vapours near the surface of
earth.
17. Mist or fog formed much higher above the surface of earth
is called cloud.
11.1](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-289-320.jpg)
![286 PHYSICS
18. The Relative humidity between 50% and 60% gives
comfortable feeling to human beings.
19. When the relative humidityis 100%, the reading of the dry
and wet bulbs is same.
20. Smaller the difference in the temperature of dry and wet
bulbs, larger is the relative humidity.
21. Water vapours are always seen around the ice, because the
temperature around it is less than the dew point.
HEAT TRANSFER
Three modes of transmission of heat :
(a)Conduction (b) Convection and(c)Radiation
(a) Conduction : In thermal conduction particles of body at
higher temperature transmit heat to the particles at lower
temperature by mutual contact (collision) only and not by
the movement of the particles. All solids are heated by
conduction. Conduction cannot take place in vacuum.
Dx
D
D
Q
t
D
D
Q
t
A
T1
T2
T > T
1 2
Figure shows a solid of cross-section area A and thickness
Dx. Thefaceareatdifferent temperatureT1 and T2 (T1 > T2)
The rate of heat flow ÷
ø
ö
ç
è
æ
D
D
t
Q
as found experimentally is
given by
÷
ø
ö
ç
è
æ
D
D
µ
D
D
x
T
A
t
Q
where 2
1 T
T
T -
=
D
Þ
Δ Δ
Δ Δ
æ ö
= ç ÷
è ø
Q T
KA
t x
…(1)
where K is proportionality constant called thermal
conductivity.
It is a measure of how quickly heat energy can conduct
through the substance.
Coefficientof thermalconductivity(K): Thecoefficientofthermal
conductivity, K, of a material is defined as the amount of heat that
flowing per second through a rod of that material having unit
length and unit area of cross-section in the steady state, when
the difference of temperature between two ends of the rod is 1 ºC
and flow of heat is perpendicular to the end faces of the rod.
Unit of coefficient of thermal conductivity in SI system is
watt/m-K
Dimensions : [M L T–3 q–1]
For a perfect conductor thermal conductivity K is infinite and
for a perfect insulator K is zero.
In general, solids are better conductors than liquids and liquids
are better conductors than gases. (Heat transfer through the
process of conduction is possible in liquids and gases also, if
theyare heated from the top.) Metals are much better conductors
than non-metals.
A good conductor of heat is also a good conductor of electricity
The conduction ofboth heat and electricityis due to the movement
of free electrons.
(b) Convection : It is the process by which heat is transferred
from one place to another in a medium by the movement of
particles of the medium. It occurs due to densitydifference.
This phenomenon occurs in fluids.
(c) Radiation : It is the process by which heat is transferred
from one place to another without any intervening medium.
The light reaches from Sun to Earth byradiation process.
Keep in Memory
1. The equation
Δ Δ
Δ Δ
æ ö
= ç ÷
è ø
Q T
KA
t x
is valid for steady state
condition. The condition is said to occur when no part of
heat is used up in raising the temperature of any part of
cross-section of the solid.
2. On comparing equation (1)with the following equation used
for flowing of charge on account of potential difference.
V1
Dq
V2
s
l
We find :
l
V
A
t
q D
s
=
D
D
The role of resistance (thermal resistance) is played by
Dx
KA
3. Series combination of conductors
l1 l2
K , A
1 1
T1 T T2
K , A
2 2
Equivalent thermal conductivity:
1 2
1 2
2
=
+
eq
K K
K
K K
1 2
1 2
1 2
( – )
A T T
H
l l
K K
=
+
where H = heat flow per second
4. Parallel combination of conductors
l
K , A
1 1
T1 T2
K , A
2 2
Equivalent thermal conductivity:
Keq = 1 1 2 2
2 2
+
+
K A K A
A A
1 2
1 2
1 2
1 2
1 2
K K
T + T
l l
H =
K K
+
l l](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-290-320.jpg)
![287
Thermal Properties of Matter
5. Davy’s safety lamp is based on the conduction. It is used in
mines toknow the ignition temperature of gases. Danger of
explosion can be avoided.
6. (i) Principle of chimney used in a kitchen or a factory is
based on the convection.
(ii) Land and sea breezes are due ot the convection.
(iii) Temperature of theupper part of theflameis more than
the temperature on the sides, because the currents of
air carrythe heat upwards.
(iv) Radiation can be detected by differential air
thermometer, Bolometer, thermopile, etc.
Example6.
Two plates of same area are placed in contact. Their
thickness as well as thermal conductivities are in the ratio
2 : 3. The outer surface of one plate is maintained at 10ºC
and that of other at 0ºC. What is the temp. of the common
surface?
Solution :
Let q be the temp. of common surface.
As
2
1
t
Q
t
Q
÷
÷
ø
ö
ç
ç
è
æ
D
D
=
÷
÷
ø
ö
ç
ç
è
æ
D
D
2
2
2
1
1
1
x
)
0
(
A
K
x
)
10
(
A
K
-
q
=
q
-
or 1 1
2 2
K x
(10 θ) θ
K x
- =
K1
x1 x2
K2
Plate 1 Plate 2
10°C 8°C 0°C
Now,
3
2
K
K
x
x
;
A
A
2
1
2
1
2
1 =
=
= ; .
C
º
5
or
3
2
)
10
(
3
2
=
q
q
=
q
-
Example7.
A slab consists of two parallel layers of two different
materials of same thickness and thermal conductivities
K1 and K2. Find the equivalent thermal conductivity of
the slab.
Solution :
Rate of flow of heat through each layer of slab is same,
because slabs are in series.
x
x
DT1
DT2
l
l
l 2
A
)
T
T
(
K
T
A
K
T
A
K 2
1
2
2
1
1
D
+
D
=
D
=
D
or C
2
)
T
T
(
K
T
K
T
K 2
1
2
2
1
1 =
D
+
D
=
D
=
D , say
K
C
2
T
T
,
K
C
T
,
K
C
T 2
1
2
2
1
1 =
D
+
D
=
D
=
D
or
K
C
2
K
C
K
C
2
1
=
+ or
2
1
2
1
K
K
K
K
2
K
+
=
Example8.
Two walls of thickness d1 and d2 and thermal conductivities
K1 and K2 are in contact. In the steady state, if the
temperatures at the outer surfaces are T1 and T2 then find
the temperature at the common wall.
Solution :
K1
T1 T2
T
d1 d2
K2
Let the temperature of common wall be T. Then
2
2
2
1
1
1
d
t
)
T
T
(
A
K
d
t
)
T
T
(
A
K -
=
-
or,
2
2
2
1
1
1
d
t
)
T
T
(
K
d
t
)
T
T
(
K -
=
-
or, )]
T
T
(
K
[
d
)]
T
T
(
K
[
d 2
2
1
1
1
2 -
=
-
or, 2
2
1
2
1
2
1
2
1
1 T
K
d
T
K
d
T
d
K
d
T
K -
=
-
or, ]
K
d
d
K
[
T
T
d
K
d
T
K 2
1
2
1
2
1
2
2
1
1 +
=
-
ú
û
ù
ê
ë
é
+
-
=
1
2
2
1
2
1
2
2
1
1
d
K
d
K
T
d
K
d
T
K
T
HEAT TRANSFER BY RADIATION AND NEWTON’S LAW
OF COOLING
Stefan’s Law:
This law is also called Stefan Boltzmann law. This law states that
the power radiated for overall wavelength from a black body is
proportional to the fourth power of thermodynamic temperature T.
4 4
E T E T
µ Þ = s for perfectly black body ....(1)
where E is energyemitted per second from unit sruface area of the
black body, T is temperature and s is Stefan’s constant, and
s = 5.67×10–8 Wm–2 K–4.
If body is not perfectly black body, then
E = es T4 ....(2)
where e is emissivity. Then energyradiated per second by a body
of area A is
E1 = es T4 ....(3)
If the body temperature is T and surrounding temperature is T0,
then net rate of loss of energy by body through radiation from
equation (3) is
' 4 4
1 0
( )
E eA T T
= s - ....(4)
Now rate of loss of energy in terms of specific heat c is
'
1
dQ dT
mc E
dt dt
= = ....(5)
and 4 4
0
( )
dT eA
T T
dt mc
s
= - ....(6)
(T- temperature, t - time in second)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-291-320.jpg)
![288 PHYSICS
So body cools by radiation and rate of cooling depends on
e (emissivity of body), A (area of cross-section of body),
m (mass of body) and c (specific heat capacity of body).
A black body is defined as a body which completely absorbs all
the heat radiation falling on it without reflecting and
transmitting any of it.
Weins Law :
lmT = b,
where b is the Weins constant and b = 2.898 × 10–3mK
and T = temperature.
Graphof lm versus T
T
2
1
1
2
l
=
l
m
m
T
T
Hence on increasing temperature of a body, its colour changes
gradually from red to orange ® yellow ® green ® blue ®
violet. Thus the temperature of violet star is maximum and
temperature of red star is minimum. Sun is a medium categorystar
with lm = 4753Aº (yellow colour) and temperature6000K.
Kirchoff’s Law
According to this law, the ratio of emissive power to absorptive
power is same for all surfaces at the same temperature and is
equal to the emissive power of a perfectly black body at the same
temperature.
i.e.
e
E A
a
=
where e = emissive power of a given surface
a = absorptive power of a given surface
E = emissive power of a perfect black body
A = absorptive power of a perfect black body
(i) For a perfect black body, A = 1, =
e
E
a
(ii) If emissive and absorptive power are considered for a
particular wavelenth l then l
l
l
=
e
E
a
(iii) SinceEl is constant at a given temperature, according to
this law if a surface is good absorber of a particular
wavelength then it is also a good emitter of that wavelength.
Fraunhoffer's Line
(i) Fraunhoffer lines are the dark lines in the spectrum of sun
and are explained on the basis ofKirchoff’s law. When white
light emitted from central core of sun (photosphere) passes
through its atmosphere (chromosphere) radiation of those
wavelength will be absorbed by the gases present there,
which theyusuallyemit (as good emitter is a good absorber)
resulting dark lines in the spectrum of sun.
(ii) On the basis ofKirchoff’s law, Fraunhoffer identified some
of the elements present in the chromosphere. They are
hydrogen, helium, sodium, iron, calcium, etc. Fraunhoffer
had observed about 600 darklines in the spectrum of sun.
Newton's Law of Cooling
The rate of loss of heat of a body is directly proportional to the
temperature difference between the body and the surroundings.
i.e. 0
( )
dT
K T T
dt
= - -
where T = temperature of body, T0 = temperature ofsurrounding.
and
mc
eA
K
s
= where, e = emissivity of body, A = area of surface
of body, s = Stefan’s constant, m = mass ofbody, c = specific heat
of body.
It is a special case of Stefan’s lawand above relation is applicable
onlywhen the temperature ofbody is not much different from the
temperature of surroundings.
Solar constant : Solar constant is the solar radiation incident
normally per second on one square metre at the mean distance
of the earth from the sun in free space.
It is given byS = 1.34 × 109 Jm–2s–1.
Temperature of sun is given T4 = S/s(R/r)2, where R is mean
distance of the earth from the sun and r is the radius of the sun.
Keep in Memory
1. Good absorber is a good emitter.
2. Cooking utensils are provided with wooden or ebonite
handles, since wood or ebonite is a bad conductor of heat.
3. Good conductor of heat are good conductors of electricity,
Mica is an exception which being a good conductor ofheat
is a bad conductor of electricity.
Example9.
Compare the rate of loss of heat from a metal sphere of
temperature 827°C, with the rate of loss of heat from the
same sphere at 427 °C, if the temperature of surroundings
is 27°C.
Solution :
Given : T1 = 827 °C = 1100 K, T2 = 427 °C = 700 K
and T0 = 27 °C = 300 K
According to Steafan Boltzmann law ofradiation,
dQ
dt
= s A
Ae (T4 – T0
4)
4 4 4 4
1 0
1
4 4 4 4
2 0
2
dQ
dt (T T ) [(1100) (300) ]
dQ (T T ) [(700) (300) ]
dt
æ ö
ç ÷
è ø - -
= =
æ ö - -
ç ÷
è ø
=6.276
or
1 2
dQ dQ
: 6.276 :1
dt dt
æ ö æ ö
=
ç ÷ ç ÷
è ø è ø
Example10.
The filament of an evacuated light bulb has a length 10 cm,
diameter 0.2 mm and emissivity 0.2, calculate the power it
radiates at 2000 K. (s = 5.67 × 10–8 W/m2 K4)
Solution :
l= 10cm= 0.1 m, d= 0.2mm =2 × 10–4 m
r = 0.1mm=1×10–4 m,
e = 0.2, T = 2000 K, s= 5.67 ×10–8 W/m2 K4
According to stefan's law of radiation, rate of emission of
heat for an ordinary body,
E = sAeT4 = s(2 pr l) eT4 [QA= 2prl]
= 5.67 ×10–8 × 2× 3.14 ×1 ×10–4 × 0.1 × 0.2 × (2000)4
= 11.4 W
Power radiated bythe filament = 11.4 W](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-292-320.jpg)






![295
Thermal Properties of Matter
Exemplar Questions
1. A bimetallic strip is made of aluminium and steel (aAl >
asteel). On heating, the strip will
(a) remain straight
(b) get twisted
(c) will bend with aluminium on concave side
(d) will bend with steel on concave side
2. A uniform metallic rod rotates about its perpendicular
bisector with constant angular speed. Ifit isheated uniformly
to raise its temperature slightly
(a) its speed of rotation increases
(b) its speed of rotation decreases
(c) its speed of rotation remains same
(d) its speed increases because its moment of inertia
increases
3. The graph between two temperature scales A and B isshown
in figure between upper fixed point and lower fixed point
there are 150 equal division on scale A and 100 on scale B.
The relationship for conversion between the two scales is
given by
O 100
180
DtB = 100°
DtA = 150°
Temperature (°B)
Temperature
(°A)
(a)
180
100 150
A B
t t
-
= (b)
30
150 100
A B
t t
-
=
(c)
180
150 100
B A
t t
-
= (d)
40
100 180
B A
t t
-
=
4. An aluminium sphere is dipped into water. Which of the
following is true?
(a) Buoyancywill beless in water at 0°C than that in water
at4°C
(b) Buoyancywill bemorein water at 0°C than that in water
at4°C
(c) Buoyancyin water at 0°C will be same as that in water
at4°C
(d) Buoyancymaybemoreor less in water at 4°Cdepending
on the radius of the sphere
5. As the temperature is increased, the period of a pendulum
(a) increases as its effective length increases even though
its centre of mass still remains at the centre of the bob
(b) decreases as its effective length increases even though
its centre of mass still remains at the centre of the bob
(c) increases as its effectivelength increases due toshifting
to centre of mass below the centre of the bob
(d) decreases as its effective length remains same but the
centre of mass shifts above the centre of the bob
6. Heat is associated with
(a) kinetic energy of random motion of molecules
(b) kinetic energy of orderlymotion of molecules
(c) total kinetic energy of random and orderly motion of
molecules
(d) kinetic energy of random motion in some cases and
kinetic energy of orderlymotion in other
7. The radius ofa metal sphere at room temperature T is R and
the coefficient of linear expansion of the metal is a. The
sphere heated a little by a temperature DT so that its new
temperature is T + DT. The increase in the volume of the
sphere is approximately.
(a) 2 R T
p aD (b) 2
R T
p aD
(c) 3
4 / 3
R T
p aD (d) 3
4 R T
p aD
8. Asphere, a cubeanda thin circular plate, all of samematerial
andsame mass are initiallyheatedtosame high temperature.
(a) Plate will cool fastest and cube the slowest
(b) Sphere will cool fastest and cube the slowest
(c) Plate will cool fastest and sphere the slowest
(d) Cube will cool fastest and plate the slowest
PastYears (2013-2017) NEET/AIPMTQuestions
9. A piece of iron is heated in a flame. It first becomes dull red
then becomes reddish yellow and finallyturns to white hot.
The correct explanation for the above observation is
possible by using [2013]
(a) Wien’s displacement law
(b) Kirchoff’s law
(c) Newton’s law of cooling
(d) Stefan’s law
10. The density of water at 20°C is 998 kg/m3 and at 40°C 992
kg/m3. The coefficient of volume expansion of water is
[NEET Kar. 2013]
(a) 10–4/°C (b) 3 × 10–4/°C
(c) 2 × 10–4/°C (d) 6 × 10–4/°C](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-299-320.jpg)
![296 PHYSICS
11. Two metal rods 1 and 2 of same lengths have same
temperature difference between their ends. Their thermal
conductivitiesareK1 and K2 and cross sectional areas A1
and A2, respectively. If the rate of heat conduction in rod 1
is four times that in rod 2, then [NEET Kar. 2013]
(a) K1A1 = K2A2 (b) K1A1 = 4K2A2
(c) K1A1 = 2K2A2 (d) 4K1A1 = K2A2
12. Certain quantityofwater cools from 70°Cto60°C in the first
5minutes and to54°C in thenext5minutes. Thetemperature
of the surroundings is: [2014]
(a) 45°C (b) 20°C
(c) 42°C (d) 10°C
13. Steam at 100°C is passed into 20 g of water at 10°C. When
water acquires a temperature of 80°C, the mass of water
present will be: [2014]
[Take specific heat ofwater = 1 cal g– 1 °C– 1 and latent heat
of steam = 540 cal g– 1]
(a) 24 g (b) 31.5g
(c) 42.5g (d) 22.5g
14. On observing light from three different stars P, Q and R, it
was found that intensityof violet colour is maximum in the
spectrum of P, the intensity of green colour is maximum in
thespectrum of Rand the intensityof red colour ismaximum
in the spectrum of Q. If TP, TQ and TR are the respective
absolute temperature ofP, Q and R, then it can beconcluded
from the above observations that [2015]
(a) TP > TR > TQ (b) TP < TR < TQ
(c) TP < TQ < TR (d) TP > TQ > TR
15. The two ends of a metal rod are maintained at temperatures
100°C and 110°C. The rate of heat flowin the rod is found to
be 4.0 J/s. If the ends are maintained at temperatures 200°C
and 210°C, the rate of heat flow will be [2015]
(a) 16.8 J/s (b) 8.0 J/s
(c) 4.0 J/s (d) 44.0 J/s
16. The value of coefficient of volume expansion of glycerine is
5 × 10-4 K-1. Thefractional changein thedensityofglycerine
for a rise of 40°C in its temperature, is: [2015 RS]
(a) 0.020 (b) 0.025
(c) 0.010 (d) 0.015
17. Apiece of ice falls from a height h sothat it melts completely.
Only one-quarter of the heat produced is absorbed by the
ice and all energy of ice gets converted into heat during its
fall. The value ofh is : [2016]
[Latent heat ofice is 3.4 × 105 J/kg and g = 10 N/kg]
(a) 34km (b) 544km
(c) 136km (d) 68km
18. Coefficient of linear expansion of brass and steel rods are
a1 and a2. Lengths of brass and steel rods are 1
l and 2
l
respectively. If 2 1
( )
l l
- is maintained same at all
temperatures, which one of the following relations holds
good ? [2016]
(a) 2 2
1 2 2 1
l l
a =a (b) 1 2 2 1
l l
a =a
(c) 1 2 2 1
l l
a =a (d) 1 1 2 2
a = a
l l
19. A black body is at a temperature of 5760 K. The energy of
radiation emitted by the body at wavelength 250 nm is U1,
at wavelength 500 nm is U2 and that at 1000nmisU3.Wien's
constant, b = 2.88 × 106 nmK. Which of the following is
correct ? [2016]
(a) U1 = 0 (b) U3 = 0
(c) U1 > U2 (d) U2 > U1
20. A spherical black body with a radius of 12 cm radiates 450
watt power at 500 K. If the radius were halved and the
temperature doubled, the power radiated in watt would be :
(a) 450 (b) 1000 [2017]
(c) 1800 (d) 225
21. Two rods Aand B of different materials are welded together
as shown in figure. Their thermal conductivities are K1 and
K2. The thermal conductivityof the composite rod will be :
A K1
B K2
T1 T2
d
[2017]
(a)
1 2
3(K K )
2
+
(b) K1 + K2
(c) 2 (K1 + K2) (d) 1 2
K K
2
+](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-300-320.jpg)
![297
Thermal Properties of Matter
EXERCISE - 1
1. (c) 2. (d) 3. (d) 4. (c) 5. (b)
6. (c) 7. (a) 8. (d)
9. (a)
strain
stress
/
A
/
F
E =
D
=
l
l
where Dl=(l'–l) = lat so F = EAat
10. (a) 11. (c)
12. (b) Let the angle subtended by the arc formed be q. Then
2
1
1
2
r
r
r
or
r -
-
=
D
D
=
q
=
q
l
l
l
l
t
T
)
( 1
2 D
a
-
a
=
q
l
t
T
)
(
r
or 1
2 D
a
-
a
=
l
l
So,
T
)
(
t
r
1
2 D
a
-
a
=
13. (a) Initial rate of loss of heat
2
2
2
1
2
4
1
4
R
R
e
A
T
e
A
T
=
´
´
s
´
´
s
=
14. (b) Momentum of photon
E
c
=
Change in momentum
2E
c
=
= momentum transferred to the surface
(the photon will reflect with same magnitude of
momentum in opposite direction).
15. (c) We know
4
eT
E = T
ln
4
e
ln
E
ln +
=
Þ
negative
is
e
ln
1
e
because <
E
ln
T
ln
16. (c) The temperature is measured by the value of the
thermodynamic property of a substance i.e., the
propertywhich varies linearlywith the temperature.
17. (b) Temperature of stars can be determined by Wein’s
displacement law
=
lm constant
18. (c)
19. (b) We know that Q =
T T
R
H L
-
Also Thermal resistance, R=
l l
KA K r
=
p
2
Heat flowwill be maximum when thermal resistance is
minimum. From given option
(i) r = 2r0, l = 2l0
= =
R
K r K r
2
2 2
0
0
2
0
0
2
l l
p p
( )
(ii) r = 2r0, l = l0
= =
R
K r K r
l l
0
0
2
0
0
2
2 4
p p
( )
(iii) r = r0, l = 2l0
= =
R
K r K r
2 2
0
0
2
0
0
2
l l
p p
(iv) r = r0, l = l0
= =
R
K r K r
l l
0
0
2
0
0
2
p p
It is clear that for option (b) resistance is minimum,
hence heat flowwill bemaximum.
20. (c)
21. (a) In condition of weightlessness, convection is not
possible.
22. (a) eff 1 2
r r r
=
2 1 1 2 2 1
KA(T T ) K r r (T T )
dQ
dt L L
- p -
= =
23. (c) When a body is heated then relation between colours
and temperature is according to Prevost’s theory of
radiation which states that everybody emitting radiant
energyin all directions at a rate depending only on the
nature of its surface and its temperature e.g., when a
bodyis placed in an enclosure(furnace) it would acquire
the temperature of furnace and seem white means
radiate white light. So it becomes first dark and then
white.
24. (c) 1 2
kA (T T )
dQ
dt L
-
=
[(T1–T2) is the temperature difference]
25. (b)
EXERCISE - 2
1. (c) )
t
1
(
R
R 0
t a
+
=
)
10
1
(
R
71
.
2 0 ´
a
+
= ...(1)
)
100
1
(
R
70
.
3 0 ´
a
+
= ...(2)
)
t
1
(
R
26
.
3 0 a
+
= ...(3)
Solve these equations to obtain the value of t.
2. (a)
5
C
9
32
140
=
-
or C
9
160
700
=
-
or C = 60ºC
3. (c) t
T
2
1
t ´
D
a
=
D
Hints & Solutions](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-301-320.jpg)
![298 PHYSICS
86400
)
15
T
(
2
1
5 ´
-
a
=
and 86400
)
T
30
(
2
1
10 ´
-
a
=
4. (a) a
µ
a
= F
or
A
t
Y
F
(Q Y t A is same for both copper and iron)
or C C Ι Ι
F α and F α
µ µ
2
3
1
2
/
3
F
FC
=
=
I
5. (b)
Δ
αΔT
=
l
l
5 3
10 100 10
- -
= ´ =
3
Δ
100% 10 100
-
´ = ´
l
l
1
10 0.1%
-
= =
6. (a) Let m be the mass of steam condensed. Then
m×540+m×10/2=22 ×70
m= 2.83gm
Now, total mass = 22 + 2.83 = 24.83 gm
7. (d) Thermal resistance R =l/KA
Where l =20cm. & A(cylindrical rod)
=pr2 =40pcm2
So = =
´ p ´
20 cal
R 0.318
0.5 40 sec º C
8. (c) According to Stefan’s Law, the rate of loss of heat is
e
)
T
T
(
A
t
Q 4
2
4
1 ´
-
s
=
here s = 5.67 × 10–8J/m2 × sec.K2,
T1=527+273=800K,
T2 = 27+ 273 = 300K& A= 200×10–4m2
So. 8 2
4 4
Q
5.67 10 2 10
t
[(800) (300) ] 0.4
- -
= ´ ´ ´
- ´
@ 182 joule
9. (a) According to Stefan’s Law
energy radiated per sec E = sAT4
(here e = 1 for black body)
for first case E = sA(273)4
for second case E1=sA(546)4 so E1=16E
10. (b) According to Wein's displacement law, λ T = b.
m
where b=2.884 × 10–3 mK.
So l = l
m m
1 2
1 2
T T
or 4800 × 6000 = l ´
m2
3000 or l = °
m2
9600A
11. (b) The time of cooling increases as the difference between
the temperature of body& surrounding is reduced. So
T1 < T2 < T3 (according to Newton’s Law of cooling).
12. (c) 5 5
1 2
11.0 10 T 5.5 10 T
- -
´ = ´
2
1
T
T
2
1
=
13. (c)
14. (c)
5
80
9
32
F
=
-
F – 32 = 144 or F = 176ºF.
15. (d) Percentage change in volume = gt × 100
t
300
100
t
3 a
=
´
a
= 2
.
1
200
10
2
300 5
=
´
´
´
= -
16. (b)
17. (c) According to Stefan's Boltzmann law, the energy
radiated per unit time E = sAT4.
5.67 × 104 = 5.67 × 10–8 × 1 × T4 ( A = 1 m2)
or,
1/ 4
4
–8
5.67 10
T 1000K
5.67 10
æ ö
´
= =
ç ÷
´
è ø
or , T = 1000 – 273 = 727°C.
18. (a) When the temperature of cold junction is increased,
the neutral temperature remains constant for a given
thermocouple and it is independent of the temperature
of the cold junction.
qn = 275°C, qi – qn = qn – qc
qi = 2qn – qc = 530°C.
19. (a) According to Newton's law of cooling,
1 2 1 2
0
K
t 2
q - q q + q
é ù
= - q
ê ú
ë û
where q0 is the surrounding temperature.
60 40 60 40
K 10
7 2
- +
æ ö
= -
ç ÷
è ø
Þ
20
40K
7
= Þ
1
K
14
=
40 28 40 28
K 10
t 2
- +
é ù
= -
ê ú
ë û
Þ
12
24K
t
=
or
12 12 14
t 7min
24K 24
´
= = =
20. (a) Let q be temperature of interface.
Q
P
K A( 0)
K A(100 ) q -
- q
=
l l
P
Q
K
K 100
q
=
- q Þ
2
3 100
q
=
-q
or, 200 – 2q = 3q or, 5q= 200 or, q = 40°C
21. (a) Let the final temperature of mixture be T.
Then 100 × 80 + 100 (T – 0) ×½
(as specific heat of ice is 0.5 cal/g C° and specific heat
ofwater is 1 cal/gC°)
= 100 × 1 ×(100 – T)
Solving, we get T = 13.33ºC.
22. (a) 3
2
1 a
+
a
+
a
=
g
7
7
7
10
231
10
231
10
13 -
-
-
´
+
´
+
´
=
7
10
475 -
´
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-302-320.jpg)
![299
Thermal Properties of Matter
23. (a) T
)
(
V
V g
m
0 D
g
-
g
=
D
100
)]
10
10
(
3
10
82
.
1
[
1 6
4 -
-
´
´
-
´
=
100
)]
10
3
.
0
10
82
.
1
[
1 4
4 -
-
´
-
´
= =15.2ml
24. (c) Given Δ / 0.10% 0.001 and ΔT 100º C
= = =
l l
Now
Δ
αΔT
=
l
l
or 0.001 α 100
= ´
or 5
α 10 /º C
-
=
Further 5
γ 3α 3 10 /ºC
-
= = ´
3
Δ V
100 (3 10 ) (100) 0.30%
V
-
´ = ´ =
25. (a) We know that real apparent vessel
γ γ γ
= +
So, app vessel glass app vessel steel
(γ γ ) (γ γ )
+ = +
(Q real
g is same in both cases)
or 6
vessel glass
153 10 (γ )
-
´ +
steel
vessel
6
)
(
10
144 g
+
´
= -
Further vessel steel
(γ )
6 6
3 3 (12 10 ) 36 10 /ºC
- -
= a = ´ ´ = ´
6
vessel glass
153 10 (γ )
-
´ +
6
6
10
36
10
144 -
-
´
+
´
=
Solving we get 6
vessel glass
( ) 27 10 /ºC
-
g = ´
or
glass 6
9 10 /ºC
3
-
g
a = = ´
26. (b) Let the final temperature be T.
Then 200 × 1 × (T – 20)+ 20× (T– 20)
= 440 (92 – T)
Solving it, we get T = 68ºC.
27. (a) )
80
100
(
m
mL -
+
)
15
80
(
02
.
0
)
15
–
80
(
1
1
.
1 -
´
+
´
´
=
30
.
1
5
.
71
m
20
540
m +
=
+
´
80
.
72
m
560 = 130
.
0
m =
28. (d) h
mg
mgh
W
W
W 2
1 ¢
-
=
-
= )
h
h
(
mg ¢
-
=
8
.
19
10
5
)
2
.
0
20
(
10
5 ´
´
=
-
´
=
joule
990
198
5 =
´
=
This energyis converted intoheat when the ball strikes
the earth. Heat produced is
calorie
2
.
4
990
Q =
C
º
32
11
09
.
0
5000
42
100
99
mc
Q
T =
´
´
´
=
=
D
29. (b) 80× 1 × 30= m × 80 Þ m = 30gm.
30. (c)
31. (a) Use 2
2
2
1
2
1
K
K
l
l
=
32. (b) Here flow of heat, area of vessels & temperature
gradient are same so
1 1 2 2
dT dT
Q K A t K A t
dx dx
= =
so
4
7
20
35
t
t
K
K
1
2
2
1
=
=
=
33. (b)
34. (b) 1 1 2 2
λ T λ T
=
2
T
.
9506
4753
6050 =
´
K
3025
T2 =
35. (a)
)
T
T
(
)
T
T
(
E
E
4
0
4
2
4
0
4
1
2
1
-
s
-
s
=
4
4
4
4
)
300
(
)
500
(
)
300
(
)
600
(
-
-
=
36. (d) Thermal capacity= 40 × 0.2 = 8 cal °C–1
37. (b) –13°F is (13 + 32)° below ice point on F scale.
38 (a) Mass ratio 1 : 2; hence DT ratio 2 : 1. Therefore
equilibriumtemp is30°C.
39. (b) Heat capacityof cold : hot =1 : 2
Sofinal temp. is
3
1
× (2 × 92 + 1 × 20) = 68°C.
40. (d) 4
T
area
E ´
´
s
= ; T increases by a factor
2
3
.
Area increases by a factor
4
1
.
41. (d)
2
t , t '
A A / 2
µ µ
l l
42. (a) q
=
q
-
Þ
-
q
=
q
- 4
400
)
0
(
K
)
100
(
K
4
80 C
Þ q = °
43. (a) 540 ×80 +540q = 540 (80–q)
°
=
q
Þ
=
q
Þ
q
-
=
q
+
Þ 0
0
2
80
80
44. (a)
45. (c) The total power radiated by a black body of area A at
temperature TK is given byP = AsT4
Where s = Stefan's constant
= 5.7 × 10–8 W m–2 K–4
Which is best represented in graph. (c)
46. (b) According to Stefan’s law 4
E T ,
= s
T1 = 500K
T2 = 1000 K
4 4
2 2
1 1
E T 1000
16
E T 500
æ ö æ ö
= = =
ç ÷
ç ÷ è ø
è ø
E2 = 16 × 7 = 112 cal / cm2s
47. (a) The rate of heat loss per unit area due to radiation
= Îs (T4–T0
4)
= 0.6 × 5.67 × 10–8 [(400)4–(300)4] = 595 Jm–2s–1.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-303-320.jpg)

![301
Thermal Properties of Matter
5. (a) As the temperature increased the length (L) of the
pendulum increases due to expansion i.e., linear.
Pendulum
L
So, Time period of pendulum
2
L
T
g
= p
T L
µ
Hence on increasing temperature, time period (T) also
increases.
6. (a) As we know that when the temperature increases
vibration of molecules about their mean position
increases hence the kinetic energy associated with
random motion of molecules increases.
7. (d) Let the radius of the sphere is R. As the temperature
increases radius of the sphere increases as shown.
R
dV
Original volume
3
4
3
V R
= p
Coefficient of linear expansion = a
Coefficient of volume expansion = 3a
As we know that
V
Y
V t
D
=
D
By putting the value of V, increase in the volume
3
V V t
Þ D = aD 3
4 R t
= p aD
8. (c) Loss of heat temperature on cooling temperature
increase depend on material of object surface area
exposed to surrounding and temperature difference
between body and surrounding.
Let us consider the diagram where all the three objects
are heated to same temperature T. As we know that
density
mass
volume
r =
where r is same for all the three objects hence, volume
will also be same.
m
T
Plate
Cube
Sphere
T
T
m
m
As thickness of the plate is least so, surface area of the
plateismaximum.
We know that, according to Stefan's law of heat loss
4
H AT
µ
where, A is surface area of object and T is temperature.
So, Hsphere : Hcube : Hplate
= Asphere : Acube : Aplate
Soarea ofcircular plate ismaximum.
For sphere, as the sphere is having minimum surface
area.
Hence, the sphere cools slowest and circular platewill
cool faster.
PastYears (2013-2017) NEET/AIPMTQuestions
9. (a) Wein’s displacement law
According to this law
lmax µ
1
T
or, lmax × T = constant
So, as the temperature increases l decreases.
10. (b) From question,
Dr = (998– 992) kg/m3 = 6 kg/m3
r =
3 3
998 992
kg/m 995 kg/m
2
+
=
r =
m
V
Þ
V
V
Dr D
= -
r
Þ
V
V
Dr D
=
r
Coefficient of volume expansion of water,
1 1
V
V t t
D Dr
=
D r D
=
4
6
3 10 / C
995 20
-
» ´ °
´
11. (b) Q1 = 4Q2 (Given)
Þ 1 1 2 2
4
K A t K A t
L L
D D
= Þ K1A1 = 4K2A2.
12. (a) Let the temperature of surroundings be q0
By Newton's law of cooling
1 2 1 2
0
k
t 2
q - q q + q
é ù
= - q
ê ú
ë û
Þ 0
70 60 70 60
k
5 2
- +
é ù
= - q
ê ú
ë û
Þ 2 = k [65 – q0] ...(i)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-305-320.jpg)
![302 PHYSICS
Similarly, 0
60 54 60 54
k
5 2
- +
é ù
= - q
ê ú
ë û
Þ
6
5
= k [57 – q0] ...(ii)
Bydividing (i) by(ii) we have
0
0
65
10
6 57
- q
=
- q
Þ q0 = 45º
13. (d) According to the principle of calorimetry.
Heat lost = Heat gained
mLv + mswDq = mwswDq
Þ m×540+m×1×(100–80)
=20 ×1×(80 –10)
Þ m= 2.5g
Therefore total mass of water at 80°C
=(20 +2.5) g= 22.5g
14. (a) From Wein’s displacement law
lm × T = constant
P – max. intensityis at violet
Þlm isminimumÞtempmaximum
R – max. intensityis at green
Þ lm is moderate Þ temp moderate
Q – max. intensityis at red Þ lm is maximum Þtemp.
minimum i.e., Tp > TR > TQ
15. (c) As the temperature difference DT = 10°C as well as the
thermal resistance is same for both the cases, sothermal
current or rate of heat flow will also be same for both
the cases.
16. (a) From question,
Rise in temperature Dt = 40°C
Fractional change in the density
0
Dr
r
= ?
Coefficient of volume expansion
g = 5 × 10–4K–1
r = r0 (1 –gDt)
Þ
0
Dr
r
= gDT = (5 ×10–4) (40) = 0.02
17. (c) According to question only one-quarter of the heat
produced by falling piece of ice is absorbed in the
meltingof ice.
i.e.,
mgh
4
=mL
Þ h =
5
4L 4 3.4 10
136 km
g 10
´ ´
= = .
18. (d) From question, (l2 – l1) is maintained same at all
temperatures hence change in length for both rods
should be same
i.e., Dl1 = Dl2
As we know, coefficient of linear expansion,
a =
0 T
D
D
l
l
l1a1DT = l2a2DT
l1a1 = l2a2
19. (d) Accordingtowein'sdisplacementlaw, maximum amount
of emitted radiation corresponding to lm =
b
T
lm =
6
2.88 10 nmK
5760K
´
= 500 nm
U2
U
Emitted
(radiation)
250 nm
500 nm
1000 nm
wave length K
From the graph U1 < U2 > U3
20. (c) Given r1 = 12 cm, r2 =6 cm
T1 = 500 K and T2 = 2 × 500 = 1000 K
P1 = 450 watt
Rate of power loss 2 4
P r T
µ
2 4
1 1 1
2 4
2 2 2
P r T
P r T
=
2 4
2 2
2 1 2 4
1 1
r T
P P
r T
=
Solving we get, P2 = 1800 watt
21. (d) Heat current H = H1 + H2
= 1 1 2 2 1 2
K A(T T ) K A(T T )
d d
- -
+
EQ 1 2 1 2
1 2
K 2A(T T ) A(T T )
[K K ]
d d
- -
= +
Hence equivalent thermal conductivities for two rods
of equal area is given by 1 2
2
EQ
k k
K
+
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-306-320.jpg)



![308 PHYSICS
Example4.
When a system is taken from state a to state b, in fig. along
the path a ® c ® b, 60 J of heat flow into the system, and
30 J of work are done :
(i) How much heat flows into the system along the path
a ® d ® b if the work is 10 J.
(ii) When the system is returned from b to a along the
curved path, the work done by the system is –20 J.
Does the system absorb or liberate heat, and how
much?
(iii) If, Ua = 0 and Ud = 22 J, find the heat absorbed in the
process a ® d and d ® b.
P
V
c
a
b
d
Solution :
For the path a ® c ® b
dU = dQ – dW = 60 – 30 = 30 J or Ub – Ua = 30 J
(i) Along the path a ® d ® b
dQ = dU+ dW = 30 + 10 = 40 J
(ii) Along the curved path b – a
dQ = (Ua – Ub) + W = (–30) + (–20) = –50 J,
heat flows out the system
(iii) Qad = 32 J; Qdb = 8 J
Example5.
Two samples of a gas initially at same temperature and
pressure are compressed from avolume V to V/2. One sample
is compressed isothermally and the other adiabatically. In
which sample is the pressure greater?
Solution :
Let initial volume, V1 = Vand final volume, V2 = V/2
Initial pressure, P1 = P ; final pressure, P2 = ?
For isothermal compression
P2V2 = P1V1 or 1 1
2
2
P V PV
P 2P
V V / 2
= = =
For adiabatic compression
P2' V2
g = P1V1
g or P2' = P1
1
2
V
V
g
æ ö
ç ÷
è ø
=
V
P
V / 2
g
æ ö
ç ÷
è ø
or P2´ = 2gP
Since g > 1 2g > 2 P2' > P2
Pressure during adiabatic compression is greater than the
pressure during isothermal compression.
Example6.
A Carnot engine working between 300 K and 600 K has a
work output of 800 J per cycle. What is the amount of heat
energy supplied to the engine from source per cycle?
Solution :
W = 800 J, T1 = 600 K, T2 = 300 K
h = 1 – 1
2 1
T W
T Q
= =
1
300 800
1
600 Q
- = or 0.5 =
1
800
Q
Heat energy supplied by source,
800
Q
0.5
= = 1600 joule per cycle
Example7.
The temperatures T1 and T2 of the two heat reservoirs in
an ideal Carnot engine are 1500°C and 500°C respectively.
Which of the following : increasing T1 by 100°C or
decreasing T2 by 100°C would result in a greater
improvement in the efficiency of the engine?
Solution :
The efficiency of a Carnot's engine is given by 2
1
T
1
T
h = -
Given T1 =1500°C =1500+ 273= 1773Kand
T2 = 500°C = 500 + 273 = 773 K.
When the temperature of the source is increased by100°C,
keeping T2 unchanged, the new temperature of the source
is
T´1 =1500+100=1600°C =1873K.Theefficiencybecomes
2
1
T 773
´ 1 1 0.59
T´ 1873
h = - = - =
On the other hand, if the temperature ofthe sink isdecreased
by 100°C, keeping T1 unchanged, the new temperature of
the sink is T´2 = 500 – 100 = 400°C = 673 K. The efficiency
now becomes
2
1
T´ 673
´´ 1 1 0.62
T 1773
h = - = - =
Since h´´ is greater than h´, decreasing the temperature of
the sink by 100°C results in a greater efficiency than
increasing the temperature of the source by100°C.
Example8.
Calculate the work done when 1 mole of a perfect gas is
compressed adiabatically. The initial pressure and volume
of the gas are 105 N/m2 and 6 litre respectively. The final
volume of the gas is 2 litres. Molar specific heat of the gas
at constant volume is 3R/2. [(3)5/3 = 6.19]
Solution :
For an adiabatic change PVg = constant
P1V1
g = P2V2
g](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-312-320.jpg)
![309
Thermodynamics
As molar specific heat of gas at constant volume
v
3
C R
2
=
CP = CV + R =
3 5
R R R
2 2
+ = ;
P
V
C (5 / 2) R 5
C (3/ 2) R 3
g = = =
From eqn. (1) 1
2 1
2
V
P P
V
g
æ ö
= ç ÷
è ø
=
5/3
5 2
6
10 N / m
2
æ ö
´
ç ÷
è ø
= (3)5/3 × 105 = 6.19 ×105 N/m2
Work done =
5 3 5 3
1
[6.19 10 2 10 10 6 10 ]
5
1
3
- - -
´ ´ ´ - ´ ´
æ ö
- ç ÷
è ø
2
2 10 3
(6.19 3)
2
é ù
´ ´
= - -
ê ú
ê ú
ë û
= – 3 × 102 × 3.19 = – 957 joule
[–ve sign shows external work done on the gas]
Example9.
A refrigerator is to maintain eatables kept inside at 90C. If
room temperature is 360C, calculate the coefficient of
performance.
Solution :
Here, T1 =36°C =36 +273= 309K,
T2 =10°C =10 +273 =283K
2
1 2
T 283 283
COP 10.9
T T 309 283 26
= = = =
- -
Example10.
One mole of an ideal gas at pressure P0 and temperature
T0 is expanded isothermally to twice its volume and then
compressed at constant pressure to (V0/2) and the gas is
brought back to original state by a process in which P µ V
(Pressure is directly proportional to volume). The correct
representation of process is
(a)
V
P
V /2
0 V0 2V0
P0 (b)
V
P
V /2
0 V0 2V0
P0
(c)
P0
T
P
P0/2
T0
T /4
0
(d)
T
V
T0
V /2
0
V0
Solution : (c)
ProcessAB is isothermal expansion,
BC is isobaric compression and in process CA
2
nRT
P P T
P
µ Þ µ
P0
A
P
P0/2
T0
T /4
0
B
C
Example11.
A Carnot’s heat engine works with an ideal monatomic
gas, and an adiabatic expansion ratio 2. Determine its
efficiency.
Solution :
Given,
3
2
V
2
V
r = = and g for a monatomicgas = 5/3.
Using,
1
1
1
g -
æ ö
h = -ç ÷
r
è ø
we have, the required efficiency
5
1
3
1
1 1 0.63 0.37 or 37%
2
-
æ ö
h = - = - =
ç ÷
è ø](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-313-320.jpg)






![317
Thermodynamics
6. Three copper blocks of masses M1, M2 and M3 kg
respectivelyare brought intothermal contact till theyreach
equilibrium. Before contact, theywere at T1, T2, T3 (T1 > T2
> T3). Assuming there is no heat loss to the surroundings,
theequilibrium temperature Tis (s is specific heatofcopper)
(a) 1 2 3
3
T T T
T
+ +
=
(b) 1 1 2 2 3 3
1 2 3
M T M T M T
T
M M M
+ +
=
+ +
(c) 1 1 2 2 3 3
1 2 3
3( )
M T M T M T
T
M M M
+ +
=
+ +
(d) 1 1 2 2 3 3
1 2 3
M T s M T s M T s
T
M M M
+ +
=
+ +
NEET/AIPMT (2013-2017) Questions
7. A gas is taken through the cycle A ® B® C ® A, as
shown in figure. What is the net work done by the gas ?
P (10 Pa)
5
V (10 m )
3 3
A
B
C
7
6
5
4
3
2
1
0 2 6
4 8
[2013]
(a) 1000J (b) zero
(c) – 2000 J (d) 2000J
8. During an adiabatic process, the pressure of a gas is found
to be proportional to the cube of its temperature. The ratio
of
p
v
C
C
for the gas is [2013]
(a) 2 (b)
5
3
(c)
3
2
(d)
4
3
9. A system is taken from state a to state c by two paths adc
and abc as shown in the figure. The internal energy at a is
Ua = 10 J. Along the path adc the amount of heat absorbed
dQ1 = 50 J and the work donedW1 = 20 J whereas along the
path abc the heat absorbed dQ2 = 36 J. Theamount ofwork
done along the path abc is [NEET Kar. 2013]
a b
c
d
p
V
(a) 6 J (b) 10J
(c) 12J (d) 36J
10. Which ofthe following relations does not give the equation
of an adiabatic process, where terms have their usual
meaning?
(a) PgT1–g = constant [NEET Kar. 2013]
(b) P1–g Tg = constant
(c) PVg = constant
(d) TVg–1 = constant
11. Two Carnot engines A and B are operated in series. The
engineA receives heat from the source at temperature T1
and rejects the heat to the sink at temperature T. Thesecond
engine B receives the heat at temperature T and rejects to
its sink at temperature T2. For what value of T the
efficienciesofthe two enginesare equal? [NEET Kar. 2013]
(a) 1 2
2
T T
+
(b) 1 2
2
T T
-
(c) T1T2 (d) 1 2
T T
12. Athermodynamic system undergoes cyclic processABCDA
as shown in fig. The work done by the system in the cycle
is : [2014]
(a) P0V0
(b) 2P0V0
(c) 0 0
P V
2
P C B
D
A
V0 2V0 V
P0
2P0
3P0
(d) Zero
13. A monoatomic gas at a pressure P, having a volume V
expands isothermallyto a volume2V and then adiabatically
to a volume 16V. The final pressure of the gas is :(take g =
5
3
) [2014]
(a) 64P (b) 32P
(c)
P
64
(d) 16P
14. Figure below shows two paths that may be taken by a gas
to go from a state A to a state C.
2 × 10 m 4 × 10 m
–3 3 –3 3
2×10 Pa
4
6×10 Pa
4
P B C
A
V](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-321-320.jpg)
![318 PHYSICS
In process AB, 400 J of heat is added to the system and in
process BC, 100 J of heat is added to the system. The heat
absorbed by the system in the process AC will be [2015]
(a) 500J (b) 460J
(c) 300J (d) 380J
15. A carnot engine having an efficiency of
1
10
as heat engine,
is used as a refrigerator. If the work done on the system is
10 J, the amount of energy absorbed from the reservoir at
lower temperature is :- [ 2015, 2017]
(a) 90 J (b) 99 J
(c) 100 J (d) 1 J
16. The coefficient of performance of a refrigerator is 5. If the
insidetemperatureof freezer is–20°C, then thetemperature
of the surroundings to which it rejects heat is [2015 RS]
(a) 41°C (b) 11°C
(c) 21°C (d) 31°C
17. An ideal gas is compressed to half its initial volume by
means of several processes. Which of the process results
in the maximum work done on the gas? [2015 RS]
(a) Isobaric (b) Isochoric
(c) Isothermal (d) Adiabatic
18. A gas is compressed isothermallyto half its initial volume.
Thesame gas is compressedseparatelythrough an adiabatic
process until its volume is again reduced to half. Then :
[2016]
(a) Compressing the gas isothermally will require more
work to be done.
(b) Compressing the gas through adiabatic process will
require more work to be done.
(c) Compressing the gas isothermallyor adiabaticallywill
require the same amount of work.
(d) Which of the case (whether compression through
isothermal or through adiabatic process) requires more
work will depend upon the atomicity of the gas.
19. A refrigerator worksbetween 4°C and 30°C. It is required to
remove 600 calories of heat every second in order to keep
the temperature of the refrigerated space constant. The
power required is: (Take 1 cal = 4.2 joules) [2016]
(a) 2.365W (b) 23.65W
(c) 236.5W (d) 2365W
20. Thermodynamic processes are indicated in the following
diagram : [2017]
P
i
IV
f
III
f
f
f
I
700k
500k
300k V
II
Match the following
Column-1 Column-2
P. Process I A. Adiabatic
Q. Process II B. Isobaric
R. Process III C. Isochoric
S. Process IV D. Isothermal
(a) P ® C, Q ® A, R ® D, S ® B
(b) P ® C, Q ® D, R ® B, S ® A
(c) P ® D, Q ® B, R ® A, S ® C
(d) P ® A, Q ® C, R ® D, S ® B](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-322-320.jpg)

![320 PHYSICS
W
000
,
50
273
300
273
=
-
27 50,000
cal/min
273
W
´
=
4.2 27 50,000
Joule/sec
60 273
W
P
t
´ ´
= =
´
= 346 watt = 0.346 kW
4. (d) )
10
5
.
6
10
8
(
dW
dQ
dU 5
5
´
-
´
=
-
= J
10
5
.
1 5
´
=
5
5
10
5
.
1
10
dU
dQ
dW ´
-
==
-
=
5
0.5 10 J
= - ´
– ve sign indicates that work done on the gas is
J
10
5
.
0 5
´ .
5. (c) v v
dU nC dT or 80 5 C (120 100)
= = ´ -
Cv = 4.0 joule/K
6. (b) 0 0
4/3
V
4/3 4/3
P V = P P = P 8
1 1
8
æ ö Þ
ç ÷
è ø
= 16Po
7. (c)
373
23
100
373
123
373
250
1
T
T
1
1
2 +
=
=
-
=
h
Þ
-
=
h
8. (d)
T
V
)
100
/
90
(
P
T
V
P ¢
=
or
90
10
1
90
100
P
P
+
=
=
¢
or %
1
.
11
90
10
P
P
P
=
=
-
¢
9. (d) PVg =
g
÷
ø
ö
ç
è
æ
32
V
P1
or g
= = =
1.4
1
P (32) , P (32) , P 128P
10. (c) g
-
g
g
-
g
= 1
2
2
1
1
1 P
T
P
T
11. (d) 1
T 18ºC (273 18) 291 K
= = + =
and 8
/
V
V 1
2 =
We know that 1
V
T -
g = constant
or , 1
1
1
1
2
2 V
T
V
T -
g
-
g
=
1
4
.
1
1
2
1
1
2 )
8
(
291
V
V
T
T -
-
g
´
=
÷
÷
ø
ö
ç
ç
è
æ
=
C
º
5
.
395
K
5
.
668 =
=
12. (c) T
Pµ if V is constant, where P is pressure of certain
amount of gas and T is absolute zero temperature.
13. (d) We know that efficiency of carnot engine = I
T
T
L
H
-
Also, Efficiency of Heat engine =
Work output
Heat input
1
1
- =
æ ö
Þ = -
ç ÷
è ø
L
H S
S
H
T W
T Q
TL
W Q
T
4
4
127 273
6 10 1
227 273
1.2 10 cal
+
æ ö
= ´ -
ç ÷
è ø
+
= ´
14. (a) Work done in an isothermal process is given by
2
10
1
V
W 2.3026nRTlog
V
=
Here, n = 3, R = 8.31 J mol–1 degree–1
T = 300 K, V1 =4 litre, V2 = 1litre.
Hence, W = 2.3026 × 3 × 8.31 × 300 × 10
1
log
4
=17221.15(–2log102)
=–17221.15×2×0.3010=– 10368J.
15. (c) The speed of sound in air, v T
µ
1 1
2 2
v T
v T
=
Þ
1
1 2
v (27 273)
2v T
+
=
2
1 300
2 T
=
T2 =1200 K=(1200– 273)°C=927°C
16. (b) Joule
10
]
1
1671
[
10
01
.
1
V
P
dW 6
5 -
´
-
´
=
D
=
1.01 167
cal.
4.2
40cal. nearly
´
=
=
ΔQ mL 1 540,
ΔQ ΔW ΔU
= = ´
= +
or .
cal
500
40
540
U =
-
=
D
17. (b) 2
2
1 2
T 273 13 260,
T
K
T T
= - =
=
-
1
1
260
5
T 260
or T 260 52
=
-
- =
1
2
T 312K,
T 312 273 39ºC
=
= - =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-324-320.jpg)
![321
Thermodynamics
18. (b) p
5
dQ n C dT 1 R 100
2
= = ´ ´
J
10
8
.
20
J
5
.
2077 2
´
=
=
v
dU n C dT
3
1 R 100
2
1246.5J
=
= ´ ´
=
2
dU dQ dU
8.31 10 J
= -
= ´
19. (d) Under adiabatic change
g
g
-
÷
÷
ø
ö
ç
ç
è
æ
=
1
2
1
1
2
P
P
T
T
or g
g
-
=
1
2
1
1
2 )
P
/
P
(
T
T
air
for
5
/
7
4
.
1
;
)
1
/
4
(
300
T )
5
/
7
(
)
5
/
7
(
1
2 =
=
g
=
-
or 7
/
2
2 )
4
(
300
T -
=
20. (d) p
Q nC T
= D and W PΔV nRΔT.
= =
For monatomic gas,
2
R
5
Cp = .
W 2
Q 5
Þ =
21. (c)
1
2
1
2
1
2
1
2
T
T
Q
Q
T
T
1
Q
Q
1 =
Þ
-
=
-
=
h
So K
250
300
500
150
Q
T
Q
T
1
1
2
2 =
´
=
´
=
22. (d) Efficiency,
T2
= 1 –
T
1
η
T1 (source temp.) = 400 K
T2 (sink temp.) = 300 K
300 1
25%
400 4
= 1 – = =
h
23. (c)
)
1
4
.
1
(
2
)
1
4
.
1
(
4
V
.
T
V
)
300
(
-
-
÷
ø
ö
ç
è
æ
=
4
.
0
2 )
4
(
)
300
(
T =
24. (d) From C to D, V is constant. So process is isochoric.
From D to A, the curve represents constant
temperature. So the process is isothermal.
From A to B, pressure is constant . So, the process is
isobaric.
BC represents constant entropy.
25. (d) In cylinder A, heat is supplied at constant pressure
while in cylinder Bheat issupplied at constant volume.
(DQ)A =nCP(DT)A
and (DQ)B = nCV (DT)B
Given : (DQ)A =(DQ)B
(DT)B
P
A
V
C
( T)
C
1.4 30
42K
= D
= ´
=
[Q for diatomic gas P
V
C
1.4
C
= ]
26. (b)
2
1
T
1
T
273 0
1
273 200
200
473
h = -
+
= -
+
=
2
1
T
' 1
T
(273 200)
1
273 0
200
473
h = -
-
= -
+
=
200 273
' 473 200
0.577
h
= ´
h
=
27. (a)
250
300
250
W
750
-
=
Heat rejected = 750 + 150 = 900 cal.
28. (b)
1
2
1
T
T
T -
is maximum in case(b).
29. (c) For adiabatic process, dU = – 100 J
which remains same for other processes also.
Let C be the heat capacity of 2nd process then
–(C) 5 = dU + dW
= – 100+ 25 = – 75
C = 15J/K
30. (c) According to first law of thermodynamics
Q = DU + W
DU = Q – W
= 2 × 4.2 × 1000 – 500
= 8400 –500 = 7900 J
31. (a) PV3/2 = K](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-325-320.jpg)

![323
Thermodynamics
43. (a) Initial and final condition is same for all process
DU1 = DU2 = DU3
from first law of thermodynamics
DQ= DU + DW
Work done
DW1 > DW2 > DW3 (Area of P.V. graph)
So DQ1 > DQ2 > DQ3
44. (d) Efficiency
1
W
h =
q
and W = q1 – q2
1 2
1
–
q q
h =
q
= 2
1
1
q
-
q
45. (b) P1 > P2
P1
P2
T
V
q2
q1
As V = constant Þ Pµ T
Hence from V–T graph P1 > P2
46. (b) Change in internal energy do not depend upon the
path followed by the process. It onlydepends on initial
and final states i.e.,
DU1 = DU2
47. (a) For adiabatic process Q = 0.
Byfirst law of thermodynamics,
Q = DE + W
Þ DEint = – W.
48. (d) The efficiency of carnot's heat engine
2
1
T
1–
T
h =
where T2 is temperature ofsink, and T1 is temperature
of hot reservoir or source.
When efficiencyis 40% i.e. h = 40/100 =
2
1
T
1–
T
or
2
1
T
2
1– [T T(given)]
5 T
= =
T2=
3
T
5
Now, when efficiency is 50%
1
1
3
T
50 6
5
1– T T
100 5
T
h = = =
49. (a) 50. (c)
EXERCISE - 3
Exemplar Questions
1. (c) For the straight line in the graph denoted by 4, that
shows pressure is constant, so curve 4 represents an
isobaric process.
p
V
1
2
3
4
For the straight line in graph denoted by1, that shows
volume is constant, so curve 1 represents isochoric
process. Out of curves 3 and 2, curve 2 is steeper.
Hence, curve 2 is adiabatic and curve 3 is isothermal.
2. (a) As we know that amount of sweat evaporated/minute
Sweat produced/ minute
Number of calories required for evaporation/kg
=
Amount of heat produced per minute in jogging
Latent heat (in cal/kg)
=
580 × 103 calories are needed to convert
1 kg H2O into stream.
1 cal. will produce sweat = 1 kg/ 580 × 103
14.5 × 103 cal will produce (sweat)
3
3
14.5 10 145
kg= kg/m
580
580 10
´
=
´
=0.025kg.
3. (c) According to given P–V diagram that
pV = constant
So we can say that the gas is going through an
isothermal process.
Ifpressure (P)increase at constant temperature volume
V decreases, the graph (iii) shows that pressure (P) is
smaller at point 2 and larger at point 1 point sothe gas
expands and pressure decreases. Hence verifiesoption
(c).
4. (b) According to the given p-V diagram.
Work done in the process ABCD
= (AB) × BC = (3V0 – V0) × (2p0 – p0)
= 2V0 × p0 = 2p0V0
Here the direction of arrow is anti-clockwise, sowork
done is negative.
Hence, work done by the gas = –2p0V0
That shows external work done on the system.
5. (a) Let us consider the p-V diagram for container A
(isothermal) and for container B (adiabatic).](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-327-320.jpg)
![324 PHYSICS
2 2
1 1
p p
p0 p0
V0 V0
2V0 2V0
V V
Container
(Isothermal)
A Container
(Adiabatic)
B
In both process compression of the gas.
For isothermal process (gas A) during 1®2
1 1 2 2
p V p V
= 1 0 2 0
( 2 , )
V V V V
= =
Q
0 0 2 0
(2 ) ( )
p V p V
=
2 0
2
p p
=
For adiabatic process, (gas B)during (1®2)
1 2
1 2
p V p V
g g
= 1 0 2 0
( 2 , )
V V V V
= =
Q
0 0 2 0
(2 ) ( )
p V p V
g g
=
0
2 0 0
0
2
(2)
V
p p p
V
g
g
æ ö
= =
ç ÷
è ø
So, ratio of final pressure
1
0
2
1 0
(2)
( )
2
( ) 2
A
p
p
p p
g
g -
B
æ ö
= = =
ç ÷
è ø
where, g is ratio of specific heat capacities for the gas.
Hence, verifies the option (a).
6. (b) Consider the equilibrium temperature ofthe system is
T.
Let us consider, T1, T2 < T < T3.
As given that, there is no net loss to the surroundings.
Heat lost by M3 = Heat gained by M1
+ Heat gained by M2
3 3 1 1 2 2
( ) ( ) ( )
M s T T M s T T M s T T
- = - + -
3 3 3 1 1 1
M sT M sT M sT M sT
- = -
2 2 2
M sT M sT
+ -
(where, s is specified heat ofthe copper material)
1 2 3 3 3 1 1 2 2
[ ]
T M M M M T M T M T
+ + = + +
1 1 2 2 3 3
1 2 3
M T M T M T
T
M M M
+ +
=
+ +
NEET/AIPMT (2013-2017) Questions
7. (a) Wnet = Area of triangleABC
=
1
2
AC × BC
=
1
2
× 5 × 10–3 × 4 × 105 = 1000 J
8. (c) According to question P µ T3
But as we know for an adiabatic process the
pressure P µ 1
T
g
g -
.
So,
1
g
g -
= 3 Þ g =
3
2
or,
,
p
v
C
C
=
3
2
9. (a) From first law ofthermodynamics
Qadc = DUadc + Wadc
50J = DUadc + 20 J
DUadc = 30J
Again, Qabc = DUabc + Wabc
Wabc = Qabc – DUabc
= Qabc – DUadc
= 36 J – 30 J
= 6 J
10. (a) Adiabatic equations of state are
PVg = constant
TVg–1 = constant
P1–gTg = constant.
11. (d) Efficiency of engine A, 1
1
1 ,
T
T
h = -
Efficiencyof engine B, 2
2 1
T
T
h = -
Here, h1 = h2
2
1
T
T
T T
= Þ 1 2
T T T
=
12. (d) Work done by the system in the cycle
=Area under P-V curve andV-axis
= 0 0 0 0
1
(2P P )(2V V )
2
- - +
0 0 0 0
1
(3P 2P )(2V V )
2
é ù
æ ö
- - -
ç ÷
ê ú
è ø
ë û
=
0 0 0 0
P V P V
0
2 2
- =
13. (c) For isothermal process P1V1 = P2V2
Þ PV= P2(2V) Þ P2 =
P
2
For adiabatic process
2 3
2 3
P V P V
g g
=
Þ 3
P
(2v) P 16v)
2
g g
æ ö
=
ç ÷
è ø
Þ P3 =
5/3
3 1 P
2 8 64
æ ö
=
ç ÷
è ø](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-328-320.jpg)













![338 PHYSICS
NEET/AIPMT (2013-2017) Questions
9. In the given (V – T) diagram, what is the relation between
pressure P1 and P2 ? [2013]
(a) P2 > P1
(b) P2 < P1
T
V
P2
P1
q1
q2
(c) Cannot be predicted
(d) P2 = P1
10. The amount of heat energyrequired to raisethe temperature
of 1g ofHelium at NTP, from T1K toT2K is [2013]
(a)
3
2
NakB(T2 – T1)
(b)
3
4
NakB(T2 – T1)
(c)
3
4
NakB
2
1
T
T
(d)
3
8
NakB(T2 – T1)
11. In a vessel, the gas is at a pressure P. If the mass of all the
molecules is halved and their speed is doubled, then the
resultant pressure will be [NEET Kar. 2013]
(a) 4P (b) 2P
(c) P (d) P/2
12. The mean free path of molecules of a gas, (radius ‘r’) is
inversely proportional to : [2014]
(a) r3 (b) r2
(c) r (d) r
13. The ratio of the specific heats
p
v
C
C
= g in terms of degrees
of freedom (n) is given by [2015]
(a)
n
1
3
æ ö
+
ç ÷
è ø
(b)
2
1
n
æ ö
+
ç ÷
è ø
(c)
n
1
2
æ ö
+
ç ÷
è ø
(d)
1
1
n
æ ö
+
ç ÷
è ø
14. One mole of an ideal diatomic gas undergoes a transition
from Ato B along a path AB as shown in the figure.
P(in kPa)
V(in m )
3
2
5
A
B
4 6
The change in internal energy of the gas during the
transition is: [2015]
(a) – 20 kJ (b) 20J
(c) –12kJ (d) 20kJ
15. Two vessels separately contain two ideal gases A and B at
the same temperature. The pressure ofAbeing twice that of
B. Under such conditions, the density of A is found to be
1.5 times the densityofB. The ratio of molecular weight of
A and B is : [2015 RS]
(a)
3
4
(b) 2
(c)
1
2
(d)
2
3
16. 4.0 g of a gas occupies 22.4 litres at NTP. The specific heat
capacity of the gas at constant volume is 5.0JK–1. If the
speed of sound in this gas at NTP is 952 ms–1, then the
heat capacity at constant pressure is (Take gas constant R
= 8.3 JK–1 mol–1) [2015 RS]
(a) 7.5 JK–1 mol–1
(b) 7.0 JK–1 mol–1
(c) 8.5 JK–1 mol–1
(d) 8.0 JK–1 mol–1
17. The molecules of a given mass of a gas have r.m.s. velocity
of 200 ms–1 at 27°C and 1.0 × 105 Nm–2 pressure. When the
temperature and pressure ofthe gas are respectively, 127°C
and 0.05 × 105 Nm–2, the r.m.s. velocity ofits molecules in
ms–1 is : [2016]
(a) 100 2 (b)
400
3
(c)
100 2
3
(d)
100
3
18. Agas mixture consists of 2 moles ofO2 and 4 moles ofAr at
temperature T. Neglecting all vibrational modes, the total
internal energy of the system is :- [2017]
(a) 15RT (b) 9 RT
(c) 11 RT (d) 4 RT](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-342-320.jpg)


![341
Kinetic Theory
20. (c) According to Dalton’s Law
P= P1 +P2.....................
here 1 litre of orygen at a pressure of1atm, & 2 litre of
nitrogen at a pressure of 5 atm are introduced in a
vessel of 1 litre capacity.
so 1 1 2 2
V P P V 1 1 2 .5
P 2atm
volumeof vessel 1
+ ´ + ´
= = =
21. (b) Relative humidity %
100
M
m
´
=
where m is the mass of vapour actually present in
certain volume of air & M is the mass required to
saturate the air fully of that volume
so %
75
100
20
15
H
.
R =
´
=
22. (c) Bydefinition
Þ
100
60
;
100
.
temp
room
at
P
.
V
.
S
.
temp
room
at
P
.
V
H
.
R ´
=
15
(V.P.)
12.67
=
(V.P)15 = 7.6mm of Hg.
Now since unsaturated vapour obeys gas equation &
mass of water remains constant so
nRT
P PαT
V
æ ö
= Þ
ç ÷
è ø
15
20
20
(V.P) 273 15
(V.P)
(V.P) 273 20
+
= Þ
+
=7.73 mm ofHg
So
20
20
20
(V.P)
(R.H) 100 44.5%
(S.V.P)
= ´ =
23. (a)
273
327
273
t
)
v
(
)
v
(
1
rms
2
rms
+
+
= or
1 273
2 600
t +
=
or t = – 123ºC
24. (a)
1
1
1
T
V
P
= constant for one mole
&
1
1
T
P
= constant for constant volume
so 1 1
1
1 1
P 1.004P
T 250K
T (T 1)
= Þ =
+
25. (d) Total K.E. ofAtype molecules 2
m
2
3
w
=
Total K.E. ofAtype of molecule is
[ ]
2
z
ms
.
r
2
y
ms
.
r
2
x
ms
.
r
A )
v
(
)
v
(
)
v
(
m
2
1
E
.
K +
+
=
but w
=
x
ms
.
r )
v
(
so w
=
= z
ms
.
r
y
ms
.
r )
v
(
)
v
(
Total K.E. of B type molecules
2 2
1
2 m v m v
2
= ´ =
Now, 2 2
3
m ω m v
2
´ = or
2 2 2
( ω / v )
3
=
26. (d) rms
v T
µ
At 0ºC, rms
v 273
µ
At temp. T, rms
v
T
2
µ
K
69
~
K
2
.
68
4
273
T
or
273
T
2
1
-
=
=
=
C
º
204
273
69
T -
=
-
=
27. (c) For a monatomic gas
R
2
3
Cv =
So correct graph is
v
C
R
2
/
3
®
T
28. (d) Molar volume = 22400 cm3
Bubble volume =
3
3
4 d 4
10
3 8 3
-
p = p
No. of molecules
23 3
17
6 10 4 10
10
22400 3
-
´ ´ p
= »
´
29. (d) Molecule number ratio is
3
1
:
3
2
O
:
H 2
2 = .
That gives
2 1
2
(c ) 16 1
rms
3 3
= +
æ ö æ ö
è ø è ø
times the
value for O2.
30. (b) The Vander waal’s equation of state is
RT
)
b
V
(
V
a
P
2
=
-
÷
÷
ø
ö
ç
ç
è
æ
+ or 2
V
a
b
V
RT
P -
-
=
At the critical point, P = Pc, V = Vc, and T = Tc
2
c
c
c
c
V
a
b
V
RT
P -
-
= ....(i)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-345-320.jpg)
![342 PHYSICS
At the critical point on the isothermal, 0
dV
dP
c
c
=
c
2 3
c c
RT 2a
0
(V b) V
-
= +
-
or 3
c
2
c
c
V
a
2
)
b
V
(
RT
=
-
....(ii)
Also at critical point, 0
dV
P
d
2
c
c
2
=
4
c
3
c
c
V
a
6
)
b
V
(
RT
2
0 -
-
= or
c
3 4
c c
2RT 6a
(V b) V
=
-
..(iii)
Dividing (ii) by (iii), weget
c
c V
3
1
)
b
V
(
2
1
=
- or Vc = 3 b ....(iv)
Putting this value in (ii), we get
2 3
RTc 2a
4b 27 b
= or
R
b
27
a
8
Tc = ...(v)
Putting the values of Vc and Tc in (i), we get
2
2
c
b
27
a
b
9
a
R
b
27
a
8
b
2
R
P =
-
÷
÷
ø
ö
ç
ç
è
æ
=
31. (c) g for resulting mixture should be in between 7/5 and
5/3.
32 (b) For 1 molecule of a gas, vrms =
3KT
m
where m is the mass of one molecule
For N molecule of a gas, v1= 3KT N
m
´
For 2N molecule of a gas v2 =
3KI N
N
(2m)
´
´
1
2
v
1
v
=
33. (a) Since VP2 = constant,
2 '2
VP 2VP
=
P
P'
2
=
As
P
constant or Tα P,
T
= thusT becomes T/Ö2
34. (a) We know that, ÷
ø
ö
ç
è
æ g
=
M
RT
Crms
Here 1
2
rms 2
rms
rms 1
C m
1
C ;
M C m
æ ö
µ = ç ÷
è ø
35. (b) 3 12 2 13
dU d M N 6M 12N
F
dr dr r R r r
-
é ù é ù
= = - - = - +
ê ú ê ú
ë û ë û
In equilibrium position, F = 0
2 13
6M 12N
0
r r
- = or,
6 2N
r
M
=
Potential energyat equilibrium position
2 2 2
2
M N M M M
U
(2N / M) 2N 4N 4N
(2N / M)
= = = - =
36. (b) 1 1 2 2
1 2
P V P V
T T
= Here, P1 =200kPa
T1 =22°C =295K T2 =42°C =315K
V2 1 1 1
2
V V 1.02V
100
= + =
1
2
1
200 315V
P
295 1.02V
´
=
´
209.37kPa
=
37. (a) According to given Vander Waal's equation
2
2
nRT n
P
V n V
a
= -
- b
Workdone,
2 2 2
1 1 1
2
2
V V V
V V V
dV dV
W PdV nRT n
V n V
= = - a
- b
ò ò ò
[ ]
2
2
1
1
2 1
log ( )
V
V
e V
V
nRT V n n
V
é ù
= - b + a ê ú
ë û
2
2 1 2
1 1 2
loge
V n V V
nRT n
V n V V
æ ö é ù
- b -
= + a
ç ÷ ê ú
- b
è ø ë û
38. (d) Internal energyof 2 moles of oxygen
2
5 5
Uo µ RT 2. RT 5RT
2 2
æ ö
= = =
ç ÷
è ø
Internal energyof 4 moles ofArgon.
Ar
3 3
U µ RT 4. RT 6RT
2 2
æ ö
= = =
ç ÷
è ø
Total internal energy
2
O Ar
U U U 11RT
= + =
39. (c)
1 v 2 v
1 2
vmix
1 2
n C n C
C
n n
+
=
+
Þ
1 v 1 v
1 2
1 1
n C 2n C
13R
6 n 2n
+
=
+
1
2
n 1
n 2
é ù
=
ê ú
ë û
Q
Þ v v
1 2
13R
C 2C
2
= +](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-346-320.jpg)

![344 PHYSICS
EXERCISE - 3
Exemplar Questions
1. (b) As the relative velocity of molecule with respect to
the walls of container does not change in rocket, due
to the mass ofa molecule is negligible with respect to
the mass of whole system and system of gas moves
as a whole and (g = 0) on molecule energy where.
Hence pressure of the gas inside the vessel, as
observed by us, on the ground remain the same.
2. (d) Pressure on the wall due to force exerted bymolecule
on walls due to its rate of transfer of momentum to
wall.
In an ideal gas, when a molecule collides elastically
with a wall, themomentum transferredto each molecule
will betwice themagnitude ofits normal momentum is
2 mv. For the wall EFGH, absorbs those molecules.
Which strike toit so rate of change in momentum toit
become only mv so the pressure of EFGH would half
ofABCD.
3. (b) Boyle's law is applicable at constant temperature and
temperature remains constant in isothermal process.
For ideal gas, pV = nRT = constant
So, pV = constant (at constant temperature)
1
p
V
µ
So, this process can be called as isothermal process.
4. (c) Let us consider the given diagram where an ideal gas
is contained in a cylinder, having a piston of mass M.
The pressure on gas does not change.
M
p
pa
p
pa Mg/A
A
The pressure inside the gas will be
p = pa + Mg /A
where, pa = atmospheric pressure
A = area of cross-section of the piston.
Mg = weight of piston
Hence, p = constant.
As the piston and cylinder is frictionless so the
equation for ideal gas
pV = nRT, volume (V) increases at constant pressure.
as p, R, n are constant so,
V T
µ
so on increasing temperature of system its volume
increased but pwill remain constant.
5. (a) As we know that an ideal gas equation,
as the pressure and quantity of gas in system are
constant
nR
pV nRT V T
p
æ ö
= Þ = ç ÷
è ø
T
V
p
µ as n, R are constant
1
V
T p
æ ö
µ ç ÷
è ø
Slope of the V – T graph,
dV nR
m
dT p
= = [m = slope of V – t graph]
1
dV
dT p
µ or
1
m
p
µ [Q nR = constant]
So,
1
p
m
µ
hence, 1 2
2 1
=
p m
p m
where, m1 is slope of the graph corresponding to p1
and similarlym2 is slope corresponding to p2. Soslope
of p1
is smaller than p2
. Hence, (p1
> p2
).
6. (d) Pressure exerted by gas is due to rate of change of
momentum (p) imparted byparticles to wall.
When the molecules breaks into atoms, the number of
moles would become twice.
From ideal gas equation,
pV = nRT
where, p = Pressure of gas, n = Number of moles
R = Gas constant, T = temperature
As gases breaks number of moles becomes twice of
initial, so n2 = 2n1
So, p nT
µ
or
2 2 2 1
1 1 1 1
(2 )(3000)
20
(300)
p n T n
p n T n
= = =
So, p2 = 20p1
Hence, final pressure of the gas would be 20 times to
the initial pressure.
7. (b) For a function f1(v) thenumber ofmolecules (n) which
will have their speeds between v and v + dv.
For each function f1(v) and f2(v) number of molecules
remain same 1 mole each but due to mass difference
their speed will be different.
Hence both gases of each function f1(v) and f2(v) will
obeythe Maxwell's distribution law separately.
8. (d) As we know that an ideal gas equation,
pV = nRT
where, n = Number of moles, p = Pressure,
V = Volume, R = Gas constant,
T = Temperature
pV
n
RT
=
If n, R are constant for the system or as number of
moles of the gas remains fixed, hence, we can write
pV
T
= constant
or
1 1 2 2
1 2
p V p V
RT RT
=](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-348-320.jpg)
![345
Kinetic Theory
2
2 1 1
2 1
( )
T
p p V
V T
æ ö
= ç ÷
è ø
( )( )(1.1 )
(1.05) ( )
p V T
V T
= [p1 = p, V2 = 1.05 V
and T2 = 1.1 T]
1.1
1.05
p
æ ö
= ´ç ÷
è ø
= p(1.0476)
So, final pressure p2
will lies between p and 1.1p.
NEET/AIPMT (2013-2017) Questions
9. (b) P1 > P2
P1
P2
T
V
q2
q1
As V = constant Þ Pµ T
Hence from V–T graph P1 > P2
10. (d) From first law ofthermodynamics
DQ = DU+ DW =
3
2
.
1
4
R (T2 – T1) + 0
=
3
8
NaKB (T2 – T1) [Q K =
R
N
]
11. (b) Q 2
rms
1
3
mn
P V
V
=
When mass is halved and speed is doubled then
Resultant pressure, Pt =
2
rms
1
(2 )
3 2
m n
v
V
´ ´
= 2 P.
12. (b) Mean free path lm = 2
1
2 d n
p
where d = diameter of molecule and d = 2r
lm µ 2
1
r
13. (b) Let ‘n’ be the degree of freedom
p
v
n
1 R
C 2
2
1
n
C n
R
2
æ ö
+
ç ÷
è ø æ ö
g = = = +
ç ÷
è ø
æ ö
ç ÷
è ø
14. (a) Change in internal energyfrom A® B
DU=
f
2
nRDT =
f
2
nR (Tf – Ti)
=
5
2
{PfVf –PiVi}
(As gas is diatomic f = 5)
=
5
2
{2 × 103 × 6 – 5 × 103 × 4}
=
5
2
{12 – 20} × 103 J= 5 × (–4) × 103 J
DU= –20 KJ
15. (a) FromPV=nRT
PA = A A
M
RT
r
and B B
B
M
P
RT
r
=
From question,
A A A A
B B B B
P M M 3
2
P M M 2
r
= = =
r
So,
A
B
M 3
M 4
=
16. (d) Molar mass of the gas = 4g/mol
Speed of sound
V =
RT
m
g
Þ 952= 3
3.3 273
4 10-
g´ ´
´
Þ g = 1.6 =
6 8
10 5
1
=
Also, g =
P
V
C 8
C 5
=
So, CP =
8 5
5
´
= 8JK–1mol–1 [CV = 5.0 JK–1 given]
17. (b) Here v1 = 200 m/s;
temperature T1 = 27°C = 27 + 273 = 300 k
temperature T2 =127°C=127+273=400 k,V=?
R.M.S. Velocity, Vµ T
Þ
v 400
200 300
=
Þ v =
200 2
m / s
3
´
Þ v =
400
m / s
3
18. (c) Internal energy of the system is given by
U=
f
nRT
2
Degree of freedom
Fdiatomic = 5
fmonoatomic = 3
and, number of moles
n(O2)= 2
n(Ar) = 4
Utotal =
5 3
(2)RT (4)RT
2 2
+ = 11RT
T](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-349-320.jpg)

![348 PHYSICS
SOME SYSTEMS EXECUTING S.H.M.
Case 1 Spring mass system :
(i) When two springs having force constants k1 and k2
connected in parallel, then
k2
k1
M
The force constant of the combination is
k = k1 + k2 and hence T = 2p[M/(k1 + k2)]1/2
(ii) When two springs of force constants k1 and k2 are
connected in series, then
k2
k1
M
The force constant of the combination is
1/k = 1/k1 + 1/k2. i.e.,
k = k1k2/(k1 + k2) Hence 2
m
T
K
= p
(iii) If two mass M1 and M2 are connected at the two ends of
the spring, then their period of oscillation is given by
M2
M1
T = 2p[m/k)]1/2 where 1 2
1 2
M M
M M
m =
+
is the reduced mass.
(iv) When the length of spring increases, spring constant
decreases. If thelength ofspring becomes n times, its spring
constant becomes
n
1
times and therefore time period will
be increased by n times.
(v) If we divide the spring into n equal parts, the spring
constant of each part becomes n k. Hence time period when
the same mass is suspended from each part is:
1/2
2
M
T
nk
é ù
= pê ú
ë û
Case 2 Simple pendulum : A simple pendulum consists of a
point mass suspended by a weightless inextensible cord from a
rigid support.
q
x =lq
mg sinq mg mg cosq
l l
Let a bob of mass m is displaced from its, equilibrium position
and released, then it oscillates in a vertical plane under gravity.
Let q be the angular displacement at any time t, then
corresponding linear displacement along the arc is
x = lq.
It is clear from the diagram that mg sinq, is the restoring force
acting on m tending to return it to mean position. So from
Newton’s second law
q
-
=
= sin
mg
dt
x
md
F
2
2
...(i)
where negative sign indicates that restoring force mg sin q (= F)
is opposite to displacement q. If q is very small, then
sin q » q, so from equation (i)
l
x
mg
sin
mg
dt
x
md
2
2
-
=
q
-
= or ...(ii)
where w2 = g/l.
This is the equation of S.H.M. of the bob with time period
2
2
T
g
æ ö
p
= = p ç ÷
w è ø
l
OM
How to find the time period of a body undergoing S.H.M.?
Step 1 : First, find the equilibrium position. Equilibrium position
will be one for which 0
F =
S and 0
St =
Step 2 :Displacethebody, from the equilibrium position byx.
Find therestoring force acting on the bodyF = –kx (for translation)
Find the restoring torque acting on the body q
-
=
t k (for
rotational)
Step 3 : Since 2
2
dt
x
md
ma
F =
=
Use kx
dt
x
md
2
2
-
= ... (i) for translational
q
-
= k
dt
x
md
2
2
… (ii) for rotational
Step 4 :
k
m
2
T p
= (for translational)
k
I
2
T p
= (for rotational) where, I = moment ofinertia
COMMON DEFAULT
Incorrect. The time period of spring mass-system is
dependent on the value of g.
Correct. Time period ofspring-mass system shifts onlythe
equilibrium position. It does not change the time period.
Because of this reason, time period of spring mass system
remains same on plains / mountains / in satellites.
Incorrect. The time taken tocover halfthe amplitude form
equilibrium position is
8
T
.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-352-320.jpg)
![349
Oscillations
Correct. The actual time taken is
12
T
.
Incorrect. In a spring mass system, mass oscillate about
the end of a spring when the spring is in unstretched
condition.
Correct. Themass oscillates about the equilibrium position
which may or may not be at the unstretched length.
Case 3 Liquid in U-tube :AU-tube ofuniform cross-sectional
area A has been set up vertically with open ends facing up.
x
x
[Restoring force = –2Adg x]
If m gm of a liquid of densityd is poured into it then time period
of oscillation.
Adg
2
m
2
T p
=
Case 4 Rectangular block in liquid :
d
h'
h
d'
Rectangular block floating in a liquid,
gd
'
d
'
h
2
T p
= ; where
d = density of liquid, d¢ = density of block, h = height of block
Case 5 : Vibration of gas system in a cylinder with frictionless
piston.
A
m
p
h
Time period,
AP
mh
2
T p
=
where m = mass of gas, A = cross sectional area of piston
P = pressure exerted by gas on the piston, h = height of piston
Case 6: If a tunnel is dig in the earth diametrically or along a
chordthen timeperiod, sec
36
min
84
g
R
2
T =
p
= for a particle
released in the tunnel.
Case 7: The time period of a ball oscillating in the neck of a
chamber
B
mV
A
2
T
p
=
Case 8 : Ifa dipole of dipole moment p is suspended in a uniform
electric field E then time period of oscillation
PE
I
T p
2
=
Keep in Memory
1. In S.H.M. the phase relationship between displacement,
velocity and accleration, is as follows :
(a) The velocity is leading the displacement by a phase
2
p
radian
(b) The acceleration is leading the displacement by a
phase p radian
(c) The acceleration is leading the velocity bya phase
2
p
radian.
2. (a) When
2
A
x = , then velocityV = 0.86Vmax.
(b) When V = Vmax/2, the displacement x = 0.87A.
(c) When
2
A
x = , the kineticenergyof S.H.M. is 75% of
the total energy and potential energy25% of the total
energy.
(d) When the kinetic energyof S.H.M. is 50% of the total
energy, the displacement is 71% of the amplitude.
3. The time period of a simple pendulum of length l which is
comparable with radius of earth.
1/2
1/2
R R
T 2 2
R ( R)g
1 g
é ù
é ù
= p = p ê ú
ê ú +
æ ö ë û
ê ú
+
ç ÷
è ø
ê ú
ë û
l
l
l
where R = radius of the earth and g is the acceleration due
to gravity on the surface of the earth.
(a) When l << R, then
g
2
T
l
p
=
(b) When l = R, we find hour
1
g
2
R
2
T
2
/
1
»
ú
ú
û
ù
ê
ê
ë
é
p
=
(c) When l = ¥ , then
2
/
1
g
R
2
T
ú
ú
û
ù
ê
ê
ë
é
p
= = 84.6 minutes. Thus maximum ofT
is 84.6 minutes.
(d) Under weightlessness or in the freely falling lift
¥
=
ú
û
ù
ê
ë
é
p
=
2
/
1
0
2
T
l
. This means, the pendulum does
not oscillate at all.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-353-320.jpg)



![353
Oscillations
1
2
1
2
1 k
1
k
2
1
k
or
k
1
k
2
1
k
1
-
ú
û
ù
ê
ë
é
+
=
ú
û
ù
ê
ë
é
+
=
Example3.
A particle starts with S.H.M. from the mean position as
shown in figure below. Its amplitude isA and its time period
is T. At one time, its speed is half that of the maximum
speed. What is this displacement at that time ?
(a)
2 A
3
(b)
3 A
2
(c)
2A
3
(d)
3A
2
Solution : (b)
We know that 2 2 1/ 2
v ω[A x ]
= -
1/ 2
2
2
2
v
x A
ω
é ù
= -
ê ú
ê ú
ë û
Given that
max
v Aω
v
2 2
= = .
so, A
.
2
3
4
A
A
2
/
1
2
2
2
2
=
ú
ú
û
ù
ê
ê
ë
é
w
w
-
Example4.
A cylindrical piston of mass M slides smoothly inside a
long cylinder closed at one end, enclosing a certain mass
of gas. The cylinder is kept with its axis horizontal. If the
piston is disturbed from its equilibrium position, it
oscillates simple harmonically. The period of oscillation
will be
P A
M
h
(a)
Mh
T 2π
PA
æ ö
= ç ÷
è ø
(b)
MA
T 2π
Ph
æ ö
= ç ÷
è ø
(c)
M
T 2π
PAh
æ ö
= ç ÷
è ø
(d) T 2π (MPhA)
=
Solution : (a)
We know that PV = R T
)
V
/
V
(
P
P
or
0
V
P
P
V D
=
D
=
D
+
D
or ÷
ø
ö
ç
è
æ
-
=
÷
÷
ø
ö
ç
ç
è
æ
-
=
h
x
P
h
A
x
A
P
A
F
÷
ø
ö
ç
è
æ
-
=
h
x
A
P
F x
h
M
A
P
M
1
h
x
A
P
a ÷
÷
ø
ö
ç
ç
è
æ
-
=
÷
ø
ö
ç
è
æ
-
=
This gives, 2 2
2
æ ö
= = = ç ÷
è ø
P A M h
or T
M h P A
p
w p
w
Example5.
A simple harmonic oscillator has an amplitude A and time
period T. Determine the time required by it to travel from
x = A to
2
A
x = .
Solution :
For S.H.M., ÷
ø
ö
ç
è
æ p
= t
T
2
sin
A
x
When x =A, ÷
ø
ö
ç
è
æ p
= t
.
T
2
sin
A
A
1
t
.
T
2
sin =
÷
ø
ö
ç
è
æ p
Þ ÷
ø
ö
ç
è
æ p
=
÷
ø
ö
ç
è
æ p
2
sin
t
.
T
2
sin Þ t = (T/4)
When
2
A
x = and ÷
ø
ö
ç
è
æ p
= t
.
T
2
sin
A
2
A
or ÷
ø
ö
ç
è
æ p
=
p
t
T
2
sin
6
sin or t = (T/12)
Now, time taken to travel from
x =A to x =A/2 = T/4 –T/12 = T/6
Example6.
Calculate the increase in velocity of sound for 1ºC rise of
temperature, if the velocity of sound at 0ºC is 332 m/sec.
Solution :
t
1
0 0
1/2
1 0 0
0 0 0
t 0 0
T
v 273 t
;
v T 273
t t
v v 1 v 1
273 2 273
t t
v 1 v v
546 546
t
v v v = 0.61 m/sec.
546
æ ö +
æ ö
= = ç ÷
ç ÷ è ø
è ø
æ ö æ ö
= + = +
ç ÷ ç ÷
è ø è ø
´
æ ö æ ö
= + = +
ç ÷ ç ÷
è ø è ø
æ ö
- = ç ÷
è ø
(As v0 = 332 m/sec and Dt = 1ºC)
Example7.
Which one of the following equations does not represent
S.H.M.; where x = displacement and t = time. Parameters
a, b and c are the constants of motion
(a) x = a sin bt
(b) x = a cos bt + c
(c) x = a sin bt + c cos bt
(d) x = a sec bt + c cosec bt
Solution : (d)
Sec bt is not defined for bt = p/2.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-357-320.jpg)
![354 PHYSICS
x = a sec bt + c cosec bt =
bt
cos
bt
sin
bt
cos
c
bt
sin
a +
This equation cannot be modified in the form of simple
equation of S.H.M.
i.e. x = a sin (wt + f).
so, it cannot represent S.H.M.
Example8.
If length of pendulum is increased, time period T increases.
So, frequency decreases or angular velocity decreases. As
maximum velocity max
v Aω
= , so max. velocity will also
decrease. (where A is amplitude of bob).
A pendulum bob has a speed of 3 m/s at its lowest position.
The pendulum is 0.5 m long. What will be the speed of the
bob, when the length makes an angle of 60º to the vertical?
(g = 10 m/s2)
Solution :
Here, r w = 3 m/s; l = 0.5 m; K.E. at the lowest point
m
2
9
)
3
(
m
2
1
r
m
2
1 2
2
2
=
=
w
=
Letv bethevelocityofthe bobatB when ÐOAB= 60° then,
A
O
C B
60º
l
OC = h = (l – l cos q) = (l – l cos 60º) = l /2
If v is the velocity of bob at position B, then using law of
conservation of energy, we have,
2
1 1
m 9 m v mg (1 cos θ)
2 2
´ = + -
l
or
2
1 1
m v m 9 mg (1 cos θ)
2 2
= ´ - -
l
1/2
1/2
1/2
[9 2 (1 cos )]
[9 2 10 0.5 (1 1/ 2)]
(9 – 5) 2 /
= - -
= - ´ ´ -
= =
l
v g
m s
q
Example9.
A small spherical steel ball is placed a little away from the
centre of a large concave mirror whose radius of curvature
R = 2.5 cm. When the ball is released, it begins to oscillate
about the centre. Show that the motion of the ball is simple
harmonic and find the period of motion. Neglect friction
and take g = 10 m/sec2.
Solution :
F = – mg sin q = – mg q (Q q issmall)
= – mg (x/R)
F= – kx, wherek = (mg/R)
Now, a = F/m = – kx/m = – w 2x
Hence, motion is simpleharmonic motion and
T =
2p
w
=
R
2
g
æ ö
p ç ÷
è ø
= 2 × 3.14 ×
2.5
10
æ ö
ç ÷
è ø = 3.142 sec.
Example10.
A spring of stiffness constant k and natural lengthl is cut
into two parts of length 3l / 4 and l / 4 respectively, and an
arrangement is made as shown in the figure. If the mass is
slightly displaced, find the time period of oscillation.
m
(3/4)l l/4
Solution :
The stiffness of a spring is inversely proportional to its
length. Therefore the stiffness of each part is
1
4
k k
3
= and k2 = 4k
m
k k
1 = (4/3) k k
2 = 4
Timeperiod,
1 2
m
T 2
k k
= p
+
or
3m 3m
T 2
16k 2 k
p
= p =](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-358-320.jpg)



![359
Oscillations
19. A boy is executing simple Harmonic Motion. At a
displacement x its potential energy is E1 and at a
displacement y its potential energy is E2. The potential
energyE at displacement (x + y) is
(a) 1 2
E E E
= - (b) 1 2
E E E
= +
(c) 1 2
E E E
= + (d) 1 2
E E E
= -
20. A particle undergoes simpleharmonic motion having time
period T. The time taken in 3/8th oscillation is
(a) T
8
3
(b) T
8
5
(c) T
12
5
(d) T
12
7
21. Twoparticles are executing S.H.M. of same amplitude and
frequency along the same straight line path. They pass
each other when going in opposite directions, each time
their displacement is half of their amplitude. What is the
phase difference between them ?
(a) 5p/6 (b) 2p/3
(c) p/3 (d) p/6
22. Lissajous figure obtained by combining x = a sin wt and
y= a sin (wt + p/4) will be a/an
(a) ellipse (b) straight line
(c) circle (d) parabola
23. A simple spring has length l and force constant K. It is cut
into two springs of lengths l1 and l2 such that l1 = n l2
(n = an integer). The force constant ofspring of length l1 is
(a) K(1 + n) (b) (K/n)(1 + n)
(c) K (d) K/(n + 1)
24. The spring constant from the adjoining combination of
springs is
m
2K
K K
(a) K (b) 2K
(c) 4K (d) 5K/2
25. A Second’s pendulum is placed in a space laboratory
orbiting around the earth at a height 3 R from the earth’s
surface where R is earth’s radius. The time period of the
pendulum will be
(a) zero (b) 2 3
(c) 4 sec (d) infinite
26. A simple pendulum attached to the roof of a lift has a time
period of 2s in a stationary lift. If the lift is allowed to fall
freely the frequency of oscillations of pendulum will be
(a) zero (b) 2Hz
(c) 0.5Hz (d) infinity
27. Twosimple pendulumsoflength 0.5 m and 20 mrespectively
are given small linear displacement in one direction at the
same time. They will again be in the phase when the
pendulum of shorter length has completed oscillations
[nT1=(n–1)T2, where T1 is timeperiod ofshorter length &
T2 be time period of longer wavelength and n are no. of
oscillations completed]
(a) 5 (b) 1
(c) 2 (d) 3
28. A clock which keeps correct time at 20ºC, is subjected to
40ºC. If coefficient oflinear expansion of the pendulum is
12×10–6 per ºC. Howmuch will it gain or loose in time ?
(a) 10.3 seconds/day (b) 20.6 seconds/day
(c) 5 seconds/day (d) 20 minutes/day
29. A mass is suspended separately by two different springs
in successive order then time periods is t1 and t2
respectively. It is connected by both springs as shown in
fig. then time period is t0, thecorrect relation is
k1 k2
m
(a) 2
2
2
1
2
0 t
t
t +
= (b) 2
2
2
1
2
0 t
t
t -
-
-
+
=
(c) 1
2
1
1
1
0 t
t
t -
-
-
+
= (d) 2
1
0 t
t
t +
=
30. When an oscillator completes 100 oscillations itsamplitude
reduces to
3
1
ofits initial value. What will be its amplitude,
when it completes 200 oscillations ?
(a)
8
1
(b)
3
2
(c)
6
1
(d)
9
1
31. A particle of mass m is fixed to one end of a light spring of
force constant k and unstretched length l. The system is
rotated about the other end of the spring with an
angular velocity w, in gravity free space. The increase in
length of the spring will be
k
m
w
(a)
k
m 2
l
w
(b) 2
2
m
k
m
w
-
w l
(c) 2
2
m
k
m
w
+
w l
(d) None of these
32. Frequency of oscillation is proportional to
2k
k
m
(a)
m
k
3
(b)
m
k
(c)
m
k
2
(d)
k
3
m](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-363-320.jpg)


![362 PHYSICS
Exemplar Questions
1. The displacement of a particle is represented by the
equation 3cos 2 .
4
y t
p
æ ö
= - w
ç ÷
è ø
The motion of the particle
is
(a) simple harmonic with period 2p/w
(b) simple harmonic with period p/w
(c) periodicbut not simpleharmonic
(d) non-periodic
2. The displacement of a particle is represented by the
equation y = sin3 wt. The motion is
(a) non-periodic
(b) periodicbut not simpleharmonic
(c) simple harmonic with period 2p/w
(d) simple harmonic with period p/w
3. The relation between acceleration and displacement offour
particles are given below
(a) ax = +2x (b) ax = +2x2
(c) ax = –2x2 (d) ax = –2x
Which, one of the particle is exempting simple harmonic
motion?
4. Motion of an oscillating liquid column in a U-tube is
(a) periodicbut not simpleharmonic
(b) non-periodic
(c) simple harmonic and time period is independent ofthe
density of the liquid
(d) simpleharmonicand timeperiod isdirectlyproportional
to the density of the liquid
5. Aparticle isacted simultaneouslybymutuallyperpendicular
simple harmonic motion x = a cos wt and y = a sin wt. The
trajectoryof motion of the particle will be
(a) an ellipse (b) a parabola
(c) a circle (d) a straight line
6. The displacement of a particle varies with time according to
the relation sin cos .
y a t b t
= w + w
(a) The motion is oscillatory but not SHM
(b) The motion is SHM with amplitude a + b
(c) The motion is SHM with amplitude a2 + b2
(d) The motion is SHM with amplitude 2 2
a b
+
7. Four pendulums A, B, C and D are suspended from the
same
G G
D
C B A
elastic support as shown in figure. A and C are of the same
length, while B is smaller than A and D is larger than A. IfA
is given a transverse displacement,
(a) Dwill vibrate with maximum amplitude
(b) C will vibrate with maximum amplitude
(c) B will vibrate with maximum amplitude
(d) All the four will oscillate with equal amplitude
8. Figure shows the circular motion of a particle. The radius of
the circle, the period, sense of revolution and the initial
position are indicated on the figure. The simple harmonic
motion of the x-projection ofthe radius vector of the rotating
particle P is
(a)
2
( ) sin
30
t
x t B
p
æ ö
= ç ÷
è ø
y
x
B
p t
T
( = 0)
= 30s
(b) ( ) cos
15
t
x t B
p
æ ö
= ç ÷
è ø
(c) ( ) sin
15 2
t
x t B
p p
æ ö
= +
ç ÷
è ø
(d) ( ) cos
15 2
t
x t B
p p
æ ö
= +
ç ÷
è ø
9. The equation of motion of a particle is x = a cos(at)2. The
motion is
(a) periodic but not oscillatory
(b) periodic and oscillatory
(c) oscillatory but not periodic
(d) neither periodic nor oscillatory
10. A particle executing SHMmaximum speed of30 cm/s and a
maximum acceleration of 60cm/s2. Theperiod ofoscillation
is
(a) p sec (b)
2
p
sec
(c) 2p sec (d)
t
p
sec
PastYears (2013-2017) NEET/AIPMTQuestions
11. A particle of mass m oscillates along x-axis according to
equation x = a sin wt. The nature of the graph between
momentum and displacement ofthe particle is
[NEET Kar. 2013]
(a) straight line passing through origin
(b) circle
(c) hyperbola
(d) ellipse](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-366-320.jpg)
![363
Oscillations
12. The oscillation of a body on a smooth horizontal surface is
represented by the equation,
X = A cos (wt)
where X = displacement at time t
w = frequency of oscillation
Which one of the following graphs shows correctly the
variation of‘a’ with ‘t’? [2014]
(a)
a
O
T t
(b)
a
O
T t
(c)
a
O
T t
(d)
a
O
T t
13. A particle is executing SHM along a straight line. Its
velocities at distances x1 and x2 from the mean position
are V1 and V2, respectively. Its time period is [2015]
(a)
2 2
2 1
2 2
1 2
x – x
2
V – V
p (b)
2 2
1 2
2 2
1 2
V V
2
x x
+
p
+
(c)
2 2
1 2
2 2
1 2
V – V
2
x – x
p (d)
2 2
1 2
2 2
1 2
x – x
2
V – V
p
14. When two displacements represented by y1 = asin(wt) and
y2 = b cos(wt) are superimposed the motion is: [2015]
(a) simple harmonic with amplitude
a
b
(b) simple harmonic with amplitude 2 2
a b
+
(c) simple harmonic with amplitude
(a b)
2
+
(d) not a simpleharmonic
15. Aparticleisexecutingasimpleharmonicmotion.Itsmaximum
acceleration is a and maximum velocityis b.
Then its time period of vibration will be : [2015 RS]
(a)
a
b
(b)
2
b
a
(c)
2pb
a
(d)
2
2
b
a
16. A particleexecutes linear simple harmonic motion with an
amplitude of 3 cm. When the particle is at 2 cm from the
mean position, the magnitude of its velocityis equal to that
ofits acceleration. Then its time period in seconds is [2017]
(a)
5
2p
(b)
4
5
p
(c)
2
3
p
(d)
5
p
17. A spring of force constant k is cut into lengths of ratio 1 : 2
: 3. Theyare connected in series and the new force constant
is k'. Then theyare connected in parallel and force constant
is k¢¢ . Then k' : k¢¢ is [2017]
(a) 1 :9 (b) 1 : 11
(c) 1 : 14 (d) 1 : 6](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-367-320.jpg)


![366 PHYSICS
16. (a) )
2
(
T
D
1
'
,
T
2
)
D
3
(
1
r
p
=
n
pr
=
n
l
l
3
2
2
3
2
'
=
´
=
n
n
17. (b)
18. (c) Kinetic energy
2 2 2
1
( )
2
K m a y
w
= -
2
2 2 2
1 2
10 [10 5 ] 375
2 2
æ ö
= ´ ´ - =
ç ÷
è ø
erg
p
p
19. (b)
2 2
1 2
1 2
2 2
1 1
,
2 2
= Þ = = Þ =
E E
E kx x E ky y
k k
and
2 2
( )
2
1
= + Þ + =
E
E k x y x y
k
1 2
1 2
2 2 2
E E E
E E E
k k k
Þ + = Þ + =
20. (c) Time to complete 1/4th oscillation is
4
T
s. Time to
complete
8
1
th vibration from extreme position is
obtained from
t
T
2
cos
a
t
cos
a
2
a
y
p
=
w
=
= or s
6
T
t =
Sotime to complete 3/8th oscillation
=
12
T
5
6
T
4
T
=
+
21. (b) )
t
(
sin
a
y f
+
w
= ; when y = a/2,
then )
t
(
sin
a
2
a
f
+
w
=
or
6
sin
2
1
)
t
(
sin
p
=
=
f
+
w or
6
5
sin
p
So phase of two particles is p/6 and 5 p/6 radians
Hence phase difference = (5 p/6) – p/6 = 2 p/3
22. (a) sin wt = x/a and
2
2
2
a
/
x
1
t
sin
1
t
cos -
=
w
-
=
w
y= sin (wt + p/4)
= sin wt cos p/4 + cos wt sin p/4
=
2
1
a
/
x
1
2
1
a
x 2
2
´
÷
ø
ö
ç
è
æ
-
+
´
or 2
2
x
a
x
y
2 -
+
=
or 2
2
2
2
2
2
x
a
x
2
)
x
a
(
x
y
2 -
+
-
+
=
=
2
2
2
x
a
x
2
a -
+
It is an equation of an ellipse.
23. (b) Let k be the force constant of spring of length l2.
Since l1 = n l2, where n is an integer, so the spring is
made of (n + 1) equal parts in length each of length l2.
k
)
1
n
(
K
1 +
= or k = (n + 1) K
The spring of length l1 (= n l2) will be equivalent to n
springs connected in series where spring constant
n
/
K
)
1
n
(
n
k
k +
=
=
¢ & spring constant of length l2
isK(n+1).
24. (c) Here all the three springs are connected in parallel to
mass m. Hence equivalent spring constant
k = K + K+ 2 K= 4 K.
25. (d) The second pendulum placed in a space laboratory
orbiting around the earth is in a weightlessness state.
Hence g = 0 so T = ¥
26. (a) When lift is falling freely, the effective acceleration
due to gravity inside the lift is zero i.e. g' = g – g = 0.
Therefore time period will be infinityand frequencyis
zero
27. (b) Let T1, T2 be the time period of shorter length and
longer length pendulums respectively.As per question,
n T1 = (n – 1) T2 ;
so
g
20
2
)
1
n
(
g
5
.
0
2
n p
-
=
p
or 6
)
1
n
(
40
)
1
n
(
n -
»
-
=
Hence n = 6/5 » 1
28. (a)
g
2
T
l
p
= ; 1/ 2
T 1
2 ( / g) /
T 2
-
D
= p ´ ´ D
l l l
)
g
2
T
T
(
l
l
Q
D
+
p
=
D
+
q
D
a
=
D
=
D
2
1
2
1
T
T
l
l
=
5
6
10
12
)
20
40
(
10
12
2
1 -
-
´
=
-
´
´
´
5
10
12
T
T -
´
´
=
D = 24 ×60× 60× 12 ×10–5
= 10.3 s/day
29. (b)
1
1
k
m
2
t p
= or
1
2
2
1
k
m
4
t
p
= or 2
1
2
1
t
m
4
k
p
=
Similarly, 2
2
2
2
t
m
4
k
p
= and
2
0
2
2
1
t
m
4
)
k
k
(
p
=
+
2
2
2
2
1
2
2
0
2
t
m
4
t
m
4
t
m
4 p
+
p
=
p
or 2
2
2
1
2
0 t
1
t
1
t
1
+
=
30. (d) It is a damped oscillation, where amplitude of
oscillation at time t is given by γ t
0
A a e-
=
where a0 = initial amplitude of oscillation
g = damping constant.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-370-320.jpg)
![367
Oscillations
As per question, γ 100 / ν
0
0
a
a e
3
-
= ……(i)
(where n is the frequency of oscillation)
and γ 200 / ν
0
A a e-
= ……(ii)
From (i) ; γ 100/ ν
o
0
a
a e
3
- ´
= ……(iii)
Dividing equation (ii) by(iii), wehave
γ 200 / ν
γ 100 / ν
0
A e
a (1/ 3) e
-
- ´
= =
γ 100 / ν 1
e
3
- ´
=
or 0
0 a
9
1
3
1
3
1
a
A =
´
´
=
31. (b) Let x = the increase in the length of spring. Then the
particle moves along a circular path of radius (l + x),
and the spring force = kx = centripetal force
mw2 (l+ x) =kx or
2
2
m
k
m
x
w
-
w
=
l
32. (a)
k k
2
x
Let mass is displaced towards left by x then force on
mass = – kx –2kx = – 3kx
[negative sign is taken because force is opposite to
the direction of motion]
F 3kx
Þ = - x
m 2
w
-
=
3k
.
m
Þ w =
1 3k
f .
2 2 m
w
= =
p p
Thus it is propotional to m
/
k
3
33. (a) Maximum velocity can be found out by energy
conservation.
2
mv
2
1
mgh = gh
2
v
or max = ;
2
gh
'
v
2
vmax
=
=
'
mgh
)
'
v
(
m
2
1
mgh 2
+
= ;
'
mgh
2
mgh
2
1
mgh +
=
Þ '
mgh
4
mgh
3
=
4
h
3
'
h
or =
34. (b) Loss in PE of mass = gain in PE of the spring
mg(h + x) =
2
kx
2
1
2
kx – 2mgx – 2mgh = 0
Þ x=
k
2
)
mgh
2
(
k
4
g
m
4
mg
2 2
2
-
-
±
or x=
k
mgh
2
k
g
m
k
mg
2
2
2
+
±
x = A–
k
mg
=
k
mg
k
mgh
2
k
g
m
2
2
2
-
+
=
k
mg
ú
ú
û
ù
ê
ê
ë
é
-
+ 1
mg
kh
2
1
35. (a) t = 0, v maximum. The motion begins from mean
position. So it represents S.H.M.
36. (a) The both of the pendulum will more along a straight
lineAB.
q q
Re
mg
x
A B
The direction ofthe Earth's gravitational field is radial
Now, mg
R
m
GM
F 2
e
e
=
=
x
R
m
GM
R
x
F
cos
F
F 3
e
e
e
x -
=
-
=
q
-
= =–kx
where
e
3
e
GM m
k
R
=
Time period ofa simple harmonic oscillator,
3
e
e R
/
m
GM
m
2
k
m
2
T p
=
p
=
or
g
R
2
R
GM
R
2
T e
2
e
e
e
p
=
p
=
37. (a) For the block is about to slip, a
g 2
w
=
m
or
g
a
m
Þ w =
g 1 g
2 ν ν
a 2 a
m m
Þ p = Þ =
p
38. (d) Oscillations along spring length are independent of
gravitation.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-371-320.jpg)
![368 PHYSICS
39. (c )
2 2
1 4
I M(2L) ML
3 3
= =
Force applied by the spring is F = – kx
Þ F = – k (2Lq)
(q is the angular displacement from the equilibrium
position). Further
2 2
| F | 4L ksin 4L k
t = ´ = q = - q
r r
l
Also,
..
2
I I 4L k
t = a = q = - q
Þ
.. 3k
0
M
q+ q =
Þ 0
3k
M
w =
40. (a) V(x)=k |x|3
since, 2
dV(x)
F 3k | x |
dx
= - = - ……(i)
x = a sin (wt)
This equation always fits to the differential equation
2
2
2
d x
x
dt
= -w or
2
2
d x
m m x
dt
= - w
Þ F = – mw2x ……(ii)
Equations (i) and (ii) give
2 2
3k | x | m x
- = - w
Þ 1/ 2
3kx 3ka
[sin( t)]
m m
w = = w
Þ a
wµ
Þ
1
T
a
µ
41. (b)
2R
T 2 2
g g
= p = p
l
42. (d) Let the extension in the spring be x0 at equilibrium. If
F0 be the tension in the string then F0 = kx0. Further if
T0 is the tension in the thread then T0 = mg and
2T0 =kx0.
Let the mass m be displaced through a slight
displacement x downwards. Let the the new tension in
the string and spring be T and F respectively.
Þ 0
x
F x
2
æ ö
= ç ÷
è ø
and F = 2T
Þ 0
x
2T k x
2
æ ö
= ç ÷
è ø
Þ 0
kx
(T T )
4
- =
Þ Time period
m m
2 4
k k
4
= p = p
43. (b)
2
1
mg(h y) ky
2
+ =
Þ
mg mg 2kh
y 1
k k mg
= ± +
At equilibrium
mg = ky0
Þ 0
mg
y
k
=
Þ Amplitude A = y – y0
mg 2kh
1
k mg
= +
Energyof oscillation is
2
2
1 mg
E kA mgh
2 2k
æ ö
= = + ç ÷
è ø
44. (b) For block Ato move in S.H.M.
mg x
N
A
mean
position
mg–N =mw2x
where x is the distance from mean position
For block to leave contact N = 0
2
2 g
x
x
m
mg
w
=
Þ
w
=
Þ
45. (a) The displacement of a particle in S.H.M. is given by
y= a sin (wt + f)
velocity=
dy
dt
= wa cos (wt + f)
The velocity is maximum when the particle passes
through the mean position i.e.,
max
dy
dt
æ ö
ç ÷
è ø = w a](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-372-320.jpg)
![369
Oscillations
The kinetic energy at this instant is given by
1
2
m
2
max
dy
dt
æ ö
ç ÷
è ø =
1
2
mw2 a2 = 8 × 10–3 joule
or
1
2
× (0.1) w2 × (0.1)2 = 8 × 10–3
Solving we get w= ±4
Substituting the values of a, w and f in the equation of
S.H.M., we get
y= 0.1 sin (± 4t + p /4) metre.
46. (d) Slope of F - x curve = – k =
80
0.2
- Þ k = 400 N/m,
Timeperiod, T = 2p
m
k
= 0.0314 sec.
47. (b) At resonance, amplitude ofoscillation is maximum
Þ 2w2 –36w+ 9 isminimum
Þ 4w– 36 = 0 (derivative is zero)
Þ w= 9
48. (b) Torque about hinge
2.5 g × 0.40 cos q – 1g × 1 cos q = 0
49. (c) 50. (b)
EXERCISE - 3
Exemplar Questions
1. (b) As given that, 3cos 2
4
y t
p
æ ö
= - w
ç ÷
è ø
Velocityof the particle
3cos 2
4
dy d
v t
dt dt
é p ù
æ ö
= = - w
ç ÷
ê ú
è ø
ë û
3( 2 ) sin 2
4
t
é p ù
æ ö
= - w - - w
ç ÷
ê ú
è ø
ë û
6 sin 2
4
t
p
æ ö
= w - w
ç ÷
è ø
So, acceleration,
6 sin 2
4
dv d
a t
dt dt
é p ù
æ ö
= = w - w
ç ÷
ê ú
è ø
ë û
(6 ) ( 2 )cos 2
4
t
p
æ ö
= w ´ - w - w
ç ÷
è ø
2
4 3cos 2
4
t
é p ù
æ ö
= - w - w
ç ÷
ê ú
è ø
ë û
2
4
a y
= - w
In simple harmonic motion acceleration (or force) is
directly proportional to the negative of displacement
ofparticle
Þ as acceleration, a y
µ -
Hence, due to negativesign motion is simple harmonic
motion (SHM.)
Asimpleharmonic motion isalwaysperiodic. Somotion
is periodic simpleharmonic.
From the given equation,
3cos 2
4
y t
p
æ ö
= - w
ç ÷
è ø
Compare it by standard equation
cos( )
y a t
= w + f
So, ' 2
w = w
2 2
2 '
' 2
T
T
p p p
= w Þ = =
w w
Hence, the motion is SHM with period
p
w
.
2. (b) A motion will be harmonic if a µ displacement and a
simple harmonic motion is always periodic but all
simple harmonic motion are periodic but all periodic
are not harmonic.
As given equation of motion is
3
sin
y t
= w
(3sin 4sin3 )/ 4
t t
= w - w
3
[ sin3 3sin 4sin ]
q = q- q
Q
Differentiating both side w.r.t. t
So, (3sin ) (4sin3 ) / 4
dy d d
v t t
dt dt dt
é ù
= = w - w
ê ú
ë û
or
3 (3sin sin3 )
sin
4
q - q
é ù
q = ê ú
ë û
4 3 cos 4 [3 cos3 ]
dy
t t
dt
= w w - ´ w w
Again, differentiating both side w.r.t. t
2
2
2
4 3 sin 36 sin3
d y
t t
dt
´ = - w w + w w
2 2
2
3 sin 36 sin3
4
d y t t
a
dt
- w w + w w
= =
So,
2
2
d y
dt
æ ö
ç ÷
ç ÷
è ø
is not directly proportional to y.
Somotion is not harmonic.
3
( ) sin ,
y t t
= w
3
( ) sin ( )
y t T t T
+ = w +
3 2
sin ( )
t T
T
p
é ù
= +
ê ú
ë û
3 3
sin (2 ) sin
t t
= p + w = w](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-373-320.jpg)
![370 PHYSICS
3. (d) For motion to be SHM acceleration of the particle must
be opposite of restoring force and proportional to
negative of displacement. So, F = ma = m(–2x)
i.e., F = –2mx, so F x
µ -
Hence, ax = –2x
We should be clear that x has to be linear.
4. (c) Consider a U-tube filled in which a liquid column
oscillates. When liquid column lifted upto height y
from A toB in arm Q. The liquidlevel in arm Pbecomes
at C', so the difference between the height of two
columns are = AB +A'C = y + y = 2y.
In this case, restoring force acts on the liquid due to
gravity. Acceleration of the liquid column, can be
calculated in terms of restoring force.
P Q
B
A
C
B'
A'
C'
h
y
Equilibrium level
Restoring force,
f = Weight of liquid column of height 2y
( 2 ) 2
f A y g A gy
= - ´ ´r ´ = - r
[ ]
v
h =r
Q
As restoring force at A opposite to gravitational force
as liquid is lifted against ( ) 2
t mg k A g
w m = r
Then f y
µ - so motion is SHM.
Timeperiod
(2 )
2 2 2
2
m A h h
T
k A g g
´ ´r
= p = p = p
r
2
h
T
g
= p
Time period is independent ofthe density of the liquid
and motion is harmonic.
5. (c) The resultant-displacement can be find by adding x
and y-components.
According to variation of x and y, trajectory will be
predicted, so resultant displacement is y' = (x + y)
As given that,
cos
x a t
= w ...(i)
sin
y a t
= w ...(ii)
So, ' ( cos sin )
y a t a t
= w + w
' (cos sin )
y a t t
Þ = w + w
cos sin
' 2
2 2
t t
y a
w w
é ù
= +
ê ú
ë û
' 2(cos cos 45 sin sin 45 )
y a t t
= w °+ w °
2 cos( 45 )
a t
= w - °
So, the displacement is not straight line and not
parabola also.
Now, squaring and adding eqs. (i) and (ii),
2 2 2
x y a
+ = 2 2
[ cos sin 1]
t t
w + w =
Q
This is the equation of a circle, so motion in circular
(independent of time).
Clearly, the locus is a circle of constant radius a.
6. (d) As given that, the displacement is
sin cos
y a t b t
= w + w
Let sin
a A
= f ...(i)
and cos
b A
= f ...(ii)
Squaring and adding (i) and (ii)
2 2 2 2 2 2
sin cos
a b A A
+ = f+ f
2 2
A a b
= + (amplitude)
sin sin cos cos
y A t A t
= f× w + f w
cos( )
y A t
= w - f
sin( )
dy
A t
dt
= - w w - f
2
2 2
2
cos( )
d y
A t y
dt
= - w w - f = -w
Thus,
2
2
( )
d y
y
dt
µ - so, motion is SHM.
Hence, it is an equation of SHM with amplitude
2 2
.
A a b
= +
7. (b) When pendulum vibrate with transverse vibration then
2
l
T
g
= p
l = length of pendulum.
G G
Elastic support
A
B
C
D
e
Through the elastic rigid support the disturbance is
transferred to all the pendulum A and C are having
length and hence same frequency. They will be in
resonance, because their time period of oscillation.
So, a periodic force of period (T) produces resonance
in AandCandtheywillvibratewith maximumamplitude
as in resonance.](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-374-320.jpg)
![371
Oscillations
8. (a) As the particle (P) is executing circular motion with
radius B.
Let particle P is at Q at instant any (t), foot of
perpendicular on x axis is at R vector OQ makes Ðq ,
with its zero position not P displacement of particles
for O to R.
Consider angular velocity of the particle executing
circular motion is w and when it is at Q makes and
angle q as shown in the diagram.
BR
x
y
p t
( =0)
Q
q
q
r
90–q
O
Clearly, t
q = w
Now, we can write
cos(90 – )
OR OQ
= q ( )
OR X
=
Q
sin sin
x OQ OQ t
= q = w
sin
r t
= w [ ]
OQ r
=
Q
2 2
sin sin
30
x B t B t
T
p p
æ ö
= = ç ÷
è ø
2
sin
30
x B t
p
æ ö
= ç ÷
è ø
Hence, this equation represents SHM.
9. (c) According to the question,
2
cos( )
x a t
= a
is a cosine function, so it is an oscillatory motion.
Now, at, t = (t + T). The equation of motion of particle
2
( ) cos[ ( )]
x t T a t T
+ = a + 2
[ ( ) cos( ) ]
x t a t
= a
Q
2 2
cos[ 2 ] ( )
a t T tT x t
= a + a + a ¹
where, T is supposed as period of the function w(t).
Hence, it is oscillatory but not periodic.
10. (a) Let us consider a equation of an SHM is represented
by y = a sin wt
cos
dy
v a t
dt
= = w w
max
( ) 30 cm/sec
v a
= w = (given)...(i)
Acceleration 2
( ) sin
= = - w w
dv
a a t
dt
2
max 60
= w =
a a (given)...(ii)
Eqs. (i) and (ii), we get
( ) 60 (30) 60
a
w w = Þ w =
w= 2 rad/s
2
2 rad/s
T
p
=
sec
= p
T
PastYears (2013-2017) NEET/AIPMTQuestions
11. (d) As
2 2
2 2 2
1
v y
a a
+ =
w
This is the equation of ellipse.
Hence the graph is an ellipse. P versus x graph is
similar to V versus x graph.
12. (c) Displacement, x = Acos (wt) (given)
Velocity, v =
dx
A sin ( t)
dt
= - w w
Acceleration, a = 2
dv
A cos t
dt
= - w w
Hence graph (c) correctly dipicts the variation of a
with t.
13. (a) As we know, for particle undergoing SHM,
2 2
V A – X
= w
2 2 2 2
1 1
V (A – x )
=w
2 2 2 2
2 2
V (A – x )
=w
Substracting we get,
2 2
2 2
1 2
1 2
2 2
V V
x x
+ = +
w w
Þ
2 2
2 2
1 2
2 1
2
V – V
x – x
=
w
Þ
2 2
1 2
2 2
2 1
V – V
w
x – x
=
Þ
2 2
2 1
2 2
1 2
x – x
T 2
V – V
= p
14. (b) The two displacements equations are y1 = a sin(wt)
and y2 = b cos(wt) = b sin t
2
p
æ ö
w +
ç ÷
è ø
yeq = y1 + y2
= a sinwt + b coswt = a sinwt + b sin t
2
p
æ ö
w +
ç ÷
è ø
Since the frequencies for both SHMs are same,
resultant motion will be SHM.
NowAeq =
2 2
a b 2ab cos
2
p
+ +
b
a
2 2
eq
A a b
Þ = +](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-375-320.jpg)



![376 PHYSICS
By comparison of the standard equation to above given
equation,
we get .
sec
10
1000
1
T 3
-
=
=
Particle velocity
÷
ø
ö
ç
è
æ p
-
p
p
´
p
=
=
17
x
t
2000
cos
2000
10
dt
dy
s
/
m
200
s
/
cm
000
,
20
dt
dy
max
=
=
÷
ø
ö
ç
è
æ
Þ (as vmax = A
Aw)
Example2.
A progressive wave of frequency 500 Hz is travelling with
a velocity of 360 m/s. Howfar apart are two points 60o out
of phase?
Solution :
We known that for a wave v = f l
so l=
v 360
f 500
= = 0.72 m
Now as in a wave path difference is related to phase
difference by the relation.
Phase difference Df= 60o = (p/180) x 60 = (p/3) rad
Path difference Dx=
2
l
p
(Df)=
0.72
2 3
p
p
= 0.12 m
Example3.
Determine the change in volume of 6 litres of alcohol if
the pressure is decreased from 200 cm of Hg to 75 cm.
[velocity of sound in alcohol is 1280 m/s, density of
alcohol = 0.81 gm/cc, density of Hg = 13.6 gm/cc and
g = 9.81 m/s2].
Solution :
For propagation of sound in liquid
v = ( )
B / r , i.e., B = v2r
But by definition B= – V
P
V
D
D
so –V
P
V
D
D
= v2r, i.e., DV = 2
V( P)
v
-D
r
Here DP = H2rg – H1rg = (75 – 200) ´ 13.6 ´ 981
= –1.667 ´ 106 dyne/cm2
so DV =
( )( )
( )
3 6
2
5
6 10 1.667 10
0.81 1.280 10
´ ´
´ ´
= 0.75 cc
Example4.
(a) Speed of sound in air is 332 m/s at NTP. What will be
the speed of sound in hydrogen at NTP if the density
of hydrogen at NTP is (1/16) that of air?
(b) Calculate the ratio of the speed of sound in neon to that
in water vapour at any temperature. [Molecular weight of
neon = 2.02 ´ 10–2 kg/mol and for water vapours = 1.8 ´
10–2 kg/mol]
Solution :
The velocity of sound in air is given by
v =
E
r
=
P
g
r
=
RT
M
g
(a) In terms of density and pressure
H
air
v
v =
air
H
H air
P
P
r
´
r =
air
H
r
r [as Pair = PH]
or vH = vair ´
air
H
r
r = 332 ´
16
1
= 1328 m/s
(b) In terms of temperature and molecular weight
Ne
W
v
v =
Ne W
Ne W
M
M
g
´
g [as TN = TW]
Now as neon is monatomic (g = 5/3) while water vapours
polyatomic (g = 4/3) so
Ne
W
v
v =
( )
( )
2
2
5 / 3 1.8 10
4 / 3 2.02 10
-
-
´ ´
´ ´
=
5 1.8
4 2.02
´ = 1.05
BEATS
When two wave trains slightly differing in frequencies travel
along the same straight line in the same direction, then the
resultant amplitude is alternately maximum and minimum at a
point in the medium. This phenomenon of waxing and waning
of sound is called beats.
Let two sound waves of frequencies n1 and n2 are propagating
simultaneouslyand in same direction. Then at x=0
y1 = A sin 2p n1t, and y2 = A sin 2p n2t,
For simplicity we take amplitude of both waves to be same.
By principle of superposition, the resultant displacement at any
instant is
y = y1 + y2 = 2A cos 2p nAt sin 2p navt
where
2
n
n
n 2
1
av
+
= ,
2
n
n
n 2
1
A
-
=
Þ y = Abeat sin 2p navt ..................(i)
It is clear from the above expression (i) that](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-380-320.jpg)

![378 PHYSICS
Solution :
In this case, we can assume that both the source and
observer are moving towards each other with velocityv. If
c be the velocity of signal, then
n
v
c
v
c
n ÷
ø
ö
ç
è
æ
-
+
=
¢ or n
)
v
c
(
)
v
c
(
)
v
c
(
n
2 ÷
÷
ø
ö
ç
ç
è
æ
-
-
+
=
¢
or
2 2 2
2 2 2
(c v ) c
n n n; (as c v)
c v 2c v c 2cv
-
¢ ¢
= Þ = >>
+ - -
n
v
2
c
c
n ÷
÷
ø
ö
ç
ç
è
æ
-
=
¢
STATIONARY OR STANDING WAVES
When two progressive waves having the same amplitude, velocity
and time period but travelling in opposite directions
superimpose, then stationary wave is produced.
Let two waves ofsame amplitude and frequencytravel in opposite
direction at same speed, then
y1 = Asin (wt –kx) and
y2 = Asin (wt + kx)
By principle of superposition
y = y1 + y2 = (2A cos kx) sin wt ...(i)
s
y A sin ωt
=
It is clear that amplitude ofstationary waveAs varywith position
(a) As = 0, when cos kx = 0 i.e., kx = p/2, 3p/2............
i.e.,x =l/4, 3l/4...................[ask=2p/l]
These points are called nodes and spacing between two
nodes is l/2.
(b) As is maximum, when cos kx is max
i.e., kx= 0,p,2p,3pi.e.,x=0,ll/2,2l/2....
It is clear that antinode (where As is maximum) are also
equally spaced with spacing l/2.
(c) The distance between node and antinode is l/4 (see figure)
Antinode Antinode
segment 1 segment 2 segment 3
Node
x
l
l
/2
/4
o
2A
Keep in Memory
1. When a string vibrates in one segment, the sound produced
is called fundamental note. The string is said to vibrate in
fundamental mode.
2. The fundamental note is called first harmonic, and is given
by
l
2
v
0 =
n , where v = speed of wave.
3. If the fundamental frequencybe 0
n then 2 0
n , 3 0
n , 4 0
n
... are respectively called second third, fourth ... harmonics
respectively.
4. If an instrument produces notes of frequencies
4
3
2
1 ,
,
, n
n
n
n .... where 1 2 3 4
ν ν ν ν
< < < ....., then 2
n is
(ii) If source and observer both move towards each other.
0
3 0
s
V V
V V
æ ö
+
¢
n = n
ç ÷
-
è ø
;
Whenthewindblows inthedirection of sound, then in all above
formulaeVisreplacedby(V+ W) whereWis thevelocityofwind.
Ifthe wind blowsin theoppositedirectiontosoundthenVisreplaced
by(V– W).
Keep in Memory
1. The motion of the listener causes change in number of
waves receivedbythe listener andthis producesan apparent
change in frequency.
2. The motion of the source of sound causes change in
wavelength of the sound waves, which produces apparent
change in frequency.
3. If a star goes away from the earth with velocity v, then the
frequencyof the light emitted from it changes from n ton'.
n' = n (1–v/c), where c is the velocity of light and
or
v v
c c
Dn Dl
= =
n l
where l
D is called Doppler’s shift.
If wavelength of the observed waves decreases then the
object from which the waves are coming is moving towards
the listener and vice versa.
Example7.
Two engines cross each other travelling in opposite
direction at 72 km/hour. One engine sounds a whistle of
frequency 1088 cps. What are the frequencies as heard by
an observer on the other engine before and after crossing.
Take the speed of sound as 340 m/s.
Solution :
The apparent frequency before crossing,
÷
÷
ø
ö
ç
ç
è
æ
-
+
=
¢
s
0
v
v
v
v
n
n
HereVo = 72 km/hour = 20 m/s
vs = 72 km/hour = 20 m/s
÷
ø
ö
ç
è
æ
-
+
´
=
¢
20
340
20
340
1088
n Hz
1224
320
360
1088 =
´
=
The apparent frequency after crossing
0
s
v v
n'' n
v v
æ ö
-
= ç ÷
+
è ø
÷
ø
ö
ç
è
æ
+
-
´
=
20
340
20
340
1088
Hz
11
.
967
36
32
1088 =
´
=
Example8.
A rocket is going towards moon with a speed v. The
astronaut in the rocket sends signals of frequency n
towards the moon and receives them back on reflection
from the moon. What will be the frequency of the signal
received by the astronaut? (Take v << c)](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-382-320.jpg)
![379
Waves
called first overtone, 3
n is called second overtone, 4
n is
called third overtone ... so on.
5. Harmonics are the integral multiples of the fundamental
frequency.If n0 be the fundamental frequency, then 0
nn is
the frequencyof nth harmonic.
6. Overtones are the notes of frequency higher than the
fundamental frequencyactuallyproduced bythe instrument.
7. In the strings all harmonics are produced.
StationaryWaves in an Organ Pipe :
In the open organ pipe all the harmonics are produced.
In an open organ pipe, the fundamental frequency or first
harmonic is 0
2
v
n =
l
, where v is velocity of sound and l is the
length of air column [see fig. (a)]
(a)
l
(b)
l
2
l
=
l ,
1
2l
=
l
2
2l
=
l ,
2
2l
=
l
(c)
l
2
3l
=
l ,
3
L
3
=
l
Similarly the frequency of second harmonic or first overtone is
[see fig (b)], 01
2
2
v
n =
l
Similarly the frequency of third harmonic and second overtone
is, [(see fig. (c)] 02
3
2
v
n =
l
Similarly 03 04
4 5
,
2 2
v v
n n
= =
l l
..................
In the closed organ pipeonlythe odd harmonics are produced. In
a closed organ pipe, the fundamental frequency (or first
harmonic) is (see fig. a)
4
c
v
n =
l
(a)
l
(b)
l
(c)
l
4
l
=
l
4
3l
=
l
4
5l
=
l
Similarly the frequencyof third harmonic or first overtone (IInd
harmonic absent) is (see fig. b)
l
4
v
3
n 2
c =
Similarly
l
l 4
v
7
n
,
4
v
5
n 4
c
3
c =
= ........
End Correction
It is observed that the antinode actually occurs a little above the
open end. A correction is applied for this which is known as end
correction and is denoted bye.
(i) For closed organ pipe : l is replaced by l+ e where
e = 0.3D, D is the diameter of the tube.
(ii) For open organ pipe: l is replaced by l + 2e where
e=0.3D
In resonance tube, the velocity of sound in air given by
( )
2 1
2ν
v l l
= -
where n = frequency of tuning fork, ll = 1st resonating
length, l2 = 2nd resonating length.
ResonanceTube :
It is used to determine velocity of sound in air with the help of a
tuning fork of known frequency.
n n
A
e
l
1
e
l
2
Let l1 and l2 are lengths of first and second resonances then
1 e
4
l
+ =
l and 2
3
e
4
l
+ =
l
2 1
2
l
Þ - =
l l 2 1
2( )
Þ l = -
l l
Speed of sound in air is
v = ul where u is the frequency
2 1
2 ( )
v = u -
l l](https://image.slidesharecdn.com/dishaneetphysicsguide-240427161812-19b55928/85/Disha-NEET-Physics-Guide-for-classes-11-and-12-pdf-383-320.jpg)