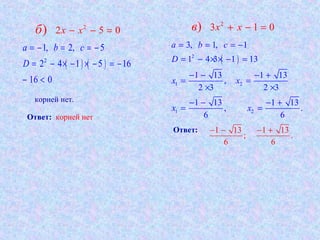Документ рассматривает методы решения квадратных уравнений и включает в себя примеры задач из древнего Египта и Вавилона. Представленные уравнения и их решения демонстрируют использование дискриминанта и формулы корней, способы определения количества корней. В качестве примеров приводятся конкретные уравнения и шаги их решения, включая различные сценарии для дискриминанта.

1. Формулы для решенияФормулы для решения
квадратных уравненийквадратных уравнений
(Повторение)(Повторение)1010 класскласс

2. Задача из Древнего ЕгиптаЗадача из Древнего Египта
« Найти стороны поля, имеющего« Найти стороны поля, имеющего
форму прямоугольника, если егоформу прямоугольника, если его
площадь 12, а ¾ длины равныплощадь 12, а ¾ длины равны
ширине»ширине»

3. В одной из вавилонских задач такВ одной из вавилонских задач так
же требовалось определить длину пря-же требовалось определить длину пря-
моугольного поля и его ширину :моугольного поля и его ширину :
«Сложив длину и две ширины прямо-«Сложив длину и две ширины прямо-
угольного поля, получишь 14, а пло-угольного поля, получишь 14, а пло-
щадь поля 24. Найди его стороны».щадь поля 24. Найди его стороны».

4. Составим систему уравненийСоставим систему уравнений
2 14
24
x y
xy
+ =

=
24
24xy y
x
= ⇒ =
2
24
2 14
48
14
14 48 0
x
x
x
x
x x
+ × =
+ =
− + =
( )
22 2 2 2
14 2 7 7 7 7 49x x x x x− = − × × + − = − −

5. Теперь уравнение можно записать так:
( )
( )
2
2
7 49 48 0
7 1.
x
x
− − + =
− =
7 1
8
x
x
− =
=
Мы пришли к квадратному уравнению, которое умели
решать и египтяне. Не зная отрицательных чисел,
древние математики получали:
28
3.
8
y = =
Т.е. длина поля равна 8, а ширина поля равна 3.

6. 2
0ax bx c+ + =
2
4D b ac= −
- дискриминант
квадратного уравнения
Возможны 3 случая:
0D < - корней нет
0D = - один корень
2
0
2
0
2
2
b
x
a
b
x
a
b
x
a
 
+ = ÷
 
+ =
= −

7. №1. Решите уравнения:
0D > - два корня
2
b D
x
a
− ±
=
2
2 3 5 0) x xa + − =
2, 3, 5a b c= = = −
( )2
3 4 2 5 49D = − × × − =
1 2
3 7 3 7
,
2 2 2 2
x x
− − − +
= =
× ×
1 2
10 4
,
4 4
x x
−
= =
1 2
5
, 1.
2
x x= − = 5
; 1.
2
−Ответ:

8. ( ) ( )2
1, 2, 5
2 4 1 5 16
16 0
a b c
D
= − = = −
= − × − × − = −
− <
2
2 5 0) x xб − − =
2
3 1 0) x xв + − =
Ответ: корней нет
корней нет.
( )2
1 2
1 2
3, 1, 1
1 4 3 1 13
1 13 1 13
,
2 3 2 3
1 13 1 13
, .
6 6
a b c
D
x x
x x
= = = −
= − × × − =
− − − +
= =
× ×
− − − +
= =
Ответ: 1 13 1 13
; .
6 6
− − − +

9. №2. Вычислите дискриминант квадратного уравнения.
2
2 3 0) x xa + − =
2
2 5 8 0) x xб + + =
2
2 2 0) x xв − + =
( )
2
2
1, 2, 3
2 4 1
0
6
2 3
3 1
)
a b c
D
x xa
= = = −
= − × × −
+
=
− = 2
2
2, 5
2 5 8 0
, 8
5 4 2 8 39
)
a b c
x x
D
б
= = =
+
= − × × = −
+ =
( )
2
2
1, 2, 2
2 4 1 2 12
2 2 0)
a b c
D
x xв
= − = =
= − × − ×
=
=
− +
Ответ: 16.
Ответ: - 39.
Ответ: 12.

10. №3. Определите количество корней квадратного
уравнения.
Вопрос: От чего зависит количество корней квадратного уравнения?
2
3 5 0) x xa + − =
2 1
9 2 0
9
) x xб − + =
2
5 0) x xв − + − =
( )2
2
3, 1, 5
1 4 3 5
1 60 6
3 5
1
0
0
61
)
a b c
D
два к р
x
о ня
xa
= = = −
= − × × − =
= + =
>
+ − =
( )
2
2
1
9, 2,
9
1
9 2
1
2 4 9
9
9
4 4 0
0) x x
a b c
D
один корень
б
= = − =
= − − × × =
= − =
− + =
Ответ: 2 корня.
Ответ: 1 корень.

11. ( ) ( )
2
2
1, 1, 5
1 4 1 5
1 20 19
19 0
5 0)
a b c
D
нет к
x x
орней
в
= − = = −
= − × − × − =
= − = −
− <
− + − =
Ответ: нет корней
№4. Решите квадратное уравнение:
2
12 0) x xa + − =
2
2 9 5 0) x xб + − =
2
0,8 4 5 0) x xв − + =
2
20 21 4 0) x xг − + =

12. ( )2
1 2
1 2
1
2
2
1, 1, 12
1 4 1 12 49
1 7 1 7
,
2 1 2 1
8 6
,
2 2
4, 3.
: 4;
12
.
0
3
)
a b c
D
x x
x x
x x
Отв
x
ет
xa
= = = −
= − × × − =
− − − +
= =
× ×
−
= =
= − =
−
+ − =
( )
2
2
1 2
2
2
1
1
2, 9, 5
9 4 2 5 121
9 11 9 11
,
2 2 2
2
2
20 2
,
4 4
1
5, .
2
1
: 5
2
9 5 0
; .
)
a b c
D
x x
x x
x x
Отве
x
т
xб
= = = −
= − × × − =
− − − +
= =
× ×
−
= =
= − =
−
+ − =
( )
2
2
0,8, 4, 5
4 4 0,8 5 0
0,8 4 5 0
4
2 0,8
4
1,6
2,5
: 2,5.
)
a b c
D
x
x
x
О
x x
твет
в
= = − =
= − − × × =
=
×
=
=
− + =
( )
2
1 2
1 2
2
1 2
20, 21, 4
21 4 20 4 121
21 11 21 11
,
2 20 2 20
10 32
,
40 40
1
, 0,
20 2
8.
4
1
: ; 0,8.
4
1 4 0)
a b c
D
x x
x x
x x
Отве
x
т
xг
= = − =
= − − × × =
− +
= =
×
−
×
+ =
= =
= =

13. Формула корней квадратного уравненияФормула корней квадратного уравнения
с четным вторым коэффициентомс четным вторым коэффициентом
2
0
2
ax bx c
b kчетное число
+ + =
= −
2
k k ac
x
a
− ± −
=