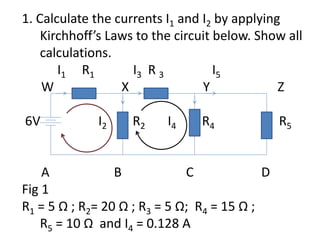
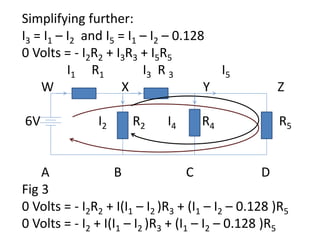
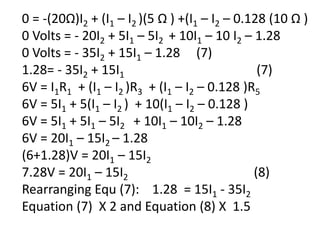This document discusses calculating currents in an electrical circuit using Kirchhoff's laws. It provides the circuit diagram and component values. It then shows calculations using Kirchhoff's current law and voltage law to find the unknown currents I1 and I2. Three different methods are presented that calculate I1 = 0.496 A and I2 = 0.176 A by setting up loop equations and solving simultaneously.

1. FET College Registrations
& Matric Rewrite
Matric Rewrite: Old, New & Technical
Matric
Mechanical Engineering N1 – N6
Electrical Engineering N1 – N6
Civil Engineering N1 – N6
Business Qualifications N4 – N6
Phone: 073 090 2954
Fax: 011 604 2771
Email: mathsmech206@gmail.com

2. FET College Registrations
& Matric Rewrite
Matric Rewrite: Old, New & Technical
Matric
Mechanical Engineering N1 – N6
Electrical Engineering N1 – N6
Civil Engineering N1 – N6
Business Qualifications N4 – N6
Phone: 073 090 2954
Fax: 011 604 2771
Email:

3. Industrial Electronics N3
Kirchhoff’s Laws
Current Law
Voltage Law
Calculations and Problems

4. 1. Calculate the currents I1 and I2 by applying
Kirchhoff’s Laws to the circuit below. Show all
calculations.
I1 R1 I3 R 3 I5
W X Y Z
6V I2 R2 I4 R4 R5
A B C D
Fig 1
R1 = 5 Ω ; R2= 20 Ω ; R3 = 5 Ω; R4 = 15 Ω ;
R5 = 10 Ω and I4 = 0.128 A

5. Kirchhoffs’ Current Law states that the sum of the
currents entering a node is equal to the sum
of the currents leaving that node.
Based on this definition, we shall apply
Kirchhoffs’ Current Law to the following
nodes:
Node X: I1= I2 + I3
Re arranging , we have: I3 = I1 – I2 (1)
Node C : I3 = I4 + I5
Re arranging , we have: I5 = I3 – I4 (2)
Considering the fact that I3 = I1 – I2,
I4 =0.128 and substituting these values into (2)
: I5 = I1 – I2 – 0.128 (3)

6. Kirchhoffs’ Voltage Law states that the sum of the
voltage drops in any given loop is equal to the
magnitude of the voltage source.
Based on this definition, we shall apply
Kirchhoffs’ Voltage Law to the following loops:
WXBA: 6Volts =R1 I1 + R2I2
Substituting the Values of R1 and R2 we have:
6 Volts = I1 (5 Ω) + (20 Ω) I2 (4)
XYCB: 0 Volts= R3I3 + R4I4 - I2R2
Substituting the Values of R3 and R4 and R2:
0 Volts = I3 (5 Ω) + (15 Ω) I4 - (20 Ω )I2 (5)
Also remembering that : I3 = I1 – I2, and I4 =0.128
0 Volts = 5 Ω(I1 – I2 ) + 0.128(15 Ω) - (20 Ω )I2

7. Please note that the current I2 is in opposite
direction to the loop direction. This explains
the negative sign of the voltage drop as stated
in Equation (5).
Simplifying further, we have:
0 = 5I1 – 5I2 + 1.92 – 20I2
0 = 5I1 – 25I2 + 1.92
- 1.92 = 5I1 – 25I2 (5)
Solving Equation (5) and (4) by method of
elimination:
6 V = 5I1 + 20 I2 (4)
- 1.92 = 5I1 – 25I2 (5)
7.92 = 45I2 and I2 = 0.176 A

8. Substituting into any of the equations (5) or (4)
will give the value of I1 :
Solving Equation (5) and (4) by method of
elimination:
6 V = 5I1 + 20 (0.176 A) (4)
5I1 = 6 - 20 (0.176 A) and I1 = 0.496 A
We shall now attempt to confirm our answer by
substituting into (5):
- 1.92 = 5(0.496 A) – 25(0.176 A )
Method 2 : Alternatively, I1 and I2 can be
calculated by writing two equations based on
two unknowns from fig 2.

9. Loop WYCA :
6Volts = R1I1 + R3I3 + R4I4
Loop YZDC: 0 Volts = R5I5 – R4I4
I1 R1 I3 R 3 I5
W X Y Z
6V I2 R2 I4 R4 R5
A B C D
Fig 2
Substituting and simplifying, considering the
equations (1), (2) and (3)

10. I3 = I1 – I2 and I5 = I1 – I2 – 0.128
Loop WYCA :
6Volts = R1I1 + R3(I1 – I2 ) + R4(0.128 )
6Volts = (R1 + R3)I1 -R3 I2 + R4(0.128 )
6Volts = (5 + 5) Ω I1 - 5 Ω I2 + 15 Ω(0.128 )
6Volts = 10Ω I1 - 5 Ω I2 + 1.92
4.08Volts = 10Ω I1 - 5 Ω I2 (5)
Loop YZDC:
0 Volts = 10 Ω(I1 – I2 – 0.128 ) – (15 Ω ) (0.128 )
0Volts = 10 ΩI1 – 10 Ω I2 – 1.28 – 1.92
3.2Volts = 10 ΩI1 – 10 Ω I2 (6)
Equation (5) minus Equation (6):
0.88 Volts = (5 Ω) I2 therefore I2 = 0.176 A

11. Substituting this value of I2 = 0.176 A into
Equation (5)
4.08Volts = 10ΩI1 - 5 Ω (0.176A) (5)
I1 = 0.496 A
Method 3: A third method of evaluating I1 and I2
is based on the loop equations of figure 3.
Loop XYZDCB :
0 Volts = - I2R2 + I3R3 + I5R5
Voltage drop I2R2 is in the opposite direction to
direction of the loop
Loop WXYZDCBA:
6V = I1R1 + I3R3 + I5R5

12. Simplifying further:
I3 = I1 – I2 and I5 = I1 – I2 – 0.128
0 Volts = - I2R2 + I3R3 + I5R5
I1 R1 I3 R 3 I5
W X Y Z
6V I2 R2 I4 R4 R5
A B C D
Fig 3
0 Volts = - I2R2 + I(I1 – I2 )R3 + (I1 – I2 – 0.128 )R5
0 Volts = - I2 + I(I1 – I2 )R3 + (I1 – I2 – 0.128 )R5

13. 0 = -(20Ω)I2 + (I1 – I2 )(5 Ω ) +(I1 – I2 – 0.128 (10 Ω )
0 Volts = - 20I2 + 5I1 – 5I2 + 10I1 – 10 I2 – 1.28
0 Volts = - 35I2 + 15I1 – 1.28 (7)
1.28= - 35I2 + 15I1 (7)
6V = I1R1 + (I1 – I2 )R3 + (I1 – I2 – 0.128 )R5
6V = 5I1 + 5(I1 – I2 ) + 10(I1 – I2 – 0.128 )
6V = 5I1 + 5I1 – 5I2 + 10I1 – 10I2 – 1.28
6V = 20I1 – 15I2 – 1.28
(6+1.28)V = 20I1 – 15I2
7.28V = 20I1 – 15I2 (8)
Rearranging Equ (7): 1.28 = 15I1 - 35I2
Equation (7) X 2 and Equation (8) X 1.5

14. 2.56 = 30I1 - 70I2 (7) X 2
10.92 = 30I1 – 22.5I2 (8) X 1.5
(2.56 – 10.92) = - 70I2 + 22.5I2
I2= 0.176 A
Likewise, substituting I2 into
1.28= - 35I2 + 15I1
1.28= - 35(0.176 A ) + 15I1
I1= 0.496 A