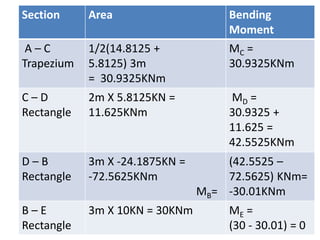
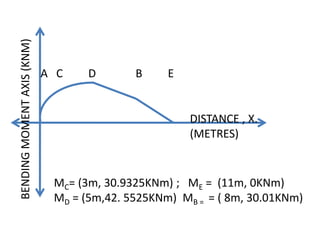
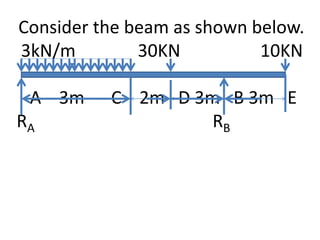
1) The document discusses shear force diagrams (SFD) and bending moment diagrams (BMD) for a loaded beam. 2) Key equations for a loaded beam include the sum of vertical forces equals zero, and the sum of clockwise and anticlockwise moments equals zero. 3) An example beam is given and the SFD and BMD are drawn by calculating reaction forces, shear forces, and bending moments at different points along the beam.

1. SHEAR FORCE DIAGRAMS &
BENDING MOMENT DIAGRAMS

2. Consider the beam as shown below.
3kN/m 30KN 10KN
A 3m C 2m D 3m B 3m E
RA RB

3. The two equations that govern a
loaded beam are:
a) Total vertical Forces Acting
Downward = Total Vertical forces
acting upward

4. b) Total Clockwise Moment About a
Turning Point = Total Anticlockwise
Moment about the same turning
point.

5. Based on the two equations above,
we are going to write two
equations.
a) Total Vertical Forces acting
downward =
(3KN/m X3m) + 30KN + 10KN

6. Total vertical forces acting upward=
RA + RB
The symbol for our equation a) is
usually written
ΣFV=0: 49KN = RA + RB (1)

7. The symbol for our equation b) is
usually written
ΣMA=0
This symbol means summation of
moments about the turning point
(support A) is zero.

8. The symbol for our equation b) is
usually written
ΣMA=0
This symbol means summation of
moments about the turning point
(support A) is zero.

9. The following diagram illustrates
clockwise and anticlockwise
moments about a support turning
point.

11. Based on the above diagram:
Let the weight of the boy on the left
hand side be A KN and the weight of
the boy on the right hand side be
B KN.
The weight of a body acts
downwards.

12. Anticlockwise moment:
AKilonewton exerts an
anticlockwise moment of A
Kilonewtons X x meters about the
support .
Assuming that the perpendicular
distance of the weight of A from the
turning point is x meters.

13. Clockwise moment:
BKN exerts an clockwise moment of
B Kilonewtons X w meters about the
support .
Assuming that the perpendicular
distance of the weight of B from the
turning point is w meters.

14. Based on the above definitions, we
are going to write an equation of
ΣMA=0 for the loaded beam.
Clockwise moments about RA
(3kN/m X 3m X (3/2)m) +
(30KN X 5m) + (10KN X 11m)
= 273.5KNm

15. (3kN/m X 3m X (3/2)m)
For the moment shown above:
3kN/m X 3m = magnitude of the
Uniformly distributed load.
(3/2)m represents the
perpendicular distance between the
turning point A and the point
through which the udl acts.

16. In order words, this moment is :
3 represents the span on which the
udl acts.
The magnitude of the udl , 3kN/m X
3m , acts through the middle of the
span.

17. (30KN X 5m)
This represents the moment of the
point load, 30KN, which acts at a
perpendicular distance of 5m from
the turning point, A.

18. For Anticlockwise moments:
RB X (3m + 2m + 3m)
RB represents the support reaction
acting vertically upwards.
(3m + 2m + 3m) represents the
distance between the support RB
and the turning point.

19. 273.5KNm = RB X (3m + 2m + 3m)
RB = 34.1875KN
From the equation RA + RB = 39
RA = (49 - 34.1875)KN = 14.8125KN

20. We shall now proceed to draw the
SFD.
Shear Force Diagram is a graph of
the vertical forces plotted on the y
axes and the horizontal
perpendicular distance of the force
on the x axis.
The point A is zero meters

21. C = 3m ; D = 5m etc
A C D B E
SHEARFORCEAXIS(KN)
DISTANCE , X. (METRES)

22. SFD KEY POINTS
1. The final vertical force at the
section E = 0
2. The sum of the upward vertical
forces = The sum of the downward
vertical forces as shown by the SFD.
3. ΣFV=0.

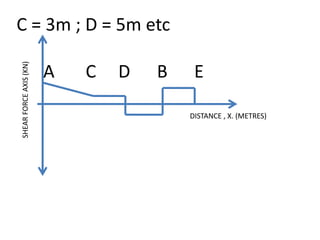
23. X ;Y coordinates Calculation
Point
A
Y= 14.8125KN;
X = 0 meters
Reaction
Support A
acts
Upwards
Point
C
Y = 5.8125KN
X = 3 m
14.8125KN
– (3KN/m
X 3m)]
Point
D
Y = 5.8125KN
X = 5m

24. X ;Y coordinates Calculation
D Y = -24.1875KN
X = 5m
(5.8125 -30 )KN
30KN acts
downward
B Y = -24.1875KN
X = 8 m
B Y = 10KN
X = 8 m
(34.1875 –
24.1875) KN
E Y;X = 10KN ; 11m
E Y = OKN
X = 11m
(10 -10)KN

26. BENDING MOMENT DIAGRAM
Bending Moment Diagram or Graph
is the graph of the bending moment
on the y axis plotted against the
distance, x metres, along the beam
(x axis).

27. BENDING MOMENT DIAGRAM
The values of the Bending moment
on the y axis can be evaluated by
calculating the areas under the
Shear Force diagram curve section
by section progressing from left to
right.

28. Section Area Bending
Moment
A – C
Trapezium
1/2(14.8125 +
5.8125) 3m
= 30.9325KNm
MC =
30.9325KNm
C – D
Rectangle
2m X 5.8125KN =
11.625KNm
MD =
30.9325 +
11.625 =
42.5525KNm
D – B
Rectangle
3m X -24.1875KN =
-72.5625KNm
MB=
(42.5525 –
72.5625) KNm=
-30.01KNm
B – E
Rectangle
3m X 10KN = 30KNm ME =
(30 - 30.01) = 0

29. BMD KEYPOINTS
1. The final bending moment at the
section E = 0
2. The total areas (+ve bending
moment) above the x axis =
The total areas (-ve bending
moment) below the x axis.
3. ΣMA=0

30. BENDINGMOMENTAXIS(KNM)
DISTANCE , X.
(METRES)
A C D B E
MC= (3m, 30.9325KNm) ; ME = (11m, 0KNm)
MD = (5m,42. 5525KNm) MB = = ( 8m, 30.01KNm)

31. BMD KEYPOINTS
4. The section of the Beam that
carries a uniformly distributed load
is represented as a curve on the
BMD.
5. The section of the Beam that
carries point loads are represented
by slant straight lines.