This document discusses multidimensional model order selection techniques. It begins by motivating the need for model order selection in applications such as analyzing stock market data, ultraviolet-visible spectrometry data, and sound source localization data. It then introduces tensor calculus and one-dimensional model order selection techniques before discussing novel contributions to multidimensional model order selection, including the R-D Exponential Fitting Test and Closed-Form PARAFAC based model order selection, which outperform existing techniques. Comparisons to other state-of-the-art methods are also discussed.

1. Multidimensional Model Order Selection
1

2. Motivation
Stock Markets: One example of [1]
⇒ Information: Long Term Government Bond interest rates.
Canada, USA, 6 European countries and Japan.
⇒ Result: by visual inspection of the Eigenvalues (EVD).
Three main components: Europe, Asia and North America.
[1]: M. Loteran, “Generating market risk scenarios using principal components analysis: methodological and
practical considerations”, in the Federal Reserve Board, March, 1997.
2

3. Motivation
Ultraviolet-visible (UV-vis) Spectrometry [2]
Wavelength
Oxidation state
pH
Radiation
Non-identified substance
samples
⇒ Result: successful application of tensor calculus.
In [2], the model order is estimated via the core consistency
analysis (CORCONDIA) by visual inspection.
[2]: K. S. Von Age, R. Bro, and P. Geladi, “Multi-way analysis with applications in the chemical sciences,”
Wiley, Aug. 2004.
3

4. Motivation
Sound source localization
Sound source 1
Sound source 2
Microphone array
⇒ Applications: interfaces between humans and robots and data
processing.
⇒ MOS: Corrected Frequency Exponential Fitting Test [3]
[3]: A. Quinlan and F. Asano, “Detection of overlapping speech in meeting recordings using the modified
exponential fitting test,” in Proc. 15th European Signal Processing Conference (EUSIPCO 2007),
Poznan, Poland.
4

5. Motivation
Wind tunnel evaluation
Array
W ind
Source: Carine El Kassis [4].
⇒ MOS: No technique is applied. [4]
[4]: C. El Kassis, “High-resolution parameter estimation schemes for non-uniform antenna arrays,” PhD
Thesis, SUPELEC, Universite Paris-Sud XI, 2009. (Wind tunnel photo provided by Renault)
5

6. Motivation
Channel model
Direction of Departure (DOD)
Transmit array: 1-D or 2-D
Direction of Arrival (DOA)
Receive array: 1-D or 2-D
Frequency Delay
Time Doppler shift
6

7. Motivation
An unlimited list of applications
⇒ Radar;
⇒ Sonar;
⇒ Communications;
⇒ Medical imaging;
⇒ Chemistry;
⇒ Food industry;
⇒ Pharmacy;
⇒ Psychometrics;
⇒ Reflection seismology;
⇒ EEG;
⇒…
7

8. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
8

9. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
9

10. Introduction
The model order selection (MOS)
⇒ is required for the principal component analysis (PCA).
⇒ is the amount of principal components of the data.
⇒ has several schemes based on the Eigenvalue Decomposition (EVD).
⇒ can be estimated via other properties of the data, e.g., removing
components until reaching the noise level or shift invariance property of
the data.
The multidimensional model order selection (R-D MOS)
⇒ requires a multidimensional structure of the data, which is taken into
account (this additional information is ignored by one dimensional MOS).
⇒ gives an improved performance compared to the MOS.
⇒ based on tensor calculus, e.g., instead of EVD and SVD, the Higher Order
Singular Value Decomposition (HOSVD) [5] is computed.
[5]: L. de Lathauwer, B. de Moor, and J. Vanderwalle, “A multilinear singular value decomposition”, SIAM J.
Matrix Anal. Appl., vol. 21(4), 2000.
10

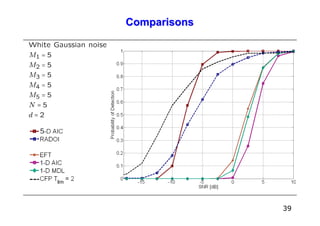
11. Introduction
A large number of model order selection (MOS) schemes have been proposed in
the literature. However,
⇒ most of the proposed MOS schemes are compared only to Akaike’s
Information Criterion (AIC) [6] and Minimum Description Length (MDL) [6];
⇒ the Probability of correct Detection (PoD) of these schemes is a function of
the array size (number of snapshots and number of sensors).
In [7], we have proposed expressions for the 1-D AIC and 1-D MDL. Moreover, for
matrix based data in the presence of white Gaussian noise, the Modified
Exponential Fitting Test (M-EFT)
⇒ outperforms 12 state-of-the-art matrix based model order selection
techniques for different array sizes.
For colored noise, the M-EFT is not suitable, as well as several other MOS
schemes, and the RADOI [8] reaches the best PoD according to our comparisons.
[6]: M. Wax and T. Kailath “Detection of signals by information theoretic criteria”, in IEEE Trans. on
Acoustics, Speech, and Signal Processing, vol. ASSP-33, pp. 387-392, 1974.
[7]: J. P. C. L. da Costa, A. Thakre, F. Roemer, and M. Haardt, “Comparison of model order selection
techniques for high-resolution parameter estimation algorithms,” in Proc. 54th International Scientific
Colloquium (IWK), (Ilmenau, Germany), Sept. 2009.
[8]: E. Radoi and A. Quinquis, “A new method for estimating the number of harmonic components in noise
with application in high resolution radar,” EURASIP Journal on Applied Signal Processing, 2004.
11

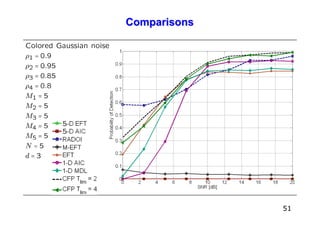
12. Introduction
One of the most well-known multidimensional model order selection schemes in the
literature is the Core Consistency Analysis (CORCONDIA) [9]
⇒ a subjective MOS scheme, i.e., depends on the visual interpretation.
In [10], we have proposed the Threshold-CORCONDIA (T-CORCONDIA)
⇒ which is non-subjective, and its PoD is close, but still inferior to the 1-D AIC and
1-D MDL.
By taking into account the multidimensional structure of the data, we extend the
M-EFT to the R-D EFT [10] for applications with white Gaussian noise.
For applications with colored noise, we proposed the Closed-Form PARAFAC
based Model Order Selection (CFP-MOS) scheme,
⇒ which outperforms the state-of-the-art colored noise scheme RADOI [11].
[9]: R. Bro and H.A.L. Kiers. A new efficient method for determining the number of components in
PARAFAC models. Journal of Chemometrics, 17:274–286,2003.
[10]: J. P. C. L. da Costa, M. Haardt, and F. Roemer, “Robust methods based on the HOSVD for estimating
the model order in PARAFAC models,” in Proc. 5-th IEEE Sensor Array and Multichannel Signal
Processing Workshop (SAM 2008), (Darmstadt, Germany), pp. 510 - 514, July 2008.
[11]: J. P. C. L. da Costa, F. Roemer, and M. Haardt, “Multidimensional model order via closed-form
PARAFAC for arbitrary noise correlations,” submitted to ITG Workshop on Smart Antennas 2010.
12

13. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
13

14. Tensor algebra
3-D tensor = 3-way array Unfoldings
“1-mode vectors”
M1
M3
M2 “2-mode vectors”
“3-mode vectors”
n-mode products between and
i.e., all the n-mode vectors
multiplied from the left-hand-side
by
1 2
14

15. The Higher-Order SVD (HOSVD)
Singular Value Decomposition Higher-Order SVD (Tucker3)
“Full SVD”
“Full HOSVD”
“Economy size SVD” “Economy size HOSVD”
Low-rank approximation (truncated HOSVD)
Low-rank approximation
Tensor data model
rank d
Matrix data model rank d
signal part noise part signal part noise part
15

16. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
16

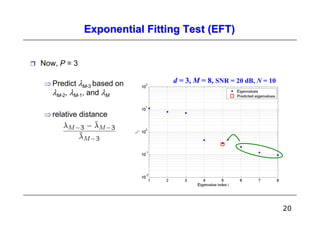
17. Exponential Fitting Test (EFT)
Observation is a superposition of noise and signal
⇒ The noise eigenvalues still exhibit the exponential profile [12,13]
⇒ We can predict the profile
of the noise eigenvalues
to find the “breaking point”
⇒ Let P denote the number
of candidate noise eigenvalues.
• choose the largest P
such that the P noise
eigenvalues can be fitted
with a decaying exponential
d = 3, M = 8, SNR = 20 dB, N = 10
[12]: J. Grouffaud, P. Larzabal, and H. Clergeot, “Some properties of ordered eigenvalues of a wishart
matrix: application in detection test and model order selection,” in Proceedings of the IEEE
International Conference on Acoustics, Speech and Signal Processing (ICASSP’96).
[13]: A. Quinlan, J.-P. Barbot, P. Larzabal, and M. Haardt, “Model order selection for short data: An
exponential fitting test (EFT),” EURASIP Journal on Applied Signal Processing, 2007
17

18. Exponential Fitting Test (EFT)
Start with P = 1
⇒ Predict λM-1 based on λM d = 3, M = 8, SNR = 20 dB, N = 10
⇒ Compare this prediction
with actual eigenvalue
⇒ relative distance:
⇒ In our case it agrees, we continue
18

19. Exponential Fitting Test (EFT)
Now, P = 2
⇒ Predict λM-2 based on d = 3, M = 8, SNR = 20 dB, N = 10
λM-1 and λM
⇒ relative distance
19

20. Exponential Fitting Test (EFT)
Now, P = 3
⇒ Predict λM-3 based on d = 3, M = 8, SNR = 20 dB, N = 10
λM-2, λM-1, and λM
⇒ relative distance
20

21. Exponential Fitting Test (EFT)
Now, P = 4
⇒ Predict λM-4 based on d = 3, M = 8, SNR = 20 dB, N = 10
λM-3, λM-2, λM-1, and λM
⇒ relative distance
21

22. Exponential Fitting Test (EFT)
Now, P = 5
⇒ Predict λM-5 based on d = 3, M = 8, SNR = 20 dB, N = 10
λM-4 , λM-3, λM-2, λM-1, and λM
⇒ relative distance
⇒ The relative distance
becomes very big, we have
found the break point.
22

23. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
23

24. R-D Exponential Fitting Test
r-mode eigenvalues
⇒ In the R-D case, we have a measurement tensor
⇒ This allows to define the r-mode sample covariance matrices
⇒ The eigenvalues of are denoted by for
⇒ They are related to the higher-order singular values of the
HOSVD of through
24

25. R-D Exponential Fitting Test
R-D exponential profile
⇒ The R-mode eigenvalues exhibit an exponential profile for every R
⇒ Assume . Then we can define global eigenvalues
⇒ The global eigenvalues also follow an exponential profile, since
⇒ The product across modes enhances the signal-to-noise ratio and
improves the fit to an exponential profile
25

26. R-D Exponential Fitting Test
R-D exponential profile
⇒ Comparison between the global eigenvalues profile and the profile
of the last unfolding
26

27. R-D Exponential Fitting Test
R-D EFT
⇒ Is an extended version of the M-EFT operating on the
⇒ Exploits the fact that the global eigenvalues still exhibit an exponential
profile
⇒ The enhanced SNR and the improved fit lead to significant
improvements in the performance
⇒ Is able to adapt to arrays of arbitrary size and dimension through the
adaptive definition of global eigenvalues
27

28. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
28

29. SVD and PARAFAC
Another way to look at the SVD
= + +
⇒ decomposition into a sum of rank one matrices
⇒ also referred to as principal components (PCA)
Tensor case:
= + +
29

30. HOSVD and PARAFAC
HOSVD PARAFAC
Core tensor Identity tensor
• Core tensor usually is full. R-D STE [14] • Identity tensor is always diagonal. CFP-PE [15]
[14]: M. Haardt, F. Roemer, and G. Del Galdo, ``Higher-order SVD based subspace estimation to improve
the parameter estimation accuracy in multi-dimensional harmonic retrieval problems,'' IEEE
Trans. Signal Processing, vol. 56, pp. 3198 - 3213, July 2008.
[15]: J. P. C. L. da Costa, F. Roemer, and M. Haardt, “Robust R-D parameter estimation via closed-form
PARAFAC,” submitted to ITG Workshop on Smart Antennas 2010.
30

31. Closed-form solution to PARAFAC
The task of PARAFAC analysis: Given (noisy) measurements
and the model order d, find
such that
Here is the higher-order Frobenius norm (sum of squared magnitude of all
elements).
Our approach: based on simultaneous matrix diagonalizations (“closed-form”).
By applying the closed-form PARAFAC (CFP) [16]
⇒ R*(R-1) simultaneous matrix diagonalizations (SMD) are possible;
⇒ R*(R-1) estimates for each factor are possible;
⇒ selection of the best solution by different heuristics (residuals of the SMD) is
done
[16]:F. Roemer and M. Haardt, “A closed-form solution for multilinear PARAFAC decompositions,” in
Proc. 5-th IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM 2008), (Darmstadt,
Germany), pp. 487 - 491, July 2008.
31

32. Closed-form PARAFAC based
Model Order Selection
For P = 2, i.e., P < d For P = 4, i.e., P > d
= + = + + +
= + = + + +
Assuming that d = 3, and solutions with the two smallest residuals of the SMD.
Using the same principle as in [17], the error is minimized when P = d.
Due to the permutation ambiguities, the components of different tensors are
ordered using the amplitude based approach proposed in [18].
[17]:J.-M. Papy, L. De Lathauwer, and S. Van Huffel, “A shift invariance-based order-selection technique for
exponential data modelling,” in IEEE Signal Processing Letters, vol. 14, No. 7, pp. 473 - 476, July 2007.
[18]:M. Weis, F. Roemer, M. Haardt, D. Jannek, and P. Husar, “Multi-dimensional Space-Time-Frequency
component analysis of event-related EEG data using closed-form PARAFAC,” in Proc. IEEE
Int. Conf. Acoust., Speech, and Signal Processing (ICASSP), (Taipei, Taiwan), pp. 349-352, Apr. 2009.
32

33. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
33

34. Comparisons
34

35. Comparisons
35

36. Comparisons
36

37. Comparisons
37

38. Comparisons
38

39. Comparisons
39

40. Comparisons
40

41. Comparisons
41

42. Comparisons
42

43. Comparisons
43

44. Comparisons
44

45. Comparisons
45

46. Comparisons
46

47. Comparisons
47

48. Comparisons
48

49. Comparisons
49

50. Comparisons
50

51. Comparisons
51

52. Outline
Motivation
Introduction
Tensor calculus
One dimensional Model Order Selection
⇒ Exponential Fitting Test
Multidimensional Model Order Selection (R-D MOS)
⇒ Novel contributions
• R-D Exponential Fitting Test (R-D EFT)
• Closed-form PARAFAC based model order selection (CFP-MOS)
Comparisons
Conclusions
52

53. Conclusions
State-of-the-art one dimensional and multidimensional model order selection
techniques were presented;
For one dimensional scenarios:
⇒ in the presence of white Gaussian noise
• Modified Exponential Fitting Test (M-EFT)
⇒ in the presence of severe colored Gaussian noise
• RADOI
For multidimensional scenarios:
⇒ in the presence of white Gaussian noise
• R-dimensional Exponential Fitting Test (R-D EFT)
⇒ in the presence of colored noise
• Closed-form PARAFAC based Model Order Selection (CFP-MOS)
scheme
The mentioned schemes are applicable to problems with a PARAFAC data
model, which are found in several scientific fields.
53

54. Thank you for your attention!
Vielen Dank für Ihre Aufmerksamkeit!
54